Folytatás a III. rész után.

A teljes megoldást az aszimptotikus függvény és az x változó polinomjának szorzata adja meg. Az egyenletben szereplő ε = m.e².r₀/ℏ²  mennyiség olyan értékét keressük, amikor a  polinom szorzata az aszimptotikus függvénnyel reguláris (tehát véges értékű) megoldást ad . Az itt nem közölt számítások szerint a megoldás ε = n egészszám lesz, amely legalább eggyel nagyobb az l impulzusmomentum kvantumszámnál, azaz n ≧ l+1. Az n kvantumszám határozza meg a karakterisztikus sugarat  r₀ = a₀.n, ahol a₀ = ℏ²/(m.e²) az un. Bohr sugár, amit az energia kifejezésébe helyettesítve azonos eredményt kapunk, mint amit Bohr klasszikus úton levezetett.

A Schrödinger-egyenlet tehát azonos eredményre vezet, mint Bohr körpályás modellje, amikor az energiáról van szó, de alapvetően eltér az impulzusmomentum és az energia kapcsolata: ugyanakkora E_n energiához különböző nagyságú pálya-impulzusmomentumok tartozhatnak, melyek értéke mindig kisebb, mint n.ℏ  és a nulla is megengedett. Ez egyébként a kvantummechanikai megfelelője annak a klasszikus fizikai törvénynek, hogy centrális térben a bolygók különböző elliptikus pályákon mozoghatnak azonos energia esetén is. A Bohr modellben tiltott nulla impulzusmomentumú pályák fellépése azt jelenti, hogy az elektron áthaladhat az atommagon. Ez szintén megengedett bolygómozgás esetén, de ekkor a bolygó megsemmisül, szemben az elektronnal, amelyik nem lép olyan kölcsönhatásba az atommaggal, amely megakadályozná az elektron centrumon való áthaladását. Az elektron kinetikus energiájához ezért kétféle mozgás ad járulékot, az egyik a sugár koordináta (oszcilláció), a másik a szög koordináták terében (keringés) halad. Az n = 1 fő kvantumszámmal jellemzett pályán l = 0, tehát alapállapotban nincs is keringő mozgás, ekkor csak oszcillációs jellegű mozgásról beszélhetünk, azaz a pálya áthalad az atommagon. A kvantummechanika nyelvén ez azt jelenti, hogy az l = 0 állapotok (un. „s” pályák) sűrűsége nem nulla a centrumban.  Az ehhez tartozó energia E₁ = – ½m.e⁴/ℏ² =  – ½e²/a_₀ párhuzamba hozható az oszcillátorok zérusponti energiájával, de ennek értéke negatív szemben az oszcillátorok pozitív energiaskálájával. Ennek oka, hogy a molekulavibrációknál nem vettük figyelembe az atomok közötti negatív kötési energiát, és az energia nulla pontját a rezgésmentes állapothoz rögzítettük, ahol a potenciális energiának minimuma van. 

A klasszikus bolygómozgással szemben, ahol minden pillanatban meg tudjuk mondani a tartózkodási helyet, a sebességet és a gyorsulást, a kvantummechanika csak a tartózkodási valószínűséget valamint a sebesség és a gyorsulás várhatóértékét adja meg az állapotfüggvény segítségével. Az n és l  kvantumszámokhoz tartozó függvényeket a P^l_n(x) Laguerre polinomok építik fel. A hullámfüggvény alakja:

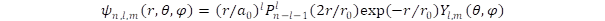
A Laguerre polinom foka n–l–1, amelynek maximális értéke n–1. Az origóban, azaz a mag helyén élesen elkülönül az l = 0 (ezeket hívjuk s pályáknak) és az l > 0 (p, d, f …) pályák térszerkezete. Az előbbi a magban nullától különböző sűrűséggel rendelkezik, mert a Laguerre polinom értéke nem nulla az origóban, míg az utóbbi esetben az r^l tényező miatt az állapotfüggvény itt zérus lesz. Ez megfelel az impulzusmomentum definíciójának, hiszen ha véges valószínűséggel tartózkodna az elektron a magban, akkor csak nulla lehetne az impulzusmomentum, míg ha van impulzusmomentum, akkor nem tartózkodhat az objektum a forgás középpontjában.  

Az n és l kvantumszámú „nl” pályák térbeli eloszlását a Laguerre polinomok határozzák meg. Az oszcilláció egy-dimenziós mozgásával ellentétben az elektron háromdimenziós térben mozog az atommag környezetében, ezért annak valószínűségét, hogy az s elektron a magtól valamilyen r távolságban tartózkodik, úgy számítjuk ki, hogy szorozzuk a valószínűségsűrűséget a gömb 4r².π felszínével. Az ennek megfelelő valószínűség eloszlást a mutatja az ábra:

Az 1s (piros), 2s (fekete) és 3s (kék) pályák valószínűség eloszlása Bohr sugár egységben 

Az 1s pálya (n = 1, l = 0) eloszlási valószínűségének egy maximuma van hasonlóan a harmonikus oszcilláció n = 0 alapállapotához, a maximumok száma tekintetében azonosság van a 2s pálya (n = 2, l = 0)  és az oszcilláció n = 2 módusa, illetve a 3s pálya (n = 3, l = 0) és az oszcilláció n = 4 módusa között. Szintén hasonlóság van a harmonikus oszcillációval abban a tekintetben, hogy ott is a külső módus amplitúdója a legnagyobb. Az  ábrán látható, hogy a külső módusok távolsága a fő kvantumszám négyzetével arányosan növekszik és egyre diffúzabbá válik. Ezek a tulajdonságok avval függnek össze, hogy a vonzóerő kis távolságokban veszi fel a nagyobb értéket és csökken az atommagtól távolodva. 

Az eloszlási maximumok száma a fő kvantumszámmal egyezik meg, a csomópontok száma (nulla helyeké) n – 1 lesz, a megtalálási valószínűség nulla a centrumban, és a több módusú eloszlásokban az elektron a külső tartományban tartózkodik a legnagyobb valószínűséggel. Nagy n kvantumszámoknál a belső módusok súlya erősen lecsökken, hasonlóan az oszcillációk esetével. A nullától különböző l értékkel rendelkező pályák közül az l = n–1 pálya radiális függvénye könnyen megadható, mert ekkor a Laguerre polinom nullafokú. Az állapotfüggvény:

A radiális függvény négyzete adja meg az elektron valószínűségsűrűségét egy adott távolságban, amit az n = 2, l = 1 (2p pálya), n = 3, l = 2 (3d pálya) és n = 4, l = 3 (4f pálya) esetén mutat meg a következő ábra

Az 2p (piros), 3d (fekete) és 4f (kék) pályák valószínűségsűrűsége Bohr sugár egységben

Folytatás az V. részben: : "Miért diszkrétek az energianívók kötött állapotban_V"

További bejegyzések összefoglalója: "Paradigmaváltás a fizikában"