The origin of covariance in the special relativity
Antal Rockenbauer
Institute of Materials and Environmental Chemistry, Hungarian Academy of Sciences;
Department of Physics, Budapest University of Technology and Economics
DOI: 10.13140/RG.2.1.2441.1366
Abstract
The covariance rule of special relativity can be derived from the E = p.c relation of elementary particles if this relation is valid not only for the photons but also for any particles having rest mass. This extension assumes intrinsic motion at a speed of light producing the rest mass as a consequence of singularity in the Lorentz transformation. The fermions are constructed by two-dimensional rotation with right or left-handed chirality, and the chirality is manifested in the duality of particles and antiparticles. Due to the double rotation the spin of fermions is less by a factor two with respect to the photons defined by single rotation. Parity violation in the beta decay is explained that the customary inversion is limited to the external motion without the intrinsic motion of particles, where the latter transformation represents the charge conjugation. Though the speed and momentum are non-observable in stationary state, the intrinsic motions can be regarded as real physical motion, since the momentum can be derived from the rest energy and intrinsic angular momentum of particles.
PACS: 03.65.Pm: 03.65.Vf
Corresponding author, e-mail: rockenbauer.antal@ttk.mta.hu
1. Introduction
In the theory of special relativity the transformation rules are expressed by covariance of four dimensional vectors in the spacetime [1-2]. The square of components is summed producing invariants independent from the choice of inertial systems. The equation of motion is expressed by the four dimensional momentum-energy vector (px, py, pz, iE/c), in which the length of this vector is proportional to the rest mass, which manifests the covariance. If the rest mass is zero, like in the case of photons, the invariance gives proportionality between the energy and the momentum as E = p.c [3]. In this paper we raise the question whether this relationship can be extended for massive particles by assuming intrinsic rotation as a source of the rest energy [4]. This assumption extends also the total momentum of particles by a contribution from the intrinsic rotation. We discuss also the role of spherical symmetry in the relativistic laws, the role of chirality for explaining the duality of particles and antiparticles and raise the question of why the elementary particles have the same spin even though their rest mass can be very different.
The role of extended inversion symmetry will be discussed, when this symmetry involves also reflection in the space of intrinsic motion. The aim of this analysis is to find the symmetry reason of parity violation [5]. Finally a question is raised of whether it has any physical sense of speaking about intrinsic rotation in the time independent stationary state.
- Theory
2.1. The singularity of Lorentz transformation
The theory of special relativity is based on the Lorentz transformation, which defines the length of the 4-dimensional space-time vector (x,y,z, ict) as a covariant, that is the relation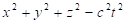 
is independent on the choice of inertial frame moving at constant speed [1-2]. A further covariant of the theory is the length of momentum-energy vector (px, py, pz, iE/c), which defines the rest mass by the relation: 
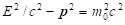. The energy can be expressed from this relation (1)::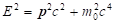
The different energy terms (kinetic, potential, electromagnetic) are added together linearly, the same holds for the energy of particles in atoms and molecules. The energy is defined by the operator 
in the Schroedinger representation, where the linearity of time produces also linear addition rule, thus Eq. (1) can be considered as an exception of the general rule. The question can be raised of why in the special relativity the square of the energy terms is added up? Such relation is expected for orthogonal vectors, namely if the rest energy is produced by an intrinsic momentum and its expectation value is zero <p0> = 0. In this case the total momentum of particles contains an external p1 and intrinsic p0 components:
p = p1 + p0 (2)
The expectation value for the square of total momentum is 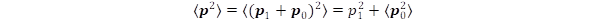(3):
(3)
In Eq. (3) the <p0> = 0 condition was applied. The E = p.c relation becomes equivalent to the energy formula of special relativity if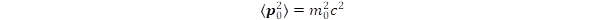 
.
This relation means that the m0 mass should rotate with the speed of light. In this case, however, not the already existing m0 is accelerated to the speed of light, since then the mass would be infinite, but the zero mass of a rotating space point will create the m0 mass by the infinitely large relativistic increase. We can use this assumption to define the mass of space points having zero limiting value (4):
(4)
In our analysis we attribute great importance for the singularity of relativistic rules when the physical objects move with the speed of light, since it can offer a clue of how the space with zero mass can create finite mass. As an example we refer to the case of photons with zero rest mass, where due to the equivalence between mass and energy, the photon should have also mass m = ℏω/c2. This mass, however, is not considered as rest mass, since the photons can never be “in rest”, but it moves with the speed c. Thus we can speak about motional mass, which can be created by the product of an infinitely large factor due to the singularity and a zero mass. In this context the zero mass of space points is considered as a limiting value defined by Eq. (4). Similarly to the photons, we assume the same mass formation mechanism for all elementary particles where their intrinsic motion has the speed of light. The difference between photons and fermions is manifested in the localization: in the case of fermions the intrinsic motion is localized in the space, why no defined position can be rendered to the propagating photons.
- Results
3.1. The origin of spin
Let us define the p0 amplitude of momentum from the equality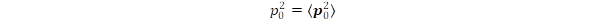 
then we obtain p0 = m0.c. Furthermore, the condition <p0> = 0 can be fulfilled if the intrinsic motion is manifested by rotations. Denote by ω0 the frequency of rotation then the radius is r0 = c/ω0, since the peripheral speed is c. The z component of angular momentum can be given as Lz = r0.p0 = m0c2/ω0. This relation follows from the fact, that the singularity criterion is fulfilled only at the radius r0, thus the entire mass and momentum are concentrated at this distance from the center of rotation.
We postulate all particles including the photons as stationary state of the spacetime created by intrinsic rotation with the speed of light. The dimension of particles is finite around the rotational axes, since at the radius r0 = c/ω0 the peripheral speed reaches c. The photons can both rotate and propagate along the rotational axes. Since for photons the angular momentum is Lz = ±ℏ, we obtain that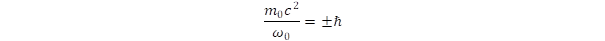 
where the sign of ω0 shows the polarization of light. The sign of mass can be conventionally chosen positive, but in principle both signs are allowed, since the relativistic relation contains the square of momentum. The relation for angular momentum can be rewritten to express energy: m0c2 = ℏ.ω0, that is, the frequency of intrinsic rotation is equal to the customary frequency of photons. According to quantum theory, the angular momentum of an orbiting object can have eigenvalues of the integer multiple of ℏ Planck constant [6], which criterion is fulfilled by the photons. For fermions, however, where the spin S = ½ is half integer, the same rotational model cannot be applied. In order to find the proper model, we start from the symmetry of fermions, which is evidently spherical and can be realized by motions covering all points on the surface of a sphere. This requirement can be fulfilled if the axis of primary rotation is also rotating around a second perpendicular axis. We name this type of motion as double rotation. This rotational model also explains why the rest mass is zero for photons and non-zero for fermions. The single rotation defines only an axis, while the double rotation determines a well-defined point in the space, consequently, the former motion cannot localize the mass, only the latter can do it.
According to the quantum mechanical rules of angular momentum <S2> = S(S+1), furthermore the isotropic character of double rotation allows only S = ½ spin, since except the zero spin, only the spin S=½ fulfills the requirement of isotropy. The isotropy is expressed in the definition of Dirac spinors [7-8] by giving identical expectation values for the square of spin components: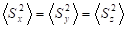 
; which leads to the equation: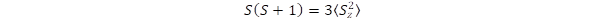(5):
(5)
This relation can be fulfilled by the spin ½.
The group theory also supports the assignment of S = ½ spin to double rotation. In this case the standard rotation-inversion group should be extended by a new element having a rotational angle 2π. This rotation is no more a unit element of the symmetry group, since the other rotation around a second axis is also necessary for transforming the object to identical orientation. The existence of this special symmetry element can also be explained by the requirement that the double rotation should cover the 4π surface of a sphere of unit radius instead of the 2π angle of the circle. This rotation of an angle 2π was suggested originally by Bethe [9], who introduced the concept of double groups, which group – beside the odd dimensional representations – also has two-dimensional irreducible representations, which can be assigned to the spin S = ½.
Classical physics can also rationalize why the double rotation reduces by a factor 2 the angular momentum with respect to a single rotation. The first rotation can produce a circular orbit and the second rotation will turn this circle around its diameter. The moment of inertia is smaller by a factor 2 in the latter case, which results in a spin S = ½ since the angular and inertial moments are proportional.
A further question can be raised of why the spin is independent of the mass of particles? According to the standard model [10] all interaction mediating bosons have the spin S = 1 [11], and all elementary fermions have the spin S = ½ irrespectivly of the rest mass. This fact is a trivial consequence of rotation if the peripheral speed is c, since then the radius of rotation is c/ω, while the mass is proportional to the ω frequency, and thus the angular momentum, which is expressed by their product, should be independent of the frequency and consequently of the mass.
We can also approach the question on the basis of rotational equilibrium between centripetal and centrifugal forces. The intrinsic rotation produces centrifugal force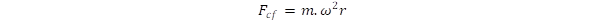 
due to the inertia. For photons the centrifugal force can be rewritten by substituting m = ℏ.ω/c2 and r = c/ω, which gives
. As we pointed out in a previous publication [4], this force is balanced by the strong gravitation
caused by the extreme curvature of space, when the rotation has the speed of light. It means that the intrinsic rotation of photons is a self-supporting motion in the space. In the case of double rotations defining the fermions, the strong gravitation has to balance a centrifugal force produced by two different rotations, that is: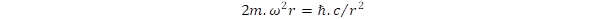 
.
From this relation, we can derive the angular momentum Lz = m.c.r = ℏ/2, which shows again that the concept of double rotation results in the spin S = ½.
3.2. The chirality of double rotation and the parity violation
The double rotation has the symmetry of chirality, since the sense of second rotation can be either right- or left-handed, and for this reason two types of fermions exist: the particles and antiparticles. The inversion symmetry transforms not only the external coordinates, but also the intrinsic space, which means the total symmetry operation transforms the particles into antiparticles, since the left-handed chirality is reflected into the right-handed one. This fact offers a straightforward explanation why the parity symmetry is violated in the beta decay of neutron [5]. The customary parity is defined in the external space and does not reflect the intrinsic motions, that is, the charge conjugation transforming the particles into antiparticle is not included in this operation. The complete inversion, however, should also reflect the intrinsic motions, thus it contains both the parity and charge conjugation. It is in accordance with the experimental observations finding symmetry only when the parity and charge conjugation is combined called as the PC symmetry.
3.3. The physical sense of intrinsic rotation
The question can be raised of whether the intrinsic rotation, which can explain the origin of spin, mass and charge of the elementary particles, could be considered as a real physical motion? In classical physics, the orbits of rotating objects can be described by the r(t), u(t) and p(t) functions of position, speed and momentum, which functions cannot be defined for the stationary states of quantum mechanics. This fact comes from the structure of stationary wavefunction, which are the products of a purely time- and a purely space dependent components if in the Schrodinger or Dirac equation [6], the potential energy has no time dependence. In this state we cannot speak about speed or acceleration, since any physical parameter as well as the probability distribution become independent of time. Furthermore, we cannot speak about momentum outside the center, since its spatial distribution Ψ(r)pΨ(r) is imaginary at every space point except the center, where this is zero. The expectation value of momentum is also zero. We can, however, attribute momentum for the intrinsic rotation if we calculate the distribution of its square Ψ(r)p2Ψ(r), which is real and proportional to the local kinetic energy in the non-relativistic approach, or to the square of energy in the case of relativistic singularity. The intrinsic rotation belongs to the latter case, where from the expectation value of <p2> , we can derive the amplitude of momentum as p0 = m0.c.
The apparent conflict in the interpretation of momentum is related to the concept of stationary state. In order to measure the speed, we have to determine the position at two different times, but the first measurement changes the original stationary state, so the second measurement cannot tell any information about the original state. Thus in stationary state the speed and consequently the momentum escape observation. The non-observable character of momentum is expressed in quantum mechanics that the momentum becomes imaginary. It does not mean, however, that no momentum exists. The existence of momentum is evidenced by the kinetic (rest) energy and intrinsic spin of particles. Since all characteristic physical quantities of motion exist, we can claim that the intrinsic rotation represents a real physical motion. Due to the singularity of Lorentz contraction: s when u = c, the perimeter of a circle, or the surface of a sphere become zero for single or double rotation, respectively. The radius of rotation, however, is not reduced, since this is perpendicular to the motion. This concept is well supported by the electron-positron or Bhabha scattering experiments [12], which can offer information for the area of electron surface. This type of scattering may reveal if the finite charge distribution of an electron can modify the differential cross-section [13]. The main conclusion from the LEP1 and LEP2 experiments at CERN (100 GeV region) was that the low-angle scattering data agree with the results of theoretical calculations based on quantum electrodynamics to very high accuracy. It means that any radius computed from the electron surface should be less than the Compton wavelength by 5 orders of magnitude. This result is in agreement with the concept of intrinsic rotation at the speed of light rendering zero surface for the electrons.
- Conclusion
The spacetime and elementary particles constitute our physical world together and their role is interdependent: On the one hand, the intrinsic motion of space creates the particles, on the other hand, the proportionality of energy and momentum of particles build up the basic transformation rules of the spacetime.
The covariances of special relativity are based on the assumption that for any particles the energy is proportional to the total momentum, which includes also a contribution from the intrinsic rotation. The mass and angular momentum of particles are created by motions with the speed of light, for photons a single rotation is combined with the propagation yielding the spin S = 1, for fermions a double rotation can produce S = ½ spin. This assignment is based on both classical physical, quantum mechanical and group theoretical arguments. The rest mass of fermions and motional mass of photons are interpreted by the local or non-local nature of intrinsic motion, respectively.
The left and right handed chirality of double rotations represent the particles and antiparticles, respectively. The parity violation in beta decay is due to the incomplete definition of inversion affecting only the external motion without taking into account the intrinsic rotation. The extension of this symmetry into the space of intrinsic rotation leads to the CP symmetry.
Though in quantum mechanics the speed and momentum of particles are not observables in stationary states, these physical quantities can be derived from the rest energy and intrinsic angular momentum, which justifies the physical reality of the intrinsic rotation of particles.
Additional topics in the blog, see: "Paradgmaváltás a fizikában."
References
[1] H A Lorentz, Proc. Acad. Science Amsterdam I, 427 (1899)
[2] W Rindler, Essential Relativity. (Birkhäuser), (1977)
[3] R P Feynman, R B Leighton and M Sands The Feynman Lectures on Physics (Addison-Wesley Publishing, Massachusetts) Vol. 2, (1964)
[4] A Rockenbauer Indian J. Phys. 89, 389-396 (2015)
[5] T D Lee and C N Yang Phys. Rev. 104 822 (1956)
[6] A Messiah Quantum Mechanics (North-Holland, Amsterdam) Vol. I,II (1962)
[7] P A M Dirac Proc. Roy. Soc. A117 610 (1928)
[8] L Foldy and S A Wouthuysen Phys. Rev. 78 29 (1950)
[9] H Bethe Ann. Physik 395 133 (1929)
[10] D J Griffith Introduction to Elementary Particles (John Wiley et Sons: New York) (1987)
[11] The W and Z bosons of weak interaction can be represented by a similar rotation-propagation model as suggested for the photons, but in this case the direction of propagation is perpendicular to the axis of rotation, which induces Coriolis force and consequently electric charge. The propagation increases the self radius of particles and reduces their frequency and rest mass making the bosons short lived and localized in space. As a consequence, the bosons posses rest mass and mediate weak interaction in a short distance.
[12] H J Bhabha Proc. Roy. Soc. A154 195 (1936)
[13] A Arbuzov, M Bigi, H Burkhardt et al. Phys. Lett. B. 383 238 (1996)
