Az atom klasszikus Bohr modellje
Az előző részben tettük fel a kérdést, hogy a kvantummechanikai oszcillátorok energiája miért rendelkezik diszkrét értékekkel. Mivel a diszkrét energiaértékek megjelenése a kvantummechanika általános tulajdonsága, ezért ezt célszerű megvizsgálni más kötött rendszereket is, amit e-helyen a centrális erőtérben mozgó elektron esetével illusztrálunk. Az oszcillátoroknál olyan mozgásokat vizsgáltunk, ahol az erőnek kitüntetett iránya van és az erő nagysága arányos a kitéréssel. Ebben a részben gömbszimmetrikus potenciáltérrel dolgozunk, amelyik éppen fordítva változik a távolsággal: az erő nagysága a távolság négyzetével csökken
F = – k/r2, ekkor a potenciál V = –k/r
Ilyen típusú erő a gravitáció, ahol az erőállandó k = γ.m.M (itt γ a gravitációs állandó, m és M a két tömeg) és a Coulomb-kölcsönhatás, ahol k = q.Q (itt q és Q az elektromos töltés). Azt az esetet vizsgáljuk, amikor a kölcsönható objektumok egyikének tömege sokkal nagyobb, mint a másiké. Ez felel meg a Nap körül keringő bolygók esetének, illetve az elektronok mozgásának az atommag körül. A klasszikus fizikában a Newton-egyenletből indulunk ki:
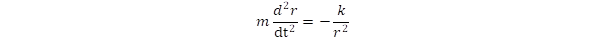
Itt az r(t) vektor mutatja a kis tömegű objektum pillanatnyi pozícióját a mozdulatlannak feltételezett nagy tömegű objektumhoz képest és r az r vektor hosszúsága. Az egyenlet általános megoldása ellipszis pályákat eredményez, ennek speciális esetét vizsgáljuk, amikor a pálya szabályos kör. Ekkor a gyorsulás d2r/dt2 = –ω2.r, a kerületi sebesség dr/dt = ω.r lesz, ahol ω a forgás körfrekvenciája. Ily módon jutunk el Kepler második törvényéhez
m.ω2.r = k/r2 azaz ω2r3 = k/M = konstans
Az egyenlet annyiban emlékeztet a rezgőmozgás esetére, hogy ebben az esetben is a frekvencia négyzete arányos az erőállandó és a tömeg hányadosával, de szemben az oszcillációval, ahol nem függött a frekvencia a rezgési amplitúdótól, itt a keringési sugár növekedése csökkenti a frekvenciát. A körmozgás sajátossága, hogy egyaránt állandó a kinetikus energia és a potenciális energia, szemben az oszcillációval, ahol az energia megmaradás azáltal valósul meg, hogy a kinetikus és potenciális energia egymásba alakul át a mozgás során. Körmozgásnál a teljes energia a potenciális energia fele és abszolút értékben megegyezik a kinetikus energiával:
E = – ½m. ω2.r2 = – ½γ.m.M/r
Az energiát kifejezhetjük az L = m.ω.r2 impulzusmomentum segítségével is, amit átrendezve ω.r = k/L és így
E = – ½m.k2/L2
Centrális erőtérben a körforgást végző objektum energiája az impulzusmomentum négyzetével fordítottan arányos. A klasszikus fizika felfogása szerint az impulzusmomentum folytonosan változtatható, ennek megfelelően változik az energia és a sugár is. Ezzel szemben centrális erőtérben mozgó elektronok energiája kvantumokban változik, mert az állapotok közötti átmenetet fotonok hozzák létre és ennek során ℏ impulzusmomentum átadására kerül sor, ez okozza, hogy az elektron pálya-impulzusmomentuma csak ℏ egész számú többszöröse lehet. Ezt fejezi ki a Bohr által megállapított kvantumfeltétel, mely szerint stacionárius állapotban L = n. ℏ, ahol n egész szám. Ezt behelyettesítve a hidrogénatom energia kifejezésébe kapjuk, hogy
En = – ½m.e4/(n.ℏ)2
Itt az erőállandó k = e2, mert a proton és elektron egyaránt az e elemi töltéssel rendelkezik. Az n → n+1 kvantumátmenethez tartozó fotonok frekvenciája
ω(n+1→n) = (En+1 – En)/ ℏ
pontosan megfelel a hidrogénatom színképében megfigyelt vonalaknak. Felfogásunk szerint a korábban tárgyalt oszcillátorokhoz hasonlóan az elektron energiaállapotai is azért diszkrétek, mert a fotonok csak jól meghatározott energiakülönbségeket tudnak gerjeszteni. Egy hasonlattal élve: ha egy hordót feltöltünk vízzel, akkor a víz felső szintje tetszőleges lehet. De ha mindig tele vödörrel adagoljuk a vizet, akkor csak diszkrét szintmagasságok jönnek létre. Oszcillátorokban azért csak diszkrét energiájú fotonok változtatják meg az energiát, mert az átmenetek rezonanciaszerűen mennek végbe a rezgés sajátfrekvenciáján, a foton frekvenciája pedig meghatározza az energiáját, ugyanakkor a centrális térben mozgó elektronoknál a kölcsönható foton ℏ impulzusmomentuma választja ki azokat az energianívókat, amelyek között átmenet indukálható. Az adagokban érkező, vagy elvitt impulzusmomentum viszont kijelöli azokat az energiaszinteket, amit az atommag körül mozgó elektron felvehet.
Szemléltessük egy hasonlattal, hogyan is megy végbe a folyamat. Képzeljük el, hogy űrhajóval közeledünk egy bolygóhoz és keresünk egy keringési pályát. Ennek érdekében egymásután rakétákat lövünk ki, amelyik fokozatosan változtatja meg az űrhajó pályáját. Ehhez hasonlíthatjuk a proton felé közeledő elektron esetét. A töltések közötti vonzóerő hatására megváltozik az elektron sebessége, a sebesség változása viszont elektromágneses sugárzás, azaz foton kibocsátással jár együtt. De bármekkora is legyen a foton energiája, minden egyes foton elvisz, vagy hoz ħ egységnyi impulzusmomentumot, emiatt a gyorsulás, vagy lassulást nem folytonosan, hanem kvantumokban történik, hasonlóan az űrhajóhoz, ahol a rakéták révén szakaszosan történik a pályamódosítás. Amikor végül az elektron kötött állapotba kerül, impulzusmomentuma csak ħ egészszámú többszöröse lehet.
A kötött elektron és a fotonok külön-külön folytonosan változó energiaszintekkel rendelkeznek, de a foton abszorpció és emisszió kiválasztási szabályai miatt már csak diszkrét értékekkel változhat meg az elektronok energiája. Tehát diszkrét vonalak megjelenése az atomok és molekulák spektrumában azt mutatja, hogy a vizsgált rendszer valamilyen kiválasztási szabály szerint változtatja meg az energiáját a fotonokkal való kölcsönhatás során. Nem minden esetben van azonban ilyen határozott kiválasztási szabály, példa rá a nem kötött állapotban lévő elektronok mozgása. Ebben az esetben már a kvantummechanika formalizmus is folytonosan változó energiaállapotokat ad meg. A kvantummechanika eredeti megfogalmazása csak az atomi rendszerek, mindenekelőtt az elektron energia operátorát veszi figyelembe a fotonokkal való kölcsönhatás nélkül, de így is kitűnő leírást ad az energia átmenetek törvényeiről. Ez arra utal, hogy a Planck állandóval „skálázott” operátor formalizmus összhangban van a fotonok és az elektronok kölcsönhatási mechanizmusával. Ugyanakkor az eljárás korlátait mutatja, hogy még relativisztikus kiterjesztés esetén (Dirac egyenlet) sem tud számot adni bizonyos jelenségekről, így például az elektron anomális mágneses momentumáról. Erre csak a kvantumelektrodinamika képes a második kvantálás bevezetésével, amikor a fotonok és elektronok kölcsönhatását egységes keretek között tárgyalja az elmélet.
Bohr, amikor kimondta az impulzusmomentumra vonatkozó kvantumfeltételt, a jelenség lényegi vonatkozását találta meg. Ennek köszönhető, hogy sikeresen lehetett értelmezni a hidrogénatom színképét. Az elv azonban már nem bizonyult elegendőnek olyan atomok esetén, ahol nem csak egyetlen elektron kering a mag körül. A kvantummechanika oldaláról tekintve tulajdonképp az a meglepő, hogy a hidrogén atom esetén olyan sikeres volt a modell. A modell alapvető korlátja, hogy körpályán helyezi el az elektronokat, noha ez csak egy rendkívül speciális esete a mozgásnak, hiszen a bolygók is elliptikus pályán keringenek, ahol a körpályától való eltérést az excentricitás (a két tengely aránya) jellemzi. Pontos körpálya akkor alakul ki, ha az indító impulzus éppen merőleges a sugárirányra, de amikor ez a feltétel nem teljesül már ellipszis pálya jön létre. Az elliptikus pálya másik határesete, amikor az impulzus párhuzamos a kitéréssel, voltaképp ez már rezgő mozgás, amivel az oszcillátoroknál foglalkoztunk. Bolygómozgásnál azért nem jön létre oszcilláció, mert ekkor a bolygó már beleesik a napba és megsemmisül. Mi az eset az elektronokkal, azt várnánk, hogy megsemmisülnek, ha az atommaggal ütköznek, hiszen pontszerű objektumokat feltételezve ekkor végtelen nagy vonzóerő egyesítené az atommagot és az elektront. A körpályára alapított modellben ez a probléma nem merül fel, mert ha az impulzusmomentum nem nulla, akkor a kör sugara véges, tehát véges marad a potenciális energia is. A véges impulzusmomentum a Bohr modellben azt jelenti, hogy a kvantumszám legkisebb értéke egy és nem pedig nulla. Ha ugyanis n = 0 lenne, akkor az energia végtelen negatív értéket venne fel. A Bohr modellnek az a megkötése, hogy a n kvantumszám egyúttal meghatározza az elektron n.ℏ impulzusmomentumát is, már nem bizonyult helytállónak. A kvantumelmélet szerint az n kvantumszámú állapotban a maximális impulzusmomentum (n–1).ℏ, így például, amikor n = 1, csak nulla lehet az impulzusmomentum! Az elektron azonban ekkor sem egyesül a maggal, ennek magyarázatát bizonytalansági elv adja meg, amely szerint a magban tartózkodó elektron rögzített pozíciója miatt az impulzus és emiatt a kinetikus energia ingadozása végtelenül nagy lenne.
Az elektron kvantummechanikai modellje atomokban
Az elektron mozgásának kvantummechanikai leírását a Schrödinger egyenlettel adjuk meg. Ekkor az állapotfüggvény változása mindhárom térkoordinátára kiterjed:
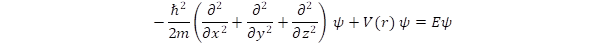
A centrális V(r) potenciál az atommag és az elektron Coulomb vonzását írja le. A differenciálegyenlet megoldására standard eljárásokat dolgoztak ki, amelynek sarokpontjait ismertetjük a módszer illusztrálása érdekében.
A V(r) potenciál nem függ az iránytól, ezért a hullámfüggvény a sugár és a polárszögek szerint szorzatalakban állítható elő: ψ(r) = F(r).Y(θ,ϕ). A derékszögű koordinátákról áttérünk a polárkoordinátákra:
x = r.sinθ.cosϕ, y = r.sinθ.sinϕ, z = r.cosθ
Ekkor a kinetikus energia felbontható két részre, az első az r sugártól, a második az iránytól függ és kifejezhető az impulzusmomentum négyzetével: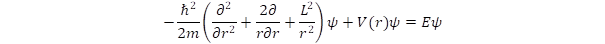
Az L impulzusmomentum operátora az r vektor és az p impulzus operátorának vektoriális szorzata, sajátfüggvénye az Yl,m(θ,ϕ) gömbfüggvény, ami az L operátor l(l+1) és az Lz operátor m = –l, –l+1, … l sajátértékéhez tartozik. Az állapotfüggvényt felírva a sugártól függő F(r) és a gömbfüggvény szorzataként kapunk egy kizárólag az r sugártól függő differenciálegyenletet:
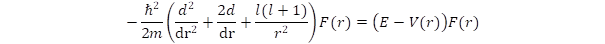
A differenciálegyenletből kiküszöbölhetjük az első rendű differenciált, ha Fl(r) = Rl(r)/r alakú függvényt keresünk, ekkor átrendezés után:
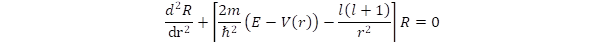
Hidrogénatomban V(r) = –e2/r. A szokásos módon ismét először az aszimptotikus megoldást keressük, amit majd egy véges rendű polinommal szorzunk meg. Nagy r értékeknél mind a potenciális energia, mind az impulzusmomentumtól származó kinetikus energia kis értéket vesz fel, ezért az R függvény aszimptotikus lefutásánál az egyenlet egyszerűsödik: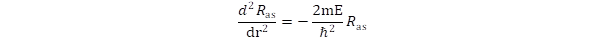
Csak olyan megoldást keresünk, amikor az elektron kötött állapotban van, tehát negatív az energiája, ekkor a reguláris aszimptotikus függvény:
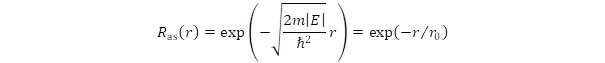
Itt r0 definíciója
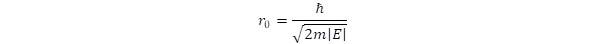
Mivel negatív energiájú megoldásokat keresünk így E = –ℏ2/(2m.r20). Vezessük be dimenziómentes változót, azaz:
ξ = 2r/r0::
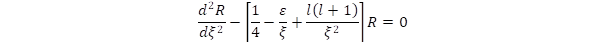
Folytatás a IV. részben: "Miért diszkrétek az energianívók kötött állapotban_IV"
További bejegyzések összefoglalója: "Paradigmaváltás a fizikában"