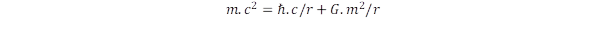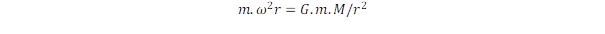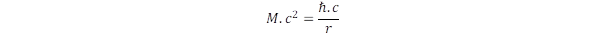Egy korábbi bejegyzésben (Determinizmus és kvantummechanika: a szabadság szintjei a fizikában) már áttekintettem a kvantummechanika néhány olyan jelenségét, aminek összehangolása szokásos fogalmainkkal nehézséget okoz és paradoxonokhoz vezet. Itt most részletesebben és szemléletes példákkal kiegészítve veszem elő ezeket a kérdéseket, elsőként a kétrészes kísérleteket, amelynek értelmezése a legvilágosabban mutatja a klasszikus fizika és a kvantumfizika eltérő szemléletmódjának okait.

Az EPR-paradoxon

A kvantummechanika értelmezési dilemmái ilyen vagy olyan módon a Heisenberg-féle bizonytalansági elvhez kapcsolódnak. Addig egyeznek az álláspontok, amíg nagyszámú részecske tulajdonságairól van szó, mert ekkor elfogadható a valószínűségekre alapozott statisztikai leírás. A kvantummechanikai korrespondencia elv szerint a határozatlansági törvények belesimulnak a makro-világban a klasszikus fizika determinizmusába. Más a helyzet, ha egyetlen foton, vagy elemi részecske tulajdonságait vizsgáljuk. Erre példa az Einstein, Podolsky és Rosen által felvetett gondolatkísérletek esete (EPR-paradoxon), melyek közül néhányat már tényleges kísérlettel is ellenőriztek.

A kétréses kísérlet

Az EPR-paradoxon talán legtöbb vitát kiváltó esetét képviselik a kétréses kísérletek. A kísérlethez monokróm fényforrást használunk, amelyik két keskeny (a hullámhosszal összemérhető) résen halad át és egy fényérzékeny ernyővel vizsgáljuk a beeső fény intenzitását. Eddig a kísérlet nem több mint a jól ismert interferencia jelenség megfigyelése: az optikai úthosszak különbsége által meghatározott helyeken fénymaximumokat és minimumokat észlelünk. A kísérlet akkor ad meglepő eredményt, ha egyesével indítjuk el a fotonokat, és külön-külön detektáljuk a felvillanásokat. Ebben az esetben ott tapasztalunk gyakrabban felvillanást, ahol interferencia maximum van és nincs felvillanás a minimum helyeken. Tehát nem az egyidejűleg kibocsátott fotonok közötti interferenciát látjuk, hanem az egyes fotonok saját magukkal lépnek interferenciába, ami arra mutat, hogy a foton egyszerre halad át mind a két résen!

Milyen információnk van a fotonról a kölcsönhatás előtt?

Ez a jelenség nem fordulhat elő a klasszikus fizikában, viszont jellemző a kvantumos állapotokra. Mi ennek az oka? Képzeljük magunkat a foton helyébe! Milyen információval rendelkezik a kölcsönhatás előtt? Olyan a helyzete, mint magunknak, ha az üres térben lennénk és semmilyen fény, semmilyen információ nem jutna el hozzánk. Ekkor nem jelentene számunkra semmit az irány fogalma. mert környezetünk nem adna számunkra semmilyen összehasonlítási lehetőséget. Emiatt a foton számára a tér fiktív! A foton terjedésérnek leírására mi mégis a szokásos térfogalmainkat használjuk, de mivel nem rendelhető semmilyen határozott irány a mozgáshoz, így azt mondjuk, hogy minden irányban egyenlő valószínűséggel terjed a fény.

A foton karakterisztikus tulajdonságai

A fotonról két dolgot azonban tudunk, egyrészt c sebességgel mozog, másrészt állapota periodikusan változik. A fénysebességű forgás modellben ez a periodikusság a forgásból származik, melynek frekvenciája határozza meg a foton energiáját is. A forgás miatt a foton minden időpillanatban egy kitüntetett fázissal rendelkezik, melynek értéke kizárólag a foton kibocsátásától számított időtől függ. De merre halad a foton, ha nincs irány? Jobbra, balra, előre vagy hátra? Ezeknek a fogalmaknak nincs értelme, ha nem beszélhetünk valódi mozgási irányról. A foton tehát minden időpillanatban tetszőleges irányban haladhat. Mozgásában kizárólag csak a fázis váltakozása játszik szerepet. Ennek felel meg a Huygens által felállított elképzelés, aki úgy értelmezte a gömbhullámokban történő terjedést, hogy minden időben és pontban a fény újabb gömbhullámot kelt és a gömbhullámok összegződése alkotja meg a terjedési képet. Ez kijelöl egy gömbhullám frontot, ameddig egyáltalán eljuthat a fény egy adott idő alatt és ez a front jól definiált fázissal rendelkezik. Mivel a foton mozgási iránya nem határozott, így a gömbön belül bármely ponthoz a foton különböző utakon is eljuthat, ezért a foton a teljes gömbben mindenütt jelen van. Tehát jelen van egyidejűleg mind a két résnél is.

Hogyan halad át a foton a réseken?

De mi történik a fotonnal, amikor eléri azt a felületet, ahol két rést alakítottunk ki? Ott ahol nincs rés sok-sok elektron van több rétegben is és a foton kölcsönhatásba kerülhet ezekkel az elektronokkal Két dolog történhet, vagy reakcióba lép valamelyik elektronnal az első rétegben, vagy tovább halad. Viszont minden ilyen „találkozás” időt vesz igénybe, így az optikai közegben a foton mozgása lelassul. Ez a jelenség okozza vízben és üvegben a fénytörést, ahol a fotonok többsége nem nyelődik el a közeg által. Ha viszont optikailag nagyon sűrű a közeg, akkor előbb-utóbb elnyelődik a foton, tehát a falon nem jut át. De azok a fotonok, amelyek néhány rétegen túljutnak esélyt kapnak, hogy átlépjenek a réseken. Még akkor is így van, ha egyetlen fotonról van szó, ezért mind a két résnél átbújik a foton. A foton ezt persze nem észleli, mert ha nem lép kölcsönhatásba egyetlen elektronnal sem, akkor a réseknél is a szokott módon, tehát gömbhullámokban terjed tovább. Ha végül eljut a fényérzékeny ernyőhöz, akkor attól függ a detektálás esélye, hogy mekkora az optikai úthosszak különbsége a két réstől számítva, ezért a detektálás gyakorisága megfelel az interferencia szabályainak.

A hullámfüggvény redukciója

A foton tehát a detektálás előtt a terjedési gömbön belül bárhol lehet, de a detektálása már csak egyetlen pontban történhet meg. Abban a pillanatban, amikor valamelyik elektronnal kölcsönhatásba lépett már nem lesz csak abban az egyetlen pontban, ahol az elektron tartózkodik. Amikor a kvantummechanika ezt a jelenséget leírja, akkor a hullámfüggvény redukciójáról beszél. A detektálás előtt a foton hullámfüggvénye az egész térrészben való előfordulást írja le, de a detektálás után már egyetlen pontra korlátozódik a foton pozíciója. Azt mondjuk ilyenkor, hogy a foton hullámtermészete megszűnik és a detektálás pillanatában már korpuszkulaként viselkedik. A hullámfüggvénynek ez a „redukciója” sok spekulációra adott már okot, sokan keresik azt a fizikai folyamatot, ami a foton, vagy az elektron állapotváltozását előidézte. Eddig a foton szempontjából vizsgáltuk a kérdést, de hasonló a történet az elektron oldaláról is, a detektáláskor az elektron állapotát leíró hullámfüggvény is „redukálódik” a kölcsönhatás bekövetkeztekor. Véleményem szerint azonban nincs egy rejtélyes fizikai folyamat sem a foton, sem az elektron hullámtermészetének megváltozása mögött, mert a változás az információban, az irány fogalmában történik, amikor a fiktívből reálissá válik. Detektáláskor ugyanis „látjuk”, hogy hová csapódott be a foton. Mégpedig azért látjuk, mert a fényérzékeny ernyőről rengeteg foton jut el hozzánk, ez valójában a „látás”. Tehát amikor a mérést kiértékeljük, akkor már nem csupán az egyetlen fotonról, amit megfigyelünk, kapjuk az információt, hanem a fotonok garmadájától. Ez a sok foton alakítja ki aztán „valós” irányképzetünket! Egyetlen fotontól nyert információról csak akkor beszélhetnénk, ha nem látnánk az egész berendezést, de akkor az egyetlen fotonról sem tudnánk semmit! Tehát ami megváltozik az nem a foton állapot redukciója, hanem az irányról alkotott fogalmunk.

Detektálhatjuk-e, hogy melyik résen halad át a foton?

Próbáljuk meglesni, hogy valóban egyidejűleg hatol-e át a foton a két résen, ezért helyezünk el egy-egy detektort mind a két rés mögött, de gondoskodjunk róla, hogy a detektorok után a foton változatlan elrendezésben érhesse el a fényérzékeny ernyőt. Azt fogjuk tapasztalni, hogy egyszerre csak az egyik detektor szólal meg. Ennek oka, hogy egyetlen foton mindig csak egyetlen elektronnal léphet kölcsönhatásba. Ebben az esetben viszont megszűnik az interferencia, azaz a fényérzékeny ernyőn egyenletes eloszlásban jelennek meg a felvillanások. Az interferencia elmaradásának oka, hogy a detektorból már megváltozott fázisú foton lép ki, és ez a fázis már véletlen módon összegződik a másik résen átjutó fotonéval.  

LINK a folytatáshoz: A kvantumvilág rejtélyei 2.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Elvek és egyenletek

A fizikai leírásban alapvető szerepet játszanak az egyenletek.  Ezen belül is differenciálegyenletek adják meg a mechanika, a kvantummechanika, az elektrodinamika, a termodinamika alaptörvényeit a kérdés azonban, hogyan definiáljuk a különböző törvényekben szereplő fizikai mennyiségeket. Szokásos ilyenkor az egyenletekből kiindulni és azon keresztül értelmezni a bennük szereplő mennyiségeket. Ezt nevezhetjük a matematikai gondolkodásmódnak, a fizikai gondolkodásmódnak azonban inkább megfelel a fordított út, amikor bizonyos alapelveket fogalmazunk meg és ez alapján jutunk el az egyenletekig.

A mechanika fogalmai

Induljunk ki a mechanikából. Egy mozgó test impulzusát mint tömegének és sebességének szorzatát szokás definiálni, azaz egy egyenlet áll a definíció mögött. Jobb ehelyett egy elvet megfogalmazni: Az impulzus az a fizikai mennyiség, ami egy test mozgásállapotát tartja fenn. Ez a definíció megfelel Newton első törvényének: minden test megtartja egyenes vonalú, egyenletes sebességű mozgását, amíg nem hat rá külső erő. Fogalmazzuk meg az itt fellépő újabb fogalom, az erő definícióját is. Itt Newton második törvényére szokás hivatkozni, mely szerint az erő a tömeg és a gyorsulás szorzata, tehát ismét egy matematikai egyenlet. Ehelyett ismét mondjunk ki egy elvet: az erő az a fizikai mennyiség, amelyik megváltoztatja a testek mozgásállapotát. Ebből már világos az erő és az impulzus kapcsolata: az erő megtartja, az impulzus megváltoztatja a mozgási állapotot.

Lépjünk tovább és határozzuk meg az energia fogalmát. Ezt gyakran a leejtett test potenciális (helyzeti) és kinetikai (mozgási) energiájával jellemzik. Kezdetben nem mozog a test, ekkor csak helyzeti energiája van. Az esés közben felgyorsul, a pillanatnyi sebességet a Newton-egyenlet segítségével határozhatjuk meg, majd a sebesség ismeretében kapjuk meg a mozgási energiát. Eredményül azt kapjuk, hogy a helyzeti és a mozgási energia összege állandó, azaz az energia megmarad. Ez az eljárás szintén a matematikai egyenletekre támaszkodva jut el az energia megmaradás törvényéhez. Az energia definíciója azonban épp a fordított gondolatmenetet kívánja meg: nem az energia megmaradásáról kell beszélni, hanem az energia az a fizikai mennyiség, amelyik a változó mozgásokban is megmarad. Épp ebben különbözik az impulzustól, amelyik csak az állandó sebességű mozgásoknál nem változik meg. Úgy is mondhatjuk, hogy az energia az állandóság a változásban.

Forgások és az impulzusnyomaték

Amit tehát a fizikában – és nem csak a fizikában, hanem más területeken is – vizsgálnunk kell, hogy mi az ami állandó, ami megmarad, és mi az ami változik, vagy változtat. De maradjunk a fizika területén és térjünk át a forgásokra. Ennek szemléltetésére gondoljunk a jégtáncosra, amikor a piruett figurát hajtja végre. Először széttárja a karját, majd kezével és egyik lábával a jégre rúgva lendületet vesz, amitől lassú forgásba kezd. Ezután kezeit szorosan a testéhez szorítja, amitől forgása felgyorsul. Vessük fel a kérdést: mi az a fizikai mennyiség, ami a forgás során állandó marad? Erre a válasz az impulzusnyomaték (impulzusmomentum). Tehát nem egy matematika formulával jutunk el a fogalomhoz, ami ez esetben az impulzus és a forgási sugár vektoriális szorzatával adható meg, hanem fordítva, ismét egy elv a kiindulási alap. Itt a matematikai definícióhoz azt is hozzá kell tenni, hogy a térben kiterjedt test esetén elemi pontokra kell felbontani a testet, minden egyes pontban meg kell adni az impulzust mint a kerületi sebesség és a ponthoz tartozó tömeg szorzatát, majd ezt kell szorozni a forgástengelytől való távolsággal és ezután az összes pontra összegezni (integrálni) kell. A helyes fizikai definícióban először az elvet kell megadni, majd ebből kell származtatni a matematikai eljárást és nem fordítva: megadni először a matematikai eljárást és ebből kimutatni, hogy a matematikai módszerrel adott definícióból már következik, hogy az így definiált mennyiség tényleg állandó a forgás során.

Az elemi részecskék spinje

Ha egy test impulzusnyomatékkal rendelkezik, akkor forog és véges kiterjedéssel (sugárral) rendelkezik. A részecskefizika általánosan elfogadott modellje (Standard Modell) szerint minden valóban eleminek tekinthető részecske rendelkezik impulzusnyomatékkal, azaz spinnel, ahol is a spin a redukált Planck állandó, azaz ℏ együtthatója. A fény elemi részecskéje, azaz a foton esetén a spin S = 1, míg az elektroné, protoné, neutroné ½. A fotonok energiája és frekvenciája a hosszúhullámú rádiófrekvenciás hullámoktól a gamma sugárzásig akár húsz nagyságrenddel is változhat, impulzusnyomatékuk, azaz spinjük mégis hajszálpontosan egyezik. Az S = ½ spinű (fermion) elemi részecskék tömege is különbözhet négy nagyságrenddel, lehetnek töltöttek és semlegesek is, viszont spinjük mégis azonos. A fizikai tankönyvek nem tárgyalják, hogy milyen fizikai jelenség okozza az impulzusnyomatékok egyezését, sőt arról sem írnak, hogy forognának-e ezek a részecskék, az elektron esetén pedig egyenesen pontszerűségről beszélnek. Tehát nem teljesülnek azok a kritériumok, amit minden impulzusnyomatékkal rendelkező fizikai objektumtól elvárnánk. Olyan állításokat is találhatunk, hogy a spin a részecskék saját (intrinsic) tulajdonsága, amihez nem köthető semmilyen klasszikus forgási kép, mert ezt a relativitáselmélet nem teszi lehetővé. Nézzük hát meg, hogy igaz-e az utóbbi állítás!

A speciális relativitáselmélet

A relativitás, pontosabban a speciális relativitás elméletét is valamilyen alapvető fizikai elvre lehet visszavezetni.  Ez az elv a fénysebesség állandóságának elve, ebből már a szokásos matematikai szabályok levezethetők. De miért állandó a fénysebesség és ez valójában mit jelent? Ezt abból következik, hogy az univerzumban minden kölcsönhatás véges sebességgel terjed, tehát nem csak az elektromágneses, hanem a gravitációs kölcsönhatás is. De miért létezik ez a határsebesség, ami nem léphető át semmilyen kölcsönhatásban és semmilyen fizikai objektum által? Ezt magyarázhatjuk egyrészt az univerzum végességével, mert ha az univerzum véges, akkor annak minden objektuma és minden tulajdonsága is véges. Ha végtelen lehetne a sebesség, akkor ezáltal végtelen távolságba juthatnánk egy szempillantás alatt. Másrészt a kölcsönhatások véges sebessége még akkor is szükségszerű, ha végtelen kiterjedésű lenne az univerzum. Képzeljük csak el, mi történne, ha például az egyik csillagrendszerből késleltetés nélkül érkezne meg valamilyen hatás a másikba? Ekkor a válasz is késleltetés nélkül jönne, majd hasonlóan a viszont válaszok végtelen sora. Ekkor a teljes hatás egy végtelen tagból álló mértani sorozat összege lenne, amelynek kvóciense, ha egynél nagyobb, akkor az univerzum felrobbanna, ha kisebb, akkor eltűnne. Viszont tudjuk, hogy az univerzum már milliárd évek óta létezik. Tehát a létezés maga megköveteli, hogy minden kölcsönhatásnak legyen véges határsebessége, ami nem más mint a fény sebessége vákuumban. De miért jelent a végesség egyúttal állandóságot is? Képzeljük el, hogy egy mozgó objektumból bocsátunk ki fényt. Szokásosan azt gondolnánk, hogy ekkor az objektum sebessége és a fényé összeadódik. De ha összeadódna, akkor átléphetnénk a határsebességet. Tehát ha van határsebesség, akkor nem adódhat össze az objektum és a fény sebessége. Ha viszont nem adódik össze, akkor nem is vonódhat ki. Ezért a fény kizárólag a határsebességgel mozoghat, amit szokásosan c-vel jelölünk. Ennek csak látszólag mond ellent, hogy vízben vagy üvegben a fény lassabban terjed. A lassabb terjedést a fotonok és a töltött részecskék kölcsönhatása okozza. Minden egyes „találkozáskor” a fény vagy elnyelődik, vagy tovább halad, de az utóbbi esetben a kölcsönhatás késleltetést idéz elő. És minél többször lép kölcsönhatásba a fény és az elektronok, annál lassabb lesz a terjedés sebessége.

A Lorentz kontrakció és a relativisztikus tömegnövekedés

A sebességet a megtett út és az idő hányadosa adja, ezért ha a sebesség nem adódik össze a szokott módon, akkor ez a megtett hosszakra is igaz. Következésképp a megtett út rövidebbnek látszik. Minden távolságot valamilyen fizikai objektum hosszához viszonyítjuk, ezért a tárgyak hossza is rövidülni fog. Ezt nevezi a relativitáselmélet Lorentz kontrakciónak.  A hétköznapi életben megszokott sebességeknél ez azonban elhanyagolható mértékű, viszont jelentős lesz, ha közeledünk a fény sebességéhez. A fénysebesség pedig egy olyan elvi határ, ahol már a c sebességgel mozgó objektum mérete nullára zsugorodik.  Képzeljük el, hogy egy méterrudat tartok vízszintesen az vonat ablaka előtt párhuzamosan a vonat haladási irányával. Ekkor ez „kintről”, tehát a sínek mellett, rövidebbnek látszik. De ez fordítva is igaz, ha kint tart valaki a kezében egy méterrudat, azt én látom rövidebbnek. Ebben nyilvánul meg a relativitás: a testek mérete nem abszolút, hanem attól függ, hogy a testtel együtt haladó rendszerből (vonatból) nézzük, vagy kívülről. Ha viszont valaki kint eldob egy súlygolyót párhuzamosan a vonat haladási irányával, akkor a dobást kisebbnek látjuk, ami a dinamika szerint akkor lehet, ha megnövekszik a súlygolyó tömege. Ha viszont a vonatunk képes lenne fénysebességgel mozogni, akkor a „kinti” méterrúd hossza nulla lenne, a súlygolyó tömege pedig végtelen nagyra nőne. Viszont a külső megfigyelő számára ez úgy jelentkezne, hogy nullahosszúságúnak látná a szerelvényt, és végtelennek tartaná a tömegét. Ez a végesség kritériuma miatt nem lehetséges, azaz a „vonat” nem érheti el a fény sebességét. Ez vonatkozik valamennyi tömeggel rendelkező fizikai objektumra is: sebességük nem érheti el a határsebességet.

A fény különös természete és a tömeg keletkezése

Létezik azonban egy olyan fizikai objektum, amelyik a határsebességgel mozog, ez a fény, illetve annak kvantuma a foton. Ez az előbbiek szerint úgy lehetséges, ha nulla tömeggel rendelkezik, azaz nincs nyugalmi tömege. Viszont a relativitáselmélet legfontosabb felismerése, hogy a tömeg és az energia ekvivalens, amit az E = m.c² összefüggéssel lehet kifejezni. A foton viszont rendelkezik energiával, amely arányos a rezgési frekvenciával (ν illetve ω = 2π.ν) az E = h.ν = ℏ.ω összefüggés szerint. Tehát az ekvivalencia elv szerint a foton mégis rendelkezik tömeggel! Hogyan lehetséges ez, hiszen az imént még azt jelentettük ki, hogy a fotonnak nincs tömege! Az ellentmondás úgy oldható fel, ha kétféle tömegről beszélünk, az egyik a nyugalmi a másik a mozgási tömeg. A foton nyugalmi tömege határértékben nulla, miként 1/X, ha X minden számnál nagyobb, azaz végtelen. Ekkor bár 1/X minden határnál kisebb szám, de ha szorozzuk X-szel, azaz képezzük az X*(1/X) szorzatot, mégis az egységet, tehát véges értéket kapunk. Legyen hát a fénysebességű mozgáshoz tartozó tömegnövekedési tényező az X szám és 1/X a foton nullához végtelenül közeli nyugalmi tömege, ekkor érthetővé válik, hogyan lehet a foton tömege egyrészt nulla, másrészt véges mennyiség. Evvel eljutottunk a relativitáselmélet másik alapvető fontosságú elvéhez: a fénysebességű mozgás anyagot (tömeget) hoz létre. Ez az elv egyébként kiolvasható a tömeg és energia ekvivalenciájának képletéből is: E = m.c², ahol a tömeget létrehozó fénysebesség négyzete hozza létre a kapcsolatot a tömeg és az energia között! A fotonnak azonban impulzusa is van, ami a már említett elv szerint fenntartja a fénysebességű mozgást. Az elektrodinamika szerint a foton p impulzusa arányos az energiával az E = p.c összefüggés szerint. Az arányosság következik a fénysebességű mozgás elvéből is, hiszen ekkor p = m.c az impulzus, amit c-vel szorozva kapjuk az m.c² energiát.

A foton impulzusnyomatéka

A fotonnak azonban impulzusnyomatéka, azaz spinje is van. Tehát a fotonnak a haladó mozgás mellett valamilyen forgást is kell végeznie. Adjunk ezért új értelmezést a foton energiáját és időbeli hullámait jellemző  ω körfrekvenciának és azonosítsuk ezt a forgás szögsebességével. Ha a forgás r sugarú kört hoz létre, akkor ennek kerületi sebessége u = r. ω lesz. Az r sugár nagyságának azonban határt szab, hogy az u sebesség nem lehet nagyobb, mint a c fénysebesség. A foton viszont fénysebességgel terjed, ezért bármilyen egyéb mozgással összekapcsolva is változatlan lesz az eredő sebesség, tehát a forgás kerületi sebessége is c lesz. Emiatt viszont az ω szögsebesség meghatározza a kör sugarának értékét is, azaz r = c/ω lesz. Ez a sugár pedig megegyezik a fény hullámhosszával! Az I-vel jelölt impulzusnyomatékot a mechanika úgy számítja ki, hogy szorozza a test impulzusát a forgási sugárral: I = p.r = m.c.r. Felhasználva két elvet: a tömeg és energia ekvivalenciáját: m = ℏ.ω /c² és a fénysebességű forgásét: r = c/ω, majd az m tömeg és az r sugarat behelyettesítve azt kapjuk, hogy az impulzusnyomaték I = ℏ, azaz a foton spin S = 1. Az impulzusnyomaték tehát nem függ az szögsebességtől és így érhetővé válik, hogy miért azonos a foton impulzusnyomatéka bármekkora is legyen az energiája.

A fénysebesség mint univerzális állandó

De vessük fel a kérdést, hogy mi az, ami a fénysebességű mozgásokat végzi és ezáltal anyagot, tehát tömeget hoz létre? A kérdéshez először a mozgás fogalmát kell megérteni. A mozgás a tér és az idő kapcsolata, ami matematikailag úgy fejezhető ki, hogy a tér egyes pontjait az idő mint változó függvényeként írjuk fel. Ennek a kapcsolatnak az univerzális – tehát a leíráshoz választott rendszertől független – formája, amikor fénysebességű mozgás jön létre. A fénysebességű mozgás ugyanis az egyetlen abszolút kapcsolat a tér és az idő között. Minden sebesség relatív, mert nincs az univerzumnak olyan centruma, amihez viszonyítva a testek mozgási sebességét egyértelműen megadhatnánk. Ha a vonaton átmegyünk az egyik szerelvényből a másikba, akkor beszélhetünk a vonathoz képesti sebességről, de meghatározhatjuk a sebességet a külső környezethez is. De ez sem abszolút sebesség, mert a Föld forog a tengelye és kering a Nap körül, tehát választhatnánk a Napot, amihez viszonyítjuk a mozgásunk sebességét. De ez sem abszolút, mert a Nap is kering a Tejútrendszerben, sőt ennek centruma sem abszolút vonatkoztatási rendszer, mert a Tejút is változtatja helyét a többi galaxishoz képest. Ugyanakkor bármilyen mozgást is végezzen egy fizikai objektum az általa kibocsátott fény sebessége mindig azonos lesz. A fénysebességű mozgások tehát univerzális kapcsolatot hoznak létre a tér és az idő között. A tér pontjai, melyeket egyébként csak matematikai absztrakciónak tekintünk, a fénysebességű mozgás által anyagi valóságra, azaz tömegre tesznek szert. Ezek lesznek a részecskék! Eddig csak a fotonnal foglalkoztunk, amit tehát egy forgó és egy haladó mozgás kombinációjával írunk le, de most terjesszük ki ezt az elvet valamennyi elemi részecskére!

Az elektron és a kettősforgások

Az S = ½ spinű elemi részecskék (fermionok) nyugalmi tömeggel rendelkeznek. Hogyan jön létre ez a tömeg?  Kézenfekvő a feltevés, hogy a fotonok mozgási tömegéhez hasonlóan fénysebességű mozgásokból. Fénysebességű haladás viszont nem jöhet szóba, tehát csak fénysebességű forgások hozhatják létre a nyugalmi tömeget. A foton pozíciójához nem rendelhető a tér egy kijelölt pontja, más a helyzet a fermionokkal, amihez minden pillanatban rendelhetünk egy tartózkodási helyet. Ez egyébként a kvantummechanika bizonytalansági elvéből is következik: a foton pontos impulzussal rendelkezik, ezért határozatlan a pozíciója, a fermionoknak rögzíthető a helyzete, de ez impulzusának bizonytalansága alapján történhet meg. A pozíció kijelölése az által valósulhat meg, ha két egymásra merőleges forgás kapcsolódik össze, ami létrehoz egy gömbfelületet. Nevezhetjük ezt a kettősforgást gömbforgásnak is. A két összekapcsolt forgás egymáshoz képest kétféle sodrásiránnyal rendelkezhet, az egyiket nevezhetjük jobb- a másikat balsodrásúnak. Ez a háromdimenziós tér sajátsága, amiben kijelölhetjük az egymásra merőleges x, y és z tengelyeket akár a jobb, akár a balkéz irányaival is. Ez a két rendszer nem forgatható egymásba, de egymásnak tükörképe. Ezt a tükrözési szimmetriát nevezzük kiralitásnak. Ez a kép mindjárt magyarázatot ad arra, hogy miért létezik világunkban anyag és antianyag: az egyik lehet a jobb- a másik a balsodrású kiralitás. A másodlagos forgások ellentétes perdülete kiolthatja egymást létrehozva az egytengelyű forgást. Ez felel meg annak, amikor az anyag és antianyag annihilál és gammasugárzást hoz létre.

Mit jelent az elektron pontszerűsége?

A részecskefizika az elektront pontszerűnek tekinti, amit kísérletileg a Bhabha szórás támaszt alá: amikor az elektronokat pozitronokkal bombázzák. Ekkor olyan szórási képet kapunk, mintha a töltések egyetlen matematikai pontba sűrűsödnének össze. A pontszerűség elve viszont ellent mond annak, hogy az elektronnak van impulzus és mágneses nyomatéka is. A látszólagos ellentmondás azonban feloldható fénysebességű forgások esetén. Az r sugarú kör kerülete 2r.π, az r sugarú gömbbé 4r². π. A mozgás irányában azonban a távolság lecsökken a Lorentz kontrakció szerint, ami fénysebességű mozgásnál nulla lesz. De ez csak a mozgás irányában érvényes, arra merőlegesen nem változik a távolság. Mivel a sugár merőleges a körforgás irányára így annak ellenére, hogy a kerület, illetve gömbforgásnál a felület nullára csökken, a sugár változatlan marad. A felület eltűnése miatt így a Bhabha szóráskísérletben azt várjuk, hogy a hatáskeresztmetszet nulla lesz, míg a sugár nem változik létrehozva az impulzus és a mágneses nyomatékot.

Mekkora az elektron spin?

A kettősforgás arra is magyarázatot ad, hogy miért éppen fele a fermionok impulzusnyomatéka a fotonhoz képest. Mivel két független forgás alkotja a részecskét, így a forgás fenntartásához elegendő fele akkora impulzusnyomaték is. Minden forgás azonban létrehoz egy kifele mutató centrifugális erőt, ezt érezzük a körhintában is, de ez hat a Földre is a keringő mozgás miatt. Hasonlóan beszélhetünk kifelé húzó erőről az atomban is az elektronok mozgása miatt. A forgás fenntartásához szükség van egy ellenerőre, amit centripetális erőnek nevezünk. Ennek iránya pont ellentétes a centrifugális erővel és azt kompenzálni tudja. Ez a centripetális erő a körhintában a székeket a tengelyhez rögzítő kényszerhatás, a Föld keringésénél a gravitációs erő, az atomban a negatív töltésű elektronok és a pozitív töltésű atommagok közötti elektromos vonzás. Fölmerül a kérdés, hogy ha az elemi részecskéket a fénysebességű forgás hozza létre, akkor milyen erő egyenlítheti ki a centrifugális erőt?

Gravitáció: az általános relativitáselmélet

A magyarázat megtalálásához a fizika egy újabb fejezetét kell megnyitni, a gravitáció eredetét magyarázó általános relativitáselméletet. Ennek alapelve, hogy a gravitáció a tér görbületétől származik és ezt a görbületet a tömeg hozza létre. A háromdimenziós tér görbületét nehéz elképzelni, ezért gondoljunk ezért egy síkra, például egy gumimatrac felületére. Helyezzünk rá apró gyöngyöket, majd egy nehéz súlygolyót, ami a matracot belapítja. Ekkor a bemélyedés irányában a gyöngyök odagurulnak a mélyedésbe. Ha nagyobb súly helyezünk oda, akkor a gyöngyök gyorsabban és nagyobb távolságból fognak odagurulni. Ebben a képben a kétdimenziós vízszintes sík a mélységi, tehát a harmadik dimenzió irányában görbül be. Háromdimenziós tér esetén viszont a kiegészítő dimenzió már a negyedik lesz, ami a Minkowski által bevezetett négydimenziós téridőben képzelhető el azáltal, hogy a háromdimenziós tér az idő irányában görbülhet meg. Ennek a görbületnek két típusa lehet, az egyik felel meg az általános relativitáselmélet szokásos makroszkopikus térszerkezetének, a másik pedig az elemi részecskéket alkotó mikroszkopikus torzulás. Foglalkozzunk először az előbbivel, mert ez hozza létre a szokásos gravitációs vonzást. Itt most megmutatom, hogy ez a görbület visszavezethető a speciális relativitáselméletre.

A bolygómozgás Kepler törvényei

Induljunk ki a bolygómozgás Kepler törvényeiből. A további gondolatmenet nem kíván ugyan matematikailag nehezen áttekinthető lépéseket, mégis inkább a blog korábbi bejegyzésére utalok (Térgörbület és gravitáció forgó rendszerekben) , mert célom az elvek kiemelése, ami háttérbe szorulhatna a matematikai levezetések során. Kepler a csillagászati megfigyeléseket felhasználva kapcsolatot állapított meg a bolygók Naptól való átlagos távolsága és a keringési idő között: minél távolabb van egy bolygó a Naptól, annál hosszabb idő alatt tesz meg egy teljes fordulatot. Ezt a szabályt magyarázta meg Newton, amikor felírta a gravitációs törvényt, mely szerint két tömeg között akkora vonzó erő jön létre, ami arányos a tömegekkel, de ereje csökken a távolsággal. Ezt a törvényt kívánom magyarázni a speciális relativitáselméletből ismert Lorentz kontrakció segítségével.

Lorentz kontrakció és a gravitáció Newton törvénye

A bolygó keringése során a teljes pálya hossza kissé megrövidül a Lorentz kontrakció miatt, aminek mértéke keringés sebességétől függ a fénysebességhez viszonyítva. A keringő mozgás sajátossága, hogy ha kicsi a bolygó tömege a Naphoz képest, akkor a pálya független a bolygó tömegétől, csak a Nap tömege és a Naptól való távolság számít. Ebből következik, hogy a határértékben nullatömegű térpontok is ugyanolyan pályán mozoghatnak a Nap körül, mint az egyes bolygók. Más szóval maga a tér végezhet körforgást bármely tömeggel rendelkező objektumok körül. A Lorentz kontrakció miatt a pálya hossza rövidülni fog, tehát nem az euklideszi geometriában megszokott 2r.π határozza meg a kör kerületét, hanem ennél kisebb lesz, amit úgy írhatunk le, hogy a valódi sugár helyett egy kisebb „kerületi”, vagy „relativisztikus” sugárról beszélünk. Ezt a rövidebb sugarat hasonlítsuk össze a valódi, azaz a keringő testnek a centrumtól való távolságát mérő sugárral ,és a két sugár arányával jellemezzük a tér görbületét. Ha nincs rövidülés, azaz a két sugár hossza azonos, akkor a tér nem torzul. Ellenkező esetben viszont ez a torzulási arány határozza meg a gravitációs erőt. Ebből a felfogásból indulva eljuthatunk a gravitáció Newton törvényéhez.

Erős gravitáció: a részecskék forgását fenntartó erő

Ezen a sikeren felbátorodva, most nézzük meg, hogy mekkora erőt kapunk, ha a fénysebességű mozgás miatt a pálya kerülete nullára csökken, azaz a két sugár aránya nulla lesz!  Ezt tekintjük extrém mértékű mikroszkopikus torzulásnak. Mivel a mechanika elvei szerint az erő a potenciális energia térbeli változására vezethető vissza, ezért azt vizsgáljuk, hogy egy adott frekvenciával és a hozzá tartozó m mozgási tömeggel rendelkező részecskének mekkora lesz a potenciális energiája, ha a torzulás extrém mértékű a fénysebességű forgás miatt! Az itt nem közölt, de a korábbi bejegyzésben bemutatott számítás szerint a potenciális energia –m.c² lesz! Tehát pontosan megegyezik az m.c² nyugalmi energiával! Ez a nyugalmi energia azonban éppen hogy nem „nyugalmi”, hiszen fénysebességű forgástól származik és megfelel a forgás kinetikus energiájának. (Itt meg kell jegyezni, hogy a nem relativisztikus mechanikában a kinetikus energia kifejezésében szerepel az ½ együttható, de ez a formula csak kis sebességeknél érvényes, a fénysebességű mozgásnál az ½ együttható már elmarad).

A potenciális energia tehát pontosan kiegyenlíti a mozgási energiát, és ebből származtathatjuk a centrifugális és centripetális erőket, amelyek ellentétes irányban hatnak és kompenzálják egymást. Ezt a részecske forgást stabilizáló erőt nevezem erős gravitációnak. A fénysebességű elemi forgások tehát extrém mértékű, de rendkívül parányi kiterjedésű mikro-torzulásokat (tüskéket) hoznak létre a tér szerkezetében. Ezek a parányi torzulások viszont maguk körül lankás –  de nagy távolságba ható – torzulásokat hoznak létre, melyek összegződnek és a hatalmas számú részecske révén létrehozzák a szokásos gravitációs teret.

A forgásmodell kapcsolata a húrelmélettel

Az előzőek szerint a nyugalmi tömeggel rendelkező részecskéket két fénysebességű forgás hozza létre, melyek felülete nulla kiterjedésű, de mégis véges a sugaruk, tehát két dimenzió elvesztése miatt valójában egydimenziós alakzatok. Ebből a szempontból hasonló szerepet játszanak mint napjain fizikájában a húrok, szuperhúrok, bránok, vagy M-alakzatok és még sorolhatnám a divatos elméletek sorát. Az egydimenziós húrok rezgési frekvenciája határozza meg a részecskék tömegét és minél rövidebb a húr, annál nagyobb a tömeg, illetve az energia. Az említett elméletek viszont a szokásos négydimenziós teret további dimenziókkal egészítik ki, melyeket semmilyen kísérleti tapasztalat nem támaszt alá, ráadásul a modellek nem értelmezik az anyag és antianyag kettősségét, nem magyarázzák a spin eredetét és az elektromos töltést sem. Az általam javasolt kép épp fordított irányban ad magyarázatot a részecskék szerkezetére, mert a forgó gömb sugara nem a négydimenziós téridőt kiegészítő további dimenzió, hanem ellenkezőleg a három térbeli dimenzió egyre való redukciója a fénysebességű mozgás miatt.

A mozgás két arca: térgörbület és fénysebességű forgások

A fénysebességű forgás és a tér extrém mikroszkopikus torzulása ugyanannak a jelenségnek a kétféle megközelítése. Mert mi az a mozgás? A tér és az idő dimenziójának összekapcsolása. Ha forgásról beszélünk, akkor a térkoordináták függését vizsgáljuk az idővel kifejezve, ha a forgások által előidézett tértorzulást tárgyaljuk, akkor megfordítjuk a képet és az idő mértékét keressük a tér különböző helyein. Az általános relativitáselmélet szerint más tempóban száguld az idő (az óra lassabban jár) az erős gravitációs terekben, ez az idő dilatáció jelensége. A foton nem is érzékeli az időt, számára a milliárd éves út megtétele egy másik galaxisból csupán egyetlen pillanat. A részecske forgások kerületi sebessége, azaz a c, a nullahosszúságú kerület és a nulla idő aránya. A matematikai analízis szerint  két nullához végtelenül közeli mennyiség aránya lehet véges, ezt nem más mint a differenciálhányados. A sebességet is úgy számítjuk ki, hogy meghatározzuk az arányt a végtelenül rövidnek tekintett út és a végtelen rövid idő között. A matematikai fogalmak fontosak a fizikai törvények megértéséhez, akkor is, ha nem az egyenleteket tekintjük a fizikai elvek alapjának, hanem fordítva a fizikai elvek irányából közeledünk a matematikai egyenletek felé.

Az elektromágnesesség és a Coriolis erő

A modern fizika az elektromosan töltött részecskék közötti kölcsönhatást is kvantumos jelenségként kezeli. Ennek elve, hogy a töltések virtuális, azaz kísérletileg megfigyelhetetlen fotonokat bocsátanak ki és nyelnek el és ezek a fotonok hozzák létre a töltések közötti elektromos kölcsönhatást. Ez az un.  kvantum térelmélet. Az elmélet jól értelmezhetjük, ha a részecskék fénysebességű forgásaiból indulunk ki. A forgások során a már említett centrifugális erőn kívül megjelenik a Coriolis csavaró erő is, ha a forgó rendszeren belül valamilyen objektum mozgást végez. Ennek jól ismert példája, amikor a Föld forgása összekapcsolódik a sarkoktól az egyenlítő irányába történő légköri mozgással vagy tengeráramlással. Ez a Coriolis erő az áramlást megcsavarja és örvényeket, körbefutó áramlatokat hoz létre. Az áramlatok sodrásiránya ellentétes a Föld északi és a déli féltekéjén. Ennek oka, hogy a két esetben ellentétes a forgáshoz viszonyítva az áramlási irány. Hasonló a helyzet a részecskék kettős forgásánál, ahol az egyik forgás a Coriolis hatáson keresztül megcsavarja a másikat. A két eredeti forgás királis szimmetriája szabja meg, hogy milyen lesz a csavarodás körbefutási iránya. A Coriolis erő ily módon egytengelyű forgásokat indukál, ami értelmezésünk szerint nem más mint a foton. A Coriolis erő nagysága a mozgások sebességétől függ, és mivel a sebesség valamennyi részecskénél a fénysebesség, így a kölcsönhatás nem függ a tömegtől és valamennyi töltött részecskénél azonos. Evvel magyarázzuk, hogy az elemi töltés miért azonos valamennyi megfigyelhető elemi részecske esetében. A proton, neutront és hasonló összetett részecskéket alkotó, de kísérletileg megfigyelhetetlen kvarkok kivételt képeznek, mert az elektronhoz képest törttöltéssel rendelkeznek. Ennek oka a kvantummechanikai szuperpozíciós elv, aminek értelmezésével más bejegyzésben foglalkoztunk.

A kölcsönhatások mezőelmélete

A mikrovilág fizikai törvényei kvantumos alakban jelennek meg, emiatt alakult ki a fizikusokban az a meggyőződés, hogy minden kölcsönhatás, minden erő csak kvantumos lehet. Ezen az alapon próbálták meg kidolgozni az egységes mezőelméletet. (Elterjedtebb, de félreérthető térelmélet elnevezés). A mezőelméletben az elektromágneses kölcsönhatást a virtuális fotonok közvetítik, sikerült közvetítő részecskét definiálni az atommagokat  és azok alkotóit, a nukleonokat, valamint a kvarkokat összekötő erős kölcsönhatásra, amit gluonnak neveztek el, úgyszintén felfedezték a részecskéket egymásba alakító gyenge kölcsönhatás közvetítőit is, nem sikerült azonban az egységes mezőelméletbe bevonni a gravitációt. . Ennek oka, hogy nem a kvantumokra kell visszavezetni a gravitációt, hanem fordítva a gravitációs erő alapján lehet értelmezni a kvantumot. Ilyen alapon jutottam el a részecskék fénysebességű forgásaira alapozott részecskemodellhez, amelyben nem csak az elektromágneses kölcsönhatást, hanem az erős és gyenge kölcsönhatást is értelmezni lehet, de erre itt nem térek ki, helyette korábbi bejegyzésekre utalok (Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása, Barangolás a kvarkok és elemi részecskék világában, A Dirac egyenlettől az általános fermion egyenletig). Az általam felépített fizikai modellben minden kölcsönhatás azáltal jön létre a fizikai objektumok között, hogy az elemi, kéttengelyű forgások, azaz a részecskék megváltoztatják a környező teret, abban másodlagos forgásokat hoznak létre. Ennek egyik formája, amikor egytengelyű fénysebességű forgások, azaz fotonok lépnek ki és nyelődnek el. Ennek felelnek meg a kvantum térelméletben a virtuális fotonok. 

A részecske környezetének másik perturbációja a gravitációs erő, amely, bár a távolság függvényében azonosan csökken, mint az elektromágneses kölcsönhatás mégis alapvetően eltér abban a tekintetben, hogy függ a részecskék tömegétől. Úgy is fogalmazhatunk, hogy a gravitációs vonzás a részecskék forgási frekvenciájától, míg az elektromágneses a forgás kerületi sebességétől függ. Mivel ez utóbbi mindig a fénysebesség, ezért az elektromos töltés, ami a kölcsönhatás hordozója minden részecskében azonos, de előjele függ a részecske királis szimmetriájától. A kétféle előjel avval magyarázható, hogy a kiralitás determinálja a kibocsátott és elnyelt fotonok forgásának polarizációs irányát. Az előbbiek értelmében a két távolba ható kölcsönhatás úgy fogható fel, hogy az elemi forgások hatása túlterjed a részecskék saját sugarán, más szóval az elemi forgás megváltoztatja a környező teret. Mi határozza meg ennek mértékét? Erre jelenleg nem ad választ a fizika, ez úgy tekinthető mint egy „csatolás” a részecske és a környezete között, ami a tér valamilyen belső sajátsága. A csatolás mértékét az elektromágneses kölcsönhatásban a Sommerfeld-féle állandó (1/137), a gravitációét a gravitációs állandó határozza meg.

Fölvetődik a kérdés, hogy miért nem lehetett a gravitáció kvantumelméletét kidolgozni? Azért, mert ennek a kölcsönhatásnak nincs kvantuma. Miért? Mert a kvantum az elemi forgáshoz tartozó impulzusmomentum, azaz a spin. Az elemi forgás pedig fénysebességű forgást jelent. A gravitáció esetén lassú és a távolság függvényében csökkenő frekvenciájú forgások jönnek létre a gyorsan forgó részecskék körül. Minél nagyobb frekvenciájú a részecske forgása, annál erősebben változtatja meg a mozgás a környező teret. Mivel ez a lassú forgás nem éri el a fénysebességet, így nem járul hozzá tömeg és impulzusmomentum. Ha pedig nincs spin, akkor kvantum se lehet, mert minden kvantum a spinhez kapcsolódik.

Az egységes fizikai világkép: a téridőrészecske

A világ egységes, amit egységes fizikai világképpel írhatunk le. Ennek fontos lépését tette meg Minkowski, amikor bevezette a téridő fogalmát. A tér nem lehet meg idő nélkül, ami fordítva is igaz. A két fogalom áthatja egymást, aminek egyik megfogalmazását adja meg a speciális, a másikat az általános relativitáselmélet. Innen lépünk eggyel tovább, amikor a részecskéket is bevonjuk a fogalomkörbe, mert a részecskék nem külön létezők a téridőben, hanem a téridő speciális megnyilvánulásai a mozgásokon keresztül. Definiálhatjuk a részecskéket a tér elemi, azaz fénysebességű forgásaival, de értelmezhetjük a tér mikroszkopikus görbületei által is. A két értelmezés ekvivalens. A tér viszont azáltal válik leírhatóvá, hogy léteznek benne az elemi forgások, amelyek egymással kölcsönhatásba lépnek és ezáltal értelmet adnak a távolság és az irány fogalmának is. Részecskék nélkül nincs értelme térről beszélni. Ugyanez elmondható az idő és a részecskék kapcsolatáról is. Az idő úgy jelenik meg, ha a részecskék egymáshoz való viszonyát és átalakulásait sorba rendezzük és megkülönböztetjük egymástól az okot és az okozatot és ennek vég eredményeképpen kibontjuk a fizikai idő fogalmát. Az egységes fizikai világkép alapját egyetlen fogalommal a téridőrészecskével adhatjuk meg. Evvel kifejezzük, hogy nincs tér és idő részecskék nélkül, és nincs részecske téridő, azaz mozgások nélkül.

Az ősrobbanás mint fénysebességű kaotikus mozgás

Alkalmazzuk ezt a szemléletet az ősrobbanás elméletében is. Az elmélet kiindulópontja a táguló univerzum, ami a távoli galaktikák vörös eltolódásából következik. Az elmélet másik sarokpontja, a mikrohullámú háttérsugárzás jelensége. Az elmélet szerint az ősrobbanás korai szakaszában először az elemi részecskék alakultak ki, majd ezek összekapcsolódása hozta létre az atommagot, majd az atomokat és később jöttek része az összetettebb objektumok és a csillagok. Ezt megelőzően a kvarkok és gluonok plazmáját tételezik fel. Ez a feltevés szerintem nem állja meg a helyét, mert kvarkokat csak a hadron típusú részecskék (ide tartozik a proton és neutron is) összetevőiként lehet megfigyelni, ezért nem indokolt, hogy létezésük megelőzze az őket stabilizáló formációk keletkezését. A fénysebességű modellből az következik, hogy a kezdeti ősállapot fénysebességű, pulzáló mozgásokból állt, ezek kaotikus mozgások voltak, melyben a gyors ütközések megakadályozták a forgási állapotok kialakulását. Az univerzumnak ebben a korai korszakában tehát nem voltak elemi forgások, így a kvantum sem létezett, ez volt az univerzum kvantum előtti állapota.

 Minél nehezebb egy részecske, annál nagyobb frekvenciájú forgás tartozik hozzá. Amikor az ősállapot kezdett lehűlni már elég volt az idő az ütközések között, hogy a legnehezebb részecskék kialakuljanak, majd később jöhetett létre a könnyebb elektron is. Az utána következő fázis már megfelelhet az ősrobbanás elméletének jelenleg elfogadott menetének. Van azonban az elméletnek egy gyenge pontja, mert nincs meggyőző magyarázat arra, hogyan vált uralkodóvá az anyag az antianyag felett. A nagy energiájú folyamatok a részecske fizika szerint egyszerre hoznak létre mindig egy részecskét és egy antirészecskét, ezért az annihilációs folyamatok nem tennék lehetővé az anyagban túlsúlyos univerzum kialakulását. Ez a dilemma feloldható kaotikus fénysebességű mozgások esetén, mert ekkor a véletlen szabályai uralnák, hogy a rendezetlen mozgásokból éppen milyen részecskék alakulhatnak ki, tehát ekkor nem kötelező, hogy egyidejűleg részecskepárok jöjjenek létre. A részecskék és antirészecskék száma a statisztika szabálya szerint eltérhetnek egymástól és így a rendezetlen ősállapotból a rendezett forgások világába átmehetett az univerzum a protonok és elektronok véletlen szülte többlete által.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Színhely: Műcsarnok, 2015 december 5

Az emberi gondolkozás szintjei az ókori , mai, a fizikáé, enyém, hallgatóságé

Szemléltetés: az ősrobbanás és a teremtésmítoszok kapcsolata

Vita: rövid kérdések közben, a végén lehet hosszabb álláspontokat kifejteni.

Az ókor: teljesség,  modern kor fragmentált, leszűkített gondolkozására.

Módszer: Virtuális diák

Dia 1: A valóság, mint fizikai objektum, szétdarabolás, alak?

Dia 2. Puzzle: A részek ismerete nem tárja fel a motívumot

Dia 3. Bábel tornya és a tudomány szétaprózottsága. C.P. Snow: A két kultúra (humán és reál)

Cél: összeillesztés az egyes elemek ismeretében

Szakterület: elektronok mágneses tulajdonságai, aminek alapja a spin

Mi a spin? A Dirac egyenlet által bevezetett fizikai mennyiség.

Összhang keresés: Átfogó, ellentmondásmentes fizikai szemléletmód kialakítása a fizikában

Negatív fizikus vélemények.

Mi a modern fizika gondolkodásmódjának legfőbb hibája:

Belevész az egyenletekbe és eltolja magától a fizikai fogalmak értelmezését

Cél: Összességében látni a fizika világát, melynek alkotóeleme az ősrobbanás

Fizikai elvek kimondása matematikai egyenletek helyett!

Impulzus, erő és energia

Kulcs: az állandóság és a változás viszonya

Dia 4: piruett figura a jégtáncban

Dia 5: Kerekes kút

Impulzus-nyomaték, spin

Hogyan lehet egy pontszerű részecskének nyomatéka?

Az összeillesztés módja

Elem_1: speciális relativitáselmélet: Mi az alapelv? A kölcsönhatások véges sebessége. Ez egy még általánosabb törvényből adódik: egy VÉGES rendszerben minden tulajdonságnak végesnek kell lenni.

ÁLLANDÓ:  fénysebesség

VÁLTOZÓ (relatív) : tömeg, távolság

Elem_2: a foton fénysebességgel terjed: nulla nyugalmi tömeg, de E = m.c²!

Elem_3: X*1/X = 1  A nulla és végtelen szorzata lehet véges!

A fénysebesség tömeget (anyagot) hozhat létre!

Elem_4: részecskefizika

Minden tömeget a fénysebességű mozgás hoz létre! Nyugalmi tömeg: lokális mozgás, fénysebességű forgás, anyag és antianyag, elektron, pozitron, neutrínó, kvarkok

Elem_5: Általános relativitáselmélet: Elv: a tér torzulása a gravitációs erő forrása

Dia 6:  Gumimatrac

Elem_6: Kvantummechanika, kvantum: a fénysebességű forgás impulzusnyomatéka

Elem_7: Az ősrobbanás:  Georges Lemaître (ősatom), Fred Hoyle (steady-state univerzum),  Edwin Hubble (galaxisok vörös eltolódása: táguló univerzum). Mi vagyunk a világ közepe?

Dia_7: kocka alakú dobozok

Kínai eredetmítosz: „Az ég naponta három méterrel emelkedett magasabbra, a föld három méterrel vastagodott. Így folytatódott ez 18 ezer éven át, míg az ég elérte a legnagyobb magasságot, és a föld a legnagyobb mélységet”

Polinéz:  Az istenek seregéért van az éj,

Az emberekért van a napvilág.

Az éjben csak az istenek születnek kitágulása óta ennek a világnak…

Nagyobbodott Tumu-nui, nagyobbodott Papa’raharaha, nagyobbodott (az isteneknek és az embereknek) háza, nagyobbodott az égnek alja.

Nőttön-nőtt az ég, szélesbedett az ég, és vele Havai’i földjének cölöpei.

Mi az a hajtóerő, ami az univerzum tágulását előidézi?

Elem_8: Termodinamika. Elv: entrópia. Változás iránya: a valószínűbb (többféleképpen megvalósuló) állapot felé történik

Dia_8: szita és dobókockák

Dia_9: gyöngyök

Kezdeti forró átmenet szakasza: Az óriási hőmérsékleten az ütközések szétverik az atomokat , az atommagokat sőt azok alkatrészeit a nukleonokat is. Ez a kvarkok és gluonok kaotikus plazma állapota?

Dia_10: Piruett a zsúfolt jégen

Szerintem: kaotikus fénysebességű lüktetés. Nincs idő a forgások kialakulására a túl gyors lüktetés miatt. A forgási frekvenciának is van felső határa! Evolúció: a rendezetlen lüktetésből alakul ki a rendezett forgások, azaz a kvantumok világa. Nukleonok, atommagok, atomok, égitestek, galaktikák

Polinéz: Tane üdvözölte Ra’i-tupu’át és így szólott hozzá: „Kelj fel Ra’i-tupu’a és tedd, ami dolgod! Tétessen a helyére a kavargó ég, hogy rend legyen és gyönyörűség!”

Ra’i-tupu’a ekkor helyére tette a kavargó eget. Mint ahogyan a kézművesek rendezik a csónakok pallóit, úgy dolgozott Ra’i-tupu’a a kavargó égen.

Tane gondosan felmérte az egeknek űrét, egének palástját.  Ra’i-tupu’a azután helyére tette a Holdat és a Napot és a csillagokat a tengerkék égben alulról, miközben Ma-tohi rögzítette a helyükön a magasban.

A Nap járásának lassítása

Az anyag kialakulása plasztikusan jelenik meg az indiai mitológiában:

Indiai: „Az egyetemes anyag legfinomabb rezgéseiből létesült a felső kör; a középső kör átmenet volt a finom rezgésű anyag síkjai között; az alsó körben pedig az anyag legsűrűbb, ütköző, nehézkedő rezgései bontakoztak szét megszámolhatatlan alakzattá.”

Az őselem koncepciója is megjelenik az egyiptomi mitológiában:

Egyiptomi: „Kezdetben nem volt sem ég, sem föld, sem élők, sem holtak nem voltak, az alkotó és romboló elemek is dermedt tétlenségben nyugodtak Nun isten örvénylő mélyén. Nun volt az őselem, az ősvíz formájában létező istenlény. Az ő alkotórészeiből keletkezett a mindenség.”

A kínai mitológiában az ég és föld teljes egysége mutatkozik meg:

Kínai: „Kezdetben, amikor az ég és a föld még tojás alakú káosz volt, Pan Ku megszületett a tojásban, és itt élt tizennyolcezer esztendeig. És ekkor a Jang tiszta elemeiből megformálódott az ég, a Jin durvább elemeiből pedig a föld. Pan Ku a középpontban tartózkodott, és nap mint nap kilenc alkalommal alakult át: hol az ég, hol pedig a föld istene volt.”

Az egy-isten hit a kiindulópontja a teremtésnek (Visnu, Pan Ku, Nun, Apszi, Ta’aroa):

Ta’aroa benn nyugodott a burkában, az éjben, a legrégibb  időktől fogva.

Mint egy tojás olyan volt a burok, forgott az űrben, nem volt ég, sem föld, sem hold, sem csillagok. Az éj volt csak egyedül, a végtelen éj, az áthatolhatatlan sötétség…

Hogy alakul ki a föld, ami Japánban a szigeteket jelentette a káoszból:

Japán: „Izanagi és Izanami letekintettek a Menny Lebegő Hídjáról, és azt fürkészték, van-e föld valahol a híd alatt. Csillogó drágakőből hatalmas lándzsát készítettek, a fegyvert lehajították, és rábukkantak a tengerre. Ezután kiemelték a lándzsát a káoszból, a káosz cseppenként aláhullott, megszilárdult, és így keletkezett Onokoro-Jima, a Megdermedt Sziget.”

A tibeti mitológiát a filozófia megfogalmazás tökéletessége jellemzi:

Tibeti: „Kezdetben semmi sem létezett, sem tér, sem idő, sem valóság, sem jel, sem lét, sem nemlét. Ebből keletkezett minden, ami látható és tapintható.

Az első lény varázslatos átalakulási képességgel született. Megnevezte magát: "A Keletkező Világ Ura, Szent Győzedelmeskedő". És boldog volt, mert hatalma mindenre kiterjedt.”

Az ősrobbanás elmélet szerint az első másodpercben több minden történt, mint a rákövetkező 13,7 milliárd év alatt! Fokozatosan alakultak ki a nukleonok, majd az atommagok és jóval később az atomok.

Görög időfogalmak: kronosz és kairosz. Fizika: mérési utasítás. Hogyan mérjük az időt a „forró” univerzumban?  Eseménysűrűséggel. Ha az események exponenciális sebességgel változnak, akkor a logaritmikus idő adja a jó skálát! Ebben a Planck-idő 10^-43s -43 lesz, az egy másodperc  lesz a nulla, mai korunk 17,635. Az ősrobbanás logikai ellentmondás! Mi volt az ősrobbanás előtt? De az „előtt” idő fogalom, aminek nincs értelme, ha nincs univerzum. Ez a fizikai gondolkozás csapdája. Ha a világ keletkezését magyarázni akarjuk, akkor ki kell lépni a szűk fizikai gondolkozás kereteiből. Az anyagi valóságból nyert fogalmaink nem magyarázhatják az anyagi világ keletkezését, csupán az evolúcióját.

Az ókori gondolkozás titka: a világot – beleértve a szellemi és anyagi világot is – annak egységében látták. Az ég és a föld, az isten és az ember, az ideák és a dolgok világa egységében jelenik meg.

Az ideák létrejötte a tibeti mitológiában:

Tibeti: Ekkor a négy évszak még nem vált el egymástól, a nap, a hold, a bolygók és a csillagképek alig mozdultak, a mennydörgés, a villámlás, az eső, a jég, a fagy sem követték az évszakok változásait. A földnek nem volt ura, az erdők, a növények maguktól nőttek és szaporodtak. A kövek és a hegyek már létrejöttek, de még nem mozdultak, és a földrengés is ismeretlen volt. A föld aranyból volt. A folyók is megvoltak már, de még nem indultak el a tenger felé. Madarak és vadak is éltek az erdőkben, de még senki sem vadászott rájuk. Istenek is léteztek, de még nem hallgatták meg a könyörgéseket, és nem uralkodtak ég és föld felett. Létrejöttek a démonok is, de még nem kezdhették el romboló munkájukat. Voltak betegségek, de még nem okoztak kínt és fájdalmat. Volt már táplálék, de még senki nem fogyasztotta. A boldogság is létezett, de nem volt, aki felfogja. A nappal nem különbözött az éjszakától.

Hogyan alkot a szobrász? Az ideák teremtése megelőzi a dolgok teremtését. A platoni ideák évezredekkel Platon előtt léteztek, Platon csak összefoglalta az ókori bölcseletet. Arisztotelész a választó vonal, amikor megszűnik az egységben gondolkozás, szétválik az ideák és a dolgok világa, leválik az anyagi természetről való gondolkozás a szellemiről. Ez a fragmentált modern gondolkozás kezdete

Mi a teremtés:  nyugvó gondolat: ideák, megrezdült gondolat (megnevezés):  dolgok

Indiai : A Világéjszaka sötét, mindent elborító, mozdulatlan tengerének színén összecsavarodva nyugodott Ananta, a Végtelenség Kígyója, s rajta álomba merülve pihent Visnu, a mindenség létesítője és fenntartója, az egyetlen hatalom. Bensejében a világ egész tartalma mint nyugvó gondolat derengett, rajta kívül nem volt élet, nem mozdult semmi. Álmában egyszerre megrezdült benne a gondolat, és Visnu felébredt. Kinyitotta szemét, és látott. Abban a szempillantásban megindult a mozgás az odáig nyugvó ősanyagban. Visnu létesítő akarata kisarjadt, és köldökéből egy lótusz nőtt elő. A lótusz széttárta szirmait, és íme, a lótusz kelyhében ült Brahmá, az Egynek Teremtő Ereje.

Mezopotámiai:  Midőn fönn az ég nevetlen s alant a föld szintazonképp;

Apszu, az ős-kezdet, minden dolgok teremtője-atyja

s Mummu-Tiámat ősanyánk még vizeikkel egybemosódtak;

nem volt szárazföld se, láp se, s egyike sem az isteneknek;

név nélkül szunnyadott a sors is, betöltetlen várt a végzet

Maja: Elmélkedtek (az istenek), és íme, megvilágosodtak, megjelent az Ősfényhajnal, és terveikben megjelent az ember.

Ennek utána elgondolták a teremtést, elgondolták a fák és folyondárok növekedését, az élet születését és az ember alkotását és a sötétségben és fénytelen éjszakában ekképpen szerezte mindezt Égszíve, az, akit Hurakánnak mondanak...

Miképpen legyen élet, és miképpen jöjjön létre világosság? Kinek kell gondoskodnia táplálékról és betévő falatról?

- Jöjjön immár, és legyen! Népesüljön be az üresség!

Az ég teremtése megelőzi a földét, a világosság teremtése megelőzi a Napét:

Mózes: 1. Kezdetben teremté Isten az eget és a földet.

2. A föld pedig kietlen és puszta vala, és setétség vala a mélység színén, és az Isten Lelke lebeg vala a vizek felett.
3. És monda Isten: Legyen világosság: és lőn világosság.
4. És látá Isten, hogy jó a világosság; és elválasztá Isten a világosságot a setétségtől.
5. És nevezé Isten a világosságot nappalnak, és a setétséget nevezé éjszakának: és lőn este és lőn reggel, első nap.

Ősrobbanás elmélet: 380 ezer év után jöttek létre az atomok, ezáltal lett átlátható, azaz világos az univerzum. Ennek nyoma a mikrohullámú háttérsugárzás. A csillagok és galaxisok képződése csak jóval később jöttek létre.

Mózes: 14. És monda Isten: Legyenek világító testek az ég mennyezetén, hogy elválasszák a nappalt az éjszakától, és legyenek jelek, és meghatározói ünnepeknek, napoknak és esztendőknek.

15. És legyenek világítókul az ég mennyezetén hogy világítsanak a földre. És úgy lőn.
16. Teremté tehát Isten a két nagy világító testet, a nagyobbik világító testet, hogy uralkodjék nappal és a kisebbik világítótestet, hogy uralkodjék éjjel; és a csillagokat.
17. És helyezteté Isten azokat az ég mennyezetére, hogy világítsanak a földre;
18. És hogy uralkodjanak a nappalon és az éjszakán, és elválasszák a világosságot a setétségtől. És látá Isten, hogy jó.
19. És lőn este és lőn reggel, negyedik nap.

A blog további írásait összefoglaló bejegyzés: "Paradigmaváltás a fizikában." 

Miért relativisztikusak a fizikai törvények?

A modern fizika törvényeit azért nehéz befogadni, mert következtetései gyakran nem követik gondolkozásunk megszokott menetét.  Erre példa a relativitáselmélet és a kvantummechanika világa. Itt most bonyolult matematikai formulák felhasználása nélkül kívánom bemutatni, hogyan lehet köznapi logikánk segítségével érthetővé tenni, az egyébként a józanésszel ellentmondani látszó fizikai törvényeket is.

Mi következik az univerzum létezéséből?

Kiindulópontunk egy olyan állítás, amit aligha von kétségbe bárki is: az univerzum létezik! Ebből az egyszerű állításból szinte az egész relativitáselmélet levezethető! Az ősrobbanás elmélete szerint az univerzum már régóta, hozzávetőleg 13,7 milliárd éve létezik, és nem mutat semmi jel arra, hogy hirtelen fel akarna robbanni, vagy eltűnni. Univerzumunk tehát stabilis képződmény. De lehetséges lenne ez, ha nem lenne határa a kölcsönhatások sebességének, ha az univerzum bármely pontja késleltetés nélkül megváltoztathatna valamit az univerzum egy másik pontján?  Gondoljuk végig, hogy mi is történne ilyenkor? Természetesen ekkor minden hatásra késleltetés nélkül jönne a válasz. A válaszra pedig azonnal viszontválasz születne. Az egyidejűleg jelentkező végtelen sok hatás és viszonthatás összegeződne, aminek eredménye vagy robbanás, vagy egymás kölcsönös megsemmisítése lenne. Az univerzum tehát nem lehetne olyan stabilis, ami jellemzi az elmúlt néhány milliárd évet. Az univerzum létezése ezért megköveteli, hogy a hatást késleltetve kövesse a válasz, azaz a kölcsönhatások sebessége véges legyen.

A kölcsönhatások határsebessége

Két olyan távolba ható kölcsönhatás van, ahol gyakorlati jelentősége van a kölcsönhatások véges sebességének, az egyik a gravitáció, a másik az elektromágneses kölcsönhatás. Elképzelhető, hogy eltérő a sebessége a két kölcsönhatásnak?  A töltéssel rendelkező fizikai objektumok, például az elemi részecskék tömeggel is rendelkeznek. Ha eltérne egymástól a két kölcsönhatás sebessége, akkor szétválna egymástól a két hatás. Például már éreznénk egy objektum gravitációs vonzását, de elektromos hatása még nem érkezne meg. Ez a megfigyelő számára kettéválasztaná a fizikai objektumot: az egyik már létezne a számára, a másik még nem. Ez szétszakítaná fizikai világunkat, ezért csak olyan lehet a világunk, amelyben a két nevezett kölcsönhatás sebessége azonos. Ezt szemléltetendő képzeljük el, hogy egy a Napnál sokmilliószor nagyobb és fényesebb csillag száguldana el naprendszerünk külső határán, úgy egyfényévnyi távolságban. Ennek hatására áradás indulna meg a tengerekben és az éjszaka is olyan világos lenne, mint a nappal. De mikor vennénk ezt észre? Nem akkor, amikor a legközelebb lenne ez a csillag, hanem csak egy évvel később. A gravitációs és a fényhatás viszont egyszerre érkezne el hozzánk. Evvel logikai úton eljutottunk a relativitáselmélet fontos törvényéhez, mely szerint minden kölcsönhatás a fény c sebességével terjed.

Mi az inercia rendszer?

A relativitáselmélet törvényei azért vannak távol mindennapjainktól, mert csak olyan sebességi tartományban van jelentős hatásuk, amikor már a fény irdatlan sebességéhez közel járunk. Ismert hasonlat, hogy a fény egyetlen másodperc alatt hét és félszer lenne képes körüljárni a Földet. Képzeljünk most magunk elé egy másik világot, ahol sokkal alacsonyabb a határsebesség, legyen mondjuk 100 km/óra. Szálljunk fel egy vonatra, amelyik éppen 99 km/óra sebességgel száguld. Ha a vonat sebessége állandó és nem láthatjuk a külvilágot és nem halljuk a kerekek zakatolását sem, akkor nem is tudjuk, hogy állunk-e vagy nagy sebességgel haladunk. Ekkor semmi nem változik a vonaton, nem fog más ütemben mozogni óránk mutatója sem. Az ilyen rendszert nevezi a mechanika inercia rendszernek. Észrevesszük azonban, ha a vonat gyorsul, vagy lassul, mert akkor a tehetetlenség miatt hátra eshetünk, vagy előre, ha nem kapaszkodunk.

A sebességek relativisztikus összegzési szabálya

Ezen az állandó sebességű vonaton tegyünk néhány lépést a vonat haladási irányában 5 km/óra sebességgel és menjünk át a 10 m hosszú szerelvény másik végébe. A vonaton kívüli pontokhoz képest mekkora sebességgel fogok mozogni? Ez nem lehet 99+5 = 104 km/óra, mert ez már meghaladná a határsebességet, a tényleges sebesség ezért még 100 km/óra alatt fog maradni. Evvel eljutottunk a relativitáselmélet egy meglepő törvényéhez: a sebességek nem adódnak össze a szokott módon. Szemléltessük ezt egy gondolatkísérlettel.  Legyen valaki a sínek mellett, aki egészen közelről egy fényjelet ad le, amikor a szerelvény egyik végében vagyok. A jel olyan közelről érkezzen, hogy ne kelljen számításba venni, hogy mennyi idő alatt jut el hozzám. Abban a pillanatban, amikor a szerelvény másik végébe értem én adok le egy fényjelet valakinek, aki szintén a sín mellett áll. A két ember órája alapján meghatározzák az időt, majd evvel osztva a távolságukat megkapják, hogy mekkora volt hozzájuk képest az én sebességem. Ez nem lehet 100 km/óránál több, mert ha így lenne, akkor sikerülne a két ember között az információt a határsebességnél gyorsabban továbbítani.

A távolság relativisztikus csökkenése: Lorentz kontrakció

Hogyan lehet, hogy hiába tettem meg 10 métert 5 km/óra sebességgel a vonathoz képest mégsem léphettem át a sebességhatárt? Ennek oka, hogy a vonatot kívülről nézve a szerelvény hossza összezsugorodik, tehát kívülről nézve én nem 10 métert tettem meg, hanem rövidebbet. Itt hangsúlyozni kell, hogy ez a rövidülés, amit Lorentz kontrakciónak hívnak a külső és a vonathoz képest 99 km/óra sebességgel elmaradó megfigyelő rendszerére vonatkozik. Hasonlóan, ha a sínek mellett 10 méterenként oszlopok vannak, akkor a vonatból megfigyelve ezek távolsága kisebb lesz. Tehát a zsugorodás relatív, attól függ, hogy melyik inercia rendszerből határozzuk meg egy másik inercia rendszerben lévő távolságot.

Relativisztikus tömegnövekedés

De nem csak a távolság és a sebesség függ az inercia rendszer relatív sebességétől, hanem a tömeg is. Ha valaki 10 méterre képes eldobni egy súlygolyót, de mi a dobást a vonat ablakából figyeljük meg, akkor úgy látjuk, hogy a dobás hossza rövidebb. Ezt a Newton törvény alapján úgy értelmezzük, hogy a dobó csak kisebb gyorsulást adott a golyónak, mert a ténylegesnél nagyobb a tömege. Így jutunk el a tömegnövekedés törvényéhez. Tehát minden relatív, a távolság, a sebesség és a tömeg is, csak egy dolog van, ami minden inercia rendszerben azonos, ez pedig a határsebesség!

A fénysebességű mozgás hatása

De mi történne a 100 km/óra sebességű vonaton? Itt bármekkora sebességgel mozognék a vonaton kívülről nézve az én sebességem mindig 100 km/óra maradna, ami azt jelentené, hogy ekkor a szerelvény hossza nulla lenne, és így hiába mennék át a szerelvény másik végébe nem növekedne tovább a teljes sebesség. A nulla hossz pedig azt jelentené, hogy az eldobott súlygolyó nem repülne el egy parányit sem, mert a tömege végtelenül nagyra növekedne. A tömegnövekedési szabály persze a vonatra is vonatkozik, ezért a vonat sem érhetné el a határsebességet. Mégis van valami, ami képes határsebességgel mozogni, ez pedig maga a fény, illetve annak kvantuma a foton. Ez viszont megköveteli, hogy a foton tömege nulla legyen. Úgy mondhatjuk, hogy a nullatömegű objektumok privilégiuma, hogy fénysebességgel terjedjenek. De nem csak privilégiumuk, hanem „kötelezettségük” is, nullatömegű objektumokról csak akkor van értelme beszélni, ha fénysebességgel haladnak, ettől válnak "anyaggá" és ez megfigyelhetőségük kritériuma. A tömeg és energia ekvivalenciája E = m.c² a modern fizika egyik legfontosabb törvénye, ez minden fizikai objektumra, így a fotonokra is érvényes. Tehát a fotonoknak is van tömegük, de ez nem „nyugalmi” tömeg, ez a fénysebességű mozgásukból fakad. A fénysebességű mozgás azáltal, hogy végtelenszer megnöveli a nulla nyugalmi tömeget, létrehozhat valami végeset, amit mozgási tömegnek nevezhetünk. A matematika ezt úgy írja le, hogy a határértékben végtelenül kis mennyiséget végtelenhez tartó számmal szorozva véges mennyiséghez jutunk:

akkor is, ha X végtelenhez tartó mennyiség.

Az idő dilatáció és az ikerparadoxon

De nem beszéltünk még a relativitáselmélet legnehezebben megérthető jelenségéről, az idő dilatációról. Ha a vonatunk 99 kilométert tesz meg egy óra alatt, akkor a sebessége 99 km/óra. De hogyan ítéli ezt meg a vonaton utazó? Számára a távolság kontrakciója miatt úgy tűnik, hogy csak rövidebb utat tett meg, ezért ha ezt a rövidebb távolságot osztja el a sebességgel, akkor rövidebb menetidőt állapít meg, azaz számára az idő lassabban telik. Ez az idő dilatáció. A jelenség sajátos következménye az ikerparadoxon. Az ikrek egyike világkörüli útra indul, és nagy utakat tesz meg a fényét megközelítő sebességgel, majd évek múltán visszatér. Ez alatt ikertestvére megöregszik, míg ő fiatal marad. Ismételjük meg ezt a 100 km/óra határsebességű világban. Induláskor hasonlítsuk össze óránkat valakivel, majd utazzunk el a 99 km/óra sebességű vonattal, majd utazásunk végeztével térjünk vissza a kiindulópontra. A mi óránk ekkor kevesebbet fog mutatni. Ez látszólag ellentétes avval a megállapítással, hogy az állandó sebességű vonaton semmi nem változik meg az állóhoz képest, így az óra is ugyanolyan ütemben jár. De ebből a gondolatmenetből épp a lényeg hiányzik: csak úgy tudunk nagy sebességgel utazni, ha előzőleg felgyorsult a vonat, majd visszafele lelassult. Amikor nem vagyunk inercia rendszerben már más szabályok érvényesek a tehetetlenségi erő megjelenése miatt. Ez pedig már az általános relativitáselmélet területe, ahol a gravitáció forrása a tehetetlenségi erő.  A valódi világban, ahol a fénysebességet kell megközelíteni, igen intenzív gyorsulásra illetve lassulásra van szükség, amelyik az óriási tehetetlenségi erő miatt lassítani fogja óránk járását, más szóval az eltelt időt. Megtudjuk ebből, hogy hol kell keresni az örökfiatalság titkát: az állandó gyorsulásban.

Hogyan jön létre a tömeg?

A fény kvantumáról, a fotonról megállapítottuk, hogy a fénysebességű mozgás révén energiára, azaz mozgási tömegre tesz szert. Vajon nem lehet, hogy minden fizikai objektum, az összes elemi részecske is, valamilyen fénysebességű mozgásnak köszönheti tömegét?  Induljunk ki a foton tulajdonságaiból és nézzük meg, hogyan vihetjük át annak fizikai jellemzőit az elemi részecskére. A foton energiája frekvenciájától függ, viszont bármekkora is a frekvencia az impulzusnyomaték mindíg hajszálra azonos, amit a ℏ Planck állandó ad meg. Ugyanez a Planck állandó köti össze a frekvenciát az energiával az E = h.ν = ℏ.ω szabályon keresztül. A fotonnak impulzusa is van p = h.ν/c értékben. Ez viszont közvetlen kapcsolatot jelent az energia és az impulzus között: E = p.c. Tehát a fénysebességet úgy is értelmezhetjük, hogy ez az energiát és impulzust összekötő arányossági tényező.

Honnan származik a foton impulzusnyomatéka?

Impulzusnyomaték létezése két dolgot kíván meg: forgást és forgási sugarat. Az ω frekvenciát értelmezhetjük a forgás szögsebességének, és ha a forgás kerületi sebessége c, akkor a sugár is értelmet nyer r = c/ω. Mivel az impulzusnyomaték a szögsebességgel és az objektum sugarával arányos, így már arra a kérdésre is választ kapunk, hogy miért azonos ez a nyomaték bármekkora is legyen az ω szögsebesség. A foton forgása mellett fénysebességgel terjed is, azaz mozgását mint egy  fénysebességű forgás és haladás kombinációját adhatjuk meg.

Az elemi részecskék impulzusnyomatéka

Az elemi részecskék, mint például az elektron és a proton (tehát a fermionok) szintén rendelkeznek impulzusnyomatékkal, aminek értéke ℏ/2, azaz fele akkora, mint a fotoné. A fotonnal szemben viszont rendelkeznek nyugalmi tömeggel és nem mozoghatnak fénysebességgel. Ahogy a fotonnál kétféle fénysebességű mozgás (forgás plusz haladás) hozza létre a mozgási tömeget, így az elemi részecskéknél is lehet kétféle mozgás, ami végül létrehozza a nyugalmi tömeget, de mivel itt a haladás sebessége nem lehet c, így kézenfekvő a feltételezés, hogy mindkét mozgás forgásként valósul meg. Az elemi részecskék nem rendelkeznek kitüntetett iránnyal, azaz forgásuk csak gömbszimmetrikus lehet. A kétféle forgás együttese ezt a kritériumot is teljesíti. Minden forgás centrifugális erőt kelt, a forgást ezért valamilyen centripetális erőnek ellensúlyozni kell. Ezt biztosítja a korábbi bejegyzésekben már tárgyalt erős gravitáció, ami a fénysebességű forgások által létrehozott extrém mértékű tértorzulás által jön létre (lásd az általános relativitáselmélet alapelvét). Fermionok esetén az erős gravitációnak két különböző forgással kell egyensúlyt tartani, ezért lesz az elemi részecskék impulzusnyomatéka fele akkora, mint amekkorával a foton rendelkezik.

A speciális relativitáselmélet energiaegyenlete

Értelmezzük úgy a speciális relativitás alapelvét, hogy az valamennyi részecske esetén az energia és az impulzus arányosságát fejezi ki, ahol az arányossági tényező a c fénysebesség: E = p.c.

A részecske impulzusának két összetevője van: p₀ fejezi ki a sajátmozgást, p₁ a tömeggel rendelkező objektum mozgását a külső térben, azaz

p = p₁ + p₀

Itt a félkövér betű fejezi ki, hogy az impulzus vektoriális mennyiség szemben az impulzus nagyságát megadó skaláris kifejezéssel.  Képezzük az energia és impulzus kapcsolatának négyzetét:

A gyors sajátforgások hatásának csak a várható értékét figyelhetjük meg. A gömbszimmetrikus mozgások miatt <p₀> = 0, így a négyzetre emeléskor a kereszttag eltűnik:

Ez pontosan megfelel a relativisztikus energiaegyenletnek, mely szerint

A két egyenlet azonossága miatt p₀ = m₀.c, ami annak felel meg, hogy az m₀ nyugalmi tömeg valójában a fénysebességű mozgás által tesz szert impulzusra. Evvel kimutattuk, hogy a speciális relativitáselmélet energiaegyenlete az energia és az impulzus arányosságára vezethető vissza. A törvényt eredetileg makroszkopikus testekre állapították meg, de ennek azaz alapja, hogy valamennyi elemi részecske energiája ugyanúgy épül fel a kinetikus és a nyugalmi energiát leíró tagokból.

Összefoglalás

A stabilis univerzum létezése megköveteli, hogy minden kölcsönhatásnak véges legyen a határsebessége, ami a fénysebesség, és ebből következnek a relativitáselmélet törvényei is. A fénysebességű mozgás hozza létre a tömeggel rendelkező anyagot. A határsebesség köti össze az energiát az impulzussal, és ez az összefüggés az alapja a relativisztikus energiaegyenletnek.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Az írás második részében ismertetem a ma széles körben elfogadott ősrobbanás elmélet alapjait és kiegészítem a részecskék fénysebességű mozgásából fakadó következményekkel. Az ősrobbanás tükrözi a modern ember gondolkodásmódját, amely a tudományokra alapozott hitre épül. Az ókori kozmológiát a fantázia szabad szárnyalása jellemzi, míg napjainkét a különböző tudományok eredményeinek összevetése. Megjelenik benne az általános relativitáselmélet koncepciója a gravitációról, a részecske fizika törvényei, a kvantumelméletek összefonódása és a termodinamika is. Az elméleti megfontolásokat pedig a csillagászati megfigyelések támasztják alá. Jelentős sikereket mutathat fel az ősrobbanás elmélete, de legalább ennyi kérdésre nem tud válaszolni. Ez utóbbira néhány esetben a fénysebességű forgások koncepciója adhat útmutatást. A legfőbb megválaszolatlan kérdés azonban fennmarad: hogyan lehet átlépni a lét és a nem-lét határát, vagy más fogalmazásban miért következett be egyáltalán az ősrobbanás? Erre a kérdésre a tudomány nem is adhat igazi választ! Az ősrobbanás elméletére ezért úgy tekinthetünk mint napjaink mitológiájára.

Az elmélet születése

Talán nem is véletlen, hogy az elmélet alapjait egy katolikus pap, Georges Lemaître dolgozta ki. Kiinduláspontja Einstein általános relativitáselmélete volt, amivel a spirális galaxisok távolodását kísérelte meg leírni. Már 1927-ben felvetette az „ősatom” koncepcióját feltételezve, hogy a galaxisok távolodása az univerzum alapjelensége, amit visszavetítve a messze múltba, kellett lenni egy olyan kezdő pillanatnak, amikor az összes galaxis egyetlen matematikai pont volt, amelyben az egész univerzum összes energiája benne foglaltatott. Meghökkentő állítás, ha arra gondolunk, hogy milyen óriási energia van a Napban és a Nap csak egy szerény csillag a Tejútrendszer milliárd csillagja közül, és a galaxisok száma is eléri a milliárdot! Szabad-e ilyen messzire extrapolálni, mi a garancia arra, hogy a fizika törvényei változatlanok ilyen extrém körülmények között, amikor a nyomás, az anyagsűrűség és a hőmérséklet elképesztő mértékben megemelkedik? A fizikusok többsége ezért sokáig inkább Fred Hoyle hipotézisét fogadta el, amelyben állandó állapotú (steady state) univerzumot tételezett fel, szerinte a tágulás tömeget hoz létre és így az univerzum tömegsűrűsége és hőmérséklete mindig állandó marad. 

Hubble tágulási törvénye

A tágulási törvényre Edwin Hubble talált bizonyítékot, amikor 1929-ben a galaxisok vöröseltolódása alapján kimutatta, hogy a távolodás sebessége arányosan növekszik a távolsággal, tehát a közeli galaxisok lassan, a távolaik gyorsan távolodnak. (A vöröseltolódás Doppler-jelenség: ahogy a távolodó vonat hangja mélyül, úgy csökken az atomok által kibocsátott fény hullámhossza is, azaz a látható tartományban a kék szín a vörös felé tolódik el).

Itt álljunk meg egy pillanatra, hogy értelmezzük az univerzum tágulását. A térnek csak ott van értelme ahol anyag is van (az anyag fogalmába értsük bele a fényt is!). Tehát az univerzum nem a tőle függetlenül létező térben tágul, hanem magának a térnek tágulásáról kell beszélni. Képzeljünk magunk elé egy háromdimenziós rácsot, amelyet egyforma kockák alkotnak. Ez reprezentálja a teret, amelyben a galaxisok elhelyezkednek. Minden egyes kocka azonos sebességgel tágul, emiatt minél távolabb van két kocka, amely magában foglal egy-egy galaxist, annál gyorsabban fog a közöttük lévő távolság növekedni. A tágulásnak nem kell ezért, hogy legyen valamilyen centruma (bár lehet), az univerzum bármely pontjában ugyanaz a tágulási szabály érvényesül. Az egyes kockákban a galaxisok mozoghatnak, ahogy a bolygók is keringenek a napjuk körül, vagy a csillagok mozognak a galaxisban, vagy a galaxisok is vándorolnak egymáshoz képest. Ha közel van a galaxis, akkor a saját mozgás lehet gyorsabb is, mint a „kockák” tágulása. Példa rá a közeli Androméda köd, amelyik közeledik a Tejútrendszer felé. Viszont a távoli nagysebességű galaxisoknál a saját mozgás sebessége kicsi a táguláshoz képest, ezért ezekre a Hubble-törvény már pontosan érvényesül. A kockák alakja azonban nem tökéletes, eltérhetnek egymástól az egyes oldalak. Ez a makro torzulás hozza létre a gravitációt az általános relativitáselmélet szerint. De van számtalan apró torzulás is a kockákon belül, amit a részecskék fénysebességű forgása hoz létre, ez a részecske sajátforgását stabilizáló erős gravitáció. A sok-sok apró mikro torzulás – azaz részecske – száma határozza meg, hogy mekkora az egyes kockák makro torzulása, azaz a szokásos gravitáció.

Az ősi forró univerzum

Az ősrobbanás elméletével lépésről-lépésre ismerkedjünk meg. A kezdeti rendkívül forró és sűrű állapot a tágulás miatt hűlni kezd. Ez a termodinamikából következik. Hozzá rendelhetünk az univerzumhoz entrópiát is, amelyik növekedni fog a hőmérséklet csökkenése miatt (lásd még az „Energia, entrópia és evolúció” című bejegyzést). A rendkívül intenzív hőmozgás szétveri az általunk ismert elemi objektumokat is, nincs ezért sem molekula, sem atom, sőt atommagok és az összetevő nukleonok (proton és neutron) sem létezhetnek. Ezt az állapotot úgy szokás leírni mint a kvarkok és gluonok rendezetlen plazmáját. (Evvel a felfogással viszont már vitatkoznék, mert minden eddigi kísérleti adat arra mutat, hogy a kvarkok csak a hadronokban (mezon és barion típusú elemi részecskék) létezhetnek, de önállóan nem figyelhetők meg. Mi a garancia arra, hogy éppen a rendkívül nagy termikus mozgások birodalma teszi lehetővé önálló megjelenésüket? Erre a kérdésre később még visszatérek.) A lehűlés tehát megnöveli az univerzum teljes entrópiáját, de ugyanakkor létrejönnek azok a lokális „szigetek”, ahol már életképesek maradnak az összetett objektumok, mint az atommagok, majd az atomok és a molekulák. Az entrópiát mint a rendezettség mértékét lehet definiálni, ebben az értelemben az összetett objektumok létezése éppen hogy csökkenti az entrópiát, mert az alkotóelemek többé nem mozoghatnak szabadon, egymástól függetlenül. Ezt úgy foghatjuk fel, hogy a tágulás, amelyik egyrészt az univerzum teljes entrópiáját növeli, másrészt megteremti annak feltételét, hogy lokális centrumokban csökkenjen az entrópia.  Tehát az univerzum evolúciójának motorja az univerzum tágulása!

A világosság elválik a sötétségtől

Koncentráljunk most az univerzum fejlődésének egy fontos mérföldkövére, amikor annyira lecsökkent a hőmozgás intenzitása, hogy létrejöhettek az atomok. Ez azt jelenti, hogy a negatív töltésű elektronokat már elegendő erő kötötte hozzá a pozitív töltésű atommaghoz, elsősorban a protonokhoz, hogy kialakuljon a stabilis hidrogén atom. Evvel létrejött a semleges töltésű atomok világa. Ennek két szempontból is óriási jelentősége van.  Amíg csak szabad protonokról beszélhetünk a közöttük lévő erős elektromos taszítás nem tette lehetővé, hogy a gravitáció csillaggá forrassza egybe a protonok tömegét. Az elektronok és protonok egymásra találása viszont kiiktatta az erős taszítást és megalakulhattak a csillagok és a galaxisok a gravitáció mindent átható vonzásán keresztül.  A csillagok nagy energia- és anyagsűrűsége ugyanakkor begyújtotta a nukleáris folyamatokat és ennek révén a csillagok fénye bevilágította a sötét univerzumot. Ugyanakkor a szabad töltések eltűnése elvette a szabadon mozgó töltések fényabszorbeáló hatását, más szóval kitisztult az univerzum, átláthatóvá vált. Tehát a sötétség és a világosság szétvált egymástól! Gondoljunk most az ókori mitológiákra, például Mózes teremtés könyvére: a világ teremtésének kezdetén szétválik a világosság és a sötétség!

A kozmikus mikrohullámú háttérsugárzás

Az ősrobbanás elmélete szerint ez a pillanat a kezdetektől számítva 380 ezer évvel később következett be; és az akkor kiszabadult sugárzás azóta is áthatja az egész univerzumot, ez a nevezetes kozmikus mikrohullámú háttérsugárzás (CMBR , azaz Cosmic Microwave Background Radiation). Ennek megértéséhez tegyünk egy kitérőt a fizika fekete test sugárzásának törvényéhez.  Amikor az acélt felizzítjuk, kezdetben a vörös szín jelenik meg, majd tovább hevítve világosodik ki a színe a kék és a fehér felé. Ugyanezt figyelhetjük meg, ha a kályhánkban a tűz kialszik és a hőmérséklet csökkenésével a parázs vörös fénye szökik szemünkbe. A termodinamika szerint minden test sugárzik melynek színét (frekvenciáját) a hőmérséklet szabja meg. Ha alacsony a hőmérséklet, ez akkor is igaz, de ekkor a kibocsátott sugárzás már a szemünk által nem látható, de kellemesen melegítő, infravörös tartományba esik. Minél alacsonyabb a hőmérséklet annál kisebb lesz a sugárzás frekvenciája, lemehet egészen a mikrohullámú tartományba, sőt az alá is. Ezt a jelenséget nevezi a fizika a fekete test sugárzási törvényének. A sugárzás frekvenciájának értékéből ezért meghatározhatjuk, hogy mekkora a hőmérséklete a kibocsátó testnek. Az univerzum egésze is pontosan követi ezt a szabályt, amiből meghatározták a hőmérsékletet, amit 2,73 K-nak találtak. A háttérsugárzás jelenségét George Gamow 1948-ban jósolta meg az ősrobbanás koncepciójából kiindulva, majd később, már 1965-ben, ezt a sugárzást Arno Penzias és Robert Woodrow Wilson fel is fedezte (1978-ban Nobel Díjban részesültek). Ez a felfedezés fordulópontot jelentett az ősrobbanás elméletében, amit azóta fogad el a fizikus társadalom többsége.

Az univerzum korának logaritmikus időskálája

Különböző, itt nem ismertetett csillagászati megfigyelések arra az eredményre vezettek, hogy az univerzum kora 13,7 milliárd év. De hogyan is mérjük az időt a fizikában? Mindig valamilyen periodikus jelenségből indulunk ki, mint a Föld forgása, vagy egy kristály rezgése, az inga lengése, vagy a sugárzás frekvenciája.  Az univerzum kezdetén azonban nem voltak csillagok és bolygók, nem voltak atomok és molekulák sem, tehát nem léteztek azok a fizikai folyamatok sem, ami alapján elvben az időt mérni lehetne. Az ősrobbanás elmélete a kezdetekben az univerzum rendkívül gyors változását tételezi fel, eszerint az első másodperc alatt nagyobb változás következett be, mint az utána következő 13,7 milliárd évben. Az ősrobbanás előtti időről pedig nem lehet beszélni, mert a fizikai átalakulásokat, eseményeket jellemző időnek csak akkor van értelme, ha a fizikai világ egyáltalán létezik. Szükség van ezért a maitól eltérő időfogalomra, ha jellemezni akarjuk az univerzum evolúcióját. Mivel a kezdetekben exponenciális sebességgel zajlottak le az átalakulási folyamatok, ezért logikusnak tűnik, ha a mostani idő logaritmusával jellemezzük az univerzum korát. Számoljuk ki tehát a 13,7 milliárd évet másodpercekbe és adjuk meg ennek logaritmusát: 17,635. Az egy másodperchez tartozó logaritmus a nulla. Az ősrobbanás elméletek a 10^-43s Planck időig tekintenek vissza, mint a kvantummechanikai bizonytalanság miatt értelmezhető időhöz, tehát -43 LI-hez (LI = logaritmikus idő). Ez a skála már szemléletesen mutatja, hogy a -43 és a mai kor 17,635 LI logaritmikus ideje között jóval több minden történt az első másodpercben (tehát a nulla pontig), mint utána összesen! Az univerzumot logaritmikus idővel jellemezve elkerüljük a logikai csapdát is, amikor megkérdezzük, hogy mi volt az ősrobbanás előtt? Nem volt „előtt”, mert nem volt idő sem: a logaritmikus skálán tovább léphetünk -43 LI-it megelőző tetszőlegesen nagy negatív számig anélkül, hogy annak hatványa elérné a nullát. A logaritmikus időskálán tehát nincs kezdete az univerzumnak csak egyre régebbi és régebbi korszakai. Nem kell tehát feltételezni, hogy egykoron a nem-létből megszületett a lét. Az ősrobbanás csupán egy gondolati absztrakció, amikor végtelenül messze nyúlunk vissza az idő folyamatában.

A logaritmikus idő előképének tekinthető a görög kairosz, amit megkülönböztetnek az események kronológiáját leíró kronosztól. A kairosz megszentelt idő, a nagy pillanatok hírnöke. Ennek megfelelően a logaritmikus idő az univerzum nagy fordulatait, átalakulását jellemzi.

A Planck idő

„A véges és végtelen az Univerzumban” című írásban már foglalkoztunk a Planck idő szemléltetésével, amit itt egy kissé eltérő gondolatmenet alapján vezetünk be. A korábbi írásban felvetettük a kérdést, hogy van-e elvi határa az elektromágneses sugárzás frekvenciájának, azaz energiájának és a hozzá tartozó mozgási tömegnek. Induljunk ki a részecskék, így a fotonok, saját energiájának számításából. Ehhez azt a munkát kell alapul venni, ami ahhoz szükséges, hogy a részecskét felépítsük, ha végtelenül távolról rakjuk össze. A fénysebességű forgás modellje alapján az extrém mértékben torzuló tér ℏ.c/r potenciális energiája (erős gravitáció) ellensúlyozza az m.c² = ℏ.ω kinetikus energiát fotonok esetén. Az m mozgási tömegnek azonban van gravitációs hatása is, ami ha az r sugarú hengerpaláston található, akkor a gravitációs sajátenergia G.m²/r lesz (G a gravitációs állandó). Bármely részecskénél és a földi körülmények között megfigyelhető gammasugárzásnál ez a tag 30-40 nagyságrenddel elmarad az erős gravitációtól, ezért mérhetetlenül kicsi a járuléka. Más a helyzet, ha azt a határt keressük, ami a lehető legnagyobb energiájú sugárzáshoz tartozik. Ekkor az m.c² energiában már együtt kell figyelembe venni az erős és a szokásos gravitáció hatását:

Rendezzük át az egyenletet:

Ennek megoldása:

A foton mozgási tömege, azaz energiája csak valós értékű lehet, ami megköveteli, hogy a négyzetgyök alatti kifejezés pozitív legyen, vagy nulla. Ez meghatározza a sugár legkisebb értékét, amely a Planck hossz legalább kétszerese:

Ez behatárolja a foton ω = c/r frekvenciáját, ami maximálisan a Planck idő reciprokának fele lehet:

A gammasugár frekvenciájának felső határa ezért 10⁴³ Hz körül lehet, ami 17 nagyságrenddel haladja meg a földi körülmények között észlelt, illetve gyorsítókban a proton ütközések által létrehozható sugárzás energiáját. Ez azt jelenti, hogy az univerzum Planck korszakának földi laboratóriumban való tanulmányozására nincs esély.

A fénysebességű forgások kialakulása az ősi univerzumban

A fénysebességű forgások modelljében a fotont mint egytengelyű, a fermionokat (elektron, proton stb) mint kéttengelyű forgást értelmeztük. Forgásról azonban csak úgy beszélhetünk, ha legalább egy fordulatra sor kerül, aminek tartama a periódus idő. Ez azt jelenti, hogy a -43 LI-vel jellemzett korszak előtt még a legnagyobb energiájú foton sem jöhetett létre, ennél is jóval később alakulhatott ki a proton, amihez legalább -25, vagy az elektron amihez -22 logaritmikus időegység szükséges.  Ebben az időtartományban azonban még nem maradhattak meg a részecskék, mert a rendkívül magas hőmérséklet rendkívül gyors ütemű ütközéseket hoz létre, a stabilitáshoz az szükséges, hogy az átlagos ütközési idő hosszabb legyen, mint az egyes részecskék sajátforgásának periódus ideje.

Ez fejeződik ki az ősrobbanás elmélete által meghatározott időkben, amit protonok és a hasonló tömegű barionok esetén 10^-4 másodpercnek, azaz -4 LI-nek becsülnek. Még jóval később kerülhet az elektron stabil pályára a proton körül, aminek kötési energiája kilenc nagyságrenddel kisebb a proton nyugalmi energiájánál. Ennek ideje az a bizonyos 380 ezer év, ami a logaritmikus egységben 13,079 LI-nek felel meg.

Az ősrobbanás elméletét úgy szokás ismertetni, hogy a korai korszakban (-4 LI előtt) az univerzumot a kvarkok és gluonok plazmája alkotta. Evvel nem értek egyet, mert a kvarkok kisebb tömege miatt eleve nem jöhettek hamarabb létre, mint a nehezebb barionok és mezonok, másrészt semmi bizonyíték nincs arra, hogy a kvarkok létezhetnének szabadon is. A fénysebességű forgásmodellnek az felel meg, hogy a részecskéket alkotó forgások kialakulása előtt rendezetlen, kaotikus lüktetés jellemezte az univerzumot. Ebben a rendezetlen mozgásban fokozatosan alakultak ki a rendezett forgások, először a legkeményebb gammasugarak, majd később a gyenge kölcsönhatás W és Z bozonjai, majd a hadronok (barionok és mezonok) családja és még később az elektron és a pozitron. Az elemi részecskék három generációja közül mindig a nagyobb tömegű objektumok képződtek először.  Ennek az elképzelésnek mitológiai előképe, ahogy a káosz óceánjából előbukkan földi világunk.

A fizikai erők elkülönülése

A részecskék Standard Modellje négy erőt ismer: az elemi részecskék erős és gyenge kölcsönhatását, az elektromágneses és a gravitációs kölcsönhatást. Az ősrobbanás kozmológiájában úgy képzelik el, hogy kezdetben nem váltak még szét az erőhatások, csak az univerzum lehűlése sorén kezdtek önálló életet. Ismét egy mitológiai előkép, melyben a négy erőt a négy szél képviseli. Leválik tehát az erős kölcsönhatásról az elektrogyenge, majd később ezen belül is szétválik az elektromágneses és a gyenge kölcsönhatás. Az erőhatások szétválását a különböző kvantum mező elméletek alapján értelmezik, melyben minden egyes kölcsönhatásnak megvan a maga közvetítő bozonja: az elektromágneses kölcsönhatást a foton, a gyengét a W és Z bozon, míg az erős kölcsönhatást a gluonok hozzák létre. Az egész elmélet gyenge pontja, hogy a gravitáció mezőelméletét nem sikerült megalkotni.

Az általam képviselt felfogás szerint van egy ötödik erő, az erős gravitáció, amely biztosítja a részecskék sajátforgását. Az univerzum evolúciójának első fázisátmenete ezért az erős és a szokásos gravitáció szétválása, amikor kiválnak a kezdeti rendezetlen mozgásokból a rendezett forgások. A forgások hozzák létre a részecskék saját impulzusmomentumát, a spint. Ennek nagysága egytengelyű forgásoknál a ℏ (bozonok), a kéttengelyű forgásoknál ℏ/2 (fermionok). Amikor ezek a forgások kialakulnak, akkor jelenik meg a forgások alapegysége a kvantum is. A kvantumosság tehát nem egy eleve létező természeti elv, hanem maga is az univerzum evolúciója során jön létre. Tehát az univerzum korai szakaszában nincs is kvantum, ennek megszületéséhez idő kell. Létezik hát egy kvantum előtti és egy kvantum utáni korszak. Ezt a kvantumot az erős gravitáció hozza létre a tér mikro deformációja által. A mikro deformációk (részecskék) sokasága hozza létre a tér makro deformációját, azaz a szokásos gravitációt. Ez a felfogás eltér a modern fizika jelenlegi szemléletmódjától, amelyben minden erőt a kvantumokhoz és a kölcsönhatást közvetítő bozonokhoz próbálnak hozzárendelni. Nem véletlen, hogy ezt az elvet nem lehetett a gravitációra kiterjeszteni, mert a gravitáció a tér alapvető szerkezeti tulajdonsága, amihez nincs szükség „közvetítőkre”. Közvetíteni csak az erős gravitáció által stabilizált mikro deformációk (részecskék) között kell, amikor leírjuk átalakulásukat (gyenge kölcsönhatás) és a közöttük feszülő erőket (erős és elektromágneses kölcsönhatás ).

 A tér kezdeti kaotikusan lüktető szakaszában a rendezett forgások könnyen egymásba alakulnak, ekkor még a kvarkokat összekötő erős kölcsönhatás nem válik szét a forgási módok egymásba alakulásáért felelős gyenge kölcsönhatástól.  Ez a szétválás akkor következik be, amikor a kéttengelyű forgások is stabilizálódnak. Az egytengelyű forgások két típusa, amikor a haladási irány a forgási tengellyel párhuzamos (foton) és amikor merőleges (W és Z bozon), akkor válik szét, amikor elég sok fordulat következik be, hogy jól definiált forgási tengelyről lehessen beszélni.

Az anyag dominanciája az antianyaggal szemben

A jelenlegi ősrobbanás elmélet gyenge pontja, hogy nem tud meggyőző magyarázatot adni a részecskevilág fölényére az antirészecskékkel szemben. Ennek oka, hogy a párképződés során minden részecske az antirészecske párjával együtt képződik. Viszont ez a pár előbb-utóbb annihilál és fotonokat hoz létre. Ennek feloldást úgy magyarázhatjuk, hogy a kaotikusan lüktető és forgásszimmetriával és ezáltal kvantummal nem rendelkező térből alakulnak ki rendezett és kvantumos  forgások. A kvantumok születési folyamata már nem követeli meg ugyanazokat a kiválasztási szabályokat, amit a mai hideg, konszolidált univerzumunkban megfigyelhetünk a gammasugárzás párkeltése során. Emiatt a protonok kialakulhattak antiproton párjuk, illetve az elektronok pozitron nélkül is. Például a fiatal univerzumban létrejöhettek  proton-elektron párok és ugyanakkora valószínűséggel képződhettek antiproton-pozitron párok is, de a kétféle pár tényleges száma a véletlen törvényszerűsége miatt már nem volt azonos. (ezt a szcenáriót alátámasztja, hogy az univerzumot a pozitív és negatív töltések egyensúlya jellemzi). Végül valamelyik pár a kettő közül többségbe került és ez a többség az annihilációs folyamatok lezajlása után már fennmaradt. Ezt a többséget nevezzük ma anyagnak, amely uralkodik az antianyag felett.

A korai univerzum felfúvódása

Végül térjünk ki az ősrobbanás egy sajátos jelenségére, az inflációra vagy felfúvódásra is.  Az univerzum kora 13,7 milliárd év, viszont egyes csillagászati megfigyelések szerint a mérete a vártnál nagyobb, úgy 30 milliárd fényév. Ez csak úgy lehet, ha egyes korszakokban a fénysebességet meghaladó növekedésre került sor. Jelenleg úgy becsülik, hogy -35 és -30 LI között lehetett az a korszak, amikor a térfogat akár 50 nagyságrenddel is megnövekedhetett. De hogyan egyeztethető ez össze a speciális relativitáselmélettel? Ennek magyarázatához gondoljuk végig miért szükségszerű, hogy minden kölcsönhatás sebessége véges legyen. Például az elektromágnesesség és a gravitáció egyaránt c sebességgel terjed. De mi történne, ha minden kölcsönhatás késleltetés nélkül éreztetné hatását? Például az egyik galaxis valamit megváltoztatna a másikon, akkor ennek hatása késleltetés nélkül visszahatna az elsőre. Ez újra hatna a másikra és a hatások végtelen sora jönne létre. Ha ezáltal valami növekedne az egyik helyen, akkor a növekedések egy végtelen sok tagból álló és egynél nagyobb kvóciensű mértani sor összegének felelne meg, ami viszont végtelen lenne és a galaxisok felrobbannának. Csökkentést okozó kölcsönhatás esetén pedig az egynél kisebb kvóciens miatt mindkét galaxis eltűnne. Stabilis univerzum ezért csak úgy alakulhat ki, ha minden kölcsönhatás sebessége véges és ez jelenik meg a hatások véges c határsebességében. Az univerzum felfúvódása nem mond ellent ennek az elvnek, csupán az univerzum jobban szétszakad egymással kölcsönhatásba nem kerülő téridő tartományokra. Ugyanis ha tőlünk egymillió év távolában felrobban egy szupernóva, akkor az nem befolyásolja világunkat, mert hatása csak millió év múlva jelenik meg. Ez azt jelenti, hogy a téridő két tartománya között nincs kölcsönhatás. A felfúvódás miatt viszont megnövekszik az a téridőt tartomány, amellyel nem állunk kölcsönhatásban. Az univerzum stabilitását ez a jelenség tehát megerősíti. De mi azaz erő, ami előidézte a felfúvódást? A kérdés megválaszolásával még adós az ősrobbanás elmélete..

Az ősrobbanás elméletéhez kapcsolható mitológiák: Az ősrobbanás és a teremtészmítoszok_III

Az ősrobbanás és a teremtésmítoszok

Ennek a bejegyzésnek kettős célja van. Egyrészt az ókori ember gondolkozásmódját hasonlítom össze a modern kor tudományokra alapozott felfogásával, másrészt az ősrobbanás mai elméletét vetem össze a részecskék fénysebességű mozgásából származtatható kozmológiával. 

Miért jutottak a különböző kultúrák és vallások a világ teremtésének, keletkezésének gondolatához? Minden ember megszületik, él és meghal, ugyanez vonatkozik valamennyi állatra és növényre is. Az egyes kultúrák emlékezetében él, hogy voltak előző kultúrák is, amelyek létrejöttek, virágoztak majd a semmibe tűntek. Ezért már az ókori ember is úgy gondolkozott, hogy ezen a világon semmi sem örök, mindennek megvan a maga küldetése, mindennek egyszer vége szakad. De ez együtt jár avval, hogy mindennek egyszer meg kellett születni, teremtődni. Ha ez minden létezőre igaz, akkor igaznak kell lenni az egész világra is.

Mózes első könyve

De mi is ez a világ? Van a mi világunk, a földi világ és ami fölöttünk van az égi világ. Ez a kettőség a kiindulópontja a legtöbb teremtésmítosznak is. Idézzünk mindjárt Mózes első könyvéből:

1. Kezdetben teremté Isten az eget és a földet.
2. A föld pedig kietlen és puszta vala, és setétség vala a mélység színén, és az Isten Lelke lebeg vala a vizek felett.
3. És mondá Isten: Legyen világosság: és lőn világosság.
4. És látá Isten, hogy jó a világosság; és elválasztá Isten a világosságot a setétségtől.
5. És nevezé Isten a világosságot nappalnak, és a setétséget nevezé éjszakának: és lőn este és lőn reggel, első nap.

Az ókori ember természetesen a „föld” alatt nem a Földet mint bolygót értette, hanem az egész világot, amiben élünk. De életünk nagymértékben attól függ, ami fentről az „égből” érkezik, onnan kapjuk az éltető napsugarat és az esőt, de félhetünk a viharoktól, erős szelektől és a villámoktól is. Ez a felső függés jelenik meg a korai istenképekben is, gondoljunk a görög-római vagy az egyiptomi mitológiákra. Az istenkép fejlettebb, letisztult formája, amikor kialakul az egy-isten, a mindenható a teremtő tisztelete.

Az első lépés tehát az égi és földi világ megteremtése, és itt nem véletlen a sorrend. A földi világ önmagában halott, a sötétség uralja. Fontos, hogy amire először van szükség az a világosság, amit ma úgy mondunk, hogy a fény. Ez megelőzi a Nap és Hold megteremtését is, amire csak a negyedik napon kerül sor:

14. És mondá Isten: Legyenek világító testek az ég mennyezetén, hogy elválasszák a nappalt az éjszakától, és legyenek jelek, és meghatározói ünnepeknek, napoknak és esztendőknek.

15. És legyenek világítókul az ég mennyezetén hogy világítsanak a földre. És úgy lőn.

16. Teremté tehát Isten a két nagy világító testet, a nagyobbik világító testet, hogy uralkodjék nappal és a kisebbik világítótestet, hogy uralkodjék éjjel; és a csillagokat.

17. És helyezteté Isten azokat az ég mennyezetére, hogy világítsanak a földre;

18. És hogy uralkodjanak a nappalon és az éjszakán, és elválasszák a világosságot a setétségtől. És látá Isten, hogy jó.

19. És lőn este és lőn reggel, negyedik nap.

Érdekes egyezés, amint látni fogjuk a modern kozmológiában is, hogy előbb jött létre a fény, mint a nap a hold és a csillagok! Az ősrobbanás elmélete előtt még úgy gondolhattuk, hogy milyen naiv a biblia megközelítés, ami a csillagok megszületése elé helyezi a fény és világosság megteremtését. Ez figyelmeztetés számunkra: ne becsüljük le az ősi népek gondolatvilágát. Modern elméleteink bizony gyakran tökéletlenek, amit a távoli jövőben fognak majd naivnak tartani.

Minden élet számára kiemelt fontosságú a víz, ezért kerül a víz „szétválasztása” már előre, a második napra. A sorrend tehát azt tükrözi, hogy mit tartott az ókor embere a legfontosabbnak. Mivel az ősi kultúrák a forró és száraz övezetekben alakultak ki, például Mezopotámiában és Egyiptomban, ezért a víz, az eső megjelenése előre kerül:

6. És mondá Isten: Legyen mennyezet a víz között, a mely elválassza a vizeket a vizektől.
7. Teremté tehát Isten a mennyezetet, és elválasztá a mennyezet alatt való vizeket, a mennyezet felett való vizektől.
8. És nevezé Isten a mennyezetet égnek: és lőn este, és lőn reggel, második nap.
9. És mondá Isten: Gyűljetek egybe az ég alatt való vizek egy helyre, hogy tessék meg a száraz. És úgy lőn.  
10. És nevezé Isten a szárazat földnek; az egybegyült vizeket pedig tengernek nevezé. És látá Isten, hogy jó.

Az égi víz, az eső, ami a felhőkből („mennyezet") származik hozta létre a tengereket. Megint egy érdekes egyezés, ahogy ma magyarázzuk a Föld forró korszakának lehűlése után a tengereinek kialakulását. Természetesen nincs arról szó, hogy a bibliai teremtéstörténet mindenben azonos lenne avval a sorrenddel, amit ma elképzelünk, de érdekes módon azért a sorrend sokszor a fontosság mellett kapcsolatba hozható a Föld és az élet evolúciójáról alkotott elképzeléseinkkel is.

A Korán

Az iszlám teremtéstörténet sok hasonlóságot mutat a bibliával, ennek illusztrálására olvassunk el néhány sort a Koránból is:

Allah megparancsolta a víz felett lebegő párának, emelkedjék a magasba. És két nap alatt megalkotta az eget. Ezután elválasztotta az eget a földtől, és létrehozta a hét eget és a hét földet.

Amikor Allah megalkotta a földeket, megparancsolta a szélnek, hogy kavarja fel a vizet. A víz megmozdult, és tajtékzott, magas hullámok tornyosultak, és sűrű pára képződött. Allah elrendelte a tajtéknak: szilárduljon meg,  és a tajték megszilárdult. Ebből alkotta meg két nap alatt a víz színén a földeket. Ekkor megparancsolta a hullámoknak: álljanak meg. A hullámok megmeredtek, és ezekből alkotta Allah a hegyeket.

Mezopotámiai mitológia

A víz különös fontossága jelenik meg a mezopotámiai teremtéstörténetben is, nézzük az első táblát:

Midőn fönn az ég nevetlen s alant a föld szintazonképp;

Apszu, az ős-kezdet, minden dolgok teremtője-atyja

s Mummu-Tiámat ősanyánk még vizeikkel egybemosódtak;

nem volt szárazföld se, láp se, s egyike sem az isteneknek;

név nélkül szunnyadott a sors is, betöltetlen várt a végzet

Az ég és a föld egymásutánisága szintén megjelenik, és kiemelt szerepet kap a víz. Az ókori gondolkozás másik jellegzetessége, hogy a „teremtés” voltaképp nem más mint „megnevezés”, erre utalt a Mózes könyvéből vett idézet 10. sora is! A mezopotámiai mitológiában az egymást követő és egymással harcoló istenek sora felel meg a teremtés egymást követő lépéseinek. Marduk születése kapcsolódik a Naphoz, képviseli a nappalok és éjszakák kettőségét, valamint a négy évszakot és a négy égtájat is. Idézzünk fel néhány sort még e korai költészet remekművéből:

Midőn Éa, nemzőatyja reánéz, örvend és ujjong - megdobog a szíve.

Tökéletesnek teremté őt, kétfejűnek; méltóságban mindenki mást felülmúl;

tagjai tündöklőbbek az elégnél;alig-felfoghatók, hozzá-nem-férhetőek.

Szeme négy és füle is négy vala, szájából lángos tűz csapott elő;

négy füllel fülelt, négy szemmel tekintett - mindent látott és mindent hallott.

Sudárabb a nagy isteneknél, soraikból fejjel kimagaslik:

 tagjai fönségesen nőttek, másokéinál ékesebben.

"Miféle sarj, kinek a magva ez? Miféle sarj, kinek a magva ez?

Az Ifjú Napnak, a Tavaszi Napnak, az Istenek Napjának sarja ő!

Egyiptomi teremtéstörténet

Az egyiptomi teremtéstörténetben is a víz és a fény játssza az alapvető szerepet és a mezopotámiai istenmítoszokhoz hasonlóan ez is egy gyönyörű költői vízió:

Kezdetben nem volt sem ég, sem föld, sem élők, sem holtak nem voltak, az alkotó és romboló elemek is dermedt tétlenségben nyugodtak Nun isten örvénylő mélyén. Nun volt az őselem, az ősvíz formájában létező istenlény. Az ő alkotórészeiből keletkezett a mindenség. Az ősvíz tükrét sűrű sötétség borította, mert a fény szent forrása is Nun keblében pihent. És az istenek létrehozója, a hatalmas Nun megteremtette a napvilágot. Az ősvíz színén zsenge csíra bukkant elő, és hamarosan kecses, sok színben pompázó lótuszvirággá nőtt. A virág áttetsző, zárt kelyhéből sejtelmes fény derengett, szirmai lassan kibomlottak, és egy tündöklő gyermek bújt ki belőle. Nun életre keltette Nefertumot, a napgyermeket. Nefertum felnyitotta szemét, a sötétség eloszlott, s a világot beragyogta az éltető fény.

A virágbölcsőjéből kiemelkedő napgyermek körültekintett, s a végtelen vízen egy cseppnyi hely sem akadt, ahol lábát megvethette volna. Ekkor a mélyből előhívta az őshalmot. Kilépett a szilárd talajra, és megteremtette Maátot, a mindenség törvényét, az igazság istennőjét, a holtak szívének túlvilági bíráját.

Indiai teremtéstörténet

Költői szépségében nem marad el ettől az indiai teremtéstörténet sem, amelyben a „gondolat” hozza mozgásba a mozdulatlan és sötét világot:

A Világéjszaka sötét, mindent elborító, mozdulatlan tengerének színén összecsavarodva nyugodott Ananta, a Végtelenség Kígyója, s rajta álomba merülve pihent Visnu, a mindenség létesítője és fenntartója, az egyetlen hatalom. Bensejében a világ egész tartalma mint nyugvó gondolat derengett, rajta kívül nem volt élet, nem mozdult semmi. Álmában egyszerre megrezdült benne a gondolat, és Visnu felébredt. Kinyitotta szemét, és látott. Abban a szempillantásban megindult a mozgás az odáig nyugvó ősanyagban. Visnu létesítő akarata kisarjadt, és köldökéből egy lótusz nőtt elő. A lótusz széttárta szirmait, és íme, a lótusz kelyhében ült Brahmá, az Egynek Teremtő Ereje.

Brahmá körül akart tekinteni, de nem moccant meg. Hogy mindenfelé láthasson, négy arca keletkezett. A gyökeret azonban, amelyből létre fakadt, nem látta, s ezért azt gondolta, hogy egyedül ő van, kívüle nincsen öntudat. Csak a lótuszt látta, mely őt hordozta, s ez a lótusz a világmindenség volt. Gondolkozni kezdett: "Honnan származott ez a lótusz? Honnan jöttem én magam?" Hosszú-hosszú időkig elmélkedett e kérdéseken, míg végül a szívében, lénye legmélyén felderengett egy kép: a mindenség sötét vizén s a Végtelenség Kígyóján nyugvó Egynek, a Világ Gyökerének a képe.

Tibeti teremtéstörténet

A tibeti teremtéstörténet filozófiai mélységével alkotott maradandót:

Kezdetben semmi sem létezett, sem tér, sem idő, sem valóság, sem jel, sem lét, sem nemlét. Ebből keletkezett minden, ami látható és tapintható.

Az első lény varázslatos átalakulási képességgel született. Megnevezte magát: "A Keletkező Világ Ura, Szent Győzedelmeskedő". És boldog volt, mert hatalma mindenre kiterjedt.

Ekkor a négy évszak még nem vált el egymástól, a nap, a hold, a bolygók és a csillagképek alig mozdultak, a mennydörgés, a villámlás, az eső, a jég, a fagy sem követték az évszakok változásait. A földnek nem volt ura, az erdők, a növények maguktól nőttek és szaporodtak. A kövek és a hegyek már létrejöttek, de még nem mozdultak, és a földrengés is ismeretlen volt. A föld aranyból volt. A folyók is megvoltak már, de még nem indultak el a tenger felé. Madarak és vadak is éltek az erdőkben, de még senki sem vadászott rájuk. Istenek is léteztek, de még nem hallgatták meg a könyörgéseket, és nem uralkodtak ég és föld felett. Létrejöttek a démonok is, de még nem kezdhették el romboló munkájukat. Voltak betegségek, de még nem okoztak kínt és fájdalmat. Volt már táplálék, de még senki nem fogyasztotta. A boldogság is létezett, de nem volt, aki felfogja. A nappal nem különbözött az éjszakától.

Japán teremtéstörténet

A japán teremtéstörténet fő jellegzetessége, hogy nem egy nagy kontinensen, hanem néhány szigeten fejlődött ki ez a kultúra. Megjelenik a mítoszban a káosz is, mint a későbbi világ előképe. Ez a gondolat az alapja a modern kozmológiának is.

Abban az időben, amikor a föld és az ég keletkezett, a magas égi mezőkön három istenség lakozott. Az istenek maguktól születtek, majd elrejtőztek. Később a föld óriás olajcseppként lebegett a víz színén, és úgy mozgott fel s alá, mint egy roppant medúza. Ekkor a bambusznád csírájából két újabb isten támadt, de ezek is elrejtőztek, és számos utódnak adtak életet. E dicső leszármazottak sarja volt az istenek atyja és anyja, Izanagi és Izanami. Az istenek őket bízták meg, hogy megszilárdítsák és megtermékenyítsék a kocsonyás, mozgó földet.

Izanagi és Izanami letekintettek a Menny Lebegő Hídjáról, és azt fürkészték, van-e föld valahol a híd alatt. Csillogó drágakőből hatalmas lándzsát készítettek, a fegyvert lehajították, és rábukkantak a tengerre. Ezután kiemelték a lándzsát a káoszból, a káosz cseppenként aláhullott, megszilárdult, és így keletkezett Onokoro-Jima, a Megdermedt Sziget. Ezután még egy szigetet alkottak a tengerben, és leszálltak a földre.

A japán mitológiában a Napnak és a Holdnak is kiemelt szerepe van, amit a következő sorok mutatnak:

Ekkor megszülték a nap istennőjét, Amateraszut, akit a "nagy istenség éji fényessége" néven ismernek, és már születése után oly gyönyörű volt, hogy szülei nyomban felküldték a mennyei létrán, hogy az égről sugározza le a földre ragyogó fényét.

Következő gyermekük, Tsuki-jumi, a hold ura lett. Tsuki-jumi tompa, ezüstös csillogása elhalványult nővére arany pompája mellett, de azért méltónak mutatkozott arra, hogy Amateraszu hitvese legyen. Ő is felkapaszkodott az égi létrán, de hamarosan civakodni kezdtek. Amateraszu megelégelve az örökös egyenetlenséget, így szólt:

- Távolodj el tőlem, nem akarlak többé szemtől szembe látni.

Ekkor az istenek elválasztották őket, a házastársak szétköltöztek, és a nappal elvált az éjszakától.

Kínai teremtéstörténet

A kínai teremtésmitológia a Jin és Jang egymást kiegészítő ellentétpárjára épül és itt is megjelenik a káosz mint a világ kialakulásának kezdete:

Kezdetben, amikor az ég és a föld még tojás alakú káosz volt, Pan Ku megszületett a tojásban, és itt élt tizennyolcezer esztendeig. És ekkor a Jang tiszta elemeiből megformálódott az ég, a Jin durvább elemeiből pedig a föld. Pan Ku a középpontban tartózkodott, és nap mint nap kilenc alkalommal alakult át: hol az ég, hol pedig a föld istene volt. Az ég naponta három méterrel emelkedett magasabbra, a föld három méterrel vastagodott. Így folytatódott ez tizennyolcezer éven át, míg az ég elérte a legnagyobb magasságot, és a föld a legnagyobb mélységet.

Pan Ku az élet kezdete. Ő az őse tizennyolcezer élőlénynek. Amikor Pan Ku meghalt, fejéből szent szirt lett, szeméből a nap és a hold, zsírjából a folyók és a tengerek, hajából és szőréből a fák és a növények. Pan Ku könnyeiből fakadt a Sárga Folyó és a Kék Folyam. Hangja alkotta a mennydörgést, lehelete a szelet, pillantása a villámot; az ég kiderült, amikor Pan Ku vidám volt, a rosszkedvétől elborult. Pan Ku volt a Jang és felesége a Jin, a teremtés férfi és női eleme.

Maya teremtéstörténet

Nézzünk át Közép-Amerikába is, hogyan képzeték el a mayák a teremtést. Itt is szerepet játszik a gondolat és a szó teremtő ereje, a fény és a vizek szétválasztása a föld létrehozásában:

Elmélkedtek (az istenek), és íme, megvilágosodtak, megjelent az Ősfényhajnal, és terveikben megjelent az ember.

Ennek utána elgondolták a teremtést, elgondolták a fák és folyondárok növekedését, az élet születését és az ember alkotását és a sötétségben és fénytelen éjszakában ekképpen szerezte mindezt Égszíve, az, akit Hurakánnak mondanak...

Miképpen legyen élet, és miképpen jöjjön létre világosság? Kinek kell gondoskodnia táplálékról és betévő falatról?

- Jöjjön immár, és legyen! Népesüljön be az üresség!

- Húzódjanak félre a vizek, és hagyják el helyüket! Tűnjenek elő a szárazok, és szilárduljanak! Legyen!

Így szóltak.

- Legyen élet és legyen világosság az égen és a földön! És ne legyen ragyogás, nagyság és dicsőség művükben és teremtésünkben, míg nem alkottunk embert, míg testet nem öltött az ember!

Így szóltak. És utána megcselekedték és így megteremtették a földet. Igen, így volt, így teremtették a földet. Nem volt föld, és így szóltak:

- Föld! - És egy szempillantás alatt létrejött a föld...

Ekképpen teremtetett a föld, így teremtetett általa, kinek neve Égszíve és Földszíve, és aki termékennyé tette a földet, mikor még várakozás borult az égre, és víz borult a szárazra.

Afrikai legenda

Fejezzük be teremtéstörténeti kalandozásunkat egy afrikai legendával:

Ezt az apám mesélte el nekem, ő meg az apjától hallotta; réges-régtől fogva, a világ kezdetétől száll így ez a történet.

A dolgok kezdetén, mindennek az elején, mikor még semmi se volt, se ember, se állat, se növény, se ég, se föld, semmi, semmi, de semmi, csak az Isten volt, és úgy hívták, hogy: Nzamé. És három Nzamé volt: Nzamé, Mebere és Nkva. Kezdetben teremtette Nzamé az eget és a földet. Az eget magának tartotta fenn. A földre pedig rálehelt, és lehelete nyomán megszületett a szárazföld és a víz, mindkettő a maga helyén.

Nzamé mindent megteremtett: az eget, a napot, a holdat, a csillagokat, az állatokat, a növényeket, mindent, mindent.

Természetesen minden teremtéstörténet eljut az ember megteremtéséig, de mivel szándékunk a modern kozmológiával való összevetés, ezért a természet létrehozására vonatkozó motívumokat emeltük ki. A következő részben térünk rá a modern, tudományra alapozott mitológiára, az ősrobbanás elméletérre: Az ősrobbanás és a teremtésmítoszok_II

A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés

„Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása, III. rész.

Bevezetés

Az első két részben mutattuk be, hogyan lehet értelmezni a fénysebességű forgás modellel az elektro-gyenge kölcsönhatást és béta bomlásban a paritássértést. Itt most továbblépünk és megvizsgáljuk a Standard Modell kiválasztási szabályát, amely megmondja, hogy milyen fermion állapotok között jöhet létre átmenet (az izospin megmaradási tétel) és választ keresünk arra a kérdésre, hogy a gyenge kölcsönhatás miért sérti nem csak a paritás szimmetriát, hanem a CP szimmetriát is, ahol a C művelet a töltés megfordítását, azaz a töltéskonjugációt jelenti. A könnyebb áttekinthetőség kedvéért először összefoglalom az előző két rész legfontosabb megállapításait, majd bemutatom, hogyan tud a fénysebességű forgás modell plauzibilis magyarázatot adni a Standard Modell egyes törvényeire.

A gyenge kölcsönhatási bozonok sajátmozgása

Az elektro-gyenge kölcsönhatást közvetítő bozonokat (fotont, W^- , W⁺, és Z) mint a tér fénysebességű forgásának és transzlációjának kombinációit írom le, ahol a haladási irány és a forgástengely lehet párhuzamos (foton) illetve merőleges egymásra (W és Z). Párhuzamos esetben nem lép fel a Coriolis csavaró erő, azaz nincs elektromos töltés (foton), viszont merőleges esetben van (W^- és W⁺), a Z bozon esetén a kétféle merőleges mozgás szuperpozíciója ad nulla töltést. Amikor a transzláció merőleges a forgástengelyre, akkor fénysebességgel növekszik a sugár, ami viszont ennek arányában csökkenti a forgási frekvenciát és evvel együtt a tömeget. Ezért a W és Z bozonok elveszítik a tömegüket és csak szűk tértartományban hozzák létre a kölcsönhatást és élettartamuk is rendkívül rövid. Ez a tömegvesztő képesség azonban lehetővé teszi, hogy különböző tömegű fermionokat átalakítsák egymásba.

A bétabomlás paritássértése 

A fénysebességű forgás centrifugális erejét a tér extrém torzulása által létrehozott erős gravitációja ellensúlyozza, ami egytengelyű forgások esetén S = 1 spinre vezet, szemben a kéttengelyű forgásokkal, amikor a spin S = ½. A forgások lehetnek jobb- és balmenetűek, amit az S_z spin komponens M = +1 és -1 sajátértékével jellemezhetünk. Időtükrözés esetén, amit a T szimbólummal jelölünk, a kétféle forgás átmegy egymásba. A hagyományos paritás, amit P-vel jelölünk, csak a részecskék külső terére vonatkozik és nem érinti a fermionok kettős forgásának királis szimmetriáját, ami a töltés előjelét határozza meg. Ebből következik, hogy bétabomláskor, amikor a neutron átalakul protonná egy elektron és egy (anti)neutrínó kibocsátása mellett, a hagyományos paritásszimmetria sérül, hiszen ez nem a teljes tükrözés, viszont kiegészítve a belső tér tükrözésével már megváltoztatja a kiralitást és a töltést, (ez a C töltéskonjugáció) azaz megfelel a CP műveletnek, és ez a szimmetria a bétabomláskor már nem sérül meg. A CP szimmetria kvantummechanikai magyarázatát Lev Landau adta meg 1957-ben.

A paritássértés kizárólag a gyenge kölcsönhatásnál valósul meg. A gravitációs és az erős kölcsönhatásban a részecskék sajátmozgása nem változik meg, ilyen változás csak az elektromágneses kölcsönhatásban lép fel a részecske-antirészecske annihiláció során. Az annihiláció azonban csak azonos tömegű, azaz azonos forgásfrekvenciájú részecskék között történik, amiért a két részecske sajátforgása szimmetrikusan változik meg, azaz a belső szimmetria nem sérül. Emiatt van, hogy az elektromágneses kölcsönhatás is rendelkezik a paritásszimmetriával hasonlóan mint a gravitáció és az erős kölcsönhatás.

A CP szimmetriasértés gyenge kölcsönhatásban

James Cronin és Val Fitch 1964-ben a kaonok bomlási mechanizmusát vizsgálva azt találták, hogy a töltéssemleges K⁰(ds) mezonok bomlása kismértékben különbözik a megfelelő antirészecskéhez (tehát K⁰(ds)-hez) képest. (Megjegyzés: az aláhúzás jelöli az antikvarkot). Ezért a felfedezésért 1980-ban a szerzők Nobel díjat kaptak.

A CP szimmetriasértés is jól magyarázható a fénysebességű forgásmodellel. A magyarázat lényege a W bozonok szimmetriatulajdonságában rejlik. A belső tér tükrözése nem változtatja meg a töltést, mert ez a W bozonoknál nem a királis szimmetriától származik, hanem azt a forgási és haladási tengely merőlegessége eredményezi. Viszont az időtükrözés megfordítja a Coriolis kölcsönhatás előjelét az M spin kvantumszámmal együtt, vagyis a W^- (M =1) bozon a W⁺(M = -1) bozonná transzformálódik.  A Q töltés és a spin tehát nem független és a kettő összege nulla: Q + M = 0. Ez a szabály azt is jelenti, hogy a negatív töltésű bozonnak nem lehet negatív az M értéke; és a pozitív töltéshez nem tartozhat pozitív M érték. A kaonbomlás szimmetriájánál tehát egyrészt szükség van a CP tükrözésre a fermionok miatt, másrészt a T időtükrözésre a W bozonok miatt, tehát a szimmetriát csak a CPT kombinált tükrözés biztosítja, ami megfelel a kísérleti megfigyeléseknek is.

A gyenge kölcsönhatás kiválasztási szabálya

A W bozonok Q + M = 0 szabályából követezik, hogy a fermionok egymásba alakulása csak az egyik spin állapotban lehetséges. A Standard Modellben ezt a gyenge izospin megmaradás elvével írják le. A kiválasztási szabály azonban egyszerűbben is megfogalmazható, mert a bozonok abszorpciója és emissziója úgy mehet végbe, ha az impulzusmomentum M kvantumszáma egységnyit változik, de ez össze van kötve a töltés azonos mértékű – de ellenkező előjelű – változásával, azaz ΔQ + ΔM = 0 lesz a kiválasztási szabály. Ez viszont kizárja, hogy a d kvark M = -½ állapotból menjen át u-ba, mert ekkor a ΔQ = 1 töltésváltozás M = -3/2 állapotba vinné át a kvarkot. Tehát a gyenge kölcsönhatás kizárólag az M = ½ spinű kvarkot tudja átalakítani, amikor is a képződő u kvark M = -½ spinű lesz. Ebből következik, hogy a W^- bozon elbomlásakor keletkező elektron és neutrínó spinje egyaránt M = ½ lesz.  Antikvarkoknál a helyzet megfordul: a d antikvarkot a W⁺ mezon viszi át az u antikvarkba, ha a spin M = -½. A Standard Modellben a kétféle spin állapotot szokás „left-handed” és „right-handed” (jobb- és balmenetűnek) nevezni és úgy jellemzik a gyenge kölcsönhatást, amely részecskék esetén csak a balmenetű, antirészecskék esetén csak a jobbmenetű fermionokra hat.

Mikor detektálható a CP szimmetriasértés?

Felvethető a kérdés, hogy a neutron bétabomlásában miért nem sérül a CP szimmetria, hiszen ezt is a W bozonok közvetítik. A CPT szimmetria azt jelenti, hogy a külső tér tükrözése mellett a töltést és a spint is tükrözzük. A C töltéskonjugáció nem változtatja meg a spint szemben a T időtükrözéssel. Mivel a neutronban két d kvark van és a neutron spin S = ½, így a d kvarkok egyaránt felvesznek M = ½ és -½ értéket, ugyanez vonatkozik a protonra is, ahol az u kvarkból szerepel kettő. Emiatt a kezdő és végállapot spin szimmetrikus, azaz rendelkezik az időtükrözési szimmetriával és így nincs szükség a T műveletre.  Evvel szemben a K⁰ mezonban két különböző tömegű kvark szerepel (d és s) és így a spin konfiguráció aszimmetrikus, azaz a T tükrözés lineárisan független állapotba transzformálja a kvark konfigurációt.  Végül is ez okozza, hogy a K⁰(ds) kaon más sebességgel bomlik, mint a K⁰(ds). 

A jelenség megfigyeléséhez az is szükséges, hogy a bomlás kizárólag a gyenge kölcsönhatáson keresztül történjen, mert az elektromágneses kölcsönhatás sokkal erősebb és így az annihiláció sebessége legalább nyolc nagyságrenddel meghaladja a gyenge kölcsönhatáson keresztül megvalósuló bomlást. Ez az egyik oka annak, hogy CP sértést csak néhány esetben lehetett megfigyelni. Másik ok, hogy töltéssel rendelkező mezonokban, erre példa a π⁺(ud) szerkezetű pion, a gyenge kölcsönhatás első lépése a W⁺ bozonná történő belső átalakulás, amikor egyidejűleg mind a két alkotó kvark eltűnik. A kvark annihilációs folyamatok azonban nem vezetnek paritássértéshez, ez akkor következik be, ha egyetlen kvark alakul át, ennek legismertebb esete, amikor a d-ből u kvark lesz. Barionok esetén még nem találtak CP sértő bomlást. Ennek további oka lehet a gyors bomlási sebesség, de nem zárható ki, hogy a jövőben sor kerül ilyen megfigyelésre is.

A kaon bomlásnál mért CP sértés azonban kismértékű, valószínűleg ennek nagyságát az határozza meg, hogy mekkora a tömegkülönbség a konfigurációban szereplő kvarkok között.  Emiatt nem véletlen, hogy jelentősebb CP szimmetriasértést sikerült 2001-ben a B⁰ (db) mezonnál megfigyelni, ahol a kvarkok közötti tömegkülönbség nagyobb, mint a K⁰ kaonban.  A legújabb eset, amikor 2011-ben  CP sértést figyeltek meg a D⁰(cu) mezon bomlása volt.

 Összefoglalás

Összefoglalva megállapítható, hogy a fénysebességű forgásmodell plauzibilis magyarázatot ad a CP szimmetriasértés okára a gyenge kölcsönhatásban és alternatív értelmezést ad a kölcsönhatás kiválasztási szabályára is.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

A földi erőforrások végessége

Napjaink ökológia problémái egyre nyilvánvalóbbá teszik, hogy itt a Földön egy véges világban élünk.  Az emberiség étvágyának exponenciális növekedése beleütközik a Föld véges eltartó képességébe és minél jobban megközelítjük ezt a határt, egyre gyakrabban figyelmeztet minket a természet hőhullámokkal, eltérülő tengeráramlatokkal, pusztuló élővilággal, a gleccserek olvadásával, viharokkal, árvizekkel, a sivatagok terjeszkedésével és még hosszan sorolhatnánk.  De ha túltekintünk az Univerzumhoz képest parányi földi világunkból beszélhetünk-e végességről?

Miért nem kell félnünk a földön kívüli civilizációktól?

Attól persze nem kell tartanunk, hogy megszállva távoli csillagrendszereket és galaxisokat komoly kárt tehetnénk az Univerzumban, mert ettől megvéd minket a fénysebesség végessége. Már a legközelebbi bolygókra eljutni is nagy kaland, a fényévekre lévő legközelebbi csillagokhoz még akkor se juthatnánk el, ha űrhajónkat a fénysebesség határára gyorsítanánk, mert ennek energiaszükséglete meghaladná a Föld teljes energiakészletét. Marad ezért a fantázia és a sci-fi világa. Az írók megpróbálnak kölcsönvenni a tudománytól bizonyos fogalmakat, hogy gondolatban eljussanak távoli galaktikákba, és hivatkoznak a gravitáció elméletében feltételezett féreglyukakra, vagy a kvantummechanikából a teleportálás lehetőségére, de ezek az elképzelések – még ha igaznak is bizonyulnának – technikailag kivihetetlenek. A féreglyuk például minden élőlény számára elviselhetetlen gyorsulást okozna, teleportálni pedig csak tömeggel nem rendelkező fotonok esetén van esély.

Szomorkodjunk emiatt, vagy örüljünk? Ennek igazából örülni kell, mert ez megvéd minket a földönkívüli civilizációk hódításától. Ha egyáltalán létezik még az Univerzumban rajtunk kívül értelmes civilizáció, akkor nálunk sokkal-sokkal fejlettebb kell, hogy legyen. Miért? Ez elég nyilvánvaló, ha belegondolunk mennyi időre volt szükség itt a Földön, hogy megjelenjen először az élővilág majd az ember! Ez több milliárd évbe került. Mekkora fejlődést ért el a technikai civilizáció az elmúlt ezer évben és azon belül is az utolsó száz évben?  Mekkora tehát az esélye, hogy egy másik civilizáció a miénkkel hasonló szinten legyen? Kevesebb, mint egy a tízmillióhoz. Ha tehát nem vagyunk egyetlenek itt a galaktikánkban, vagy egyáltalán az Univerzumban, akik értelmes lények, akkor nálunk elképesztő mértékben magasabb szinten állnak ezek a civilizációk! Még sincs még csak híradás sem róluk kozmikus üzeneteken át, nem hogy megjelentek volna a mi világunkban, ennek pedig örülnünk kell, mert elég, ha a földi civilizációnk történetére gondolunk. Mi történt például az amerikai indián kultúrával az európai hódítás után? Ez lehetne a mi sorsunk is.

Mekkorák vagyunk?

Az Univerzum parányai vagyunk. Ez vonatkozik nem csak ránk, hanem az egész Földre, az egész Naprendszerre, sőt még a Tejútrendszerre is.  Nézzük meg az arányokat:

                                                               méret       arány az előzőhöz         arány az emberhez      

Átlagos felnőtt testmagassága:         1m 60 cm                    1                                        1

A Föld átmérője                              12 758 km              8 millió                        8 millió = 8.10⁶

A Naprendszer sugara                        1 fényév             1 milliárd                            8.10¹⁵

A Tejútrendszer hossza            100 ezer fényév              százezer                            8.10²⁰

Az Univerzum nagysága         30 milliárd fényév          3 százezer                           2,4.10²⁶

Tehát parányiak vagyunk, de nem vagyunk kicsik, mert elindulhatunk a mikrovilág felé is. A molekulákban az atomok kötéstávolságánál 10 milliárdszor vagyunk nagyobbak, aminél az atommagok sugara tízezerszer és hozzánk képest pedig százbilliószor (10¹⁴) kisebb. Az arányokat kifejező számok mindkét irányban óriásiak, de mégis végesek.

A végtelen nagy és kicsi találkozása

A végtelenül nagy és a végtelenül kicsi egymásra épülő fogalmak, ha az egyik létezik, akkor ez a másikat is magával hozza. A matematika ezt úgy fejezi ki, hogy a határértékben nullához tartó mennyiséget a szintén határértékben végtelen számmal szorozva véges mennyiséghez juthatunk. Ebben az értelemben teremtheti meg a fénysebességű forgás a tér határértékben nulla tömegéből a részecskéket; és így tehet szert a nulla nyugalmi tömegű foton mozgási tömegre az E = h.ν = m.c² ekvivalencia elv szerint a fénysebességű terjedés miatt.  A speciális relativitáselmélet szerint a hozzánk képest nagy sebességű objektumok tömege megnövekszik és a tömegnövekedés mértéke végtelen lesz, ha eléri a fénysebességet. Ez vonatkozik a neutrínókra is, melyek haladási sebessége minden eddigi mérés szerint éppen c! Persze minden mérésnek véges a pontossága és ez hagy egy kis kibúvót, mert a hiba határon belül feltehetjük, hogy a haladási sebesség ennek mértékében elmarad c-től és ebből becsülhetünk egy parányi tömeget, ami azonban kisebb lenne, mint az elektron tömeg milliomod része.  De meggyőződésem, ahogy majd növekszik a mérés pontossága úgy fog továbbcsökkenni ez a tömeg. Amikor a Nobel Bizottság bejelentette, hogy Kadzsita Takaaki és Arthur B. McDonaldnak ítélték oda a 2015 évi díjat, elhangzott az indoklás, mely szerint a kitüntetett tudósok a neutrínó oszcilláció felfedezésével bizonyították, hogy a neutrínónak van tömege. Ennek oka, hogy nulla tömeg esetében – ami egyébként a Standard Modell egyik állítása – nem lehetne három különböző neutrínóról beszélni. A korábbi bejegyzésekben, például a „Nyomozás a sötét anyag után” és a „Dirac egyenlettől az általános fermion egyenletig” kifejtettem, hogy a tömeg és a töltés kétdimenziós mennyiség és a relativisztikus tömegnövekedés törvénye csak az egyik (a diagonális) komponensre vonatkozik, ezért nincs akadálya, hogy a másik komponens a fénysebességű haladás mellett is különbözzék nullától. Ennek értelmében a neutrínó oszcilláció jelensége nem azt bizonyítja, hogy van tömege a részecskének, hanem azt támasztja alá, hogy a tömeg valójában kétdimenziós mennyiség.

Az idő és tér határai: a Planck idő és hossz

Jelenlegi felfogásunk szerint az Univerzum térben és időben véges. Ez a végesség azonban nem csak a méretére és korára vonatkozik, hanem a tér mikro-szerkezetére is. Kell lenni egy végső határnak, mikor a tér és idő már nem darabolható kisebb részletekre. Az ősrobbanás elmélete szerint az Univerzum kezdetei a Planck időig, amely 10^-43 s, vezethetők vissza, ez pedig azaz idő, ami ahhoz kell, hogy a fény vákuumban megtegye a Planck hossznyi utat. A Planck hossz viszont a térfelbontás elvi határa, értéke

Ez a hosszúság dimenziójú mennyiség a ℏ Planck állandótól a G gravitációs állandótól és a c fénysebességtől függ. Ez a hossz még a proton sugaránál is 20 nagyságrenddel kisebb, ezért nincs rá kísérleti lehetőség, hogy megvizsgáljuk ennek fizikai szerepét. Ez az elméleti érték azon az elven alapul, hogy a gravitáció is kvantumos természetű és a bizonytalansági elv szerint, ha a távolság ennél kisebb, akkor valamennyi fizikai mennyiség mérhetetlenné válik. Elméleti szempontból is kétségeink támadhatnak a Planck hosszal kapcsolatban, mert eddig minden olyan próbálkozás, amely megkísérelt a gravitációra felállítani egy konzekvens kvantumelméletet sikertelen maradt.

 Könnyen eljuthatunk azonban a Planck hossz fogalmához a fénysebességű forgások modelljével. A klasszikus Newton egyenlet szerint az ω frekvenciájú körmozgás centripetális erejét a tömegvonzás egyenlíti ki:

Innen kapjuk a második Kepler törvényt:

Tételezzük fel, hogy a Newton által felismert gravitáció létrehozhat fénysebességű forgást, azaz ω.r = c, helyettesítsük ezt a fenti Kepler törvénybe, ekkor a forgási sugár r = G.M/c² lesz. A korábbi bejegyzésekben ismertetett elképzelésünk szerint a fénysebességű forgás hozza létre ezt az M tömeget, amikor is a nyugalmi (valójában kinetikus) energiát az extrém mértékben torzult tér potenciális energiája egyenlíti ki:

Itt c²-el osztva kapjuk a tömeget: M = ℏ/r.c, amit az r = G.M/c² kifejezésbe helyettesítve és átrendezve jutunk el a következő alakhoz:

Tehát a Planck hossz nem más, mint az a sugár, amelynél a szokásos gravitációs erő képes létrehozni a fénysebességű forgást; és ennél a sugárnál a szokásos gravitáció ereje azonos lesz az erős gravitációval. Korábbi bejegyzésekben (például A részecskefizika nyitott kérdései) már kifejtettük, hogy a kvantum eredete az erős gravitáció, így a Planck sugárnál valóban átlépünk a kvantumgravitáció birodalmába.

A fotonok széles energiatartománya

Az Univerzum legnagyobb és legkisebb objektumait egyaránt a fotonok segítségével vizsgálhatjuk. De van-e olyan energia és frekvencia tartomány, amit már nem léphet át a foton? A fény „atomja” a foton elektromágneses hullám, ami azonban csak egy rendkívül szűk frekvenciatartományban látható szemünkkel. Jellemezhetjük a fotonokat akár frekvenciával, akár hullámhosszal, mert a c fénysebesség a kettő szorzata: c = ν. λ. Az egyes fotonokhoz a frekvenciával arányos energia is tartozik: E = h.ν, ahol h a Planck állandó, amely egyben a foton impulzusmomentumát is meghatározza: ℏ=h/2π. Fussunk végig azon a frekvenciaskálán, amit átfognak a fotonok!  Alulról kezdve az ismertetést hivatkozhatunk hálózatunk váltóárama is, amelyik kis energiájú 50 Herzes fotonokat bocsát ki. Haladjunk tovább az audio, majd a rádiófrekvenciákon, az utóbbinál a kilométeres hosszúhullámoktól kezdve egészen a méteres URH tartományig, ahol a frekvencia 100 kHz és 100 MHz között változik. Ezt követi a centiméteres mikrohullámú tartomány nagyjából 3 és 100 GHz között (1 GHz = 1000 MHz). A milliméteres és mikrométeres tartományt 100 GHz és 430 THz között (1 THz = 1000 GHz = 10¹² Hz) infravörös sugárzásnak hívjuk, amelynek hatását melegítő hatás keresztül a mindennapi életben is észleljük. Ezt követi a látható fény a vöröstől  (0,7 μm, 430 THz) az ibolyáig  (0,4 μm, 750 THz, 1 mm = 1000 μm). Az efölötti UV frekvenciás sugárzást csak a bőrünk érzi meg, amikor leégünk, vagy lebarnulunk, ez a 400 nm (4,4.10¹⁴ Hz) és 10 nm (3.10¹⁵ Hz) közötti tartomány (1 μm = 1000 nm). Ennél is rövidebb hullámhosszú a röntgen vagy X sugár, ami már a molekulákban és a kristályrácsokban az atomok közötti távolság nagyságrendje, (a hullámhossz 10 nm és néhányszor 10 pm között van, ahol 1000 pm = 1 nm). A hozzá tartozó frekvencia tartomány 3.10¹⁶ és 3.10¹⁹ Hz helyezkedik el, a röntgensugárzás energiája pedig nagyjából 0,1 keV és 1 MeV közé esik (1 eV = 1,6.10^-19 J). A sugárzás jelentős ionizáló hatása miatt már élettanilag veszélyes. Ezt érdemes összevetni az elektron nyugalmi energiájával, amelyik közelítőleg 0,5 MeV. Az elektron tömegéhez is rendelhetünk frekvenciát a részecskék kettős természete miatt, részben hullámként, részben korpuszkulaként viselkednek, amit kifejezhetünk a hullámok és a nyugalmi tömeg energiájának azonosságával: h.ν = m.c², azaz ν = m.c²/h. Az elektron így számított deBroglie  frekvenciáját tekintik a röntgen sugárzás felső határának.

Az elektromágneses sugárzás következő tartományát nevezzük gammasugárzásnak, amit először a radioaktív bomlások során figyeltek meg, ennek alsó határát jellemezhetjük az 1 MeV energiával, illetve a 10¹⁹ frekvenciával és a 10 pm alatti hullámhosszal. Ez a 10 pm hossz már az atommagokat alkotó nukleonok sugarának nagyságrendje. Szintén gamma sugárzás jön létre az elektron és a pozitron annihiláció során, mert ekkor a felszabaduló energia 1 MeV. Az utóbbi folyamat megfordítása a párképződési folyamat, ami az 1 MeV energia feletti gamma besugárzás hatására jöhet létre. A proton és antiproton találkozásakor szintén szétsugároznak a részecskék, az ekkor keletkező gammasugarak energiája további három nagyságrenddel nagyobb, ekkor az energia az 1 GeV tartományba esik, a frekvencia pedig 10²² Hz fölé nő.  Szintén gammasugarak jönnek létre a kozmikus sugárzás hatására is, amit elsősorban nagy energiájú elektronok hoznak létre. A Napban és csillagokban a nukleáris láncreakciók során kibocsátott gammasugarak energiája nem haladja meg a 10 MeV értéket, viszont csillag óriások, a kvazárok, a természet „részecske gyorsítói”, és az egymásnak ütköző neutron csillagok ennél jóval nagyobb energiájú kozmikus részecskéket, és ezek révén gammasugarakat képesek kibocsátani. Az innen származó sugárzás rövid gamma kitörésekben jelentkezik. A sugárzás energiája eléri az 1-10 TeV (1 TeV = 1000 GeV) nagyságrendet is, ez pedig már azt jelenti, hogy a sugárzás frekvenciája a 10²⁵- 10²⁶ Hz körül lehet, a hullámhossz pedig hat-hét nagyságrenddel lesz kisebb, mint egy atommag, azaz 10^-16-10^-17 m tartományba esik. Összehasonlításként érdemes megemlíteni, hogy ugyanebbe a nagyságrendbe esik az LHC gyorsító által elért legnagyobb ütközési energia is (jelenlegi maximum 13 TeV), amikor egymással szembefutó két proton nyalábot ütköztettek egymással.

De van-e még feljebb a 10 TeV tartomány fölött és van-e egyáltalán felső határ? Az nagyon valószínű, hogy nem 10 TeV körül van a kozmikus sugárzás felső határa, mert a kvazárok óriási tömege a gravitáció révén képes lehet ennél nagyobb energiájú sugárzást is kibocsátani, sőt akár itt a Földön is építhetünk az LHC-nél akár tízszer nagyobb energiájú gyorsítót, habár ennek technikai nehézségei és költségei beláthatatlanul nagyok lennének.

A kérdést úgy is felvethetjük, hogy van-e elvi határa az elektromágneses sugárzás frekvenciájának, ugyanis minél nagyobb a frekvencia annál rövidebb lesz a hullámhossz, annál rövidebb lesz azaz idő, ami alatt egy hullám kialakul. A legrövidebb élettartam, ami szükséges egy részecske detektálásához 10^-24 s, aminél a 10 TeV energiájú sugárzás periódus ideje már két nagyságrenddel rövidebb, ugyanakkor az ősrobbanás kozmológiai elméletében feltételezett legrövidebb idő, a Planck idő 10^-43 s, ettől még óriási távolságra van. Tehát alighanem még távol az a határ ameddig a foton energiája tovább növekedhet, amikor a foton hullámaival szétszabdalt idő és a tér már nem bontható tovább még apróbb elemekre.

Az emberléptékű és a természetes fizikai egységek

Amikor arról beszélünk, hogy mi a „kicsi” és mi a „nagy”, ekkor mindig valamilyen egységhez viszonyítunk. Minden fizikai mennyiséget három alapegységhez kapcsolunk, ez a tömeg, a hosszúság és az idő. Szokásos egységeket emberléptékűre választjuk, a kilogramm igazodik mindennapi kenyerünkhöz, a méterben megjelenik lépteink hossza, a másodpercben szívünk lüktetése. Az Univerzumot is magunkhoz mérjük, de megtehetjük fordítva is, amikor a természeti törvényekhez igazodó egységeket választunk. Lehet egység a fény sebessége, a c, a kvantumok alapja a h Planck állandó, de szükség van még egy harmadikra is. Erre az elektron m tömege lenne a legalkalmasabb, mert az elektron stabilis és tovább nem osztható, szemben például az összetett protonnal, melynek tömege az atomsúlyok egységét képezi (kis korrekcióval a kémiában).  Az elektron tömege azért is alkalmas erre, mert ettől függ az atomok és molekulák mérete, az atomok közötti kémiai kötés ereje, a látható szín frekvenciája, sőt még a víz fagyáspontja is. Tehát az elektron tömege döntő mértékben határozza meg, hogy milyen az a világ, amiben élünk és magunk is milyenek vagyunk. Ebben az egységrendszerben a hosszúságot az elektron Compton hullámhossza λ = h/m.c adja meg, az időt pedig definiálja, hogy ezt a távolságot milyen gyorsan futja be a fény: t = r/c = h/mc². Ez lehetővé teszi a fizikai képletek leegyszerűsítését, de rendkívül kényelmetlen mindennapjainkban az óriási számértékek miatt.

Záró gondolat

Az Univerzumban való kalandozásunk során legjobb útitársunk és kitűnő kalauzunk a foton. Segít bepillantani a legparányibb objektumok belsejébe, hírt adhat a legrövidebb életű részecskékről, színes beszámolót nyújt földi világunkról, eljuttatja hozzánk az ősi Univerzum üzenetét és megmutatja nekünk a legtávolabbi galaxisokat is.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Barangolás a kvarkok és elemi részecskék világában

Evvel az írással kettős célom van. Egyrészt a Standard Modell alapján bemutatom, hogyan lehet felépíteni az összetett részecskéket a kvarkkoncepció alapján, másrészt túllépve a jelenlegi elmélet keretein kísérletet teszek a részecskék karakterisztikus paraméterének, a tömegüknek új módon való meghatározására.

A részecskék osztályozási szempontjai

Az atomot alkotó protonokon, neutronokon és elektronokon kívül a kozmikus sugárzásban és a nagy energiájú ütközéses kísérletekben számos egyéb részecske figyelhető meg. Az elsőleges osztályozási szempont a részecskék spinje, ami ha egészszám, akkor bozonokról, ha félegész – konkrétan  ½ és 3/2  – akkor fermionokról beszélünk. A másik fontos osztályozási szempont a részecske töltése, ami valamennyi esetben az elektron, illetve a proton töltésének egészszámú többszöröse, vagy nulla. Az újabb és újabb részecskék megfigyelése, ami már száz fölött jár, felvetette az igényt további osztályozási elvek kidolgozására. Ennek során Murray Gell-Mann 1964-ben felvetett egy rendkívül szokatlan hipotézist, amikor feltételezte a kísérletileg megfigyelhetetlen törttöltésű részecskék létezését, amit később kvarkoknak nevezett el az irodalom. Ennek értelmében az elemi részecskék többsége nem is „elemi” hanem felbontható két, illetve három kvarkra. Az új osztályozás a fermionok közül csak az elektront, a müont, a tau részecskét és neutrínókat tartja valódi elemi részecskéknek, továbbá a kölcsönhatást közvetítő bozonokat, nevezetesen az elektromágnesesség esetén a fotont, a gyenge és erős nukleáris kölcsönhatásokban a W, Z bozonokat illetve a gluonokat. A modell szerint az összetett bozonokat egy kvark és egy antikvark, míg a fermionokat vagy három kvark, vagy három antikvark alkotja. Az előbbi részecsketípust nevezik mezonoknak, az utóbbit barionoknak, de szokás a két típust együtt hadronoknak nevezni.  A valódi elemi részecskék közé sorolják a müon mezont is, mert tulajdonságai – a tömeg kivételével az elektronéval egyeznek meg –  ezért a jelenlegi nevezéktan szerint ezt már az elektronnal és a hasonló tulajdonságú tau részecskével, valamint a neutrínók három típusával együtt leptonoknak nevezik.

Mi tette szükségessé a kvarkelméletet?

A kvarkok tulajdonságaival már két írásban is foglalkoztunk („A Dirac egyenlettől az általános fermion egyenletig” és ” Nyomozás a sötét anyag után”).  Itt most tekintsük át, hogyan juthatunk el a törttöltésű részecskék feltételezéséhez.  Ehhez támaszkodnunk kell a spinek és a töltések összegzési szabályaira. Kiindulópontunk szerint a kvarkok s =  ½ spinű fermionok, mert ezt követeli meg az izotróp szimmetria (Lásd: „The origin of covariance in the special relativity”). Ebből már adódik, hogy az S = 0 vagy 1 spinű mezonokhoz páros számú, az S = ½ vagy 3/2 spinű barionokhoz páratlan számú összetevő kvarkra van szükség. Az eddig megfigyelt mezonok és barionok esetén elegendő két illetve három kvarkot feltételezni. (Friss hír: a nagy energiájú LHC kísérletekben találtak öt kvark együttesére utaló részecskét, ami úgy értelmezhető mint egy összeépült mezon és barion, de ez a következő gondolatmenetet  nem érinti).  A mezonok töltése lehet nulla, +e és –e, a barionok töltése ezen kívül még felveheti a +2e és –2e értéket is. A lényeg, hogy 2e töltésű mezont, illetve 3e töltésű bariont nem lehetett megfigyelni. A q = ±½e töltés ugyan felépíthetné a mezonokat, de nem magyarázná meg a barionok töltését. Három kvark együttese viszont csak úgy adhat egészszámú töltést, ha az egyedi kvarktöltés az e/3 harmadolt elemi töltés többszöröse, pontosabban szólva q = ±⅓e és ±⅔e lehet, mert az ennél nagyobb töltés esetén az eredő részecsketöltés meghaladná a megfigyelt maximális értékeket. Ekkor viszont a két kvarkból felépülő mezonoknál az egész töltés létrejötte megkívánja, hogy egy kvark és egy antikvarkból épüljön fel (a kvark és antikvark csak a töltés előjelében különbözik), míg a három komponensű barionok  vagy három kvarkból, vagy három antikvarkból állnak össze.  A kvarkoknak két alaptípusa van (erre szokás a flavor szót használni): az up és a down, amit röviden u és d szimbólummal jelölünk. Az előbbi töltése ⅔e pozitív elemi töltés, az utóbbié –⅓e. Minden kvarknak van antirészecske párja, az anti-up, azaz u és anti-down, azaz d, amelyek töltése      –⅔e és ⅓e. A kvarktöltések előjele  a proton +e töltéséből származik, amit az elmélet két u és egy d kvarkkal értelmez, amikor is:  2*⅔e – ⅓e = e. A neutron zérus töltése egy u és két d töltéséből adódik össze, hiszen ekkor ⅔e – 2*⅓e = 0. Az antirészecskék töltésének előjele épp fordított, ami tehát az összetevő kvarkokra is érvényes. A részecskék nagy száma annak a következménye, hogy a kvarkoknak három generációja létezik, amelyek egymással tetszőleges módon kombinálódhatnak.

Mekkora a kvarkok tömege: a renormálási eljárás

A kvarkokkal csak egy baj van: nem lehet őket megfigyelni, azaz nincs szabad kvark, kizárólag mint a hadronok alkotórészei léteznek, legalább is a tudomány mai állása szerint.  Ebből adódik, hogy nyugalmi tömegükre is csak becsléseket lehet adni az úgynevezett renormálási eljárás keretében. A Standard Modell három generációra osztja fel az elemi részecskék családját, ez vonatkozik a kvarkokra is. A család magasabb generációit a nagyobb nyugalmi tömeg különbözteti meg az u és d kvarkoktól, a +2/3e töltésű u típusba tartozik a második generációs charm (c) és a harmadik generációs top (t), míg a -1/3e töltésű d típusba a strange (s) illetve a bottom (b). Közvetlenül nem lehet megfigyelni egyik kvarkot sem (a top kvark ráadásul nem is létezik kötött állapotban rövid élettartama miatt, csak nagy energiájú bomlási reakciókból lehet létezésére következtetni), ezért a kvarkok tömegét különböző mezonok és barionok tömegének összehasonlításával lehet meghatározni. A módszer bizonytalansága, hogy nincs garancia arra, hogy két hadron tömegkülönbsége azonos az alkotó kvarkok tömegkülönbségével, mert a tömeghez járulékot ad az erős, a gyenge és az elektromágneses kölcsönhatás potenciális energiája és ezen kívül a komponensek kinetikus energiája is, ami különbözhet az egyes részecskékben.

A renormálási eljárás újragondolása a relativitáselmélet alapján

A részecskék fénysebességű forgására alapított modellünkben a töltést a részecske kettős forgásának kiralitásához rendeljük, de hogyan fér össze ez a kép a törttöltések létezésével? Itt a kvantummechanikai szuperpozíció elvére lehet támaszkodni: a kvarkok két különböző kiralitású héj szuperpozíciójából épülnek fel (Lásd „A Dirac egyenlettől az általános fermion egyenletig”). Ebből a felfogásból következik a tömeg újraértelmezése is. A relativisztikus kovariancia elv szerint fénysebességű mozgások esetén az energia nem lineárisan tevődik össze a kinetikus és nyugalmi energiából , hanem négyzetesen, ahogy egy derékszögű háromszögben az átló hosszát számoljuk ki a két befogó négyzetéből (Pitagorász tétel). Ezt a négyzetes összegzési szabályt fogjuk alkalmazni összetett részecskékben, amikor az egyes kvarkok tömegét összeadjuk. Áttekintve a mezonok és barionok táblázatát 16 olyan párt lehet találni, amelyek csak egy vagy két d és u típusú kvarkban különböznek. Korábbi bejegyzésünkben („Nyomozás a sötét anyag után) kimutattuk, hogy az ilyen párokban a tömegkülönbség fordítva arányos a részecskék tömegével, ami mutatja a négyzetes összegzési szabály helyességét.

A kvarkok kicserélődési kölcsönhatása

Egy másik törvényszerűség, amit számításba veszünk, hogyan változik meg az azonos kvark összetételű részecske tömege a spin multiplicitás függvényében. Az s = ½  spinek összegzési szabálya szerint a két kvarkot tartalmazó mezonok spinje S = 0 (pszeudoskaláris mezon) vagy S = 1 (vektor mezon) lehet. Két azonos pályán tartózkodó elektron kölcsönhatása esetén az S = 1 triplett és az S = 0 szingulett spin állapotok szeparációját a Heisenberg-féle kicserélődési energia adja meg: H_exch = J.S₁.S₂. Ekkor az S eredő spinhez tartozó energia: E__S = J(S(S+1) – 3/2)/2, ami azt jelenti, hogy a triplett-szingulett szeparáció J-vel egyenlő. A hadronokban kötött kvarkok esetén az extrém relativisztikus körülmények miatt az energia tagok négyzetes összegzési szabálya érvényes, ezért a triplett-szingulett szeparációból számolható kicserélődési energiára

 összefüggést várhatunk. Ennek ellenőrzésére összehasonlítjuk a triplett-szingulett szeparációból számolható J értékeket a lineáris és a négyzetes szabály esetén. Összesen hét olyan lényegesen különböző esetet találtunk a mezonok esetén, ahol az összevetés elvégezhető.  A táblázatból jól látható, hogy a négyzetes szabállyal számolva  J értéke nem függ a mezonok tömegétől és átlagértékben J = 770 MeV lesz.

1. Táblázat: A triplett-szingulett szeparáció függése a mezonok tömegétől a lineáris és négyzetes addíció esetén

A kvarkok energiafüggése a spin multiplicitástól fordított Hund szabálynak engedelmeskedik. Elektron konfigurációkban az azonos spin állapotú részecskék között, amikor a spin maximális értéket vesz fel a kicserélődési kölcsönhatás csökkenti a taszító erőt, ezzel szemben a kvarkok között az erős kölcsönhatás vonzást hoz létre, aminek erősségét csökkenti a nagy spinű állapotban a kvarkok közötti kicserélődési energia. Ennek tulajdoníthatjuk, hogy mezonok esetén, és mint látni fogjuk barionoknál is, mindig a nagy spinű állapot rendelkezik nagyobb energiával.

Kvarkok kicserélődési energiája barionokban

Barionokban a három s = ½ spin eredője S = ½ és S = 3/2 lehet az impulzusmomentum összegzési szabálya szerint, az előbbit nevezzük dublett, az utóbbit kvartett barionoknak. A kvartett barionok azonosítása során kiderült, hogy van olyan részecske is, amelyik három azonos kvarkból épül fel, erre példa a Δ⁺⁺ (uuu) részecske. Ennek a részecskének a létezése fontos szerepet játszott a kvarkelmélet kidolgozásában. Mivel a kvark s = 1/2 spinű fermion, így csak két lehetséges spin állapota van, következésképp a Pauli-elv nem engedi meg a feltételezett uuu konfigurációt, hiszen ekkor legalább két fermion azonos állapotba kerülne. Ezért a Pauli-elv kvarkokra való kiterjesztése miatt szükség volt egy új kvantumszámra, amit szín-kvantumszámnak neveztek el és ez a +1, 0 és -1 értékeket veszi fel. Ez a kvantumszám azonban kizárólag a kvarkoknál jelentkezik, míg a belőlük képzett hadronoknál nem. Ez úgy értelmezhető, hogy a kvarkok három különböző állapotban lehetnek, és a szín-kvantumszámok összege nulla lesz, amikor a hadronok képződnek, hiszen ekkor  1 + 0 -1 = 0. Ezt hozták párhuzamba a színekkel, ahol a három alapszín összeolvadása  „fehér” lesz.  Innen származik a kvantumszám elnevezése. Mezonoknál ez annak felel meg, hogy az antikvark mindig a hozzá kapcsolt kvark komplementer színével rendelkezik, míg barionokban a három kvark színe egymástól különbözni fog. A kvark konfigurációk szempontjából ennek az a következménye, hogy ha három azonos kvarkból épül fel a barion, akkor kizárólag S = 3/2 kvartett spin állapot jöhet létre, ha a három kvarkból kettő azonos, akkor a kvartetten kívül lesz egy S = ½ dublett is, míg ha a három kvark eltérő, akkor a kvartett mellett két különböző S = ½ dublett is lesz.

Hasonlítsuk össze a lineáris és négyzetes összegzési szabály hatását a dublett-dublett szeparáció esetén, ami akkor jön létre, ha három különböző típusú kvarkból épül fel a barion.

2. Táblázat: A dublett barionok energia különbsége a lineáris és négyzetes összegzési szabályok esetén

Csupán négy olyan kvark konfiguráció van, ahol az összehasonlítás elvégezhető. Mindkét számításban növekszik a szeparáció a részecskék tömegével, de a négyzetes szabály esetén ez jelentősebb, ekkor a tömeggel arányosan változik a szeparáció, amit a 2. táblázat utolsó oszlopa mutat. A kvark kicserélődési energia  H_exch = J(S₁.S₂+S₁.S₃+S₂.S₃), ha megegyezik a spin-spin csatolás a barion három kvark-kvark párjában, ebben az esetben a két eredő spin dublett energiája egyenlő lesz. A megfigyelt jelentős dublett-dublett szeparáció ezért arra mutat, hogy aszimmetrikussá válik a három kvark kölcsönhatása – például az egyik pár csatolása jóval erősebb a másik két párhoz képest – és következésképp szétválik a két dublett energiája. A tömeg függvényében növekvő szeparációt úgy értelmezhetjük, hogy az aszimmetria növekszik, amikor a „domináns” kvark (az elsőben s, a második és harmadikban c, a negyedikben b) tömege egyre jobban meghaladja a másik két kvarkét.

Hasonlítsuk össze a kvartett állapot energiáját a dublettel, (ha kettő van,akkor a felsővel), amit a következő táblázat mutat.  Az első példa mutatja a delta részecskék viszonyát a két nukleonnal, tehát a protonnal és a neutronnal. Ezek a barionok a két „alap” kvarkból, tehát u és d kombinációkból épülnek fel. A neutron és proton tömegének a kis különbsége, valamint a négy lehetséges delta részecske (uuu, uud, udd és ddd) tömegének egyezése a kísérleti hiba határán belül, arra mutat, hogy az u és d kvarkok tömege kismértékben különbözik, és az uu, ud iletve dd típusú kvarkok közötti csatolás megegyezik. A korábbi bejegyzésben (Nyomozás a sötét anyag után) azt a kérdést vizsgáltuk, hogy mekkora azoknak a kvark konfigurációknak a tömegkülönbsége, amelyek csak abban különböznek, hogy egy u kvark helyett egy d kvark szerepel.  Ekkor is azt találtuk, hogy a négyzetes összeadási szabály értelmezi helyesen a szeparáció tömegtől való függését. Az összevetés alapján meghatároztuk a két kvark tömegének különbségét , de a kettő összegére nem kaptunk felvilágosítást. Ezt majd a mezonok segítségével fogjuk meghatározni. Előbb azonban vizsgáljuk meg a kvartett- dublett szeparáció változását a lineáris és a négyzetes összegzési szabály esetén.

3. Táblázat: Barion kvartettek és dublettek energiája és szeparációja a lineáris és négyzetes összegzési szabályok alapján

A táblázatból látható, hogy az energiaszeparáció a lineáris modellben nagymértékben csökken a nehezebb barionoknál, míg a négyzetes szabály nem vezet ilyen trendhez. Barionokban az értékek szórása nagyobb, mint amit a mezonok esetén láttunk, de az átlagérték 703 MeV, meglehetősen közel van a mezonoknál tapasztalt 770 MeV értékhez.  Ez a megfigyelés is alátámasztja, hogy a négyzetes összegzési szabály jól adja vissza a tömegek változási szabályát.

A mezonok tömege

A fentiekben vázolt tendenciák segítségével eljárást javasolunk a hadronok tömegének származtatására a kvarkok renormálási tömegei, a közöttük fellépő kicserélődési energia, valamint a kölcsönhatási mező járulékai alapján. Ennek érdekében feltételezünk egy valamennyi hadron esetén alkalmazható összefüggést. Ennek célja, hogy előre lehessen jelezni mekkora a várható tömege a standard modellből következő, de eddig nem detektált részecskéknek. Először a mezonokat vizsgáljuk meg, ami alapján megadhatjuk az öt kvark renormálási tömegét és a kölcsönhatási mező energiajárulékát.

A mezonok családjának legstabilabb és legkisebb tömegű tagja az u kvark és d antikvarkból felépülő pion részecske (π⁺: 140 MeV, π⁰: 135 MeV), amelynek töltéssel rendelkező tagja különösen hosszú életű (10**^-8 s). A nagy stabilitás oka, hogy ez a részecske kizárólag a gyenge kölcsönhatáson keresztül bomlik, szemben az olyan mechanizmusokkal, amiben a gammasugárzás játszik domináns szerepet. A pionok fontos szerepet játszottak az erős kölcsönhatás értelmezésében, hiszen Yukawa javaslata szerint ezek közvetítik a nukleonok közötti erős kölcsönhatást. Ezt arra alapozta, hogy a kölcsönhatás rövid hatótávolsága jó összhangban van a pionok tömegével. A kvarkelmélet kidolgozása azonban más alapokra helyezte az erős kölcsönhatást, amit a szín-kvantumszám kombinációkkal definiált gluonok közvetítenek a kvarkok között, a nukleonok közötti vonzóerőt pedig a gluonok által létrehozott kölcsönhatás polarizációs effektusaként értelmezik. A pionok tömege közel van az u és a d kvarkok négyzetes szabály alapján számított tömegeinek különbségéhez, ezért kiindulópontunk az a feltevés, hogy a pionok tömegét alapvetően a két összetevő kvark renormálási tömege határozza meg. Más szóval ebben a részecskében a különböző energiajárulékok kompenzálják egymást. Ez alapján kapjuk, hogy az u kvark tömege 61 MeV, míg a d kvarké 122 MeV.

Az 5 kvarkból és 5 antikvarkból összesen 2x5x5 = 50 mezon építhető fel, ha az S = 0 és S = 1 mezonokat egyaránt számításba vesszük. A top kvark nem szerepel a számításokban, mert gyors bomlása miatt nem alkot megfigyelhető mezont és bariont.  Összesen 29 mezonra található eltérő nagyságú tömegadat, melyekben a pionok és a szintén u és d kvarkból felépülő triplett mezonok (ρ⁺ és ρ⁰) mellett vannak s, c és b kvarkokat is tartalmazó részecskék: η, K, D, B,ω, φ, ψ, y, ahol a töltésre, spinre és a domináns kvarkra utaló indexek adnak útbaigazítást az összetételről. A töltéssel rendelkező mezonoknak van antirészecske párja is, amelyeknek a tömege azonos a megfelelő részecskével. Egyetlen olyan triplett mezon van (cb összetételű), amelynek nem határozták meg a tömegét, tehát csaknem az összes mezont már sikerült detektálni.

A 29 mezon tömegét a következő összefüggés alapján számítjuk::

Itt m₁ és m₂ a két kvark renormálási tömege, X₁ és X₂ a két kvark mezőjáruléka, n = 0 a pseudoskaláris és n = 1 a triplett mezonok esetében, J_m = 761 MeV pedig a triplett-szingulett szeparáció. Az X_i mezőjárulék fejezi ki a kölcsönhatási mező és a kötési energiák hatását a mezonok tömegére. A 29 mezon tömege alapján illesztjük az 5 renormálási tömeget és a 3 nullától különböző X_i  mezőjárulékot (az u és d kvarkoknál ezt nullának vesszük), amit még kiegészít a J érték, összesen tehát 9 paramétert illesztünk a 29 tömegadat felhasználásával, ami lehetővé teszi, hogy a nyert paraméterek elég megbízhatóak legyenek, a számított és mért tömegadatok egyezése pedig jelzést ad az alkalmazott eljárás helyességére is.  Ez utóbbit mutatja, hogy a számított értékek hibája minden mezonnál 2 százalék alatt van, a relatív hibák szórása pedig 0,84 %. Létezik azonban két olyan η mezon, melyekre nem alkalmazható a fenti formula. Ugyanis a standard modell valamennyi hadront egy-egy kvark konfigurációval ad meg, kivéve a két η mezont, amit két különböző kvark kombináció szuperpozíciójaként azonosít, ahol az egyik ss típus, a másik u és d kvarkból, illetve antikvarkból tevődik össze. A formulát az ss típusra alkalmazva olyan tömeget kapunk (695 MeV), amely épp a két említett mezon tömege közé esik. Megjegyezzük, hogy az egyetlen hiányzó cb típusú triplett mezonra a számítás 6334 MeV tömeget ad, ezért érdemes lehet a nagyenergiájú kísérletekben ezt az energiatartományt vizsgálni a hiányzó részecske azonosítása érdekében.

Az illesztési eljárással kapott renormálási tömegeket, az X_i mezőjárulékot és a később tárgyalt barionok Y_i mezőjárulékait a 4. Táblázat mutatja:

4. Táblázat: A kvarkok renormálási tömege és mezőjárulékai MeV egységben

A barionok tömege

A 4. táblázatból látható, hogy az általunk számított renormálási tömegek jóval nagyobbak, mint amit a Standard Modell alapján meghatároztak a lineáris összegzési szabály alapján. A különbség különösen nagy a két „alap kvark”, azaz u és d esetében. Az irodalmi értékek szerint csupán 1 százalékot tesz ki a nukleonok tömegéből a renormálási tömeg, míg esetünkben a renormálási tömegek mintegy 20 százalékát adják a részecske tömegének.

A kvark modell összesen 75 barion felépítését teszi lehetővé, amiből 35 a kvartett és 40 a dublett, viszont 16-16 ilyen részecskét nem sikerült megfigyelni, ezért jelenleg 43 részecske tömegadata ismert. A barionok elnevezésére a proton (p) és neutron (n) mellett a Λ, Σ, Ξ, Ω szimbólumokat használják és az indexek utalnak a töltésre, spinre és a kvarkösszetételre. Barionok esetén a következő formulát javasoljuk a tömegek meghatározására:

Itt az m_i renormálási tömegek azonosak a mezonok segítségével meghatározott értékekkel. Az f együtthatóval vesszük figyelembe, hogy a két dublett kvark konfigurációban a tömegkülönbség arányos a teljes részecske tömeggel, az illesztési eljárásban  f = 0,976 az alsó és f = 1 a felső dublett esetén. Az Y_i mezőjárulékok határozzák meg, hogy mennyivel kell kiegészíteni a renormálási tömegeket az egyes kvark konfigurációkban és J_b = 742 MeV a kvartett-dublett szeparáció, ennek együtthatója n =1 a kvartett és n = 0 a dublett barionok esetén. Ez összesen 7 újabb paraméter illesztését jelenti a 43 tömegadat felhasználásával, tehát ismét lehetőség nyílik az alkalmazott eljárás helyességének ellenőrzésére. Az illesztéskor kapott Y_i értékek a 4. táblázatban szerepelnek. Az illesztés jóságát mutatja, hogy a legnagyobb relatív eltérés a 43 barion esetén csak 2,7 %, a relatív hibák szórása pedig 1,53 %. Ez a hiba lényegesen kisebb, mint amit lineáris összegzés esetén lehet kapni. Az eljárással meg lehet határozni a 16-16 ismeretlen barion tömegét is. A legnagyobb tömeg a bbb konfigurációjú kvartett bariontól várható: 12980 MeV. 

Összefoglalás

Összegzésként megállapíthatjuk, hogy a speciális relativitáselmélet kovariáns energia formulája alapján feltételezett négyzetes összegzési szabály valamennyi hadron esetén jól alkalmazható a részecskék tömegének meghatározására, ami jó alapot teremt az eddig nem detektált részecskék azonosítására is. A kvarkok renormálási tömege viszont lényegesen nagyobb, mint amekkorát a Standard Modell javasol az energiatagok lineáris összegzése alapján.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

SZESZEGO:

 Jól értem? A neutrínó anyag is meg nem is? Nincs is tömege és van is. Tömege először nagyon kicsinek tűnik, valójában nagyon nagy, csak a szokásos módon számunkra nem érzékelhető. Azért nem érzékelhető, mert a két kiralitás egymást fedi? (Mint a két kéz egymáson?) Abból ered a "kicsi" tömeg, hogy nem tökéletesen fedi egymást a két kiralitás? (Ennek a matematikai leírása az, hogy a diagonális értéke nulla?) Vagy az előző megállapítás csak érzékeltetés? Vagy a "kicsi" tömeg csak feltételezés, mert nélküle nem tudja a fizika értelmezni a gravitációt? De az utolsó mondatod szerint a gravitációból van a sötét anyag (nem értem, miért nem a tömegéből? Vagy a kettő - mint ahogy mondod - ikertulajdonság, tehát mindegy, melyikre helyezed a hangsúlyt? Vagy mégsem mindegy? A neutrínó olyan "antianyag", ami csak kicsi kölcsönhatásban van az anyaggal, tehát egymást nem semmisítik (?) meg?

Itt az olvasó türelmét kérem, mert nekem, mint Mórickának, mindenről a pénz jut eszembe. Valahogy így: a pénzt is két ellentétes irányú forgás hozza létre: a tartozás, az adósság (mint a váltó, vagy a pénz, ami a bank adóssága) forog az egyik irányban, és az áru (vagy amiért fizetnek) forog a másik irányban. Ellentétes irányú mozgása van  annak, amiért fizetnek, és annak, amivel fizetnek.  Azt azonban látni kell, hogy a pénz is adósság, és ha az adósság forog, akkor már nem a felek közötti adósság az, ami fizetési eszköz, hanem a pénzkibocsátó adóssága a fizetési eszköz. A pénz tehát olyan adósság, amellyel követelést lehet támasztani..  Hogyan lehetséges, hogy adóssággal követelést lehet teljesíteni? Úgy, hogy a követelést fizetésként elfogadják. Tehát a pénzben az adósság és a követelés, két ellentétes irányú mozgás: egymásba csúszik, egymást fedik. Ezt pedig a pénz gyors forgása teszi lehetővé, forgása egy olyan térben, melyet az adósság és a követelés kölcsönhatása, annak energiája képez. A pénz ettől lesz általános  adósság és egyúttal általános követelés (tehát az egyedi adósság még nem pénz). A pénz a kölcsönhatás energiája. Tehát nem egyedi ügyletben keletkezik, hanem az egyedi adósság ügyletek és azok kölcsönhatás terének egymásra hatásában. Ezért értéke mindig viszonylagos.  A pénz tehát a kölcsönhatás (vagy ahogyan korábban hangsúlyoztam, egy viszonynak) terméke. Maga tehát mindkét oldalt: a tartozást és követelést is képviseli: mintegy a két forgásirány a pénzben egyaránt képviselve van

Továbbá a pénznek forognia kell, ami két dolgot is jelent. A forgásnak van sebessége (pénz forgási sebessége), ami a pénz energiájára utal. Másrészt a forgást a körkörös mozgás jellemzi, tehát a pénz pályájának egyik meghatározó tulajdonsága az, hogy az adósságnak vissza kell térnie a kiindulópontjára, a körnek zárulnia kell. A pénz lezárja a kölcsönös követeléseket, és magának mint adósságnak is le kell zárulnia: a  bank által kibocsátott pénzt (banki adósság) banki követeléssel fedezni kell. Vagyis a bankok adósságot bocsátanak ki, és ehhez keresik a fedezetet (például a hitel révén keletkező követelést). (Azaz a kiinduló pont az adósság).  A pénz keletkezése, adósság (lásd váltó, kötvény, az állam adóssága, a bankadósság) a pénzrendszer motorikus eleme és nem a követelés.  Egy biztos: a rendszer domináns eleme az adósság és nem a követelés. Az adósság az, ami az emberi lét alapvető viszonya: adósai vagyunk a teremtésnek, a természetnek, a közösségeinknek, nemzetemnek, családomnak. A hajtóerő az adósság, annak teljesítése. A követelés pedig csak torz civilizációban válhat dominánssá. Ráadásul úgy történhet meg ez, hogy a bankok jelennek meg a teremtés (és ezáltal a pénzteremtés) intézményeként. Ekkor a domináns a banki követelés lehet, az alávetett az adós. A viszony ezzel a feje tetejére áll.

A két ellentétes irányú mozgás szemléltetése:

A pénz és az árú ellentétes irányú forgása

                                        Az árú útja:                                              A váltó, a pénz útja:

                                  Jobb forgásirány                                                Bal forgásirány 

                                         ⇒  ⇓                                                                ⇓   ⇐

                                         ⇑   ⇐                                                                ⇒  ⇑

 Az adósságról szóló elismervény visszakerül :

fizetségként, követelésként (például hitelnyújtás formájában) az adóshoz, a bankhoz.

A KÖR ZÁRUL ÉS ÚJRA NYÍLIK