A IV. rész folytatása
Az s típusú pályák külső módusa hasonló lefutást mutat a mostani ábrával. Ennek oka az aszimptotikus megoldás azonossága, ami a nagy r értékeknél dominál. Az s pályák esetén a radiális módusok száma megegyezik a fő kvantumszámmal, míg az l = n–1 pályáknál csak egyetlen radiális módust láthatunk. Valójában a fő kvantumszám mindig azonos a módusok számával, csak a módusok száma másképp oszlik meg radiálisan és a θ, ϕ polárszögek mentén. Az l > 0 esetben a gömbfelületeken l számú módus alakul ki, míg a radiális módusok száma n – l lesz. A pályák eltérése a gömbszimmetriától n – l értékétől függ, az l = n–1 pályáknál, ha n nagy már elhanyagolható az eltérés. Ez azt jelenti, hogy nagy kvantumszámok esetén a kvantummechanikai pályák egyre kevésbé különböznek a Bohr modell körpályáitól. A Bohr modell az energiát meghatározó n kvantumszámot az impulzusmomentumból származtatta, evvel szemben az energia az itt bemutatott közelítésben nem rendelhető valamilyen impulzusmomentum értékhez, hanem a módusok száma által meghatározott fő kvantumszámtól függ. Ez arra utal, hogy a módusok járuléka az energiához azonos a radiális- és a polárkoordináták esetében. A kísérleti tapasztalatok szerint az energia, ha kisebb mértékben is, de függ az n fő kvantumszámon kívül az l mellék kvantumszámtól is. Ennek oka az itt nem tárgyalt spin-pálya kölcsönhatás, ami a relativisztikus Dirac egyenletből származtatható.
Az atomok elektronjai fotonok abszorpciójával és emissziójával kerülhetnek át az egyik pályáról a másikra. Ennek kiválasztási szabálya analóg az oszcillátorokéval, de ebben az esetben az x változó helyett az r vektor jelenik meg az átmeneti valószínűség kifejezésében.
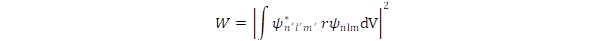
A kiválasztási szabály az Yl,m(θ,ϕ) gömbfüggvények szimmetria tulajdonságaiból következik Páros l esetén az origóra való tükrözés a függvényt önmagába viszi át, míg páratlan esetben megfordítja az előjelet. Tükrözéskor az r vektor előjele szintén megváltozik, ezért ha két azonos párosságú függvény szerepel az integrálban, akkor nulla lesz az átmeneti valószínűség. A gömbfüggvények további tulajdonsága, hogy szintén eltűnik az integrál, ha, l és l’ eltérése nagyobb egynél, azaz a kiválasztási szabály l→l±1 . Ez azt jelenti, hogy az elektront lehet gerjeszteni az 1s pályáról 2p-be, de nem lehet a 2s pályára. A tiltás azonban itt sem teljes, mert kisebb valószínűséggel a tiltott átmenetek is gerjesztődnek, aminek valószínűségét megkapjuk, ha a fenti integrálban r helyett annak négyzetét tesszük. Ily módon lehetőség van rá, hogy az alapállapotból kiindulva a fotonok tetszőleges gerjesztett állapotba vigyék több lépcsőn keresztül az elektront.
Fölvetődik a kérdés, ha az l = 0 pályák esetén centrumon áthaladó oszcillációs mozgás van, akkor hogyan lehet az s pálya gömbszimmetrikus? A kérdés elvezet a kvantummechanika sajátos szemléletmódjához. Gömbszimmetrikus potenciáltérben nincs kitüntetett irány, ha viszont olyan kölcsönhatás jön létre az elektron és a környezete között, ahol már szerepet játszik valamilyen irány, akkor már az elektron mozgása nem írható le gömbszimmetrikus pályával. Egyenleteink valójában olyan állapotra vonatkoznak, amikor az elektron nincs kölcsönhatásban a megfigyelővel. Fölösleges viszont olyasmiről beszélni, ami nem figyelhető meg! A kvantummechanika ezt úgy veszi tudomásul, hogy az összes lehetséges oszcillációs irányt számításba veszi, és erre átlagol. Ezt fogalmazza meg a szuperpozíciós elv, amikor úgy építi fel az állapotfüggvényt, hogy valószínűségi amplitúdókkal szorozza és összeadja a lehetséges állapotokat.
A stacionárius állapotokat leíró hullámfüggvény nem tartalmaz időbeliséget, ennek ellenére nyerhetünk bizonyos információt a részecske sebességéről. Kötött állapotban az irányfüggő sebesség átlagértéke csak nulla lehet a centrumhoz kötött koordinátarendszerben, viszont a sebesség négyzetének átlaga már nem nulla és ez jelenik meg a kinetikus energiában. A kinetikus energia abszolút értékben egyezik a kötési energiával, ezért az alapállapotban használhatjuk az E1 = ½m.e4/ℏ2 = ½p2/m összefüggést, amiből a sebesség abszolút értékének átlagára u = p/m = e2/ℏ értéket kapunk. Hasonlítsuk össze ezt az átlagsebességet a fénysebességgel:
u/c = e2/(ℏ.c) = α
Ez az arány a Sommerfeld féle finomszerkezeti állandó, értéke kerekítve 1/137, tehát egy kis szám, ennek köszönhető, hogy az elektronok mozgására jó közelítést ad a nem-relativisztikus Schrödinger egyenlet. A relativisztikus korrekciók mértékét a finomstruktúra állandó adja meg, amiért a vonalszerkezetben finom felhasadás jön létre. Innen származik az α konstans elnevezése is.
Az elektronátmenetek kiválasztási szabályai
Az elektromágneses kölcsönhatás alapja a töltött részecskék képessége, hogy fotonokat bocsátanak ki, vagy abszorbeálnak, amikor energiájuk és mozgási állapotuk megváltozik. Ez a képesség arra vezethető vissza, hogy a királis kettős forgások elindíthatnak, vagy elnyelhetnek egy-tengelyű forgásokat. A forgás beindításához az energián kívül szükség van impulzusmomentumra is. Ennek egyik módja, hogy az atomok és molekulák elektronjai az egyik stacionárius állapotból átugranak egy másikba, miközben impulzusmomentumuk ћ értékkel változik, például az atomban egy gerjesztett p állapotú (L = 1) elektron átmegy egy s állapotba (L = 0). Hétköznapi életünkben ennek vagyunk a tanúi, amikor látjuk a fénnyel telített világot. Ezek az átmenetek a látható és az UV tartományba esnek.
A másik fontos sugárzási forrás a molekulák atomjainak vibrációs rezgése. Itt is a töltések a sugárzás kibocsátói, mert az elektronok eloszlása a molekulában nem egyenletes és így lokális dipólusok alakulnak ki. A lineáris (longitudinális), vagy síkban történő (tranzverzális) rezgés azonban nem rendelkezik impulzusmomentummal. Miért jön létre mégis elektromágneses sugárzás? Ennek magyarázatát a fotonok szuperpozíciója adja meg. Két azonos frekvenciájú, ellentétesen polarizált foton létrehoz egy síkban polarizált állapotot, ahol a síkot a két foton fáziskülönbsége határozza meg. Amikor a vibráció az egyik állapotból a szomszédos állapotba ugrik, akkor olyan foton párt bocsát ki, melynek eredő impulzusmomentuma nulla. A vibrációs kvantumszám eggyel való megváltozása felel meg az elektron állapotváltozásánál megállapított ΔL = 1 kiválasztási szabálynak. A vibráció által kiváltott sugárzás az infravörös (IR) tartományba esik, és ez közvetíti a hőenergiát is.
Páratlan számú elektront tartalmazó molekulák nullától különböző S eredő spinnel rendelkeznek és alapállapotuk 2S+1-szeresen degenerált, például ha S = ½, akkor kétszeres a degeneráció foka. Ez a degeneráció bármilyen molekuláris szimmetria esetén fennáll, amit Kramers az időtükrözéssel szembeni szimmetriára vezetett vissza. A mágneses mező viszont megtöri az időtükrözés szimmetriáját, mert a köráramok forgásiránya határozza meg a kölcsönhatás előjelét. Ezért mágneses mezőben a degeneráció megszűnik, a felhasadt nívókhoz az Sz komponenshez tartozó M = ½ és -½ kvantumszámot rendelhetjük hozzá. A két állapot impulzusmomentumának térirányú komponense a ħ Planck állandóval különbözik, ami lehetővé teszi, hogy a g.μ_B.B = ℏ.ω rezonancia feltételnek megfelelő sugárzással átmenetet indukáljunk a két állapot között. Itt a g-érték a molekula elektron állapotától függ, ami megadja az elektron mágneses momentumát a μB Bohr magneton egységben. Ez az elektronspin-rezonancia (ESR) alapelve. Spinnel rendelkező atommagok esetén is hasonló rezonancia hozható létre (NMR vagy mag-mágnesesrezonancia). Az elektron mágneses momentuma három nagyságrenddel nagyobb a magokénál, ezért amíg az ESR tipikusan a mikrohullámú frekvencia tartományban, az NMR a rádióhullámú tartományban működik.
Az ESR kivételével a felsorolt példákban az elektron belső mozgási állapota változatlan marad, csak az elektromágneses mezőben való pályája változik meg. Az atommagokban és azok alkotórészeiben (nukleonok és kvarkok) vannak olyan állapotváltozások is, amikor a töltött részecskék belső mozgásának változása váltja ki az elektromágneses sugárzást, ehhez nagy energia tartozik, amit gammasugárzásnak nevezünk. Az említett folyamatok közös jellemzője, hogy a töltés, azaz a kettős forgás kiralitása nem változik meg a bomlás során. További példa nagy energiájú gammasugárzás keletkezésére, amikor részecskék és anti-részecskék ütközésekor annihiláció következik be. Ebben a folyamatban már az egyes részecskék töltése megszűnik, de a részecske pár eredő töltése továbbra is változatlan marad.
Összefoglaló gondolatok
Ebben az ötrészes bejegyzésben arra kerestük a választ, hogy mi az eredete a diszkrét energia nívók megjelenésének atomi rendszerekben. Külön vizsgáltuk a molekula vibrációkat atomok között és az elektronpályákat az atommag centrális erőterében. A klasszikus fizikai közelítés mindkét esetben folytonosan változó energiájú mozgásokra vezet, szemben a kísérleti tapasztalatokat jól leíró kvantummechanikával, ahol a kötött állapotok energiaszintjei ugrásszerűen változnak. A választ a fotonok kvantumos jellege adja meg, amelyek közvetítik az elektromágneses kölcsönhatást és rezonanciaszerű átmeneteket hoznak létre az oszcillátorok állapotában, illetve az elektronok impulzusmomentumát a Planck állandó mértékében változtathatják meg. A kvantumosság eredete ezért a fotonokhoz kapcsolódik, melyeknek impulzusát, impulzusmomentumát és energiáját a fénysebességű forgás hozza létre, amit viszont a térgeometria torzulása stabilizál az erős gravitáció révén.
Érdemes még rámutatni egy másik analógiára az oszcillátorok és a kötött pályán lévő elektronok között, amit úgy fogalmazhatunk meg, hogy a mikro-rendszerek nem lehetnek nyugalomban. Oszcillátoroknál ez a zéruspontrezgésben nyilvánul meg, elektronoknál pedig abban, hogy az elektron nem fogható be az atommagba. A jelenség a határozatlansági relációval magyarázható, hiszen mozdulatlan állapotban nulla lenne a pozíció és az impulzus is, ami ellentmond a bizonytalansági elvnek. Az oszcillátorok ekvidisztans energiaskálájának indulópontja a fél energiakvantum. Az atomi pályák kvantálási szabályát a pálya-impulzusmomentum határozza meg, ami alapállapotban nulla. Viszont az elektron rendelkezik ħ/2 spinnel, ezért itt is az alapállapothoz épp egy fél kvantum tartozik.
De minek köszönhető, hogy a kvantummechanika már magában foglalja azokat a törvényeket, amelyek végül is a fotonok tulajdonságaira épülnek? Ennek oka a fizikai operátorok megválasztása, amelyek mértékét a fotonok energiája, impulzusa és impulzusmomentuma határozza meg a ℏ Planck állandón keresztül.
A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"