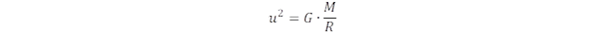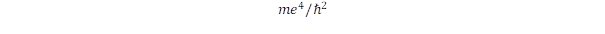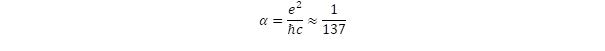A koldus és királyfi története, avagy hogyan érthetjük meg a mikrovilág titkait?
Mark Twain után szabadon
Hétköznapi világunkban minden pillanatban információk milliárdja ér el minket érzékszerveinken keresztül. Ezeket összesíti és dolgozza fel agyunk, így alakul ki fogalmi rendszerünk térről és időről, mozgásról, pályákról, az ok és okozat kapcsolatáról, véletlenről, determinizmusról, sőt még saját magunkról is, ha meg akarjuk fogalmazni, hogy mik vagyunk, mi a szerepünk és hogyan kapcsolódunk környező világunkhoz és embertársainkhoz is. Fogalmaink azonban nem hordoznak abszolút értelmet, mert attól az információs közegtől függenek, amelyre vonatkoznak.
Néhány alapfogalom eredete
Nézzünk meg néhány alapfogalmat, melyek számunkra olyan természetesnek tűnnek, például hogyan alakul ki tudatunk önmagunkról, miért gondolhatjuk úgy, hogy létezésünk elkülöníthető a környező világtól? Amikor látjuk a különböző tárgyakat, úgy érzékeljük, hogy tőlünk függetlenül léteznek és az a kölcsönhatás, ami köztünk van – első sorban a látás – nem változtat meg sem minket, sem a tárgyakat, vagy egyéb objektumokat. Ezáltal elválaszthatónak gondoljuk magunkat környezetünktől és úgy tekintünk a környező világra, hogy megismerhető, mert ismételt megfigyelések után is ugyanazokkal, vagy nagyon hasonló tulajdonságokkal találkozunk. Szemléletünk alapjává nem az válik, hogy a világ részei vagyunk, hanem az, hogy a világot kívülről, objektív módon szemléljük. A megismerhetőségről vallott felfogásunk onnan ered, hogy a köznapi megfigyelésekben úgy tűnik, mintha folytonosan és a tér tetszőlegesen közeli pontjaiból érkezne az információ a fotonok közvetítésével. Ez alapján felépítjük az objektíven – tehát tőlünk függetlenül – létező folytonos tér és idő fogalmát, és ok-okozat összefüggő láncaként írjuk le a történéseket, amit a determinizmus ural. De mennyire tarthatók fent ezek a megállapítások és fogalmak, amikor a mikrovilág titkait kutatjuk? Onnan csak akkor kapunk jelzést, ha egy elektron az egyik állapotból a másikba ugrik és kibocsát egy fotont, amit detektálhatunk. Két ugrás között nincs információnk az atom állapotáról, az információ érkezése már nem lesz folytonos. Ha mi küldünk valamilyen sugárzást az atomi objektumra, akkor annak állapota megváltozik, tehát méréstől való függetlenségről nem beszélhetünk. Nyerhetünk-e ilyen körülmények között egyáltalán objektív információt, beszélhetünk-e folytonos térről és időről? A helyzet a koldus és a királyfi viszonyához hasonlítható, Mark Twain regényében a gazdag környezetben felnövő királyfi állandóan konfliktusba kerül a szegények világával, amikor odakerül, mert magával hozott fogalmi rendszere ütközik a koldusokéval. Mi is hasonló helyzetben vagyunk, amikor az információ bőség birodalmából látogatást teszünk az információ szűkösség mikrovilágába, mert nem vagyunk képesek hátrahagyni megszokott fogalmainkat. Ez az eredete a mikrovilágról alkotott felfogásunk paradoxonjainak.
A komplexitás szintjei
Az információ gazdagság szempontjából kulcselem a komplexitás, nézzük meg először ennek nagyságrendi viszonyait. Mekkora is egymilliárd, ezt le tudjuk írni számainkkal, de már olyan nagy ez a szám, hogy elképzelni nem igazán tudjuk. Most induljunk ki ebből a számból, hogy osztályozni tudjuk nagyságrendi viszonyainkat. Vegyük „lazán” ezt a számot, ami lehet akár tízszer kisebb, vagy nagyobb is. Amikor valamiből egymilliárdszor több van, ezt nevezzük eggyel magasabb szintnek és ezekkel a szintekkel skálázzuk be világunkat.
Galaktikánkban hozzávetőleg egymilliárd csillag van, így a Tejút teljes tömege egy szinttel nagyobb Napunknál. De a galaktikák száma is a csillagászati felmérések szerint egymilliárd körül van, így a Nap és az univerzum között már két szint a különbség. De mekkorák vagyunk mi emberek, mennyivel vagyunk kisebbek, ha a Naphoz viszonyítjuk magunkat? Ekkor a milliárdot már harmadik hatványra kell emelni, azaz három szinttel vagyunk lejjebb. De viszonyítsuk magunkat az atomokhoz! Tömegünk az atomokhoz képest három szinttel, azaz millárdszor – milliárdszor - milliárdszor nagyobb. Kiindulhatunk a méretekből is, az atomok nagysága bő milliárddal kisebb nálunk, figyelembe véve a három dimenziót, ez is elvezet ahhoz, hogy három szinttel haladjuk meg a minket felépítő atomok méretét. Elmondhatjuk ezért, hogy a Naprendszernek éppen a középső mérettartományában vagyunk. Ha azt a kérdést vetjük fel, hogy hány atomból épül fel az univerzum, akkor már 3+3+2 = 8 „emelettel magasabb” az univerzum az egyes atomokhoz mérten. Ezen a kilencszintű skálán mi tehát a negyediken vagyunk. Ha a kilenc szint arányait el akarjuk képzelni, gondoljunk a következő sorra:
1. Atom
2 .DNS molekula
3. Egysejtűek
4. Ember
5. Emberiség
6. Óceánok
7. Nap
8. Galaxis
9. Univerzum
A természeti törvények hierarchiája
A méretbeli szintek lehetővé teszik rendkívül bonyolult struktúrák kialakulását. Az atomok kapcsolódásából felépülő magasabban struktúrák létezése magasabb szintű törvények megjelenésével társul, amelyek ugyan hasznosítják az alacsonyabb szintek törvényeit, de nem vezethetők le belőle. Képzeljük el, hogy néhány száz, esetleg ezer lego elemből különböző alakzatokat rakunk ki, például egy házat, egy autót, egy hajót, vagy tengeralattjárót, de kirakhatunk különböző állatokat, vagy emberi alakot is. Minden egyes alakzatnak megvan a maga szerkezeti törvénye, ennek kirakásához van egy tervünk, amely meghatározza, hogy végül mi lesz az alakzat, amit létrehozunk. Ez nincs kódolva az egyes lego elemekben, ezt már mi alakítjuk ki, csak az egyes elemek tulajdonságaival kell tisztába lennünk, hogy megfelelően tudjuk összekapcsolni az egyes részeket. Hogyan viszonyulnak ehhez a természet által megalkotott élőszervezetek? Nem megyek bele abba a kérdésbe, hogy az élet létrejötte a természet véletlen játéka-e, amely végigpróbálta a lehetőségek széles skáláját mielőtt létrehozta az életet, vagy a teremtő akaratról van-e szó. Induljunk ki a lehetséges struktúrák óriási számából! Hogyan kapcsolódik az élet kialakulása a fizika törvényeihez? Ennek is két szintjéből induljunk ki: a mechanika és a termodinamika törvényeiből.
Mozgási szabadsági fokok a mechanikában
Hogyan alkotta meg Newton a maga mozgástörvényét? Célja volt, hogy meghatározza egy mozgó objektum pályáját, amelyre erő hat. A makrovilág folytonosan érkező információjából indult ki, amely szerint pontosan tudhatjuk, hogy egy adott időben a megfigyelt tárgy éppen hol van, azaz a pálya tetszőleges pontossággal megismerhető. A pályát létrehozó törvényt a lehető legegyszerűbb formában akarta felírni, ami úgy érhető el, ha a mozgást apró elemekre bontjuk. Ez a felbontás végezhető el a differenciálás matematikai műveletével. A pályafüggvényt egyszer differenciálva jutunk el a sebességfüggvényhez, de ez még nem kapcsolható össze egyszerű módon az erővel, ezért egy második differenciálást is el kell végezni, amikor megkapjuk a gyorsulást. Ez már összekapcsolható az erővel, a Newton törvénye szerint a gyorsulás arányos az erővel, és megjelenik egy arányossági tényező is, amit tömegnek, tehetetlenségnek nevezünk: minél nagyobb a tömeg, annál nagyobb erőre van szükség, hogy ugyanakkora gyorsulást érjünk el. Ha most ismerjük az erőt, és tudjuk mekkora a tömeg, akkor meghatározhatjuk az objektumra ható gyorsulást is. De mi a pályára vagyunk kíváncsiak, emiatt integrálnunk kell, az első integrálás a sebességet adja meg, a második határozza meg a pozíciót, azaz eljuthatunk a pályához is. De van egy alapvető különbség a differenciálás és annak megfordítása az integrálás között. Ha ismerjük a pályafüggvényt, abból egyértelműen meghatározhatjuk differenciálással a sebesség és a gyorsulás lefutását, de integráláskor megváltozik a helyzet. A sebességfüggvény meghatározásához a gyorsulás mellett ismernünk kel a kezdősebességet, azaz a kezdő impulzust is. Ha el akarunk jutni a pályafüggvényhez, akkor belép egy újabb integrálási konstans, ekkor ismernünk kell a kezdeti pozíciókat is. Nagyobb rendszereknél, legyen szó akár egy egysejtű baktériumról, ez óriási számú kezdő paramétert jelent, mert minden egyes térbeli szerkezet még kiegészül az impulzus konfigurációk szabad megválasztásával, ami a milliárdszor milliárd lehetőség még egyszer milliárdszor milliárdféle megvalósulását jelenti. Az atomi mozgások törvényeit ugyan nem a Newton egyenletekkel, hanem a kvantummechanikával írjuk le, de ez nem befolyásolja a szabadsági fokok, azaz a komplexitás mértékét.
Az élővilág törvényei és a DNS-ben kódolt információ
Van-e valamilyen magasabb szintű törvény, amely szabályokba foglalja a hatalmas számú kezdőparaméter értékét? A fizika megad egyet a termodinamika révén, amely az entrópia fogalmán keresztül a változásoknak olyan irányt jelöl ki, amely szerint a rendezett struktúrák folytonosan csökkennek a rendezetlen mozgásformákhoz képest. Vannak azonban olyan „mintázatok”, azaz szabályszerűségek, amelyek a rendezettség elveit határozzák meg, ilyen rendezettségi elvet fogalmaz meg a zoológia és a botanika, amikor rendszerbe szedi a világ élőszervezeteit. Ezeket szabályszerűségeket kódolja az egymilliárd bázispárral rendelkező DNS molekulák rendszere. Hogyan kapcsolódik ez az említett kezdőparaméterekhez? Ezt nem tudjuk ugyan, de a paraméterek óriási száma ezt lehetővé teszi. Ahogy a lego nevű kirakós játékban az egyes elemek ismerete nem határozza meg a belőlük összerakható tárgyakat, ehhez kell egy „terv”, vagy „minta” amely megadja az egyes tárgyak összekapcsolási struktúráját, így a fizika is hiába ismeri az atomok összekapcsolási szabályait a kvantummechanika által, ebből még nem juthatunk el az élet törvényeihez.
A kétféle kezdőparaméter közül a pozíció határozza meg az egyes élőlények szerkezeti felépítését, amelynek szabályait a DNS molekula bázispárjainak sorrendje kódolja. Mennyi információt tárol a DNS molekula? Bináris rendszerként képzelve el 30 egység ad meg egy milliárd lehetőséget, ennek nyolcszorosa azaz 240 már akkora szám, ami megadja, hogy az univerzumban összesen hány atom van. De nem ennyi a bázispárok száma, hanem hozzávetőleg egy milliárd! Amíg a DNS kódolja az élő szervezetek felépítését, ami a pozíciók elrendezését jelenti, ott van még a szabadon választható kezdő impulzusok hatalmas rendszere. Ha keressük valahol a szabad akaratunk eredetét, akkor ezt ebben a kimeríthetetlen forrásban kell keresni és nem a kvantummechanikai bizonytalansági elvben.
Pályafogalom a makro- és mikrovilágban
A fentiekben használtunk bizonyos fogalmakat, de most nézzük meg, honnan származnak ezek a fogalmak, mennyiben kötődnek rendelkezésünkre álló információ mennyiségéhez? Vegyük például azt a fogalmat, hogy pálya, amikor egy fizikai objektum mozgásáról beszélünk. Legyen szó egy labdáról, vagy egy bolygóról, onnan minden pillanatban óriási számú foton érkezik szemünkbe, vagy a felvevő készülékbe. Ez alapján folytonosan tudjuk követni, hogy éppen hol van ez az objektum. Voltaképp erre alapozzuk a folytonos tér és idő fogalmát. Ez a folytonos szerkezet, amely matematikailag lehetővé teszi, hogy differenciálhatóságról beszéljünk. Ezek a fogalmak az információ milliárdos „királyfi” fogalmai. De most merüljünk alá a mikrovilágba! Láthatjuk-e például az elektront, nyomon követhetjük a pályáját? Ha egy gyorsítóból kilépő elektront vizsgálunk, akkor az emulzióban, vagy a ködkamrában láthatunk egy nyomot, amit a részecskének tulajdonítunk. Ez a nyom, ha elektromágneses térben történik a mozgás, lehetőséget ad bizonyos paraméterek – például a töltés, tömeg, impulzus – meghatározására is. Vajon ekkor egyetlen részecskétől származó információt hasznosítunk? Igaz ugyan, hogy egyetlen részecskére vonatkozó paraméterekről beszélünk, de valójában óriási mennyiségű információ segítségével érjük ezt el. Az elektron kölcsönhatásba lép az emulzió molekuláival és úgy alakítja át az ionizáció révén, hogy az fototechnikával láthatóvá tehető. Ez egyrészt azt jelenti, hogy mozgása közben az elektron nagyszámú molekulával ütközik, melyek során energiát veszít, de ennek mértékét elhanyagolhatónak vesszük. Továbbá, amikor „látjuk” a nyomot, az annak köszönhető, hogy az emulzió tanulmányozásakor hatalmas számú foton jut el szemünkbe. Az elektront tehát nem is látjuk, de elképzeljük és matematikailag leírjuk pályáját. Képzeletünk azonban a makrovilág nagyszámú információján alapszik, ekkor is „királyfiként” gondolkozunk.
A kvantum fogalmának megjelenése a mikrovilágban
De hogyan jutottunk el ahhoz a gondolathoz, hogy a mikrovilág fizikai törvényei nem folytonosak, hanem kvantumosak? Ehhez kellett találniuk valamilyen ellentmondást a különböző makroszkopikus és folytonosságra építő fizikai elmélet között. Ez az ellentmondás a fekete test sugárzási törvényénél bukott elő. Ha felizzítunk egy testet, akkor sugározni kezd, és minél magasabb a hőmérséklet, annál „fehérebb” a kisugárzott fény. Ez azt jelenti, hogy a kis energiájú, hosszú hullámú sugarak száma csökken, a magasabb frekvenciájú sugarak száma nő, intenzitásuk elér egy maximumot, majd a látható fényen túli UV tartományban csökkenni fog az intenzitás. A magas frekvenciájú tartomány viselkedését jól lehetett értelmezni a termodinamika törvényeivel, de ellentmondás jött létre a kisebb frekvenciák esetén. Ott az elmélet egyre nagyobb intenzitást kalkulált a frekvencia csökkenésével. Honnan származott ez a következtetés? Onnan, hogy az elektromágneses sugárzást a klasszikus elmélet folytonos paraméterekkel írta le, és emiatt egy adott frekvenciájú sugárzás energiája tetszőlegesen kis értékű is lehetetett, ami a termodinamika partíciós törvénye miatt növekvő intenzitást eredményezett a frekvencia csökkenésével. A gordiuszi csomót Planck vágta át, amikor a XX. század fordulóján feltételezte, hogy az f frekvenciájú sugárzásnak van egy legkisebb adagja, amelyhez E = h·f energia tartozik. Itt a h konstans, amely az energia és a frekvencia hányadosa, impulzusnyomaték dimenziójú mennyiség és az ebből képzett redukált ℏ = h/2 Planck állandó a fény legkisebb adagjának – azaz a fotonnak – az impulzusnyomatéka. Tehát a fény is hordoz impulzusnyomatékot. Ezt a fogalmat a klasszikus mechanika mint folytonosan változó mennyiséget definiálja, de Planck szerint a fénynél ez ugrásokban változik. Ez volt a fizikának az a pillanata, amikor a démokritoszi atom koncepciót teljesen magáévá tette. Korábban a kémia eredményei világossá tették, hogy minden fizikai elemnek van egy legkisebb egysége: az atom, és ezekből az építőkövekből épülnek fel a kémiailag hasonlóan viselkedő molekulák. Planck felfedezése ezt avval egészítette ki, hogy a fény is „atomos”, azaz elemi részecskékből, fotonokból áll.
Az atom fogalma is átalakul
A fény frekvenciájáról is kiderült, hogy nem változik folytonosan. Gőztérben az atomok – például a hidrogén – sugárzását vizsgálva diszkrét vonalakat lehetett megfigyelni. Ennek okát a radioaktivitás felfedezése tárta fel, amelyből kiderült, hogy amit a kémia atomnak tart az is tovább bontható, mégpedig atommagra és elektronokra. A bomlás során kibocsátott háromféle sugárzás (alfa, béta és gamma) közül a bétasugárzás nem más, mint az atomokból kilépő elektron, ami az elektrodinamikában a töltés legkisebb egységét adja. Tehát az elektrodinamika töltés fogalmáról is kiderült, hogy nem folytonosan változó fizikai mennyiség. Az alfasugárzás viszont pozitív töltésű és megfelel az elektronjaitól megfosztott hélium atomnak, míg a gammasugarak nagyenergiájú elektromágneses sugarak.
A Bohr modelltől a kvantummechanikáig
Az összetett szerkezetű atomot Bohr miniatűr naprendszerként képzelte el, ami érthető, hiszen ő is a makroszkopikus fogalmi rendszer alapján próbálta megérteni a mikrovilágot. Körpályákon keringő elektronokat feltételezett az atommag körül, ahol a centrifugális erőt a pozitív atommag és a negatív elektron közötti vonzóhatás egyenlíti ki. Igen ám, de ellentmondásba került az elektrodinamika törvényeivel, mert a keringő töltés állandóan elektromágneses sugárzást bocsát ki az elektrodinamika szerint, ez pedig az elektron energiájának elvesztését okozná. De Bohr elég bátor gondolkodó volt, hogy megtegye az első ösztönös lépést a makrovilágból a mikrovilág fogalmai felé. Feltételezte, hogy az elektronnak vannak stacionárius állapotai, amikor nem sugároz és ezeket az állapotokat az impulzusnyomaték egységéhez – a redukált Planck állandó egész számú többszöröséhez – rendelte, és a fényspektrum diszkrét vonalait úgy fogta fel, mint ugrásokat a stacionárius állapotok között. Evvel két „legyet ütött” egy csapásra, mert elméleti magyarázatot kapott a kísérletileg mért diszkrét frekvencia értékekre, és kapcsolatot talált az elektron keringéséhez és a fotonhoz tartozó kvantált impulzusnyomaték között.
A hidrogénatom színképét lehetett Bohr modelljével magyarázni, de az elv már nem működött nagyobb rendszámú atomoknál, ahol több elektron is jelen van. Szükség volt ezért egy átfogó elméletre a mikrovilág mechanikájának leírására. Ezt alkotta meg egymástól függetlenül Schrödinger és Heisenberg. A két elmélet látszólag különbözik, de később kiderült, hogy azonos eredményre vezetnek, csak matematikai kiindulópontjuk volt eltérő. A kvantummechanika megértését az nehezíti, hogy a tankönyvek nem a fogalmi rendszerből, hanem a matematikai eszközök definiálásából indulnak ki. Mi kövessünk egy másik utat és próbáljuk elképzelni, hogyan gondolkozhatott Schrödinger nevezetes egyenletének kidolgozásakor.
A makrovilág fizikai fogalmainak átalakulása a kvantummechanikában
Erwin Schrödinger az atom elektronjainak pályáját akarta leírni. A pálya fogalmát a klasszikus mechanikában függvénykapcsolat írja le, melyben a térbeli helyzetet az idő függvényében adjuk meg, mégpedig minden egyes időponthoz pontos pozíciót rendelünk. A makrovilágban ezt megtehetjük, mert elvben végtelenül sűrű időközökben tudósítanak fotonok a test helyzetéről. Az atomi elektron tényleges mozgásáról viszont nem tudunk semmit, csak azt észleljük, amikor állapota megváltozik és kibocsát egy fotont. Emiatt a változásból kell arra következtetni, hogy milyen lehet a pálya, amikor nincs változás. Tehát az információ nem arra vonatkozik közvetlenül, amit meg akarunk ismerni. Minden pályához valamekkora energia tartozik, és a keresett állapotban az elektron energiája állandó. Mit jelent ez az energiára nézve? Értelmezzük úgy az energiát mint egy olyan hatást, amelyik az időben nem változtatja meg az elektron állapotát. Az állandóság matematikailag azt jelenti, hogy amikor az állapotot leíró függvényt idő szerint deriváljuk a függvény önmaga marad, eltekintve egy a függvény szerkezetét nem befolyásoló konstans szorzótól. Ez a konstans szorzó más és más lehet az egyes állapotokban, amit az energiához rendelhetünk. Evvel kaput nyitottunk diszkrét energiaértékek megjelenése felé. Matematikailag az idő szerinti deriválás végtelenül kis idő intervallummal való osztásnak felel meg, ez a művelet pedig az idő reciprokához, azaz frekvenciához vezet. Fotonok esetén a frekvenciát a h Planck állandóval szorozva az energiát kapjuk meg. Ennek mintájára tekinthetjük az energiát h/t alakú operátornak. A klasszikus mechanikából tudjuk, hogy az energia kinetikus és potenciális energiából tevődik össze, fogadjuk ezt el érvényesnek a mikrovilágban is. Azt is tudjuk a klasszikus mechanikából, hogy a kinetikus energia az impulzus négyzetének és a tömeg kétszeresének hányadosa. Nyúljunk továbbá vissza Newton első törvényéhez is, amely szerint erőhatás nélküli térben a testek megtartják egyenes vonalú egyenletes sebességű mozgásukat, ami azt jelenti, hogy az impulzus nem változik meg a helyzet változása során. Az impulzust ezért olyan hatásként értelmezhetjük, amely a térkoordinátákkal való deriválás során állandó marad. Ez a deriválás a határértékben végtelenül kis helyváltozással való osztást jelent, amely dimenzióját tekintve hullámhossznak felel meg. Ismét gondoljunk a fotonra, amely impulzussal rendelkezik, és ennek értékét a Planck állandó és a hullámhossz hányadosa adja meg, emiatt akkor maradunk összhangban a foton tulajdonságaival, ha az impulzus hatását a pályafüggvényre a h/x operátorral definiáljuk. Ha ez az operátor nem változtatja meg a pályafüggvény szerkezetét, csupán megszorozza egy konstanssal, akkor ezt a konstanst úgy tekinthetjük mint a mozgáshoz tartozó impulzust.
Korrespondancia a makro- és mikrovilág fogalmai között
Az előző gondolatmenet az összekapcsolás elvén alapul: amennyire lehet, megtartjuk a makrovilág fizikai fogalmait, például a tér és idő fogalmának folytonosságát, ugyanakkor arra törekszünk,hogy összhangban legyünk a kvantált foton tulajdonságaival is. Ez vezet el az olyan elmélethez, amely nem szakad el a nagyszámú elemből felépülő makroszkopikus objektumok törvényeitől, hanem harmonikusan összesimul vele. Ezt nevezi a kvantummechanika korrespondancia elvnek.
A kvantummechanikai állapotfüggvény fogalma
A kvantummechanikai képben a makroszkopikus pályafüggvény helyébe az állapotfüggvény kerül. De milyen fizikai tulajdonságnak felel meg az állapotfüggvény? Ez a kvantummechanikai értelmezések kulcskérdése! Mivel a stacionárius állapotban nem történik változás, ezért az idő fogalma – legalább is részlegesen – értelmét veszti. Többé már nem kérdezhetjük meg az információ hiányában (el kell hagyni a királyfi logikáját!), hogy éppen most hol tartózkodik az elektron, de helyette felvethető a kérdés, hogy hol lehet! A hol lehet kérdésre viszont a valószínűség a válasz: mekkora valószínűséggel tartózkodhat az elektron egy adott helyen. Az állapotfüggvény ezért alapvetően a valószínűséghez kapcsolódik, bár nem azonos vele. A különbségnek nagyon fontos szerepe van! Ha az állapotfüggvény abszolút értékének négyzetét képezzük, akkor eljutunk a valószínűséghez, de közben kiesik valami: az idő szerinti periodikus változás. Ez a látens időfüggés azért rendkívül fontos, mert ebben rejtve van a mikrorendszer azon képessége, hogy kilépjen a stacionárius állapotból, és ebben rejlik az interferencia jelenségek magyarázata is. A látens időfüggés segít megérteni a problémát, ami akkor merül fel, ha azt kérdezzük, miért éppen most következik az ugrás. Az időről szóló információ nélkül a kvantummechanika csak arra tud válaszolni, hogy mekkora valószínűséggel következik be a változás. Az idő fogalmaiban gondolkozó királyfinak át kell venni a koldus valószínűségi felfogását, mert a rejtett időbeli periodikusságról nem érkezik információ.
Az állapotfüggvény periodikussága és a fizikai operátorok imaginárius felépítése
Nézzük most az operátorok matematikai tulajdonságait! Az a függvénytípus, amely az idő illetve térkoordináták szerinti deriváláskor önmagába megy át az exponenciális függvény. Az exponenciális függvény argumentuma komplex szám is lehet, amelyben a valós rész időben, vagy térben növekedést, vagy csökkenést hoz létre, míg az imaginárius tag idő- illetve térbeli periodikusságot ír le. Az állapot időbeni állandósága állandó amplitúdójú hullámoknak felel meg, ezért a keresett függvények időbeli argumentuma tisztán imaginárius szám. Viszont az argumentum egyúttal az exponenciális függvény deriváltjának konstans szorzója:
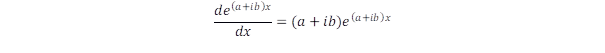 ,
,
amely a kvantummechanikában meghatározza a fizikai mennyiség értékét. A mérési eredmények azonban mindig valósak, amit úgy biztosíthatunk, ha az energia és impulzus operátora imaginárius lesz: azaz iℏ/t illetve iℏ/x. Ha a kinetikus energiában az impulzus helyébe a megfelelő operátort beírjuk, és egyenlővé tesszük az energia operátor kétféle alakját, megkapjuk a Schrödinger egyenletet. Ez a formalizmus nem csak a Bohr-féle elektronpályákkal ad ekvivalens leírást, hanem alkalmazható tetszőlegesen összetett mikro rendszerekre is.
A kvantum eredete és az impulzusnyomaték fogalmának átalakulása
Az elmondottal legfőbb tanulsága, hogy a kvantummechanikai formalizmus a foton tulajdonságaira épül. Ez mindenekelőtt az impulzusnyomaték definíciójában mutatkozik meg! Makroszkopikusan az impulzusnyomaték az impulzus fogalmának forgó- és keringő mozgásokra történő általánosítása. Forgás esetén az elemi tartományokra felbontott test impulzusát szorozzuk az egyes elemek forgási tengelytől mért távolságával és ezeket összegezzük, pontszerűnek tekintett objektum keringésénél pedig a test impulzusát szorozzuk a sugárral. Az impulzusnyomaték létezése két dolgot követel meg: egyrészt a test, vagy annak komponensei rendelkezzenek impulzussal, másrészt létezzen egy véges sugár a forgástengelytől mérve. A klasszikus fizikában ezek a mennyiségek folytonosan változnak, ezért az impulzusnyomaték is folytonosan változó mennyiség. De miért lesz az impulzusnyomaték kvantált a mikrovilágban, és egyáltalán honnan származik a foton impulzusnyomatéka? Erre a szokásos tárgyalásmód csak formális választ ad. Az impulzusnyomaték operátorát a klasszikus mechanika alapján adja meg, amikor az impulzus operátor és a sugár vektoriális szorzataként vezetik be, majd matematikailag kimutatják, hogy ennek az operátornak a sajátértékei – azaz a sajátfüggvény szorzási együtthatója – csak a redukált Planck állandó egész számú többszöröse lehet. Annak érdekében, hogy ne kelljen állandóan emlegetni a redukált Planck állandót vezetik be a spin fogalmát, amely azt a számot jelenti, amivel szorozzuk ℏ-át, amikor megadjuk az impulzusnyomatékot.
Folytatás : 2. rész: II. Hogyan igazodhatunk el a mikrovilág útvesztőiben?
A blog egyéb írásait összefoglalja és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés.