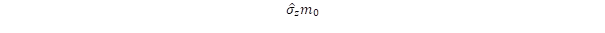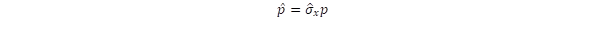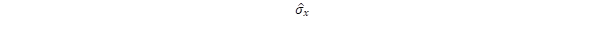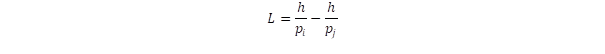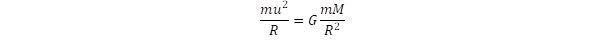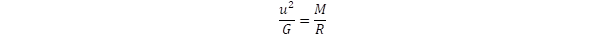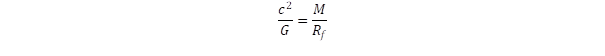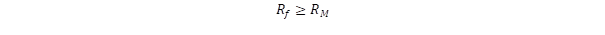Két évvel ezelőtt támadt az ötletem, hogy a tudományos kutatásban  szerzett tapasztalataimat és a fizikával kapcsolatos gondolataimat felteszem egy blogra, amihez  „A fizika kalandja” címet választottam.  Különösebb érdeklődésre nem számítottam, reméltem, hogy talán egy-két tucat ember olvasni fogja időnként, ezért meglepetés számomra, hogy immár a letöltések száma elérte a százezret. Az induláskor nem volt nagyobb forgalom, de egy év után valami történt, hirtelen két napra megugrott a letöltések száma, aztán visszaesett a szokásos szintre. Később még néhányszor megismétlődött az egy-két napos megugrás, mire felfedeztem ennek okát: a blogban közölt írásom felkerült az Index portáljára. Azóta ez rendszeressé vált, így nagyban hozzájárult a blog népszerűségéhez. Itt érdemes megjegyezni, hogy az index tudományos rovata színvonalasan tájékoztat népszerűsítő szinten a tudományok különböző kérdéseiről, ami dicséri szerkesztőinek szakmai felkészültségét és munkáját.

Jelentősebb érdeklődést kiváltó bejegyzések

A százezer letöltés és közel száz bejegyzés után már érdemes mérleget vonni és megnézni, hogy milyen kérdések iránt volt a legnagyobb érdeklődés és milyen kommentekkel reagáltak az írásokra az olvasók. Két írás iránt mutatkozott kiemelkedő érdeklődés, az egyik az ősrobbanás elméletével foglalkozott  egy lehetséges alternatívát felmutatva („Volt-e valójában ősrobbanás, vagy a fény sebessége lassul?”, 20 000 feletti letöltés, 240 komment), a másik a mikrovilág és a hétköznapi gondolkozás közötti szakadékról  szólt („A józanész kudarca a modern fizikában”, 16 000 feletti letöltés, 150 komment). Mindkét téma gondolkozásunk és a megismerés határait feszegeti. Az írások iránti érdeklődéshez hozzájárul, hogy a hivatalos tudomány által elfogadott felfogás mellett felhívja a figyelmet más megközelítések lehetőségére is. Jelentős érdeklődést váltottak ki a kvantumvilág rejtelmeit taglaló írások is („Az a titokzatos alagúteffektus, 7900 letöltés, „Hogyan hozhatunk létre teleportálást a kvantummechanika szerint”, 3900 letöltés). Meglepően sokan érdeklődtek olyan elméleti kérdés iránt is, hogyan lehet a klasszikus mechanikából elindulva eljutni a kvantummechanika fogalomvilágáig és megérteni annak matematikai formalizmusát („Út a kvantummechanika megértéséhez”, 1300 letöltés). Jelentősebb érdeklődés volt a hétköznapi jelenségek fizikai magyarázatával foglalkozó írások iránt is („Miért kék az ég? Mindennapi jelenségek fizikai magyarázata”, 3000 letöltés, „Rezgések, hullámok és rezonanciák”, 1700 letöltés, „Szimmetria jelenségek a mindennapokban és a modern fizikában”, 1000 letöltés).

Érdeklődést váltottak ki a gravitációs hullámokkal és az Univerzum kialakulásával foglalkozó írások is („A görbült tér víziója és a gravitációs hullámok”, 1600 letöltés, „Az univerzum korszakváltásai”, 2800 letöltés). A részecskefizika területén a neutrínókról szóló írásokat is sokan olvasták („Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók, 1000 letöltés, „A neutrínó kalandos története”, 1600 letöltés, Egyéb részecske fizikai kérdések is érdeklődést váltottak ki: „Nyomaték vagy momentum: kapcsolat a makrovilág és a mikrovilág között”, 1800 letöltés, „Miért dominál az anyag az antianyag felett”, 1000 letöltés.  

Milyen legyen egy tudományos blog?

Eddigi tapasztalatom szerint nem az aktuális tudományos szenzációkra kell rárepülni, az ilyen témákról eleget írnak a média különböző orgánumai. Ehelyett meg kell találni azokat a területeket, amit az emberek nem igazán értenek, de gondolkoznak rajta és időnként saját elképzeléseik alapján  próbálják magyarázni a vitatható jelenségeket. Mert a tudományban is vannak viták és baj az, ha a hivatalos tudomány felkentjei által kanonizált elméleteket nem szabad megkérdőjelezni. Az a tudomány halott, amelyik már fél az új gondolatoktól! De legalább ekkora veszély az áltudományok elburjánzása, ezért fontos közérthető módon a tudomány fényével átvilágítani a rejtélyes jelenségeket. A legnehezebb néha megmondani, hogy hol a határ a valódi tudomány, az ezotéria és az áltudományok között. Ha ebben segít ez a blog is, akkor érdemes volt hozzákezdeni.

A kommentírás szubkultúrája

A különböző bejegyzésekre erősen polarizált vélemények érkeztek. Mi készteti az olvasókat kommentek küldésére? A legtermészetesebb ok, ha valaki nem ért egyet a leírtakkal és rámutat valamilyen téves állításra, pontatlan megfogalmazásra. Ha ilyen érkezik, azt köszönettel veszem és korrigálom a leírtakat. Néhány kommentelő az internet anonimitása mögé bújva abban éli ki magát, hogy durva szavakkal teremti le a bejegyzések íróját, vagy aláz le egy másik kommentelőt. Az ilyen kommentek a küldőjüket minősítik. Mások azért küldenek kommenteket, hogy kifejezzék egyetértésüket a megfogalmazott gondolatokkal és elmondják, hogy milyen fontosnak és jónak tartják a blog írásait. Érkeztek egészen kitűnő és magvas kommentek is, taglalva a tudomány szerepét, a megismerés határait, vagy rámutatnak egyes tudományterületek sajátságaira, ezek igazolják leginkább, hogy érdemes volt megjelentetni egy-egy írást.

Hogyan tovább?

Meddig lehet, meddig érdemes folytatni egy blog írását? Előbb utóbb a témák kimerülnek, nehéz újabb ötleteket találni, amiről érdemes írni. Sokat segítene, ha mások is bekapcsolódnának, hogy közzé tegyék gondolataikat, vagy tapasztalataikat a tudomány valamelyik területéről. Ha ilyen anyagot kapuk szívesen vállalkozok az írások szerkesztésére és megjelentetésére.

A blog további írásaira hívja fel a figyelmet a „Paradigmaváltás a fizikában” című bejegyzés a linkek megadásával.

Az Univerzum kialakulásáról és fejlődéséről az ősrobbanás elmélete sok érdekes tényt tárt fel, de legalább annyi a kérdőjel is az elmélettel kapcsolatban. A korábbi bejegyzésben (Az Univerzum korszakváltásai) az elmélet legfontosabb eredményeit foglaltam össze, most viszont egy alternatív magyarázatra hívom fel a figyelmet.

Vöröseltolódás: az ősrobbanás elméletének kiindulópontja

Honnan is indult el az ősrobbanás elmélete? Ennek alapja a távoli galaxisok vöröseltolódása. Hagyományos csillagászati eszközökkel mintegy 70 millió fényév távolságú galaxisok távolságát sikerült megbecsülni. A 10 millió fényévnél nagyobb távolságú galaxisokból érkező fény spektrumvonalai (jelesül a hidrogén alfa vonala) eltolódik a vörös felé és ennek mértéke a távolsággal arányosan növekszik. Ha abból indulunk ki, hogy a fizika törvényei mindenütt azonosak, tehát még a milliárd fényévnyi távolságból érkező fénysugarak tulajdonságait is ugyanazok a fizikai állandók –  így a c fénysebesség és a h Planck állandó  – határozzák meg az Univerzum minden pontjában és minden időben. Továbbá az elemi részecskék tulajdonságai sem térnek el, mint például az elektron tömege és töltése, akkor a vöröseltolódás egyetlen magyarázata az lehet, hogy a távoli galaxisok távolodnak tőlünk és a távolodási sebesség arányosan növekszik a távolsággal. Ez a Hubble-törvény, amely a fény Doppler effektusán alapul. Ahogy a távolodó vonat füttye mélyül – úgy csökken a fény frekvenciája is – amit egy tőlünk távolodó objektum, például egy szupernóva, vagy kvazár bocsát ki. Ez utóbbi a vöröseltolódás, amelynek mértéke árulkodik az égitest hozzánk mért sebességéről.

Az ősrobbanás rendkívüli körülményei

A galaxisok nagy része azonban sokkal jelentősebb vöröseltolódással rendelkezik, mint amit az ismert távolságú galaxisoknál találtak, ezért adódott a következtetés, hogy ezek az égi objektumok már jóval távolabb vannak tőlünk, egyesek akár tíz milliárd fényév távolságra vannak. Ha azonban az Univerzum tágul, akkor a múltban kisebb volt, és ha elég távol megyünk vissza a múltba – ez a mai elmélet szerint 13,7 milliárd év – akkor az egész Univerzum egyetlen pont lehetett. Így jutunk el a Lemaître által megfogalmazott ősrobbanás elméletéhez. Az alapgondolat elképesztő következményekkel jár. Egyetlen galaxisban milliárd csillag van és a galaxisok ismert száma kétmilliárd körüli. Ennek hatalmas tömege és energiája egyetlen parányi pontba sűrítve! Micsoda hatalmas hőmérséklet és anyagsűrűség felel ennek meg! Ilyen körülmények között nem lehettek atomok és molekulák, sőt az atommagot alkotó protonok és neutronok sem maradhatnak fent, csak egy ősi plazma állapot, amelyben a kvarkok és gluonok kavarogtak. De a tágulás lehűtötte az Univerzumot, és amikor ennek során az atomok létrejöttek a fény kiszabadult az átláthatatlan plazmából és bevilágította a világot. Ennek nyomát figyelhetjük meg a kozmikus mikrohullámú háttér sugárzásban, amelynek megfigyelése az ősrobbanás elméletének legfőbb bizonyítéka.

Az Univerzum inflációja és a gyorsulva tágulás

Az ősrobbanás matematikai modelljét Friedman hozta létre felhasználva Einstein általános gravitációs elméletét. Ennek taglalásával foglalkozott a korábbi bejegyzés (Az Univerzum korszakváltásai). Az elmélet finomítása vezetett ahhoz a következtetéshez, hogy a távolodás sem egyenletes, hanem gyorsul a távolság függvényében. Fontos előrelépés volt, hogy az ősrobbanás korai szakaszában, a becslések szerint 10^-36 és 10^-32 másodperc között, az Univerzum a fénysebességét nagyságrendekkel meghaladó tempóban felfúvódott, ez az infláció jelensége. A modellt összevetve csillagászati megfigyelésekkel meghatározták az Univerzum sugarát is, amit 46,6 milliárd fényévre becsülnek. Ez azért meglepő, mert a 13,7 milliárd év alatt csak akkor növekedhetett meg ekkorára az Univerzum, ha a növekedés sebessége átlagban háromszorosa volt a fény sebességének. Ezt úgy értelmezik, hogy a speciális relativitáselmélet által szabott korlát csak az anyagi objektumok mozgására érvényes és nem a tér tágulására, amelyben a galaxisok elhelyezkednek.

A vöröseltolódás magyarázata a fénysebesség változásával

Ez volt idáig a jelenleg elfogadott ősrobbanás-elmélet ismertetése. De most tegyük fel a kérdést, vajon nem adhatunk-e más magyarázatot a vöröseltolódásra, vajon kizárólag a tágulási elmélet magyarázhatja a csillagászati megfigyeléseket? Már az ősrobbanás elmélete is elvezetett ahhoz a gondolathoz, hogy a kezdetekben a tágulási sebesség sokkal nagyobb volt, mint a fénysebesség. Kézenfekvőnek tűnik a feltevés, talán maga a fénysebesség sem állandó! Persze ez ellenkezik jelenlegi tapasztalatainkkal, amit a speciális relativitáselmélet vesz alapul, de ismereteink csak a földi körülményekre vonatkoznak és csak mintegy száz év megfigyeléseit összegzik. De mi volt milliárd évekkel ezelőtt? Nem könnyebb azt elképzelni, hogy akkor a fény sokkal gyorsabban száguldott, mint elfogadni, hogy az egész Univerzum egyetlen parányi pont volt? Ez a lehetőség elég kézenfekvő ahhoz, hogy megnézzük a feltevés következményeit. Ha a fénysebesség az időben változik, akkor ezt legkönnyebben egy exponenciális függvénnyel írhatjuk le, amely a messze múltban gyorsan növekedett, de napjainkban már a görbe kisimult. Jelöljük a mai fénysebességet c₀-al és egy T₀ időállandóval jellemezzük az exponenciális változást:

Az időállandó nagyságrendjét az ősrobbanás által javasolt 13,7 milliárd év adja meg, ezért T₀ legyen 10 milliárd év. Ez azt jelenti, hogy tízmilliárd évvel ezelőtt a fény sebessége a mostaninál 2,718-szor volt nagyobb. Határozzuk meg, hogy az így változó fénysebesség mekkora vöröseltolódást okoz!  Tételezzük fel, hogy a fénysebességtől eltekintve a többi természeti állandó nem változott az Univerzum fejlődése során, tehát azonos maradt a Planck állandó, az elektromos töltés és az elektron tömege is. Az atomok energiáját meghatározó állandó:

nem függ a fény sebességétől. Szintén független c-től az atom két állapota közötti ugrás frekvenciája, hiszen a fotonok energiája hν = E. A nagyobb fénysebesség miatt viszont megnövekszik a hullámhossz, hiszen λν  = c, azaz λ = c/ν. Abban a tartományban, ahol a Hubble-állandó meghatározása történik (maximum 70 millió fényév) a T/T₀ érték kisebb, mint egyszázad, amiért az exponenciális függvény  lineáris összefüggéssel közelíthető, azaz a vöröseltolódás mértéke arányos lesz a távolsággal. A lineáristól való számottevő eltérést az 1 milliárd fényév távolságú galaxisoknál kapunk, hasonlóan az ősrobbanás gyorsulva táguló Univerzumot feltételező koncepciójához.

Megfigyelhető-e vöröseltolódás a Tejút csillagainál?

Megfigyelhetjük-e a vöröseltolódást a Tejút csillagjainak fényénél? A Tejút sugara 100 ezer fényév, amiért T/T₀ nem nagyobb, mint 10^-5. Ezt a hatást azonban elfedi a csillagok illetve a Föld mozgása miatti Doppler effektus. Például a Föld Nap körüli mozgásának sebessége 30 km/sec, azaz négy nagyságrenddel kisebb, mint a fény sebessége. Emiatt ez a Doppler-hatás nagyságrenddel haladja meg a fénysebesség változása miatti vöröseltolódást.

A változó sebességű fény útja

Ha a fénysebesség változik, akkor nagyobb utat tesz meg a fény, mint amit a jelenlegi fénysebesség alapján számolhatunk. Integrálva a fényutat:

Ha T = 1,5T₀, akkor a fény több mint háromszor nagyobb utat tesz, mintha állandó lenne a sebessége. A Tejúton belül, ahol T/T₀ nagyon kicsi, a fenti összefüggés elvezet a fénysebesség állandóságának jól ismert törvényéhez, mert ebben a közelítésben a megtett út: s = c₀T.

Hová kerül a fény elvesztett energiája?

A fénysebesség csökkenése azt jelenti, hogy a milliárd évekkel korábban kibocsátott foton energiája lassan csökkenni fog. Ez abból következik, hogy mai Univerzumunkban a kisebb c₀ sebesség határozza meg a                 ν = c₀/λ frekvenciát és a hozzá tartozó E = hν energiát. De hová kerül az elvesztett sugárzási energia? Ez feltölti a teret és megjelenik a sötét energia formájában! A sötét energia tehát az Univerzum múltjának hozadéka és forrása annak az erőnek, amely biztosítja az Univerzum egyensúlyát. Einstein eredetileg stacionárius világképben gondolkozott, ezért gravitációs egyenletébe felvett egy antigravitációs tagot, amellyel ellensúlyozta a gravitációs erőt és az Univerzum összeroppanását. Később Einstein a táguló Univerzum koncepciója miatt ezt a feltevést élete legnagyobb tévedésének nevezte, de aztán a gyorsulva tágulás elve miatt az antigravitációs tag mégis elfogadásra került az ősrobbanás elméletében. A fénysebesség csökkenésének koncepciója ennél tovább megy, mert kézenfekvő magyarázattal szolgál a sötét energia eredetére. Ebben a modellben az Univerzum stabilitását az biztosítja, hogy a sugárzás révén a korábbi Univerzum feltölti energiával a későbbi világot éppen annyival, amennyi szükséges a változatlan szerkezet fenntartásához.

Mikrohullámú háttérsugárzás

De hogyan értelmezhetjük a mikrohullámú háttérsugárzást? Ha az Univerzum kiterjedése véges a térben, akkor annak határánál sokkal nagyobb a fénysebesség, amiért az onnan érkező fény frekvenciája oly mértékben csökken, hogy az atomok által kisugárzott energiát leviszi egészen a mikrohullámú tartományba.

És mikor jött létre az Univerzum? Erre a kérdésre az ősrobbanás elmélete határozott választ kíván adni, amikor 13,7 milliárd évről beszél. De hogyan jöhet létre a semmiből az anyag? Ha nincs Univerzum, akkor mivel skálázhatjuk az időt és a teret? Ebben az állapotban nincs értelme az idő fogalmának. A fénysebesség csökkenésének koncepciója elkerüli ezt a logikai csapdát, hiszen nem ragaszkodik a kezdetekhez, a T/T₀ érték tetszőlegesen nagy lehet.

Mérhető-e a fény lassulása?

Tekintsünk most a jövő irányába! Ha a múltban gyorsabban haladt a fény, akkor a jövőben lassulni fog. Mennyire? Ezt is megmondja az exponenciális szabály. Például száz év múlva 100/10¹⁰ = 10^-8 mértékében lesz kisebb. A c₀ = 299 792 458 m/s fénysebesség mérési pontossága 4·10^-9, ezért esély van rá, hogy a jövőben kísérleti adathoz jussunk a fénysebesség változásának üteméről.

Melyik világmodell a helyes?

A csillagos ég a távoli múlt üzenetét hozza el hozzánk, ennek eszköze a vöröseltolódás. Ezt értelmezhetjük különböző módon, akár az Univerzum tágulásával és az ősrobbanás koncepciójával, akár a fénysebesség változásával. Azt már az olvasóra bízom, hogy ki-ki maga döntse el, melyik elképzelést tartja elfogadhatónak.

A blog további írásainak összefoglalása a linkekkel együtt megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben.

Verne Gyula óta sokaknak elindította képzeletét egy utazás a Föld belsejébe. Természetesen ott olyan magas a hőmérséklet és hatalmas a nyomás, hogy oda csak képzeletünk szárnyán juthatunk el és még egy szonda odajuttatása is jelenleg megoldhatatlan nehézséget jelent. Nézzük meg, hogy a fizika törvényei alapján mit várhatunk ettől a különös világtól. Erről készített kitűnő filmet a National Geografic is.

 Az Index „Ma is tanultam valamit” rovata is foglalkozott a témával, az idő különböző sebességű változását vetette össze a Föld közepén és felszínén. Ez jól szemlélteti Einstein általános relativitáselméletét, amely szerint még a Föld kora is megváltozik, ha eltérő gravitációs erőtérben vagyunk. A cikk azonban egy téves hiedelmet vett alapul, amikor azt állította, hogy a Föld középpontjában nagyobb a gravitáció, mint a felszínén. Ennek ugyanis pont a fordítottja igaz. A szerkesztő érdemére legyen mondva, hogy amikor a tévedést egy levélben tudomására hoztam azonnal javított a szövegen, hogy ne vezesse félre olvasóit. A félreértést alighanem az okozta, hogy a köztudat nem tesz különbséget a gravitációs erő és a gravitációs potenciál illetve nyomás között. Ennek szemléletes bemutatása is bejegyzésem egyik célja.

Gravitációs erő és földmodellek

Nézzük először a Föld legfontosabb adatait, az átlagos sugár R = 6371 km, a tömege M = 5,9724 x10²⁴ kg, amiből már következik, hogy átlagos sűrűsége 5,514 g/cm³. Határozzuk meg ebből a felszíni gravitációt, azt feltételezve, hogy a teljes tömeg a Föld középpontjában van. Ekkor a Newton-törvény szerint az m tömeg súlya:

Ahol γ = 6,673x10^-11 m³kg·s². Ebből számolva gravitációs állandó g = γM/R² = 9,81 m/s². Első pillanatra meglepő, hogy ez az érték milyen jól egyezik a tapasztalattal, hiszen önkényesen helyeztük el a Föld teljes tömegét a középpontban. Képzeljük most azt, hogy a Föld sűrűsége mindenütt azonos. Ekkor úgy számíthatjuk ki a gravitációs állandót, hogy a földgolyót egyenlő térfogatú elemek összegére bontjuk fel, külön-külön kiszámítjuk az egyes elemek gravitációs járulékát, majd ez egészet összegezzük az integrálszámítás szabálya alapján. Az eredmény ugyanaz lesz, mint amit a középpontba helyezett tömeg esetén kaptunk. Ennek oka, hogy a közelebbi pontok erősebb hatását éppen kiegyenlíti, hogy a távoli pontokból származó járulék az átlagnál kisebb.  Ez a szabály azonban csak a gömb felszínén érvényes, ha a Föld belseje felé haladunk, akkor a gravitációs állandó a mélységgel arányosan csökken a homogénsűrűségű modellben, a centrumban nulla lesz (ez a súlytalansági állapot!), míg a túloldalon megfordul. Ezt hasonlítja össze a 1. ábra a középpontba helyezett tömeg esetével:

1. ábra. A homogén sűrűségű gömb gravitációs állandójának változása (zöld szaggatott vonal és nyilak) összevetése a középpontban elhelyezett tömeg (piros vonal és nyilak) esetével. A felszínen azonos az erő a két modellben, de befelé haladva a homogén eloszlás esetén lineárisan csökken a gravitációs erő, szemben a középpontba helyezett tömeggel, ahol gyorsan növekszik.

A gravitációs erő mélységfüggését befolyásolja a sűrűség változása, amely a középpontban nagyobb (ez körülbelül duplája (13 g/cm³), mint az átlagérték, míg a felszín közelében a sűrűség az átlagérték fele (2,7 g/cm³). Ennek hatását mutatja a 2. ábra. A legújabb földmodellek összetettebb rétegeloszlást tételeznek fel, amely szerint a belső magon kívül alig változik a gravitációs erő (akár még kissé növekedhet is), majd hirtelen csökken a Föld centruma felé haladva.

2. ábra. A Föld belsejében a gravitációs erő változása különböző modellekben, zöld: homogén sűrűség, piros: lineárisan növekvő sűrűség, fekete: a jelenleg elfogadott összetett sűrűség eloszlási modell

Gravitációs nyomás és potenciális energia

A gravitációs erő mélységfüggésének nem önmagában van jelentősége, hanem azért fontos, mert ez határozza meg a gravitációs nyomást és a potenciális energia változását a Föld belsejében. Ez a két mennyiség az erővel ellentétben nem függ az iránytól, tehát skaláris mennyiség. A potenciális energiához a fizika munkafogalmán keresztül juthatunk el, ez fejezi ki az erő irányában való elmozdulás és az erő szorzatát. Ez tehát az erő integrálja a felszíntől lefelé haladva. A homogén sűrűségű gömbben a lineáris változás integrálja egy parabolához vezet, melynek minimumhelye a Föld középpontjában van. Ennek alapvető a szerepe a különböző sűrűségű gömbhéjak kialakulásában. A Föld kialakulásakor 4 és fél milliárd évvel ezelőtt még nem volt szilárd kérge, ekkor viszkózus folyadék (olvadék) volt a halmazállapota. Ebben a legkisebb energiájú helyre süllyedtek le a Föld összetételének nagyobb fajsúlyú komponensei és felülre kerültek a könnyebbek. Ez ugyan megváltoztatja a gravitációs erő mélységfüggését, de a potenciálgörbe tekintetében a minimumhely továbbra is a Föld közepe marad. A Föld anyagát különböző fémszilikátok alkotják, de a fém mennyisége, különösen a vas és a nikkel, túl sok volt ahhoz, hogy a szilikátok lekössék. Emiatt vált szét a könnyebb szilikát réteg a vas-nikkel ötvözettől. Ebben fontos szerepe volt a Föld belső hőmennyiségének, amelynek elvesztését lefékezte egy idő után a külső kéreg kialakulása. A Föld belső hőmérsékletének fenntartásában komoly szerepet kaptak a radioaktív folyamatok, amelyek a bomlás során jelentős mennyiségű hőenergiát hoznak létre. A mai Földben az urán (²³⁶U), a tórium  (²²⁹Th) és a kálium  (⁴⁰K) hosszú élettartamú izotópjai játsszák a döntő szerepet a hőtermelésben, amely jól kiegyenlíti a Föld természetes hő veszteségét. A Föld legbelső magjának hőmérsékletét 6000 fokra becsülik.

A másik fontos szereplő a gravitációs nyomás. Folyadékokban a nyomás minden irányban egyenletesen terjed, emiatt az erővel szemben a nyomás nem irányfüggő mennyiség. Ennek értékét szemléletesen úgy képzelhetjük el, hogy a felette lévő folyadék oszlop teljes súlya határozza meg. Víz esetén 10 méter magas vízoszlop súlya hoz létre akkora nyomást, mint a Föld felszínén a levegő, amit hagyományosan 1 atmoszférának nevezünk. Emiatt az óceánok legmélyén a nyomás már eléri az ezer atmoszférát is.  Mivel a Föld sűrűsége a vízének jó ötszöröse, ezért a nyomás még gyorsabban növekszik a mélység függvényében. Ha folyadéknak tekintjük a Föld fizikai fázisát, akkor ez ugyanolyan mértékben növekszik, ahogyan a potenciális energia csökken. Ezt illusztrálja a 3. ábra. A Föld középpontjában ez a nyomás már meghaladhatja az egymillió atmoszférát is.

3. ábra. A gravitációs potenciális energia (piros) és a nyomás (kék) változása a mélység függvényében

A Föld belső szerkezete és a rengéshullámok

A Föld belső szerkezetéről szerzett ismereteink fokozatosan gyarapszanak, ma már a korábbi kéreg-köpeny-mag felosztás helyett több réteget lehet elkülöníteni. Ismereteink legfőbb forrása a földrengések vizsgálata. Amikor a földrengés valahol kipattan, akkor kétféle rezgéshullám szalad végig a Földön. Az egyik a tranzverzális, vagy nyírási hullám, amikor a rezgés amplitúdója merőleges a haladásra, a másik a longitudinális, amely avval párhuzamos. Tranzverzális hullám csak szilárd halmazállapotba jön létre, mert ott nyíró erő is fellép, míg folyadékban csak longitudinális hullámok keletkeznek. Az utóbbi ezért áthatol a Föld belső folyékony övezetein is. Ez ráadásul gyorsabban terjed, mint a tranzverzális hullám. A Föld különböző pontjain elhelyezett szeizmográfok rendkívül érzékenyen észlelik a különböző rezgéshullámokat. Amikor a lökéshullám valamilyen határréteghez ér a Föld belsejében hasonlóan viselkedik, mint az üveglapra, vagy prizma felületére eső fény: részben onnan visszaverődik, részben megtörik. Ezt lehet analizálni a különböző szeizmográfok által detektált rezgések összevetésével és megállapítani, hogy milyen rétegek léteznek a Föld belsejében. A köpenyben például három réteget lehet megkülönböztetni. A legfelső szilárd és tulajdonságai sokban emlékeztetnek a kéregre, ezért a kettőt együtt nevezik litoszfrérának. Van azonban közöttük egy keskeny elválasztó vonal, a Mohorovičic diszkontinuitás (diszkontinuitásnak nevezik, amikor két réteg határvonalán valamilyen fizikai paraméter –  például a sűrűség, vagy viszkozitás – ugrásszerűen megváltozik).  Jelen esetben a szilikátkristályok összetétele tér el, amíg a kéregben a Na, K és Al jelenléte dominál, alatta már főleg az Fe és Mg fordul elő. A litoszféra alkotja a kontinentális táblákat is, amelyek az alattuk lévő folyadékszerű középső köpeny fölött úsznak. Ez a kontinensvándorlás, melynek hajtóerejét a köpenyben fellépő konvenciós áramlások biztosítják.

A köpenynek van egy alsó rétege is, amelyik viszont már szilárd. Itt már a Föld sugarának felénél tartunk, ami alatt helyezkedik el a két részből álló mag. Ezt a magot a nagy sűrűségű fémes vas és nikkel alkotja. A mag külső része viszont nem szilárd, hanem meglepően kis viszkozitású folyadék, befelé haladva a nagyobb mélységek felé nő a viszkozitás, amíg eljutunk egy újabb szilárd övezethez. Ez már a belső mag, amelynek sugara a Földének ötödét teszi ki. Nincs egyértelmű álláspont, hogy kristályos-e, vagy csak a mozgások állnak e le teljesen.

Reológia és viszkozitás

De mi lehet az oka, hogy több különböző héj alakul ki a Föld belsejében? Erre a választ a reológia adja meg, amely azt vizsgálja, hogyan változik az anyagok viszkozitása a hőmérséklet és a nyomás függvényében. A nyomás a folyadékokban egyenletesen terjed, de ennek sebessége a viszkozitástól függ. Magas hőmérsékleten kisebb a viszkozitás, de rendkívül nagy nyomás ezt a tendenciát megfordíthatja. A Föld belsejében a nyomás elérheti az egymillió atmoszférát is, ami teljesen leállíthatja a nyomás továbbterjedését. Ekkor már szilárd anyagról beszélhetünk. Ez megy végbe a Föld belsejében is. A 4. ábra szemlélteti a helyzetet. A kritikus nyomás elérésekor a létrejövő szilárd réteg úgy viselkedik, mint egy tartó boltozat, amely már nem továbbítja lefelé a nyomást, mintegy a „hátán hordja” a felette lévő rétegek súlyát. Emiatt alatta hirtelen lecsökken a nyomás, és létrejön egy alacsony viszkozitású réteg. Persze ennek súlya lefelé haladva összegződik, amíg a nyomás ismét eléri a kritikus értéket.

4. ábra. Folyékony és szilárd rétegek kialakulása a Föld belsejében. A zöld vonal mutatja a nyomás növekedését, ami elérve a kritikus értéket (piros vonal) létrehozza a szilárd fázist (kék gyűrű)

Földmágnesesség létrejötte a magban

A két folyékony héjnak jelentősen eltér a szerepe a földi folyamatokban. A külsőről már megállapítottuk, hogy felelős a kontinensvándorlásokért. A belsőben is fellépnek konvekciós áramlások, amelyek a földi mágnesesség forrását alkotják. A belső mag fémes vezetőként viselkedik, és a földi forgás kombinálódik a mag folyékony részének konvekciós áramlásaival (Coriolis erőhatás), ami köráramokat és ezáltal mágneses mezőt indukál. Ennek erősségét 25 Gaussra becsülik, amiből annak 50-ed része jut ki a felszínre. Ez alkotja azt a mágneses mezőt, ami a Napból érkező ionizáló sugárzást eltéríti, és nem engedi meg, hogy a Föld felszínére jusson. A belső mag mozgása nem követi teljesen a Föld forgását, ebből fakad, hogy a mágneses sarkok pozíciója nem esik egybe az Északi és a Déli sarkkal.  A számítások szerint a mag valamivel gyorsabban forog, mint a Föld maga (kb 1000 év alatt tesz meg eggyel több fordulatot). Feltételezik, hogy a dinamó hatás is szerepet játszik a geomágnesesség kialakulásában azáltal, hogy a köráramok mágneses tere rendezi az áramlatokat és így tovább erősíti önmagát. A tengeri talapzat egyes rétegei megőrizték, hogy a különböző földtörténeti korszakokban milyen volt a mágneses tér észak-déli polaritása. Innen lehet tudni, hogy hozzávetőleg 200 ezer évente a mágnesesség polaritást vált. Az utolsó ilyen váltás 600 ezer évvel ezelőtt következett be. A National Geografic filmjében fel is teszik a kérdést, hogy mikor fog bekövetkezni a következő átfordulás. Ha ez létrejön sokáig nélkülöznünk kel a földi mágnesesség védő hatását.

A blog további írásainak összefoglalása a megfelelő linkekkel a „Paradigmaváltás a fizikában” című bejegyzésben olvasható.

 Amikor egy tudományágban bizonyos törvények általánosan elfogadottá válnak rendkívül nehéz olyan eredményt elfogadtatni, amely azt részben, vagy egészben cáfolná. Sokkal könnyebb olyan közleményeket elhelyezni a szakirodalomban, amely nem ad igazán újat, hanem a jól bevált és elfogadott nyomon halad, csak azért legyen valami új is benne, akár a vizsgált anyag, akár a módszertan tekintetében. Ennek felel meg saját publikációm többsége is, melyeket részben a legnagyobb tekintélyű fizikai és kémiai folyóiratokban sikerült közölni. Most azonban belefutottam én is a fönt említett korlátba, amikor olyan eredményre jutottam, amely már sérthetett bizonyos tekintélyeket.

Van-e tömege a neutrínóknak?

Miről is volt szó? A részecskefizikának van két erősen vitatható állítása, amit a fizika irányadó kutatói mégis elfogadnak. Az egyik, hogy van-e a neutrínónak nyugalmi tömege. Az első megfigyelések szerint a neutrínó fénysebességgel halad, ezért a részecskék tulajdonságait összegző Standard Modell szerint nincs is nyugalmi tömege. A későbbi vizsgálatok azonban világossá tették, hogy a neutrínónak három különböző típusa van, amit elektron, müon  és tau neutrínónak neveznek. Ezek a részecskék minden tulajdonságban egyeznek, a spinjük ½, töltésük nulla, így csak abban térhetnek el, ha mégiscsak van tömegük. Ezt a különbséget az bizonyítja, hogy ezek a részecskék a képződésük után átalakulnak egymásba, amit neutrínó oszcillációnak neveznek. Erről már több alkalommal is írtam a blogban, legutóbb „A neutrínó kalandos története” című írásban. Végül is hogyan lehet eldönteni, hogy van, vagy nincs tömege a neutrínónak? Ebben segít a pontos sebességmérés, mert ha létezik nyugalmi tömeg, akkor a relativitáselmélet tömegnövekedési törvénye szerint a részecske sebessége nem érheti el a c értéket, azaz a fény sebességét vákuumban. Több mérést is végeztek különböző laboratóriumban, de a mérési határon belül mindig azt kapták, hogy a sebesség megegyezik c-vel. Sőt egyszer még az a hír is lábra kapott, hogy c-nél nagyobb a sebesség, de aztán ezt visszavonták, mert a mérés során technikai hibát követtek el. Tehát jelenleg ott tartunk, hogy az eddigi sebességmérések szerint a neutrínó nullatömegű részecske. Van azonban egy kibúvó, hiszen minden mérésnek van hibahatára, ezért nem cáfolható meg, hogy ezen belül mégiscsak kicsit lassabb lenne a neutrínó sebessége c-nél, amiből pedig megbecsülhetjük a tömeg lehetséges felső határát. A mérések fokozódó pontossága mellett most ott tartunk, hogy a neutrínó tömege, legalább is az elektron típusúé, nem lehet nagyobb, mint a parányi elektron tömegének milliomod része. Valljuk be, ez bizony elég gyöngécske magyarázat, de ha a jövőben még pontosabb sebességmérést végeznek, akkor is megmarad a kibúvó, hiszen a mérés akkor sem lesz végtelenül pontos. Nem lenne hát célszerű megnézni, hogy nincs-e olyan elmélet, amelyik magyarázná a neutrínó oszcillációt akkor is, ha a nyugalmi tömeg nulla? Már tettem is egy ilyen javaslatot, amely a „Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók” írásban olvasható.

Miért nem lehet megfigyelni a kvarkokat?

Mielőtt erre rátérnék, nézzük a másik széles körben elfogadott, de mégis vitatható hipotézist. Ez a kvarkokra, a törttöltésű elemi részecskékre vonatkozik. Addig, amíg csak az atomot felépítő elektront, protont és neutront ismertük tisztának látszott a kép. Bonyolódott a helyzet a pozitron felfedezésével, de ennek még örültünk, mert magyarázatot adott Dirac nagyszerű felfedezésének egy vitatott kérdésére, amikor megalkotta relativisztikus hullámegyenletét, amely negatív energiájú megoldásokra is vezetett. Ez lett az alapja a lyukelméletnek, amely ugyan később nem állta meg a helyét, de most nem evvel akarunk foglalkozni. Az pozitron felfedezésével csaknem egy időben került sor az első neutrínó kimutatására. Ezekre akkortájt még Nobel-díjakat is adtak. De aztán egyre-másra találtak új és újabb elemi részecskét, amire nem volt magyarázat. Ezeket két nagy csoportba lehetett osztani a spinük szerint, a félegész spinüek a barionok, az egész spinűek a mezonok. Ezek száma ma már jóval száz fölött van. De megszületett a nagyszerű elmélet, amikor két alap kvarkkal , a +2/3e töltésű up és -1/3e töltésű down kvarkból és ezek magasabb generációival és antirészecske párjukkal valamennyi bariont és mezont fel lehetett építeni. Lásd például a „Kvark színe” című írást a blogban. Bár meghökkentő volt a feltevés, hogy létezhetnek törttöltésű elemi objektumok is, de olyan jól lehetett evvel valamennyi most már összetettnek tekinthető részecskét értelmezni, ami eloszlatta a kételyeket. Ezután már természetes volt, hogy az elmélet alkotói megérdemelten nyerték el a Nobel-díjat. De itt is van egy bökkenő: ilyen törttöltésű részecskét sehogyan sem lehetett megfigyelni (lásd: „Miért nem lehet szabad kvarkokat megfigyelni". Ez fel is vetette a kérdést, vajon csak egy kitűnő rendezési elvről van szó, vagy tényleg léteznek a kvarkok, mint valódi részecskék, csak a jelenlegi kísérleti körülmények között nem tudjuk detektálni ezeket. Jött is egy magyarázat, amit „bezártsági elvnek” (confinement) neveznek, amely azt mondja ki, hogy olyan nagy erővel kapaszkodnak össze a barionokban és mezonokban a kvarkok, hogy nincs elég nagy erő, ami a kötéseket felhasítaná. Evvel az elvvel is gond van, mert a nukleonok (proton és neutron) energiáját több mint százszor meghaladó ütközési kísérletekben, ahol mindig óriási számú részecske jön létre, nem lehetett látni törttöltésű objektumokat. Hasonló a helyzet a kozmikus sugárzásban, ahol még ennél jóval nagyobb energiájú részecskék is érkeznek. Mit jelent ez? Azt, hogy a kötési energia a bezártsági elv szerint nagyságrenddel kellene meghaladja bármely megfigyelt elemi objektumét beleértve a kvarkoknak tulajdonított renormált tömeget is. Itt is felvetődik a kérdés, hogy nem kellene olyan elméleten gondolkozni, amelyik természetes módon magyarázná a kvarkok megfigyelhetetlenségét? (Lásd: „Miért nem lehet szabad kvarkokat megfigyelni?”)

Egy új elmélet születése

Az ilyen elméletek általában nem úgy születnek, hogy valaki elhatározza ennek kidolgozását, hanem ha teljesen máshonnan indul el és szinte véletlenül jut el a felismeréshez. Ez történt velem is. Érdekelt a dolog, hogy Dirac relativisztikus hullámegyenlete nem terjeszthető-e ki a többi elemi részecskére a törttöltésű kvarkokra és a töltés nélküli neutrínókra. Megpróbáltam Dirac eredeti gondolatából kiindulni, mégpedig az energia relativisztikus kovariancia kifejezéséből (ez egy négyzetes összefüggés az energia különböző összetevői között, lásd pl. „Még egyszer a Dirac egyenletről” és „A Dirac egyenlettől az általános fermion egyenletig”). Dirac zseniális ötlete volt, hogy a négyzetgyökvonást négy lineáris egyenletre bontotta fel négydimenziós mátrixok (spinorok) segítségével. Ennek a felbontásnak köszönhetjük a spin fogalmának megszületését, ami az elemi részecskék legalapvetőbb tulajdonsága, hiszen még a töltéssel és tömeggel nem rendelkező részecskék is rendelkeznek spinnel. A másik következmény az energia előjelének kétértékűsége lett. A spin és az energia két előjelének fellépése arra vezethető vissza, hogy a kovariancia formulában négyzetes kifejezések vannak, és így a pozitív és negatív értékek egyaránt kielégítik az összefüggést. Ez az összefüggés azonban egy harmadik kettősséget is rejteget, ezért számomra indokoltnak tűnt, hogy kibővítsen Dirac ötletét és a felbontást nyolcdimenziós spinorokkal végezzem el. Ez úgy volt lehetséges, ha a tömeg és töltés fogalmát általánosítom, amely ettől fogva nem egy szimpla konstans volt, hanem egy kétdimenziós mátrix, ami kifejezhető a Pauli mátrixok segítségével. Ezáltal a tömeg és töltés hasonló tulajdonságot vett fel, mint a spin. A kvantummechanikában a fizikai mennyiségeket, az energiát, impulzust és impulzusmomentumot operátorok alkotják, viszont azáltal, hogy a tömeget és töltést is mátrixok, azaz operátorok képviselik, egy olyan formalizmushoz jutunk, amelyben már minden egyes fizikai mennyiség operátor lett. Ily módon egy teljes, konzekvens kvantummechanikához lehetett jutni. Ebben a formalizmusban már közös alapra lehetett helyezni a Standard Modell összes valóban eleminek tekintett fermionját: az elektron-pozitron párt, a neutrínót és a kvarkokat is, amelyeket egyetlen új kvantumszám különböztet meg. Ebben a töltést és a tömeget a megfelelő operátorok várhatóértéke képviseli, amit az általánosított Dirac egyenlet –  amit fermion egyenletnek neveztem el –  határoz meg.

Az új egyenlet meglepő következményei

A meglepetés akkor ért, amikor az új egyenlet következményeit vizsgáltam a neutrínók és a kvarkok esetén. A neutrínóknál a tömeg és töltés várhatóértéke nulla, a relativisztikus sebességfüggés ezt a várható értéket növeli meg a tömeg esetében. De ha ez nulla, akkor nincs akadálya, hogy a neutrínó fénysebességgel haladjon. Ugyanakkor a tömeg spinor jellege avval jár, hogy a nem-diagonális elemek nem lesznek nullák és így különbséget tehetünk a háromféle neutrínó között. Tehát választ kapunk arra is, hogyan oszcillálhat egymás között a három neutrínó típus.

De mi a helyzet a kvarkokkal? A kvarkok törttöltése is mint várhatóérték adódik ki, amely azonban különbözik a töltés operátor sajátértékétől, ami csak +e és –e lehet. De mit mond ki a kvantummechanika? A mikro-objektum állapotát a hullámfüggvény határozza meg, amely bizonyos fizikai mennyiségek számára több lehetséges értéket tesz lehetővé, megadva azok valószínűségét is. A neutrínót úgy foghatjuk fel, mint a részecske olyan kvantummechanikai állapotát, ahol a két sajátérték valószínűsége megegyezik és így a várhatóérték nulla lesz. Kvarkoknál pedig azért alakul ki törttöltés, mert a +e és –e töltésállapotok súlya eltérő lesz. De ha végrehajtjuk a mérést, akkor csupán a sajátértékek egyike valósulhat meg. Ezt hívja a szakirodalom a hullámfüggvény redukciójának. Ez azt jelenti, hogy a részecskék detektálása során kizárólag olyan részecskét láthatunk, ahol vagy –e, vagy +e a töltés. Más szóval a törttöltésű kvark egy mérés előtti kvantummechanikai állapot, és nem ténylegesen detektálható részecske. Ily módon a kvantummechanika alapelve világos választ ad arra, hogy a kvarkok miért nem figyelhetők meg.

Kísérlet az eredmények publikálására

 Ha viszont két ilyen alapvető és sokszorosan alátámasztott kísérleti tényre jó választ ad az elmélet, akkor joggal bízhatunk az elmélet helyességében. Ez a részecskefizika szempontjából rendkívül fontos eredmény. Ilyenkor a kutatóban felébred a kétely: lehet, hogy valahol hibádzik az elgondolása, hiba lehet a logikában, vagy a matematikai eljárásban? Ennek legjobb próbája, ha a tudományterület legjobb kutatói ellenőrzik az elmélet és a következtetések helyességét. Erre sor kerül, mielőtt az eredmény publikálásra kerül. Ez a vizsgálat különösen szigorú a legjelentősebb folyóiratoknál. Erre a célra a fizika legtekintélyesebb folyóiratát (Physical Review Letters, PRL) választottam, már csak azért is, mert ebben a folyóiratban is jelentek meg korábban közleményeim. A benyújtás után először a szerkesztőség foglal állást, hogy érdemesnek tartja-e a munkát publikálásra, és ha igen, akkor kiküldi szakmai bírálatra. Az én publikációm nem jutott el erre a második fázisra, de nem azért, mert szakmai hibát találtak volna benne, hanem mert az eredményeket nem tartották elég jelentősnek ahhoz, hogy a PRL közölje. Arra hivatkoztak, hogy az újabban tovább emelt fontossági kritériumoknak nem felel meg az írás, szakmailag viszont nem kritizálták, sőt javasolták, hogy küldjem el a kéziratot egy erre specializált folyóiratnak. Én az elutasítást nem fogadtam el, mert az eredmények alapvető fontosságúnak tartom a részecskefizika továbbfejlődése érdekében. Ezt megírtam a szerkesztőnek, aki tett egy korrekt javaslatot  – érdemes ezért a nevét is megemlíteni: Dr. Stojan Rebic – aki javasolta, nyújtsak be fellebbezést a „Divisional Associate Editor” (DAE) testületéhez. A fellebbezést be is nyújtottam, amelyben rámutattam, hogy tévedés történt az előzetes elbírálás során, mert az eredmények jelentősége egyértelműen bizonyítja, hogy a kéziratnak a PRL-nél van a helye. Kértem ezért, hogy küldjék ki a kéziratot szakmai bírálatra. Hosszú ideig nem jött válasz, majd kétszeri sürgetés után csaknem két hónap elteltével jött az újabb elutasítás. De ismét szó sem volt szakmai kifogásról, ezúttal nem tértek ki arra sem, hogy ne lenne igazán fontos az eredmény.  Mit is írt a bírálatot elkészítő DAE szerkesztő?  Indulásként megjegyezte, hogy ő miben hisz: egyrészt abban, hogy a neutrínók lassabban mozognak mint a fény, másrészt abban, hogy a kvarkok bezártságát az erős kölcsönhatás okozza. Más szóval azt fejtette ki, hogy ő a mai elfogadott részecskefizikai koncepciókban hisz. A következő mondatban viszont elismerte, hogy nem tudja megítélni a beküldött kézirat szakmai helyességét és javasolja a kézirat speciális folyóirathoz küldését. Ez a vélemény annyira meghökkentő egy tekintélyes szerkesztőség tekintélyes tagjától, hogy érdemes az eredeti angol szöveget itt változtatás nélkül leírni:

The author proposes a generalization of the Dirac equation that leads to the possibility of neutrinos traveling at the speed of light and explains quark confinement. I believe the neutrinos don't travel at the speed of light due to their non-zero mass and quark confinement has to do with properties of the strong interaction. Since my confusion may be due to some technicality that I don't understand properly I would suggest the author to send his work to a more specialized journal, where his work could be better appreciated.

1. E.M. Wagner

Divisional Associate Editor

Physical Review Letters

A közlés elutasításának oka

Az alsóbb szintű szerkesztőség erre a véleményre alapozva utasította el végül a kéziratot. Tehát fontosabb, hogy mit hisz az önmagát inkompetensnek nevező bíráló, mint bármely tudományos szakmai érv?   Néhány századdal a Galilei-per után is kísért még az inkvizíció szelleme?

Az elutasítás valódi okát csak sejthetem. A nagy tekintélyű tudósok véleményével szemben hogyan jelentethetnének meg egy közleményt, amely avval szembemegy? Itt tart hát a fizikai véleményalkotás szabadsága napjainkban!

A blog további írásai a megfelelő linkekkel megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben.

Áthidalható-e a szakadék a józanész és a modern fizika között?

A XX. század második felének talán legjelentősebb fizikusa, Richard Feynman írta nevezetes könyvében (QED. The strange theory of light and matter), hogy az elektromágnesesség közvetítője, a foton olyan tulajdonságokkal rendelkezik, amelynek megértése a klasszikus fizika alapján nem lehetséges. Itt olyan tulajdonságokra kell gondolni, hogy a foton mozgása során úgy „tapogatja” le a pályáját, hogy kipróbál minden utat és egyes lépesekben gyorsabb, mint a fénysebesség, sőt időben visszafelé is haladhat, bizonyos átalakulások – például a párképződés –  előbb fejti ki hatását, mint amikor létrejön. Ez nemcsak a relativitáselméletnek mond ellent, hanem a józanésznek is. Írjuk hát le a józanészt és elégedjünk meg annyival, hogy matematikai formuláink jól írják le megfigyeléseinket és ne próbáljunk meg hidat teremteni a józanész és a mikrovilág jelenségei között? Jelenleg ez az általános felfogás a fizikában, de vizsgáljuk meg annak okát, hogy miért viselkedik ilyen különlegesen a fény, amikor kölcsönhatásba kerül az anyaggal.

Mindennapi fogalmaink eredete

Honnan származnak fogalmaink a mindennapokban térről, időről és mozgásról? Legfőbb információforrásunk a fény. Minden időpillanatban óriási számban érkeznek szemünkbe a fotonok, ahol az irányuktól és színüktől függően más-más ponton hoznak létre elektronokat a retinán, melyek külön idegpályákon jutnak el az agyba, amely feldogozza a rengeteg információt összehasonlítva a különböző irányokat, távolságokat, megkülönböztetve a színeket és intenzitásokat alakítja ki azt a képet, amit látunk. Ennek ideje bámulatosan rövid, alig egy tizedmásodperc. Tér és időképzetünk alapja az összehasonlítás, összevetjük, hogy mi van közel és távol, melyik tárgy kicsi és melyik nagy, elrendezzük a tárgyakat irányok szerint, az eseményeket is sorba rakjuk: mi volt előbb és mi volt utóbb.

A józanész paradigmaváltása

A józanész fogalomrendszere is változik, ebben nagy szerepe van, hogy műszereinkkel kitágítjuk látóhatárunkat.  Hosszú ideig gondoltuk úgy, hogy a Föld lapos és körülötte keringenek a Nap, a Hold és a csillagok. Később felismertük, hogy a Föld véges és körül hajózható, távcsöveink megmutatták, hogy milyen óriási az Univerzum a Földhöz képest, emiatt gondolkozásunknak is váltani kellett, bekövetkezett a kopernikuszi fordulat, és ma már a józanész számára természetes, hogy a Földet nem a világ közepének, hanem a Nap körül keringő bolygónak tekintjük.  A műszerek fejlődése tette lehetővé, hogy megismerjük az elektromágnesesség törvényeit. A műszerek a XX. század előtt nem jutottak el addig a határig, hogy láthatóvá tegyék az atomok és molekulák világát, ezért a folytonosság fogalma gyökeresedett meg tudatunkban. Erre alapozta a matematika is a differenciálás és integrálás szabályait, és ez jelent meg a fizika egyenleteiben, legyen szó akár a mechanikáról, a termodinamikáról, vagy az elektromágnesesség alapegyenleteiről. A folytonosság jegyében képzeltük el a bolygók mozgásait is. Ha ugyan a józanészhez nem is jutottak el feltétlenül a fizika egyes törvényei, de konfliktus nem alakult ki a fizikai megismerés és a józanész között. A fizikusok is ugyanazt a tér és idő fogalmat használták, ami a mindennapok gondolkozásával megegyezett.

A józanész konfliktusa a modern fizikával

Meglepetést ugyan okozott, de nem okozott törést a gondolkozásban az atom fogalmának kialakulása, sőt még a fény legkisebb egységének a fotonnak feltételezése sem, mert ettől még nem csorbult a mozgás folytonosságának koncepciója. Az igazi törést Bohr atommodellje okozta, aki a pozitív atommag körül a negatív töltésű elektronok mozgását a bolygómozgáshoz hasonlította, ahol a vonzó erőt nem a gravitáció, hanem az elektromos vonzás biztosítja. A meghökkentő az volt, hogy a körpályán keringő elektronnak folytonosan sugározni kellene az elektromágnesesség törvényei szerint. Ehelyett csak ugrásokra kerül sor az elektronpályák között, amelyek diszkrét vonalakat hoznak létre a fény spektrumában. Ezek az ugrások a fény kvantumának, a fotonnak létrehozói. A józanésszel harmóniában lévő fizikusi gondolkozásban az jelentett törést, hogy az energia változása a pályák között ugrásszerűen és nem folytonosan megy végbe. Az egyes pályákon mozgó elektronokat nem is láthatjuk, mert onnan nem lépnek ki fotonok. Olyan elmélet kellett, amelyik az ugrások alapján ad információt, hogy milyen állapotok között jön létre az átmenet. Más szóval a pályákról nem is tudunk közvetlenül semmit, ameddig ugrásra nem kerül sor. Emiatt az elektronpálya alapvetően eltér a klasszikus pályától, amelyben – legalábbis elvben – minden pillanatban tudjuk, hogy épp hol van a vizsgált fizikai objektum. Ezért olyan fizikai elmélet kell, amely az ugrásokból – azaz a változásból – kiindulva magyarázza a változatlan állapotot. Ez új megfogalmazást kívánt az energiára számára is. A klasszikus elméletben azt mondtuk az energiáról, hogy a mozgás során megmarad, de az új elméletben megfordul a logika: úgy definiáljuk az energiát, amely az idő függvényében nem változtatja meg a részecske állapotát, azaz a pályát. Ehhez társul az impulzus fogalma, amely a hely függvényében nem hoz létre változást. Ez matematikailag azt jelenti, hogy az energiához az idő-szerinti, az impulzushoz a tér koordináták szerinti differenciálhányadost kell rendelni, amit a matematika operátornak tekint. Az új felfogás a fotonok energiáját, impulzusát és impulzusmomentumát veszi alapul, ami a ℏ Planck állandóval arányos, és emiatt a deriváltakat is evvel kell megszorozni (lásd „Út a kvantummechanika megértéséhez”.  De mi az, amit az energia nem változtat meg, amit tehát a részecskék állapotának, vagy pályájának tekintünk? Ezt nevezi a kvantummechanika állapotfüggvénynek. Ha az energia operátora nem változtatja meg a pályát, akkor az állapotfüggvény alakja az idő-szerinti deriváláskor nem változik meg csak szorzódik egy konstans mennyiséggel. Ez a konstans lesz, amely megadja az energia mért értékét a vizsgált mikro-állapotban.

Pálya időfüggés nélkül

Nagyon különös ez a pálya, amit a kvantummechanika stacionárius állapotnak nevez, mert nincs benne időfüggés. Beszélhetünk-e egyáltalán mozgásról az atomban kötött elektronoknál? A klasszikus értelemben nem, mert nem a mikor és hol kérdésére válaszolunk, hanem a hol és mekkora valószínűség kérdése jön elő. Az állapotfüggvény ugyanis megmondja nekünk, hogy az elektron az atomban bizonyos pozícióban mekkora valószínűséggel tartózkodik. Mondhatjuk úgy is, hogy az elektron már nem a tér és idő, hanem a tér és valószínűség dimenziójában „mozog”! Ez a felfogás már gyökeresen különbözik attól, amit a józanész fel tud fogni. Ráadásul aláássa determinizmusba vetett hitünket is. Vajon az elektron sorsát a véletlen szabja meg, vagy csak nem ismerjük azt az okot, amiért az elektron egyszer csak elhatározza magát, hogy átugrik egy másik pályára foton kibocsátás közben? Ez a kérdés végighúzódik a modern fizikában egészen napjainkig, amit EPR paradoxonnak nevez az irodalom Einstein, Podolski és Rosen felvetése nyomán. A szerzők véleménye szerint a kvantummechanika nem teljes, ki kell bővíteni egy „rejtett” paraméterrel, amely megmondja, hogy mikor ugrik az elektron az egyik állapotból a másikba, vagy konkrét értéket ad az előzetesen valószínűség eloszlással jellemzett fizikai mennyiségnek. Einstein és szerzőtársai szerint a valószínűség megjelenése a mikrovilágban csupán onnan származik, hogy előttünk ez a paraméter rejtve van.

A rejtett paraméter koncepció cáfolata

A rejtett paraméter létezését többen cáfolni próbálták, legmesszebbre Bell jutott. Ő két egyidejűleg kibocsátott elektronpár polarizációját (mágneses mezőben való két lehetséges beállását) vizsgálta és felvetette, hogy különböző mérési elrendezéseket kombinálva mekkora valószínűséget kapunk egy adott polarizációs irány bekövetkezésére, ha összehasonlítunk két elvet. (A későbbiek miatt megjegyezzük, hogy hasonló kísérleteket végezhetünk fotonokkal is.)  Az egyik elv a szokásos kvantummechanika, a másik, amikor egy rejtett paraméter határozza meg a mérés kimenetelét.  Bell számításai szerint a két koncepció eltérő eredményre vezet, amiből levonta a következtetést, hogy a rejtett paraméter nem illeszthető be a kvantummechanikába. Gondolatmenete a hagyományos „józanész” és a kvantummechanika irányfogalmának ütközését tükrözi. Abból indult ki ugyanis Bell, ha a mérés pillanatában a rejtett paraméter határozta meg a polarizációs irányt, akkor a mérés előtti állapotban – ahol még nem tudjuk, hogy milyen irányú volt a polarizáció – szintén determinálva van a polarizációs irány a rejtett paraméter által. A szokásos irányfogalomnak ez a feltevés tökéletesen megfelel. A kérdés buktatója, hogy tényleg jogos ez a feltevés? A mérés eredményeként már indokolt arról beszélni, hogy meghatároztuk a polarizációs irányt. Miért? Mert látjuk a berendezést, amelyben a mágnesek síkja kijelöli az irányt és evvel vetjük össze a vizsgált elektron polarizációját. Itt a hangsúly azon van. hogy LÁTJUK a berendezést, tehát felhasználjuk azt a hatalmas információmennyiséget, ami a berendezésből a szemünkbe jut. De van-e értelme az iránynak az elektronpár elindításakor? Ekkor még nem kerül összehasonlításra az elektron polarizációja a felhasznált berendezés által kijelölt síkkal, ekkor még csak képzeletünkben jelenik meg a vonatkoztatási irány.  Ennek alapja, hogy él bennünk egy kép, amely az irány fogalmát mindenhova kiterjeszti, és természetesnek vesszük az irány objektív létezését, hiszen bárhová nézünk, onnan rengeteg foton jut a szemünkbe. Így működik a józanész és ennek felel meg Bell induló hipotézise is!

A cáfolat cáfolata

Aspect, francia fizikus azonban elvégzett egy kísérletet, amely nem volt összeegyeztethető Bell magyarázatával. Elindított két fotont, amelynek polarizációját a forrástól két azonos távolságú, de ellentétes irányú berendezéssel határozta meg. Határozott korrelációt talált: ha az egyik foton polarizációja felfelé mutatott, akkor a másik az esetek többségében lefelé irányult. Itt tudnunk kell, hogy a megmaradási törvény miatt a két képződő foton polarizációja ellentétes. Ha most létezik egy rejtett paraméter, amelyik determinálja a polarizációs irányt, akkor természetes, hogy a két foton polarizációs iránya a méréskor is ellentétes marad. Ha viszont nincs ilyen rejtett paraméter, akkor a kvantummechanikai véletlen mondja meg, hogy a két mérés milyen eredményre vezet, tehát nem várnánk korrelációt.  Felvetődik a kérdés, hogy baj van-e a kvantummechanikával, amely pedig olyan kitűnő magyarázatot ad a mikrovilág jelenségeire, vagy Bell okoskodása téves? A jelenleg elfogadott álláspont szerint egyikről sincs szó! Ennek alapján vetették fel az összefonódott állapotok koncepcióját. Azt tételezik fel, hogy a két foton a szétválás után is kapcsolatban marad, és amikor az egyik foton polarizációja a mérés miatt „fel” állapotba kerül, akkor ez a másikat átviszi a „le” állapotba. Ezt nevezik nem lokális kölcsönhatásnak. Erre a magyarázatra alapítják a kvantum teleportálás jelenségét (lásd: „Hogyan hozhatunk létre teleportálást a kvantummechanika szerint”). A teleportálás alatt azt értik, hogyha létrehozunk egy összefonódott kvantumállapotot, akkor az egyik helyen elvégzett állapotváltozás azonnal kivált a másik helyen egy tükörfolyamatot.

A józanész konfliktusa

A fenti gondolatmenet tanulsága, hogy a józanészre alapozott irányfogalom megtartása miatt az elmélet épp a józanésszel szemben álló koncepcióhoz vezet. Nem könnyebb ennél elfogadni, hogy az irány fogalma a valódi megfigyelésekre korlátozódik és nem használható, amikor az irányt csak elképzeljük? Persze a teleportálás gondolata olyan csábító, hogy nehéz lemondani róla!

Van-e akkor szükség a rejtett paraméterre, hogy magyarázzuk Aspect kísérletét? Van is, meg nincs is. A kvantummechanika a hullámtermészet matematikája, amelyben szervesen ott van a hullám fázisának fogalma. Ez a fázis ismeretlen a mérés előtt, de kulcsszerepe van az interferencia létrejöttében és a polarizáció meghatározásában. Ezt a fázist, amely „körbejár” a két foton haladása során, nem ismerjük ugyan a képződéskor, azaz értéke rejtve marad előttünk, azt viszont tudjuk, hogy kezdetben épp ellentétes a fázis és az is marad a későbbiek során. Ez magyarázza a korrelációt. De ez a fázis nem kiegészíti a kvantummechanikát, ahogy azt az EPR paradoxon feltételezte, hanem annak természetes tartozéka.

A fény különleges természete

De térjünk vissza az eredeti kérdéshez, hogyan magyarázhatjuk a fény különleges viselkedését?  Képzeljük magunkat egy foton helyébe, amelyik létrejön az elektron ugrása során két állapot között. Mit „tudhat” ez a foton a világról, amíg nem kerül kölcsönhatásba az anyaggal? Vagy megfordítva a kérdést, mit tudhatunk mi a fotonról, amelyik éppen létrejött, de még nem került kölcsönhatásba semmivel? Összehasonlítás hiányában beszélhetünk-e arról, hogy a foton éppen merre halad? Még cifrább a helyzet, amikor a kvantumelektrodinamika által feltételezett virtuális fotonokra gondolunk. Itt a virtualitás alatt azt érti az elmélet, hogy ezek a fotonok nem figyelhetők meg általunk, de erre a feltételezésre alapozva rendkívül pontosan írhatjuk le az elektron mágneses tulajdonságait. E-nélkül még az elektron relativisztikus elmélete is csak közelítő magyarázatot tud adni az elektron energiájára mágneses mezőben.

A gömbhullám hipotézis eredete

Ha képesek vagyunk megszabadulni a mindennapok tapasztalataira alapozott térfogalomtól, akkor közelebb juthatunk a foton mozgásának megértéséhez. Huygens érdeme, hogy magyarázatot adott a fény gömbhullámokban való terjedésére. A gömbhullám úgy jön létre, hogy annak minden egyes pontja gömbhullámot indít meg. Mi ennek az oka? Mivel a foton „nem lát” irányokat, így számára minden irány egyenrangú. Ezt úgy fogjuk fel, hogy a foton minden pillanatban mindenfelé azonos valószínűséggel halad, és emiatt indul el egy újabb gömbhullám minden egyes pontból, ahova a fény már eljutott. Ezeknek a gömböknek határfelülete hozza létre azt az eredő gömböt, melynek felületén a foton kölcsönhatásba kerülhet az anyaggal. Feynman már említett könyvében szemléletesen magyarázza körbeforgó nyilak segítségével az egyes gömbhullámok összegződési szabályát. Ezek a nyilak felelnek meg a fázis változásának, de mi sohasem az egyes nyilak hatását figyeljük meg, hanem a számtalan nyíl eredője határozza meg a kölcsönhatást. Ott ahol a nyilak összegződnek kölcsönhatásba lép a fény, de azokban a pozíciókban, ahol a nyilak összege nulla, már nem hagy nyomot. Így egyeztethető össze a gömbhullámban való terjedés koncepciója a fény egyenes vonalú terjedésével, de így érthetjük meg a fényszóródás okát is. Erre példa, ha a forró nyári nap elől egy fa árnyékába állunk, miért nem lesz ott koromsötét. Ennek oka, hogy a fa mellett elhaladó gömbhullámok szórt fénye besüt a lombkorona alá is. Pedig, ha a foton apró száguldó részecske lenne, az árnyékban teljes sötétség borulna ránk.

A matematika és a fizika határterületén

Alapszabály a fizikában, hogy különbséget tegyünk az elemi objektumok két állapota között, az egyik, amely még nincs kölcsönhatásban a környezettel, a másik, amikor a kölcsönhatás létrejön. Az utóbbi eset szabályait a fizika mondja meg, az előbbit a választott matematikai modell. A ténylegesen megfigyelt hatás engedelmeskedik az oksági elvnek és nem enged meg olyan kölcsönhatást, amely gyorsabban terjed, mint a fény. A választott modell lépéseiben a matematikai szabályokat kell követni, de amikor eljutunk a tényleges kölcsönhatásig, akkor „kiesnek” a fiktív, fizikai képünkkel ellentétes elemek. Ha ezt a kettősséget megszokjuk, akkor feloldhatjuk a kvantummechanika paradoxonjait és megtalálhatjuk a hidat a józanész és a modern fizika között.

A blog további írásainak összefoglalását a linkekkel megtaláljuk a „Paradigmaváltás a fizikában” című írásban.

Az ősrobbanás elméletek máig vitatott kérdése, hogyan jöhetett létre az Univerzumban az anyag dominanciája az antianyag felett. Természetesen az is megkérdezhető, hogy bizonyított-e az anyag fölénye. Nem lehet, hogy a tőlünk távoli galaktikákban fordított a helyzet és azokban az általunk antianyagnak nevezett részecskék világa uralkodik? Ez azonban nagy valószínűséggel kizárható, mert a galaktikák helyzete egymáshoz képest is változik és sok csillagászati megfigyelés tanúskodik a galaktikák ütközéséről. Ilyen a Tejútrendszerünkkel is meg fog történni egykor, amikor a közeledő Androméda köd eléri csillagrendszerünk külső határait. Ha viszont anyag és antianyag találkozik, akkor megsemmisítik egymást és beláthatatlanul sok energia szabadul fel az ilyen ütközések során. Bár sok megfigyelés mutat galaktikák közötti ütközésre, de ezek nem játnak akkora sugárkitörésekkel, amelyek sokszorosan meghaladnák a szupernóva robbanásokét.

Honnan ered a természet aszimmetriája?

A kérdés úgy is felvethető, hogy miért létezik a természet aszimmetriája, amely a részecskék és antirészecskék kettős világában jelentkezik, hiszen minden részecskének létezik antirészecske párja, az elektron esetén ez a pozitron, a proton esetén az antiproton, és ezekben a párokban az elektromos töltés előjele éppen fordított. De szintén van antirészecske párja a töltéssel nem rendelkező neutronnak is, ezt hívjuk antineutronnal. A töltés hiánya a neutron összetett szerkezetével van kapcsolatban, amelyet három kvark hoz létre, a +2/3e töltésű up kvark töltését két -1/3e töltésű down kvark töltése kompenzálja, míg az antineutront antikvarkok építik fel, melyekben a töltések előjele épp fordított. Létezik semleges töltésű valóban eleminek tekintett részecske is, ilyen a neutrínó, ahol azonban máig vitatott, hogy meg kell-e különböztetni részecske és antirészecske típusú neutrínókat, vagy a neutrínó önmaga antirészecskéjének tekintendő-e.

Annihiláció és párképződés

Amikor a részecske találkozik antirészecske párjával, akkor az ütközéskor bekövetkezik az annihiláció gamma sugárzás kibocsátásával együtt. A folyamat megfordítható, mert a gamma sugarak, ha elég nagy az energiájuk ütközéskor részecske párokat hozhatnak létre: létrejöhet egy elektron-pozitron pár, amikor a sugárzás energiája meghaladja az 1 MeV értéket, de proton antiproton pár is, amikor ehhez elegendő a sugárzás energiája (legalább 2 GeV). Olyan folyamatot azonban nem lehetett megfigyelni, amikor a sugárzás hatására két elektron, vagy két pozitron alakult volna ki, azaz a semleges töltésű gamma sugarak nem hozhatnak létre töltéseket, ez a töltésmegmaradás elve. A pozitív és negatív töltések egyensúlya jellemzi földi viszonyainkat is, bár lokálisan a töltések elkülönülhetnek például kondenzátorokban, a felhők világában, de elektromos vezetőkben is, de összességében kialakul a töltések egyensúlya. Ez jellemzi az atomok és molekulák világát is. Kitekintve a csillagok világára, ott is a töltésegyensúly jellemző, bár a plazma állapotban nem találnak egymásra a pozitív atommagok és a negatív elektronok, mert a magas hőmérséklet szétveti az atomokat.

Töltésegyensúly a részecskevilágban

A töltésegyensúly azonban nem jelenti az anyag és antianyag egyensúlyát, mert a pozitív proton és a negatív elektronok száma egyensúlyban van a részecskevilágban, de a kérdés, hogy miért csak kivételesen és rövid ideig maradhatnak fel a szintén töltésegyensúlyt képviselő antiproton és pozitronból felépülő antiatomok? Van-e olyan fizikai folyamat, amely nem két azonos tömegű elemi részecskét hoz létre, hanem egy protont és egy elektront? Ha létezne ilyen folyamat, akkor a statisztikai szemléletünk már kulcsot adhatna ahhoz, hogyan került az anyag fölénybe az antianyag felett. Persze ilyenkor is egyenlő eséllyel jöhetne létre egy anyagnak tekintett proton-elektron pár, mint az antiproton és pozitron együttese, de ez csak egy statisztikai egyensúlyt jelentene, mert a véletlen különbség a kétféle pár mennyisége között elvezethetne egy olyan folyamatra, amikor az annihiláció eltüntetheti a kisebbségben képződő antianyagot és fennmaradna a véletlenül előálló többlet, amit ma anyagnak nevezünk. Ezt tekintik az ősrobbanás elméletben a részecske „kannibalizmusnak”, aminek lezajlása után maradna fent az anyagból felépített univerzum. Az elgondolás gyenge pontja, hogy mindmáig nem figyelhető meg olyan folyamat, amikor a gamma sugarak proton-elektron párt hoznának létre. Kibúvóként persze felvethető, hogy az ősrobbanás korai korszakában a hatalmas energiasűrűség miatt még voltak ilyen folyamatok, melyeket konszolidált univerzumunkban nem tudunk megfigyelni.

Létrejöhetnek-e azonos előjelű töltések a gamma-sugarakból?

A magyarázathoz azonban elindulhatunk más oldalról is. Nem lehetséges mégis olyan folyamat, amikor nem érvényes a töltésmegmaradás és létrejöhet két elektron, vagy két pozitron a gamma sugarak ütközésekor?  Ha lehet ilyen folyamat, akkor a statisztikai magyarázat elvezethet az anyag dominanciájához. A főkérdés azonban, hogy milyen szimmetria testesül meg a kétféle töltés mögött, Erre kézenfekvő magyarázat, hogy a háromdimenziós tér kiralitása, amit a jobb és a bal kéz kettősségével jellemezhetünk. Ezt az aszimmetriát megvalósíthatjuk  gamma sugarakkal is. Hogyan? A történeti hűség megköveteli, hogy megemlítsem: az ötlet eredetileg Kaslik Gyulától származik. Bocsássunk egymásra merőlegesen két gamma sugarat. Fontos azonban a két sugár polaritása is, ami a két cirkulárisan poláris komponens szétválasztása esetén megvalósítja a két lehetséges királis állapotot. Legyen például a két gamma sugár polarizációja jobbos forgásirányú. Ekkor két elrendezést lehetne összehasonlítani, ahol az egyik sugár x irányból jönne, míg a másik lehetne +y, vagy –y irányú. Az egyik esetben két elektron, a másikban két pozitron képződése várható. Kritikus természetesen, hogy a két gamma sugár mekkora hatásfokkal hozhat létre részecskéket. Erre elvi lehetőséget nyújt a kvantumelektrodinamika, mert ugyan a fotonok nem rendelkeznek töltéssel, ami az elektromágneses kölcsönhatás alapja, de virtuálisan – tehát kísérletileg nem detektálható módon – elektron-pozitron párokat hoz létre. Ennek vákuumpolarizációs hatása már elindítja a gamma-gamma kölcsönhatást, ami két részecske létrehozását eredményezi, és mivel a kísérleti elrendezés az ütközés helyén királis szimmetriával rendelkezik, így a kiralitás megmaradás törvénye magával hozza a képződő két részecske kiralitása azonos legyen, azaz vagy két részecske vagy két antirészecske jöjjön létre, amikor is a képződő elemi részecskék töltésének előjele megegyezik.

Milyen kísérlet bizonyíthatná a képződő töltések azonos előjelét?

Ez a kísérlet segíthetne a töltés eredetének tisztázásában és kulcsot adna az anyag dominanciájának megértéséhez is. A feltételek teljesítése nem könnyű, de nem is megvalósíthatatlan. Polarizált gamma sugár nagy teljesítményű szinkrotron fékezési sugárzásából nyerhető. Ehhez azonban 1MeV fölötti energiára van szükség, ilyen szinkrotron csak nagy nemzetközi laboratóriumokban áll rendelkezésre, ilyen a FERMI laboratórium, vagy az LHC. Az elektron többlet, vagy pozitron többlet kimutatása sem könnyű feladat, mert el kell kerülni a közeggel való ütközést az erős ionizáló hatás miatt, ami nagyszámú részecske keltésével zavaró háttérjelet adna. Emiatt a magas fokú vákuum a mérő kamrában alapkövetelmény. Célszerű időzített impulzusokat a detektorba belőni és az anódhoz, illetve katódhoz eljutó pozitronok illetve elektronok hatását egy jól kiegyenlített híd segítségével összevetni. A bizonyítékot az jelentené, ha a hídegyensúly felborulása a két elrendezésben fordított lenne. Ez a technika már kisszámú részecske keletkezésekor is mérhető jelet adna. A kísérlet megvalósítása fizikusok és mérnökök összehangolt munkáját igényelné. Egy ilyen mérés költsége ugyan jelentős lenne, de jóval szerényebb, mint a gravitációs hullámokat kimutató LIGO, vagy a Higgs bozon detektálására irányuló kísérleteké. Viszont a várható eredmény jelentős lökést adna, hogy tisztázni tudjuk a részecskefizika és a kozmológia  fontos kérdéseit,  és ez indokolttá teszi egy ilyen projekt megvalósítását.  

A blog további írásait összegzi a megfelelő linkekkel együtt a „Paradigmaváltás a fizikában” című bejegyzés.

A két kölcsönhatás eltérő világa

Aligha lehetne két jobban eltérő kölcsönhatást találni, mint az elektromágneses és a gyenge-kölcsönhatás. Az elektromágnesesség közvetítője a foton akár milliárd fényév távolságból is megérkezhet hozzánk egy távoli galaxisból, szemben a gyenge-kölcsönhatást közvetítő W és Z bozonokkal, melyek hatótávolsága az atommagnál is kisebb, úgy 10^–16 m nagyságába esik. Elmondható ez az élettartalmukról is, a milliárd éves foton nem ritkaság, míg a W bozon élettartama nem hosszabb 10^–24 másodpercnél. Szintén nagyon eltérnek tömegükben és töltésükben is, a fotonnak nincs nyugalmi tömege, míg a két gyenge-kölcsönhatási bozon a részecskevilág nehézsúlyú bajnoka, ha eltekintünk a Higgs bozonnak tulajdonított részecske tömegétől, akkor valamennyi egyéb megfigyelhető részecske tömegét meghaladja a W és Z bozon. Ami pedig a töltésüket illeti a fotonnak nincs, a W bozon pedig +e illetve –e elemi töltéssel rendelkezik, hasonlóan az elektronhoz és a pozitronhoz. A W⁺ és W^– egymás részecske-antirészecske párja, míg a fotonok világa nem ismeri ezt a kettősséget. Abban is nagy a különbség, hogy az elektromágnesesség kölcsönhatási erőt (vonzást vagy taszítást) hoz létre két objektum között, míg a gyenge-kölcsönhatás átalakítja az egyik részecskét a másikba.  Abban is különböznek, hogy az elektromágneses kölcsönhatás csak töltött objektumok között jön létre, viszont a gyenge-kölcsönhatás minden részecskére hat. Csupán egy dologban egyeznek: egyaránt a spin S = 1, azaz bozonokról van szó. Evvel szemben sokkal nagyobb a hasonlóság a az elektromágnesesség és a gravitáció között, nézzük akár az időtávot, vagy a kölcsönhatások távolságfüggését. Ezért hatott a fizikus társadalomban a meglepetés erejével, hogy a gyönge és elektromágneses kölcsönhatás közös alapra helyezhető, míg a gravitáció nem volt bevonható az egyesített mezőelméletbe (Sheldon Glashow. Steven Weinberg, Abdus Salam, Nobel díj: 1979).     

Az átalakulások megmaradási elvei

A gyenge és elektromágneses kölcsönhatás eltéréseinek és mélyen fekvő hasonlóságuknak megértéséhez szemléletes kulcsot ad a részecskék fénysebességű forgásmodellje (Lásd: „Az elemi részecskék mozgásformái”).  Először azt kell megértenünk, hogy milyen állapotváltozást hoz létre a két kölcsönhatás. Az elektromágnesesség hatását legkönnyebb az elektron példájával szemléltetni. Az atomban, vagy molekulában kötött elektron pályáját az impulzusmomentumukkal jellemezhetjük, melynek értéke a redukált Planck állandó többszöröse lehet : Lℏ. Az elektron állapotváltozása során az L kvantumszám eggyel változik, legyen szó a foton elnyelésről (abszorpció), vagy kibocsátásról (emisszió). Ilyenkor az elektron pályamozgásának változása hozza létre a foton S = 1 spinjét, azaz ℏ impulzusmomentumát.  Szemléletesen úgy mondhatjuk, hogy a „keringő” mozgás alakul át a foton saját forgásává. Hasonló a magyarázat a mágneses mezőben Larmor precessziót végző S = ½ spinű elektron rezonancia átmenetekor, mert a spin mező irányú komponense is egységnyit változik a foton abszorpciója, vagy emissziója során. Ekkor a mágneses mezőben polarizált elektron állapotának  megváltozása biztosít forrást  a foton impulzusmomentumához. Mindkét esetben az energiamegmaradás mellett az impulzusmomentum megmaradása vezet a kvantumátmenetek kiválasztási szabályához. Ehhez még hozzá kell tenni, hogy az átmenetek során az elektronok nyugalmi tömege nem változik meg.

Annihiláció és párképződés

Létezik egy másik kapcsolat is a fotonok és a részecskék között, az annihiláció és a párképződés. Az előbbi esetben egy-egy azonos tömegű részecske és antirészecske eltűnik gamma-sugárzás létrejöttével, a másik folyamat ennek fordítottja, amikor a foton létrehoz egy részecske-antirészecske párt, például egy elektront és egy pozitront. Ez már a nyugalmi tömeg létrejöttének és eltűnésének folyamata. A kiválasztási szabály, hogy az energia, a töltés és a spin (impulzusmomentum) megmaradjon.  Mivel a fotonnak nincs töltése, ez a szabály azt jelenti, hogy a képződő két részecske ellentétes előjelű töltéssel rendelkezik, másrészt a foton S = 1 spinje megköveteli, hogy a két új részecske egyaránt ½ spinnel rendelkezzen. A fénysebességű forgásmodellben a feltétel azáltal teljesül, hogy az elektron és pozitron kettős forgásának ellentétes a kiralitása, és így az annihiláció során kioltódik a „második” forgás az ellentétes sodrásirány miatt, miközben az „első” forgás megmarad, ami pedig nem más, mint a foton. A „második” forgás megszűnéséhez az is kell, hogy a frekvenciák megegyezzenek, azaz csak két azonos nyugalmi tömegű részecske és antirészecske semmisítheti meg egymást. Párképződéskor viszont megfordul a helyzet, ekkor a fénysebességű haladó mozgás két ellentétes perdületű forgásra hasad fel, amiért a képződő kettős forgások kiralitása, azaz töltése ellenkező előjelű lesz, a foton ℏ impulzusmomentuma pedig két egyenlő részre válik szét.

Leptonok

Térjünk át a részecskeátalakulások megmaradási szabályaira! Nézzük meg ehhez az elektron (e) és „nagy-testvérei” a müon (μ) és a tau részecske (τ) esetét! Ezek a töltött leptonok, amit „anyagnak” nevezünk, ha a töltés negatív, és „antianyagnak”, ha pozitív. Szintén a leptonok közé tartoznak a töltéssel nem rendelkező neutrínók (ν).  Ebben a „családban” a töltés és a spin azonos, viszont a nyugalmi tömeg erősen különbözik, a müon tömege 207-szer, a tau részecskéje 3477-szer nagyobb az elektronhoz viszonyítva. Honnan származnak ezek az arányok? Erre a részecskék tulajdonságait összegző Standard Modell sem adja meg a választ, ezért ezeket az értékeket fogadjuk el, mint kísérleti tapasztalatot. A két nehezebb részecske a stabil elektronnal szemben viszonylag rövid életű (müon: 2,2x10^–6 s, tau: 2,9x10^–13s) és bomlásuk egyik végterméke az elektron. A részecskék világában ez az élettartam nem számít rövidnek, mert amikor gamma-sugárzás jön létre a részecskék bomlás során 10^–20 s a tipikus felezési idő. A viszonylag lassú bomlás oka, hogy leptonoknál a gyenge-kölcsönhatás idézi elő a folyamatot, ahol az elektromágneses átmenetek tiltottak.

A gyönge-kölcsönhatási bozon spirálmozgása

Az első kérdés, ami felmerül, hogy miért nem gamma-sugárzás kibocsátásával megy végbe a bomlás, hiszen sem a spin megmaradás, sem a töltésmegmaradás szabálya nem sérülne (a töltés nem változik, a spin vetületi kvantumszám ½ és –½ közötti ugrása pedig megfelel a foton S = 1 spinjének). Az ilyen átmenet tiltását a részecskék fénysebességű forgásmodelljével értelmezhetjük. A foton egytengelyű forgás, amely a kéttengelyű forgás (tehát a fermion) egyik komponensét tudja megváltoztatni. Ahhoz, hogy mindkét forgási frekvencia megváltozzon két lépésre van szükség. Első lépésben a gyenge-kölcsönhatás szétválasztja a töltést és a tömeget két független részecske létrehozásával. Az egyik a fotonhoz hasonlóan bozon (S = 1) a másik fermion (S = ½), ez megfelel az impulzusmomentum megmaradási szabálynak. Az így képződő W bozon azonban jelentősen különbözik a fotontól, mert átveszi a müon töltését és van jelentős tömege is. Egytengelyű forgásnak úgy lehet töltése, ha a fénysebességű terjedési irány merőleges a forgástengelyre, mert ekkor fellép a Coriolis-erő, ami a töltés eredete („Az elemi részecskék mozgásformái”). Ez a mozgás egy spirálist hoz létre a forgási sugár növekedése miatt, amit az r = r₀ + ct összefüggés ír le. Itt r₀ = h/m₀c a W bozon Compton-sugara. Az ω körfrekvenciájú forgás kerületi sebessége c = ωr, ezért a sugárnövekedés a körfrekvencia csökkenésével jár az

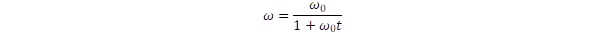
egyenlet szerint, ahol az ω₀ frekvencia a W bozon m₀ tömegéből számolható a ℏω₀ = m₀c² ekvivalencia elv alapján. A frekvenciacsökkenés a tömeg, illetve a részecske energiájának csökkenését hozza magával. A W bozon kísérletileg meghatározott tömegét ezért lokális képződési tömegnek kell értelmezni és nem nyugalmi tömegnek, hiszen a fénysebességű terjedés miatt a kölcsönhatási bozon nem lehet nyugalomban. A fotontól eltérően mégis jogunk van tömegről beszélni, mert a W bozon energiája és az ennek megfelelő E/c² tömege a tér egy szűk tartományára lokalizálódik. A W bozon fokozatosan csökkenő körfrekvenciája teszi számára lehetővé, hogy a részecske átalakítás „csavarkulcsa” legyen, mert kapcsolatot teremthet a különböző tömegű – azaz forgási frekvenciájú –  részecskék között.

Az átalakulások mellékterméke: a neutrínó

 Nem ejtettünk még szót az átalakulás másik részecskéjéről, a neutrínóról, amit a folyamat „hulladék anyagának” tekinthetünk. Ennek nincs sem nyugalmi tömege, sem töltése. A Fermion-egyenlet általánosításával kapcsolatban hasonlítottuk össze az elektront és a neutrínót (Lásd: „A Dirac-egyenlettől az általános fermion egyenletig”). Az előbbinek van saját tömege és töltése, de nincs saját impulzusa, míg az utóbbi rendelkezik saját impulzussal, de nincs sem tömege, sem töltése. Épp a saját impulzus teszi lehetővé, hogy létezhetnek különböző tulajdonságú neutrínók, amit elektron, müon illetve tau típusú neutrínónak nevez a szakirodalom, és ezek egymásba alakulási folyamata a neutrínó oszcilláció („A neutrínó kalandos története”).

Honnan származik a W bozon óriási tömege?

A gyenge-kölcsönhatás első lépésének van egy különös tulajdonsága: a képződő W bozon tömege, sokkal nagyobb, mint a forrás, jelen esetben a müon saját tömege, de ez igaz a többi átalakulási folyamatban is, így például a neutron béta-bomlása során. Ezt is magyarázza a fénysebességű forgásmodell, mely szerint a tér a forgási frekvencia mértékében torzul negatív potenciális energiát létrehozva , amely ellensúlyozza a forgás kinetikus energiáját, azaz a potenciális energia és a mozgási energia összege mindig nulla marad („A fizikai világ két arca: A látható és a láthatatlan”). A forgás lassulását úgy kell értelmezni, hogy a csatolás erőssége a részecske és a tér között fokozatosan csökken.

Az impulzus szerepe az átalakulásban

Az átalakulási folyamatban szó kell, hogy essék az impulzusról is! A kilépő neutrínó impulzussal rendelkezik, ezt a megmaradási elv szerint a W bozon saját impulzusa egyenlíti ki. Mivel fénysebességű terjedésről beszélünk ez a saját impulzus a pc = E összefüggésből határozható meg, hasonlóan a fotonhoz. Az impulzus viszont irányfüggő mennyiség, ezért a W bozon terjedésének van egy kitüntetett iránya is. Ez a polarizációs irány játszik fontos szerepet az átalakítási folyamat második lépésében. Ez a lépés az első megfordítása, ebben a W^– bozon átalakul elektronná egy második neutrínó kibocsátása mellett, de ez már jóval kisebb energiával történik, mert a spirálmozgás során a körfrekvencia lecsökkent. De mekkora ez a csökkenés? Nézzük meg a forgás fázisának változását, amit a frekvenciaváltozása miatt integrálással határozhatunk meg:

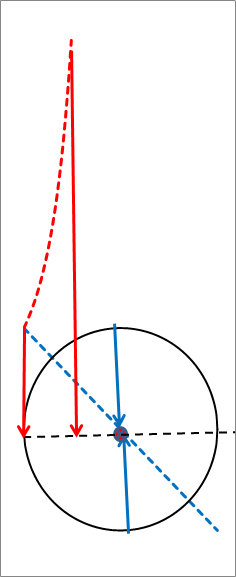
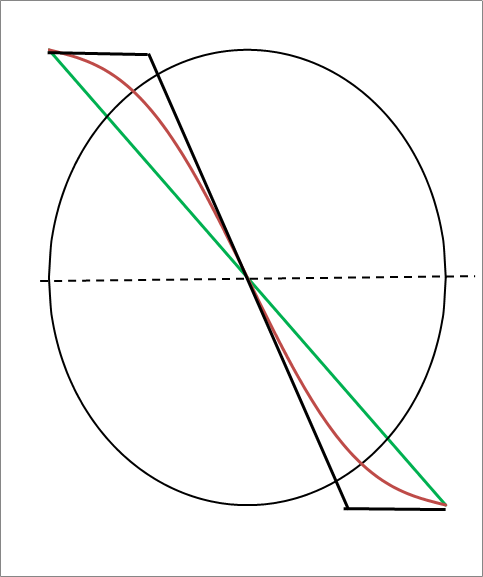
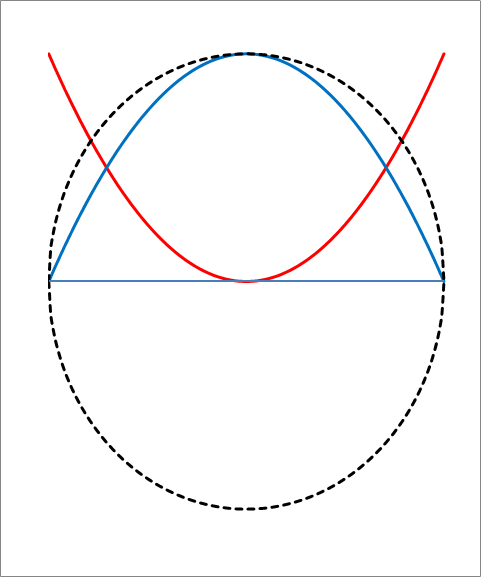
A fázis változását a sugár függvényében logaritmikus skálán mutatja az ábra.

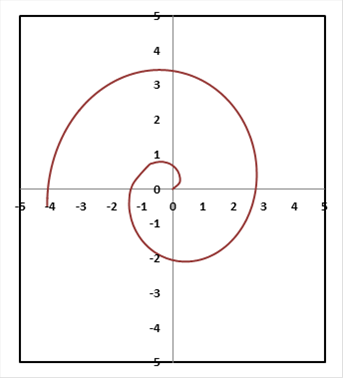
A W bozon spirális pályája logaritmikus ábrázolásban, a fekete nyíl a tau, a zöld a müon, a piros az elektronkilépés pozícióját mutatja

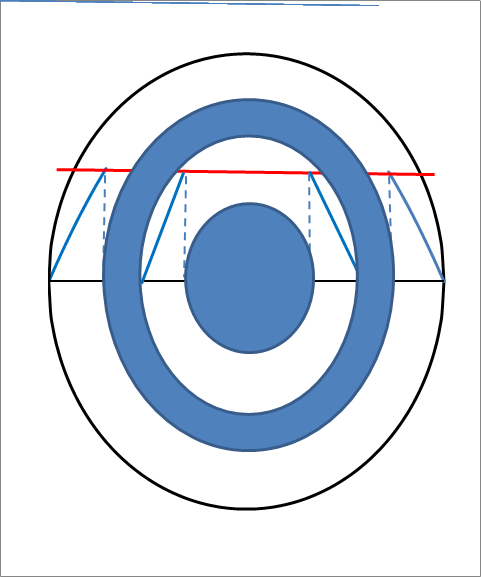
A W bozon aktív fázisai

A következő kérdés, hogy mekkora fázisnál következik be a második lépés? Ezt jelöli ki a W bozon kezdő iránya: akkor jön létre átalakulás, amikor egy-egy félfordulat bekövetkezik, ugyanis ekkor az impulzus újra az eredeti iránnyal lesz párhuzamos. Tehát minden egyes π szögű elfordulásnál jöhet létre a két új részecske. Vezessük be a ρ = 1 + ω₀t tömegcsökkenési arányt, ami π szögű elfordulásnál e^π = 23,14 nagyságú lesz. Ez azt jelenti, hogy amikor az eredeti tömeg ilyen mértékben csökken, bekövetkezhet a W bozon átalakulása. Ezt is szemlélteti az ábra. A W bozon induló energiája E₀ = 80,395 GeV a mérések szerint, ez lecsökken az első félfordulat után E₁ = 3,4738 GeV, a másodiknál E₂ = 150,1 MeV, a harmadiknál E₃ = 6,487 MeV értékre. Ezen az energián osztozik a létrejövő két fermion. Az elektron, müon és tau részecske esetén az m_i nyugalmi tömegből számíthatjuk az energiát, míg a neutrínónál a p_i saját impulzust kell alapul venni:

Itt E_Kin a képződő részecskék mozgási energiája. A W bozon eltűnése után visszaáll az eredeti energia (helyreáll az energiamegmaradás törvénye), ezért az határozza meg, milyen részecske szabadul ki a W bozonból, hogy melyik saját energiája van közel a félfordulatok E_i értékéhez. Mivel a tau részecske energiája 1,77682 GeV , azaz E₁ fele, így ez a részecske a W bozon első félfordulatánál jön létre, míg  a tau neutrínóra maradó energia maximum 1,697 GeV lehet, tehát a részecskék közel egyformán osztoznak a bozon E₁ energiáján. (Itt a számításnál nullának vettük a kinetikus energiát).  A müon saját energiája 105,568 MeV, ezért ez már egy teljes fordulat után jön létre, a müon neutrínóra jutó energia pedig 44,53 MeV lesz, tehát kisebb, mint a müon saját energiája. Végük az elektron saját energia 0,511 MeV a harmadik félfordulat után jön létre, és ekkor a neutrínóra maradó hányad jóval nagyobb lehet: 5,976 MeV. A nagyságrendi változásból látható, hogy a részecskék tömege a W bozon tömegcsökkenéséhez igazodik. A W bozon a három félfordulat után megszűnik, mert az elektron stabilis részecske és spontán módon nem bocsát ki újabb W bozont, csak akkor, ha például pozitronokkal bombázzuk.

A hadronok bomlása

A leptonok bomlásánál lényegesen bonyolultabb a kvarkokból felépülő mezonok (kvark + antikvark) és a barionok (három kvark, vagy három antikvark) bomlási mechanizmusa. Ennek egyrészt azaz oka, hogy a kvarkok nincsenek sem tömeg, sem impulzus sajátállapotban („A Dirac-egyenlettől az általános fermion egyenletig”), másrészt az összetett hadronokban (ez a barionok és mezonok összefoglaló neve) az erős és az elektromágneses kölcsönhatás fontos szerepet játszik. A kvarkoknak két típusa van a 2/3e töltésű u, és a –1/3e töltésű d, és a leptonokhoz hasonlóan három generációjuk létezik, melyek csak a tömegükben különböznek (pontosabban a renormált tömegükben, mert szabad kvark nem figyelhető meg). Az u-típus két magasabb generációja a c és a t kvark, a d-típusé az s és a b nevű kvark. A kvarkok három generációjának renormált tömege nagyságrendileg igazodik a W bozon három aktív állapotához: u és d E₃-mal, c és s E₂-vel, míg b E₁-el összemérhető nagyságú. Kilóg a sorból a nagy tömegű t kvark, evvel függhet össze, hogy olyan hadron nem létezik, amelyben a t kvark lenne az egyik összetevő.

Béta-bomlás

Hadronoknál az számít kivételnek, amikor a gyenge-kölcsönhatás hozza létre a bomlást, mert az elektromágneses hatás 10 nagyságrenddel gyorsabb folyamat. Ezért amikor a két kölcsönhatás együtt játszik szerepet a gyenge-kölcsönhatás nem figyelhető meg. Barionoknál a két nukleon (proton és neutron) külön esetet képvisel nagy stabilitásuk miatt, a proton (uud) spontán módon nem bomlik, csak neutrínó sugárzással hozható létre átalakulás, míg a neutron (udd) bomlásának felezési ideje 880 s. A proton stabilitását az okozza, hogy a barionok között ez a legkisebb saját energiával rendelkező részecske, neutron pedig azért stabil, mert az elektromágneses kölcsönhatás nem idéz elő bomlást.  Ennek oka, hogy a töltéssel nem rendelkező gamma-sugarak nem változtathatják meg a részecskék töltését. Neutron béta bomlásakor proton jön létre, amit elektron és elektron neutrínó kibocsátása kísér, azért épp ezek a részecskék lépnek ki, mert a neutron és proton közötti 1,3 MeV energiakülönbség nem elegendő müonok létrehozásához.  A béta bomlás tehát kvark-kvark átalakítási folyamat  W^– bozon közvetítésével:

u → d + W^–→ d + e^– + ν_e

Mezonok bomlása

A mezonok családjában az ud összetételű +e töltésű pion a legstabilabb, melynek a legkisebb a tömege (139.6 MeV/c²) a mezonok között. Ez a tömeg egyrészt összemérhető a W bozon E₂ energiájával, másrészt nagyobb a müon tömegénél, ami magyarázza a kvark kombináció átalakulását  müonra és müon neutrínóra:

ud → W⁺ → μ⁺ + ν_e

Ekkor a gyenge kölcsönhatás egy kvark-antikvark kombinációt alakít át leptonokra. Hasonló bomlási folyamata van az us összetételű +e töltésű kaonnak is, ahol a saját energia (493 MeV) szintén müon generálására elegendő.

Elektronbefogás

Szintén a gyenge kölcsönhatás hozza létre az elektron-, vagy más néven K- befogást. Az atomokban kötött elektron a nulla impulzusmomentumú „ s” pályákon véges valószínűségsűrűséggel van jelen az atommagban anélkül, hogy az elektromos vonzás miatt a pozitív atommag befoghatná az elektront. Ha azonban az atommagban több a proton, mint a stabilis izotópban, akkor a gyenge-kölcsönhatás miatt létrejöhet befogás. Ekkor az atom rendszáma lecsökken. Példaként nézzük a ²⁶Al atommagot! Ebben 13 proton és 13 neutron van, viszont a stabilis ²⁷Al izotópban már eggyel több a neutron. Az elektronbefogás miatt eggyel csökken a protonok, és eggyel nő a neutronok száma, és létrejön a ²⁶Mg izotóp. Ez annak felel meg, hogy a gyönge-kölcsönhatás az egyik u kvarkot átalakítja d kvarkká W⁺ bozon közvetítésével, amelyik a második lépésben elnyeli az elektront:

u + e^– → d + W⁺ + e^– → ν_e + d

A rádióaktivitásnak ez a formája eltér az egyéb folyamatoktól, mert ha megfosztjuk az atomokat az elektronoktól (teljes ionizáció), akkor nem jön létre az atommag átalakulása, azaz nem lesz többé radioaktív a szóban forgó izotóp.

A Z bozon színre lépése

A gyenge-kölcsönhatás nem minden esetben alakítja át a részecskét, de szerepe mégis tetten érhető. Buborékkamrában vizsgált elektronoknál azt tapasztalták, ha jelentős neutrínó fluxus halad át a kamrán, akkor egyes elektronok mozgása hirtelen megváltozik (Carlo Rubbia, Simon van der Meer, Nobel díj: 1984). Ezt úgy lehetett értelmezni, hogy az elektron lökést kaphat a neutrínóktól, amit viszont csak semleges bozon idézhet elő, ami a Z elnevezést kapta. A Z bozon tömege 91,2 GeV/c² még a W bozonét is meghaladja, ez képessé teszi, hogy átadja impulzusát az elektronnak. A szakirodalom a folyamatot rugalmas neutrínó szórásnak nevezi, mert ennek során nem alakul át a meglökött elektron más részecskévé. A fénysebességű forgásmodell úgy értelmezi a Z bozont, mint két ellentétes kiralitású spirális szuperpozícióját. A W bozonhoz hasonlóan a semleges Z bozon is rendelkezik saját impulzussal.

A blog további írásai rövid összefoglalóval együtt elérhető: „Paradigmaváltás a fizikában” című bejegyzésben.

Ha valaki Nobel díjat szeretne kapni, annak érdemes foglakozni a neutrínók fizikájával. Ezt mutatja, hogy eddig négy alkalommal ítélték oda a díjat nyolc fizikusnak a területen elért eredményekért, de több is lehetett volna, ha a kutató megérhette volna a nagy napot.

A neutrínó felfedezése

A részecske felfedezése Wolfgang Paulinak köszönhető 1930-ban, aki szintén Nobel díjas, de az elismerést nem ezért kapta. A radioaktív béta-bomlásnál figyelt fel arra, hogy az elbomló atomból távozó elektron nem viheti magával sem az összes energiát, impulzust és a spint sem, ezért szükség van a magyarázathoz egy S = ½ spinnel rendelkező töltés nélküli részecskére, aminek eredetileg a neutron nevet adta. Két évre rá James Chadwick angol fizikus fedezte fel, hogy létezik egy másik semleges részecske is, ami az atommag alkatrésze, amit ő is neutronnak nevezett el. Először vitatott volt, hogy két különböző részecskéről van-e szó, de aztán Enrico Fermi (Nobel díjas, de szintén más eredményért díjazták) olasz fizikus adta meg a kapcsolatot a két részecske között, amikor a béta-bomlást úgy értelmezte, hogy a neutron protonná alakul, miközben egy elektron és egy neutrínó (ekkor kapta meg az új nevet a részecske) lép ki belőle. Chadwick 1935-ben kapott Nobel díjat a neutron felfedezéséért, de ez még a neutrínó előtörténetéhez tartozik az említett négy díjon felül.

A neutrínó láthatóvá tétele

Egészen 1956-ig a neutrínót „láthatatlan” részecskének tekintették, ami arra szolgált, hogy a különböző megmaradási törvények rendben legyenek, de ekkor két amerikai fizikus, Clyde Cowan és Frederick Reines, gondolt egy nagyot és a béta-bomlás megfordításával (béta-befogás) láthatóvá tette ezeket a rejtélyes részecskéket is. A megfordítás azt jelentette, hogy a béta-bomláskor képződő antineutrínót (a részecske-antirészecske terminológiában nevezik így) befogja egy proton, ami által neutron képződik egy pozitron kilépése mellett. Tulajdonképpen a pozitron kilépés segíti a neutrínó detektálását, de a mérésnél különleges elővigyázatosságra van szükség, mert a kozmikus sugárzás, vagy a rádióaktivitás is létrehozhat pozitront. Ezért csak a föld mélyén jól árnyékolt környezetben végezhető el a mérés. Ráadásul a neutrínó igen gyengén reagál más részecskékkel, amit avval szokás jellemezni, hogy egy fényév hosszúságú, tehát a Naprendszer legkülső határáig érő ólomfalra lenne szükség, hogy a neutrínók felét elnyelje. A Nobel díj bizottság csak sokkal később ismerte fel a felfedezés jelentőségét, amiért 39 évvel később 1995-ben ítélte meg a díjat, amit már csak Reines kaphatott meg, aki még három évig élt a díj átvétele után.

Többféle neutrínó létezése

De mégsem az 1995-ben átadott díj volt az első, amivel a neutrínó kutatást jutalmazták, hanem az 1988-as. Ebben az évben két amerikai (Leon Lederman és Melwin Schwartz) és egy német tudós (Jack Steinberger) részesült a megtiszteltetésben, mert kimutatták, hogy az elektronnal sokban egyező, de jóval nagyobb tömegű müonok bomlásakor szintén kilép egy a neutrínó tulajdonságait hordozó részecske. Nem sokkal később, 1990-ben a Fermilab tudósai mutatták ki, hogy a müonnál is jóval nagyobb tömegű tau részecske bomlása is egy újabb neutrínó kibocsátásával történik. Az elemi részecskék tulajdonságait összegző Standard Modellben ezért a leptonok családjában már három elektrontípusú és három neutrínóhoz hasonló részecske szerepel. De amíg az elektron, müon és tauon esetén a tömegek nagy különbsége világosan elhatárolja egymástól a részecskéket, addig a neutrínók esetén nem volt világos, hogy ezek a részecskék igazából miben is különböznek, mert eredetileg tömeg nélkülieknek tartották a neutrínókat. Ennek oka, hogy a mérési pontosság határain belül a neutrínók mozgási sebessége azonosnak adódott a fénnyel, márpedig ekkora sebességgel csak nulla nyugalmi tömegű objektumok mozoghatnak. Szintén nyitott kérdés maradt, hogy létezik-e külön neutrínó és antineutrínó, ahogy az elektronnak és van antirészecske párja, a pozitron.

Szoláris neutrínó deficit

Ezek a kérdések a részecskék alaptulajdonságait érintik, ezért a neutrínók viselkedésének megértése a fizikai kutatás homlokterébe került. Új és új módszereket fejlesztettek ki, hogy minél megbízhatóbban mutassák ki a neutrínókat. Ebben értek el jelentős eredményeket az amerikai Ray Davis és a japán Masatoshi Koshiba, akik a neutrínók földön kívüli forrására voltak kíváncsiak, és főként a Nap felől érkező fotonok mennyiségének (fluxusának) meghatározására törekedtek. Ezt ismerte el a Nobel díj bizottság 2002-ben. Eredményeiket azt tette különösen fontossá, hogy kiderült egy anomália. A Nap fúziós folyamataira épített elméletből meg lehetett becsülni, hogy onnan mekkora neutrínó fluxus érkezik a Földre, de tapasztalataik szerint ennek csak felét-harmadát lehetett módszerükkel megfigyelni. Ez azért volt meglepő, hiszen a neutrínók mindenen könnyen áthatolnak, így a veszteség oka nem volt érthető. Először a napmodell hibájára gyanakodtak, de ezt hiába igyekeztek finomítani ettől nem csökkent az eltérés a mért és a számított fluxusok között.

A neutrínó oszcilláció színre lépése

Itt lép be a képbe a neutrínó kutatás különös egyénisége Bruno Pontecorvo, olasz származású tudós. Tudományos karrierjét még Fermi laboratóriumában kezdte, de Mussolini hatalomra jutása után, 1940-ben Párizsban folytatta tevékenységét, majd onnan a német megszállás elől menekülve az Egyesült Államokba emigrált. Ott sem tartózkodott hosszú ideig, Kanadába ment, majd az angol állampolgárság megszerzése után Angliában folytatta tevékenységét. Kutatási területe a magfizika volt és ezen belül is a neutrínó kutatás volt a fő területe. Kollégái ezért a Mr. Neutrínó névvel is illették őt.  1950-ben azonban egy római utazás során eltűnt és csak néhány évvel később derült ki, hogy családjával együtt a Szovjetunióba szökött. Haláláig Dubnában folytatta tevékenységét és ebben az időszakban érte el azokat az eredményeket, amely nagy lökést adott a neutrínók tulajdonságainak feltárásához. Ennek ellenére Nobel díjban nem részesült, amiben része lehetett a gyanúnak, hogy kémtevékenységet folytathatott a hidrogénbomba megvalósítása érdekében, bár ezt ő tagadta, sőt éppen a békés célú kutatás mellett állt ki, bizonyíték azóta sem került napvilágra  esetleges kémtevékenységéről.

De mi is volt, amit Pontecorvo hozzátett a neutrínó elméletéhez? A Standard Modell egyik tézisével szemben, amely szerint a neutrínónak nincs tömege, felvetette, hogy mindhárom neutrínó típusnak van tömege és a neutrínó három formája között oszcillációk jönnek létre. Ez a lassú oszcilláció szuperponálódik a neutrínó és az antineutrínó közötti gyors oszcillációra. A Napban keletkező neutrínók eredetileg elektron típusúak, de ez az oszcilláció révén részben átalakul müon és tau típusú neutrínóvá, és emiatt a Földre érkező neutrínó áramban már lecsökken az elektron neutrínók mennyisége. A mérőműszer alapvetően csak az elektron neutrínókat észleli és így a vártnál alacsonyabb lesz a mért fluxus. De hogyan mozoghatnak fénysebességgel a neutrínók, ha van nyugalmi tömegük? Erre a válasz, hogy minden mérés véges pontosságú, és a neutrínók sebessége nagyon közel lehet a fényhez, mégpedig annyira, hogy az eltérés már belül van a hibahatáron. Ha ismerjük ezt a kis eltérést és tudjuk a neutrínó energiáját, akkor már kiszámíthatjuk a nyugalmi tömeget, ami annál kisebb minél közelebb vagyunk a fénysebességhez. A növekvő pontosságú mérések miatt egyre lejjebb kellett szorítani a neutrínók lehetséges tömegét és ma már ott tartunk, hogy a neutrínók tömege legalább egymilliószor kisebb, az egyébként legkisebb tömegű részecskének tartott elektronnál is. Ezen a parányi tömegen belül is meg kell különböztetni a müon és a tau neutrínó tömegét az elektron típusú részecskétől, és mivel a nagyobb tömegű neutrínók kissé lassabban haladnak, így amikor a háromféle neutrínó hullámai szuperponálódnak, olyan lebegés jön létre, amelyben periodikusan változik a neutrínó áramon belül a három komponens aránya. Az L lebegési periódushossz az energiából és a tömegkülönbségek négyzetéből számolható az

összefüggés szerint. Pontecorvo a három neutrínóhoz kvantummechanikai „tömeg sajátállapotot” rendelt, amelynek háromdimenziós terében írta le a lehetséges keveredési állapotok oszcillációját. Ezt nevezi a szakirodalom PMNS mátrixnak az elmélet megalkotóinak neve alapján, mert ennek kidolgozásához három japán tudós (Maki, Nakagawa és Sakata) is hozzájárult.

A neutrínó oszcilláció bizonyításához a Napból származó részecskéken kívül tanulmányozták az atmoszféra felső határán a kozmikus sugárzás által keltett müonok neutronjait is, valamint érdekes adatokhoz lehetett jutni a szupernóva robbanásból származó neutrínók tanulmányozásával is. A különböző irányú mérések alátámasztották a neutrínó oszcilláció elméletét, amiért a legfontosabb bizonyítékokat szolgáltató japán Takaaki Kajitát és az amerikai Arthur Mc Donaldot a Nobel díj bizottság 2015-ben tüntette ki. További három tudós, akik ugyan nem kaptak Nobel díjat, de érdemes nevüket megemlíteni, kimutatták a neutrínók egy további fontos tulajdonságát. A fénytörés magyarázatánál jól ismert, hogy optikai közegekben a fotonok és a töltött részecskék kölcsönhatása miatt a fény lassabban terjed, mint vákuumban. Ehhez hasonló, de sokkal kisebb hatás lép fel a gyenge kölcsönhatás miatt a neutrínók és fizikai közegek között. Ezt két szovjet (Sztanyiszláv Mikhejev és Alekszej Szmirnov) és egy amerikai tudós (Lincoln Wolfenstein) mutatták ki. Rájuk utalva nevezik a jelenséget MSW effektusnak. Itt a hullámok koherencia hossza játszik szerepet, mert a sebesség változása a hullámok fázisát és ezáltal az oszcillációt is érinti.

Új magyarázat a neutrínó oszcillációra

Egy korábbi írásomban („Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók”) már rámutattam arra, hogy nullatömegű neutrínókkal is lehet magyarázni az oszcillációt a háromféle neutrínó között. Ehhez a fermionokra általánosított relativisztikus Dirac-féle hullámegyenletet hívtam segítségül (lásd: „A Dirac-egyenlettől az általános fermion egyenletig”). Itt csak a gondolatmenet vázlatát ismertetem, ami alighanem csak a kvantummechanikában otthonosan mozgó fizikusok számára lesz érthető.

Az elektron relativisztikus mozgásegyenlete

 A kiindulópont a relativitáselmélet alapját képező kovariancia elv. Az energia tekintetében ez azt jelenti, hogy négyzetes összefüggés írható fel az energia és annak két komponense között, melyek közül az egyik az impulzussal kifejezett mozgási energia, a másik a nyugalmi tömeghez tartozó m₀c² energia. Elektromágneses mezőben ezt egészíti ki a mágneses hatásokat leíró vektorpotenciál és az elektrosztatikus hatást megadó skalárpotenciál. Az előbbi a kinetikus energiához ad járulékot, az utóbbi közvetlenül a teljes energiát egészíti ki. Amikor a kvantummechanikára térünk át, akkor az energia lineáris összefüggését keressük az egyes tagoktól, ezért a kovariancia kifejezéséből négyzetgyököt kell vonni. Ezt oldotta meg Dirac, amikor a műveletet négydimenziós mátrixokkal, azaz spinorokkal hajtotta végre. Mivel a kinetikus tag vektoriális ez önmagában három tagot jelent, amihez negyedikként járul hozzá a nyugalmi energia. Ez magyarázza, hogy négydimenziós mátrixokkal lehet felbontani a négyzetgyököt és a kapott eredmény négy csatolt lineáris differenciálegyenletre vezet.

Az energia kétértékűségei

A kovariancia kérdését azonban más oldalról is megközelíthetjük. Amikor négyzetre emelünk, eltűnik az eredeti előjel, mert a negatív és pozitív számok négyzete azonos. A kovariáns kifejezésben három tag van a teljes energiával együtt, ezért háromféle alternatíva jelenik meg. Mi ennek az eredete? Ez részben az időhöz és részben a tér szerkezetéhez kapcsolódik. Amikor egy haladómozgás forgással jár együtt, akkor energetikailag nem tudunk különbséget tenni a két lehetséges forgásirány között. A másik, hogy a mozgást két időirányból is megközelíthetjük: következtethetünk a jelenből a jövőre, de fordítva is gondolkozhatunk, ha a jelen irányából a mozgások múltjára vagyunk kíváncsiak. Voltaképp ez a két alternatíva jelenik meg a Dirac-egyenletben is, az egyik a spin kétdimenziós tere, a másik az energiának adhat akár pozitív, akár negatív előjelet. Ennek eredete világosan látszik az energia operátor szerkezetéből, ami az energiát az idő-szerinti differenciálhányadossal fejezi ki. Van azonban egy harmadik alternatíva is: a koordinátatengelyek sodrásirányát választhatjuk jobb és balsodrásúnak is, ettől az energia nem fog megváltozni. Ezt a szimmetriát nevezzük kiralitásnak. Annak érdekében, hogy ezt a kettősséget is bevonjuk a formalizmusba már nyolcdimenziós spinorokra van szükség. A Standard Modell három részecske típusa: az egész töltésű elektron csoport, a nulla töltésű neutrínók és a törttöltésű kvarkok éppen ebben a királis térben értelmezhetők. Matematikailag ez úgy valósítható meg, ha az egyes kétdimenziós tereket a kétdimenziós Pauli mátrixokkal írjuk le, és ezek segítségével operátorként definiáljuk a tömeget és a töltést is. Evvel a kvantummechanika mélyebb szintjét hozhatjuk létre, mert ettől kezdve már valamennyi mérhető fizikai mennyiség operátoros alakban jelenik meg.

Mikor mérhetők pontosan a fizikai mennyiségek?

Amikor mátrixokkal adjuk meg valamilyen fizikai mennyiség operátorát, akkor az állapotfüggvény terében képzett diagonális mátrix mutatja, hogy a mérés pontos értéket adhat-e a mennyiségnek, ezek a sajátértékek. Ellenkező esetben csak valószínűségi kijelentéseket tehetünk és várható értékről beszélünk. A Pauli mátrixok esetén ezért a

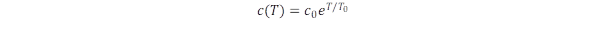
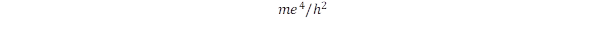
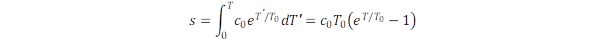
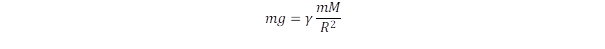
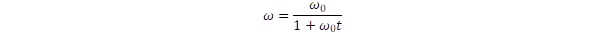
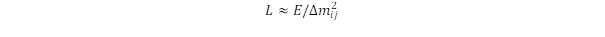
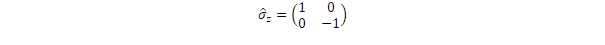komponensnek különös jelentősége van. A másik szélső példa, amikor nullák a diagonális elemek

,

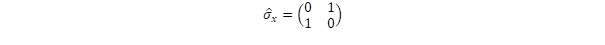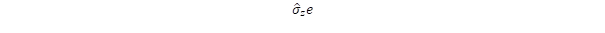ekkor a szóban forgó fizikai mennyiség várható értéke nulla lesz.

Amikor az általános fermion egyenletet elektronokra alkalmazzuk a töltésoperátor mátrixa

,

míg a tömegé

 lesz, azaz a részecskéhez egyaránt rendelhetünk töltést is, meg tömeget is. Az impulzus operátorában viszont a

nem-diagonális mátrix jelenik meg, ez azt jelenti, hogy az elektronnak nincs saját impulzusa (a várhatóérték nulla, ha a részecske nem mozog). A két Pauli mátrix sorrendje nem cserélhető fel (szorzatuk antiszimmetrikus), erre vezethető vissza a Dirac egyenletben, hogy a részecske tömege megnövekszik a sebesség függvényében. Hasonlítsuk ezt össze a neutrínóval. Ekkor a kép megfordul, akár a töltésről, akár a tömegről van szó, ott a nem-diagonális

Pauli mátrix jelenik meg, azaz mind a töltésnek, mind a tömegnek nulla lesz a várható értéke. Ez magyarázza, hogyan mozoghat a neutrínó fénysebességgel. Evvel szemben az impulzus mátrixát a diagonális Pauli mátrix definiálja, azaz a neutrínó rendelkezi saját impulzussal. A háromféle neutrínó tehát nem abban különbözik, hogy eltér a nyugalmi tömegük, hanem abban hogy rendelkeznek háromféle saját impulzussal. A részecskék hullámtermészete miatt az impulzushoz hullámhosszat rendelhetünk, ami a fénysebességű mozgás miatt λ = h/p_i lesz, ahol az i index jelöli az egyik neutrínót. Ebből következik, hogy a lebegési hossz 

 alakban adható meg. Az oszcillációs keveredést leíró PMNS mátrixelméletet ez a különbség azonban nem érinti.

Melyik modell van összhangban a kísérleti megfigyelésekkel?

Összehasonlítva az oszcillációs hossz kifejezését a Pontecorvo elmélettel, egyrészt a tömegnégyzetek helyett a saját impulzusok lépnek fel, másrészt esetünkben nem függ a hossz az energiától. Mit lehet mondani a kísérleti tapasztalatok alapján az oszcillációs hossz energiafüggéséről? A problémát az jelenti, hogy eddig nem sikerült a neutrínó fluxus periodikus változását megfigyelni, csak arról van tapasztalat, hogy mikor lép fel neutrínó deficit. A Napból érkező neutrínóknál a deficit független attól, hogy a Föld éppen milyen távol van a Naptól, pedig a keringés során a távolság 147 és 152 millió kilométer között változik. Ha periodikusan változó összetételt tételezünk fel, akkor a hullámhossznak legalább 10 millió kilométernek kell lenni. Más mérések során, így az atmoszférában képződő müonok bomlásakor képződő neutrínóknál azt találták, hogy a „felülről” érkező neutrínó fluxus nagyobb, mint ami „alulról” a Földön áthaladva érkezik. Mivel a Föld minimális mértékben nyeli el a neutrínókat, így a különbség az oszcillációval magyarázható, de ekkor a Föld átmérőjénél rövidebb lehet csak az oszcillációs hossz, tehát a korábbi becslésnél ezerszer rövidebb értéket kapunk. Ez úgy értelmezhető, hogy az oszcilláció a koherencia elvesztése miatt csillapodik és a keveredési arány bizonyos távolság után már nem változik. Emiatt a megfigyelések alapján csak a koherencia hosszról kapunk információt és nem dönthető el, hogy a neutrínók eltérő tömegére, vagy a neutrínó saját impulzusára alapuló modell írja le helyesen az oszcillációs jelenséget. A saját elképzelésem mellett szól, hogy egységes leírást ad a fermionokra és azon a kísérleti tapasztalaton alapul, hogy a neutrínók fénysebességgel mozognak.

A blog korábbi írásai a „Paradigmaváltás a fizikában” című bejegyzésen keresztül érhetők el.

Einstein általános gravitációs elméletének egyik izgalmas következménye a fekete lyukak létezése, amit később a csillagászati megfigyelések fényesen igazoltak. De valóban csak Einstein elméletéből következik, hogy léteznek fekete lyukak?

Newton egyenlet

Induljunk ki Newton gravitációs egyenletéből, amivel értelmezni lehet a bolygókeringés törvényeit. Ha a bolygó tömege nagyon kicsi a Naphoz képest és körpályákra szorítkozunk, akkor a centrifugális erőt egyensúlyban tartó gravitációs erő:

Az egyenlet egyik oldalán szerepel a tehetetlen tömeg, a másikon a gravitáló tömeg. A kettő egyenlősége miatt az egyenlőségből az m tömeg kiesik, és azt kapjuk, hogy

A sebességet meghatározó összefüggés ezért alkalmazható bármilyen kicsi is legyen a keringő tömeg, vonatkozik ez a fényre is, annál is inkább, mert az m = E/c² összefüggés szerint a fotonhoz is rendelhető mozgási tömeg. A foton viszont fénysebességgel mozog, ezért akkor kerül „kötött” pályára az M tömeg körül, ha

Itt a fénysebesség c = 3x10⁸ m/s és a gravitációs állandó G = 6,673x10^-11 m³/kg×s². (A relativitáselméletben a 2R_f sugár felel meg az eseményhorizontnak, mert ennél az értéknél az Einstein egyenletnek szingularitása van. Ez a kettes faktor a további meggondolások alapjait azonban nem érinti.)

Van egy másik feltétele is a fekete lyuk kialakulásának, mert az M tömeget magába záró objektum R_M sugara nem lehet nagyobb, mint a kötött foton pályasugara, azaz

A feltételek teljesüléséhez nem csak extrém nagy tömegsűrűség kell, hanem megfelelő méret is. Azonos sűrűségű égitesteknél azért kedvezőbb a nagyobb méret a fekete lyuk kialakulásához, mert a tömeg R_M harmadik hatványával növekszik, míg az R_f pályasugár arányos a tömeggel.

Milyen csillagok lehetnek fekete lyukak?

Nézzük meg a feltételek teljesülését különböző égitesteknél! A Föld esetén a csapdázott foton pályasugara kisebb, mint 5 milliméter, a Napnál pedig 1,5 km körül van, ami jóval kisebb az égitestek kiterjedésénél. A Földre vagy Napba érkező fényt ezért nem a gravitáció fogja foglyul ejteni, hanem az égitestek felületen nyelődik el, és az égitestek felszínéről kibocsátott fénysugarak zavartalanul távozhatnak. A galaktika óriáscsillagai sem viselkedhetnek fekete lyukként, mert a tömegükhöz tartozó pályasugár nem haladja meg a 200 kilométert, amelynél saját sugaruk sok nagyságrenddel nagyobb.  A fekete lyukhoz szükséges nagy sűrűséget sokkal inkább a neutroncsillagoktól várhatjuk. Ezeknek tömege 1 és 3 Naptömeg között változik és sugaruk 10 km körül van. Egy közepes neutroncsillag 3x10³⁰ kg tömegét alapul véve a sűrűség 6x10¹⁷ kg/m³-nek adódik, míg a kötött foton pályasugara 2,5 km körül lehet. Ebből látható, hogy a 10 km sugarú neutroncsillagok sem viselkednek fekete test gyanánt.

A nukleonok tömegsűrűsége

Mielőtt továbblépnénk, érdemes elgondolkozni rajta, hogy mi határozza meg a neutroncsillagok, illetve a fekete testek tömegsűrűségét. Induljunk ki a nukleonokból, a protonból és neutronból. A szóráskísérletek szerint a proton sugara r_p = 0,87x10^-15 m, tömege pedig m_p = 1,66x10^-27 kg, az ebből számolható sűrűség ρ_p = 6x10¹⁷ kg/m³, egyezően a neutroncsillagoknál becsült értékkel. Tehát a neutroncsillag olyan mint egy sűrűn pakolt hatalmas neutron tömb! Érdemes azt is megjegyezni, hogy ez a sűrűség meghaladja a nagyobb atommagok sűrűségét, ami 3x10¹⁷ kg/m³ körül van. A Standard Modell szerint egyaránt az erős kölcsönhatás tartja egyben a kvarkokat a nukleonokban, és a nukleonokat az atommagokban. A sűrűség csökkenése nagyobb atommagoknál részben az erős kölcsönhatás rövid hatótávolságának, részben a protonok közötti elektrosztatikus taszításnak tulajdonítható.

Egy kis kémia

Az atommagok szerkezetének megismeréséhez segít, ha párhuzamot vonunk az atomi elektronpályákkal. Az elektronok héjakba rendeződnek, mert a spinhez két, az L impulzusmomentumhoz 2L +1 azonos energiájú pálya tartozik, és a Pauli elv szerint minden pályán csak egyetlen elektron lehet. Ez vezet a molekulák kialakulásához, mert az egyik atom zárt héja feletti többletelektronját átadhatja egy másik atomnak, ahol a héjból egy elektron hiányzik, ez az ionos kötés.  Ennél sokkal fontosabb azonban a kovalens kötés, ahol az atomok „megosztoznak” az elektronokon kölcsönösen kialakítva zárt héjakat. Ennek „nagymestere” a szén, amelynek vegyértékhéja félig van tele, azaz félig üres, és ebből fakad, hogy a szerves vegyületek végtelen sokasága jön létre.

Egy kis magfizika

Az atommagot alkotó protonok és neutronok is héjakba rendeződnek, de itt nagyságrendekkel nagyobb az energia és sokkal kisebb a nukleonok közötti távolság. Erre szükség is van, mert az erős kölcsönhatásnak rövid a hatótávolsága. Az atomok szerkezetének kialakításában három erő: az erős- és gyengekölcsönhatás, valamint az elektromágneses erő összjátékára van szükség. Az erős kölcsönhatás nem tesz különbséget a nukleonok között, egyforma erővel köt össze két protont, két neutront, vagy egy protont és egy neutront. De akkor miért nem jönnek létre már normál körülményeink között is neutron agglomerátumok, hiszen ekkor nem kellene legyőzni a töltések miatti taszító erőt! Itt lép be a gyenge kölcsönhatás, amely negyedóránként alakítja át a neutront protonná és így a tiszta neutronból felépülő tömbök nem stabilak. A neutront és protont is tartalmazó atommagokban a gyenge-kölcsönhatás már nem végzi el az átalakítást, mert a protonok számának növekedése egyrészt erősebb taszítást okoz, másrészt a proton is magasabb energiájú pályára kerülhet. A legstabilabb, azaz a legnagyobb kötési energiával rendelkező atommagokban, ilyen a hélium a neutronok és protonok, egyaránt betöltött pályán helyezkednek el. Ha az atommagban a nukleonok száma n, akkor közöttük n(n-1)/2 pár alakul ki, amivel arányosan növekszik az erős kölcsönhatás hozadéka. Ezért lesz a kötési energia egyre nagyobb az ⁵⁶Fe izotópig bezárólag. Ha ennél is nagyobb a nukleonok száma, akkor már gyarapszik az olyan „távoli” párok száma, amelyek között nincs erős-kölcsönhatás, és ráadásul a nagyobb protonszám növeli az elektrosztatikus taszítást, hiszen ez a kölcsönhatás alig csökken a nukleonok közötti távolsággal. Emiatt válnak bomlékonnyá az olyan atommagok, ahol a protonok száma már közelít százhoz.

A neutroncsillagok fizikája

A neutroncsillagokban már egy új játékos ül le az asztalhoz: a gravitációs kölcsönhatás. Ennek ereje már eléri az erős kölcsönhatás szintjét, de „jobb lapokkal” rendelkezik, mert a kölcsönhatás nincs korlátozva az objektum méretével, ezért képes bármennyi neutron összetartására. De ne felejtkezzünk el a gyenge kölcsönhatásról, amelyik a neutron állományt fokozatosan protonná alakíthatja át, és ha túl sok a proton, az elektrosztatikus taszítás megakadályozhatja a neutroncsillag gyarapodását. Ez magyarázhatja, hogy a tömegük nem haladja meg a Nap háromszorosát.

Szupernóva robbanás

 A neutroncsillagok felfedezése 1935-ben James Chadwick (angol csillagász, 1891-1974, Nobel díj: 1935) nevéhez fűződik, aki a szupernóvák robbanását vizsgálta. A robbanás feltételét Subrahmanyan Chandrasekhar (1910-1995, Nobel díj: 1983) indiai csillagász adta meg, mely szerint ehhez akkora csillag kell, melynek tömege legalább nyolcszorosa a Napnak.  Amíg a csillagban elegendő a hélium termelő üzemanyag a fúzióhoz, addig a sugárnyomás megóvja a csillagot az összeroppanástól, de amikor ez kezd kifogyni a csillag összeroskad és hatalmas energia kibocsátás után csak egy viszonylag kis mag marad vissza, ami lehet egy fehér-törpe, vagy egy neutroncsillag. Ez a robbanás nem szállítja el az óriáscsillag eredeti forgásához tartozó impulzusnyomatékot, viszont a tömeg és még inkább a sugár sok nagyságrenddel lecsökken, amiért a forgást akadályozó tehetetlenségi nyomaték sok nagyságrenddel kisebb lesz, felgyorsítva a forgási frekvenciát akár 10 nagyságrenddel is. A neutronok rendelkeznek mágneses momentummal is, mert az alkotó kvarkok töltés súlypontja nem esik egybe. Így a másodpercenként akár több százszor megperdülő csillag mágneses mezője szétküldi az energiát a lágy rádiósugaraktól kezdve a kemény gamma-sugarakig, létrehozva a pulzárokat.

Mi lehet a fekete lyukak anyaga?

A fekete lyukakról csak keveset tudhatunk, mert egyedül azáltal vehetjük észre jelenlétüket, hogy eltakarják a mögöttük lévő csillagokat. Tömegükre is tehetünk becsléseket a csillagok mozgását tanulmányozva, amit befolyásol a fekete lyuk tömege is. Ezek jellemző tömege a neutroncsillagoknál hozzávetőleg egy nagyságrenddel nagyobb, de a galaxisok centrumában létező óriási fekete lyukak ezt a méretet is sokszorosan meghaladják. A Napnál tízszer nagyobb tömegű objektumokban a kötött fotonok pályasugara már 25 kilométer fölé nő, elérve a fekete lyukak kiterjedését, ha ezek sűrűsége a neutroncsillagokéval egyezik meg. Nem kell tehát a fekete lyukak sűrűségének meghaladni a neutroncsillagét ahhoz, hogy képesek legyenek visszatartani saját sugárzásukat. Kérdés azonban, hogy miért lehet tömegük jóval nagyobb, mint a neutroncsillagoké? Ez úgy képzelhető el, hogy itt nemcsak a neutronok, hanem a protonok, sőt az elektronok is csapdázódnak. A hatalmas gravitációs erő az elektronokat olyan pályára kényszerítheti, ahol a protonok belsejében nagy az elektronsűrűség. Nagy tömegű radioaktív atomokban ismert a K-befogás jelensége. Ez azt jelenti, hogy a legbelső pálya elektronja befogódik, és egy proton neutronná alakul át. Ez a folyamat épp fordítottja a béta-bomlásnak. A fekete lyukban a protonok belsejében lévő nagy elektronsűrűség miatt a K-befogás valószínűsége is megnövekszik, kompenzálva a béta-bomlást, és elősegítve, hogy a fekete lyukak tömege jóval nagyobb lehessen a neutroncsillagoknál.

Mekkora lehet a fekete lyukak sűrűsége?

Lehet-e a fekete lyuk tömegsűrűsége nagyobb, mint a neutroncsillagoké? A válasz nem az erős gravitáció koncepciója szerint, mert ennek F_sgr = ℏc/r² erősségét a tér maximális görbülete határozza meg, ami akkor jön létre, ha a fénysebességű forgások olyan geometriájú részecskéket hoznak létre, ahol a felület nullára zsugorodik a Lorentz kontrakció miatt. Ennél nagyobb torzulás már nem képzelhető el, ezért a sűrűség sem haladhatja meg a nukleonokét. De ne legyünk telhetetlenek, hiszen elegendő lenne a parányi kávéskanalat megtölteni evvel az anyaggal, hogy a Gizai piramis tömegének ezerszereséhez jussunk!

A blog további írásaira a "Paradigmaváltás a fizikában” című bejegyzés hívja fel a figyelmet a megfelelő linkek megadásával.

Fontos epizódok a gondolkodás és a fogalmak fejlődéstörténetéből

Bérczi Szaniszló, ny. egy. docens, ELTE TTK Fizika Intézet, Anyagfizika Tanszék.

Nem is gondoljuk, milyen fontos nyomokat őriz a gondolkodás fejlődéstörténetéről a magyar nyelv. A magyar beszéd és gondolkodás rendszerelemzését egy fizikus végezte el, Bérczi Szaniszló. A szerző azt, hogyan lehet rendszereket áttekinteni a fölbontás és a visszaépítés (szétszedem-összerakom) elv alapján, már sok más tudományágban bemutatta, melyek közül néhány az irodalomban megadott [1], [2], és [3] ponton érhető el.

Legutóbbi összefoglaló cikkében, amely egy 2016-os előadásának nyomtatásban is megjelent változata [4], a gondolkodás és a beszéd őskori fejlődésének fontos mozzanatait az indukciós elv korai alkalmazásaként is bemutatja.

Az „Emlékek a gondolkodás fejlődésének néhány korai lépéséről a magyar nyelvben” (Reminescences of the early steps of evolution of thinking in the Hungarian language) c. cikk

https://www.researchgate.net/publication/312027126_Emlekek_a_gondolkodas_fejlodesenek_nehany_korai_lepeserol_a_magyar_nyelvben_Reminescences_of_the_early_steps_of_evolution_of_thinking_in_the_Hungarian_language?ev=prf_pub

E cikk lényege, hogy korai fogalmaink egyrészt az ősfizika gondolkodási stratégiáját mutatják be, másrészt az alkalmazott nyelvrendszertan föltárja a magyar nyelv ősi „nyelvkémiai” szerkezetét is. Ez utóbbi írása az I. Czuczor-Fogarasi Konferencián elhangzott előadásának írott változata és az Életünk hasábjain jelent meg [5]. Több e témában írott közlemény és füzet is elérhető erről az igen érdekes, a fogalomfejlődést föltáró témáról [6], [7], [8], és [9].

Irodalom:

[1] Acta Geologica Hungarica, 1980/1-4,

https://www.researchgate.net/publication/313220349_Cyclicity_in_the_Evolution_of_Matter_and_its_Application_to_the_Evolution_of_the_Solar_System

[2] Symmetry: Culture and Science, 2016, 27/1.

https://www.researchgate.net/publication/301363897_STRUCTURAL_HIERARCHY_Teaching_sciences_more_effectively

[3] Fizikai Szemle, 2017/1, 32-36. old.  

https://www.researchgate.net/publication/313036968_A_szerkezeti_hierarchia_es_a_folepites-lebontas_szetszedem-osszerakom_elv_The_structural_hierarchy_and_the_construction-decomposition_assembling-disassembling_principle

 [4] Emlékek a gondolkodás fejlődésének néhány korai lépéséről a magyar nyelvben. http://www.egipatrona.hu/mvsz/doc/Nemzetstrategiai%20berczi_175_214.pdf

[5] Életünk, 2011/3-4, 38-55. old.

Bérczi Sz. (2011): Magyar nyelvkémia. Életünk, 2011/3-4. szám. 38-55. old

https://library.hungaricana.hu/hu/view/Eletunk_2011/?pg=239&layout=s

[6] Bérczi Sz. (2013): Égberagadás, földreszállás az ősi eurázsiai díszítőművészetben, kitekintéssel a nyelvfejlődéstörténetre. Eurázsiai művészetek 28. TKTE, 52. old. Pirehab, Debrecen (ISBN 978-615-5412-00-4) http://www.federatio.org/tkte/Egberagadas.pdf

[7] Bérczi Sz. (2014): A fogalomfejlesztés művészete a Kárpát-medencében és Eurázsiában. Eurázsiai művészetek 29. TKTE, 56. old. Pirehab, Debrecen. (ISBN 978-615-5412-01-1) http://www.federatio.org/tkte/Fogalomfejlesztes.pdf

[8] Bérczi Sz. (2015): A gondolkodásművészet kifejlődése a Kárpát-medencében és Eurázsiában. Eurázsiai művészetek 30. TKTE, 52. old. Pirehab, Debrecen  (ISBN 978-615-5412-03-5)

[9] Bérczi Sz. (2016): A gondolkodás és a beszéd művészetének felvirágzása a korai időkben a Kárpát-medencében és Eurázsiában. Eurázsiai művészetek 31. TKTE, 52. old. Pirehab, Debrecen (ISBN 978-615-5412-04-2)

A blog további írásainak összefoglalása a linkekkel együtt elérhető a „Paradigmaváltás a fizikában” című bejegyzésben.