A szeptember 12.-én az OZON TV "Egyenlítő" című műsorában elhangzott riport elérhető:

https://ozonetv.hu/teljes-adasok/2020/09/17/big-bounce-elmelet/489?fbclid=IwAR0_SP7mSk34dzFkxZoE0hC_iPMgxVp0v2qxYpkj00m6l-opGcEFSzh7_ew

A blog további írásai: "Paradigmaváltás a fizikában"

Az utóbbi másfél évben új frontvonal jött étre a kozmológiai elméletek növekvő táborában.  A jelenleg uralkodó ősrobbanás elmélet kulcsmotívuma az univerzum inflációja, amely az elképzelések szerint a semmiből való keletkezés első másodpercének parányi része alatt megy végbe. Ennek helyébe javasol egy új elképzelést a Nagy Felpattanás számítógépes szimuláción alapuló koncepciója (angol nyelven az előbbi a Big Bang, az utóbbi a Big Bounce elnevezést kapta). Az új elmélet egyik frontharcosa Ijjas Anna a Max Planck Intézetből, legfőbb támogatója pedig a „renegát”, Paul Steinhardt a Princeton University-ből, aki korábban az inflációs elmélet egyik kidolgozója volt, most pedig annak egyik legfőbb kritikusa lett. A kritikát úgy fogalmazza meg, hogy amíg az infláció elmélete minden kérdésre választ ígér, valójában egyetlen kérdésben sem ad igazi választ. A gond abból fakad, hogy az ősrobbanás utáni világ legtöbb tartományában nem áll le az infláció helyet adva az univerzum jelenleg megfigyelt – a fénysebességnél lassabb – tágulásának. A következmény emiatt, hogy végtelen számú párhuzamos és egymástól elszigetelt univerzum alakul ki, melyek közül csak az egyik a miénk, ahol létezünk. Ez a multiverzum vitatott – hiszen semmi módon nem ellenőrizhető – koncepciója.

De nézzük először, hogy miért is volt szükség az ősrobbanás elméletben a rejtélyes inflációs szakaszra, amikor az univerzum mérete a másodperc tört része alatt – a fénysebességet messze meghaladó sebességgel – korábbi méretének sokszorosára fújódott fel? A hipotézis oka, hogy magyarázatot keresünk az univerzum galaxisainak eloszlására, amely nagy távlatokban nézve minden irányban azonos (azaz izotrop) és a távolságtól függetlenül mindenütt egyenletes sűrűségű (tehát homogén). Ha egyetlen nagy robbanás hozta létre az univerzumot, akkor ez a szabályosság rendkívül valószínűtlen, kellett ezért egy magyarázó mechanizmus, ez lett a már említett infláció. Ennek folyamán a kezdeti gravitációs egyenetlenségek kisimulnak, előáll a mai is érvényes homogén és izotrop univerzumunk. Szintén ez a folyamat vezet el a gravitációs mező „lapos” szerkezetéhez. Ez alatt azt kell érteni, hogy a kezdeti óriási tömegsűrűséghez a relativitáselmélet vadul változó térgörbületet rendel, ami nagyon távol lehetett a mai közel euklideszi szerkezettől, de a hatalmasra tágult méretek miatt a görbületi ráncok kisimultak, és létrejött mai univerzumunk sima, és laposnak nevezett geometriája.

Univerzumunk homogén szerkezetét így tehát ki lehetett békíteni az ősrobbanás elméletével, de bőven maradtak azért kifogások is. Mindenekelőtt nem sikerült meggyőző magyarázatot adni arra, hogy mégis milyen erő hozza létre ezt az inflációt és mi okozza a folyamat leállását, és ott van még, a már említett multiverzum ellenőrizhetetlen koncepciója is. A kifogások háttérbe szorultak a minden irányból egyenletesen érkező mikrohullámú háttérsugárzás megfigyelése miatt, és jelenleg a kozmológusok nagy többsége elfogadja az inflációs modellt.

Amióta Hubble megfigyelése alapján kialakult az ősrobbanás elmélete, mindig is voltak párhuzamos elképzelések, amelyek a semmiből előpattanó egyetlen nagy robbanás helyett váltakozó tágulási és összehúzódási fázisokban gondolkoztak, ez a pulzáló, vagy oszcilláló kozmológia. Ugyancsak próbára teszi a fantáziát elképzelni, hogy a gombostű fejénél sokkal kisebb pontba hogyan lehet összetömöríteni, akár csak saját Földünk egész tömegét, nemhogy még a Nap, sőt Tejutunk százmilliárd csillagát, sőt még az univerzum milliárdnyi galaxisát is! Ha az univerzum pulzál, akkor nem kell, hogy eljusson ennyire szélsőséges viszonyok közé, ekkor tágulási és összehúzódási folyamatok egymásután jönnek létre. Ez az univerzum mindig is volt, és mindig is lesz, elkerülve a kényes kérdést: hogyan lehet a semmiből valami. Mi is bemutattunk egy ilyen alternatív elképzelést a qubitban: „Ha nem fogadjuk el az ősrobbanás elméletét, még mindig van egy másik”. Itt arra mutattunk rá, hogy a távolabbi galaxisokból érkező fény vöröseltolódása nem csak a galaxisok távolodásával magyarázható, hanem avval is, hogy a távoli múltban nagyobb volt a fénysebesség, és ezt összekötöttük a sötét energia és a sötét anyag arányának változásával is, amit az E = mc² összefüggés alapján a c értéke határoz meg. Ha nagy c értéke, túlnyomó lesz a sötét energia, ha kicsi, akkor a sötét anyag dominál. A sötét energia eltávolítja egymástól a galaxisokat, a gravitáció összehúzza. Ezért az ősi univerzumban – bár kisebb mértékben, de jelenleg is – a taszítási erő dominál, de lehetett egy még ősibb korábbi állapot, amikor összehúzódott az univerzum, és lehet olyan is a távoli jövőben, úgy egy billió év múlva, amikor elkezdődik egy újabb összehúzódási szakasz.

Ijjas Anna számítógépes szimulációi is pulzáló univerzumra vezettek. A számítások az általános relativitáselmélet gravitációs egyenletéből indultak ki. Erről az egyenletről azt kell tudni, hogy az energiát és az impulzust négydimenziós tenzorok adják meg, amelyeket a tér három és az idő koordinátáinak segítségével építünk fel. Ezek a tenzorok a tér görbületi szerkezetétől (metrikájától) függenek. Ha ismert a metrika, akkor nincs gond, megfelelő számítógépes technikák segítségével az egyenlet megoldható. A nehézséget az jelenti, hogy először ismerni kellene a metrikát, amikor nekifogunk a megoldásnak. Jelenlegi „lapos” univerzumunkban ez megoldható, mert kicsi az euklideszi geometriától való eltérés, de az univerzum korai fázisában már a számítás sokszor önkényes megoldásokat eredményez: ha más a kiindulási metrika, akkor más lesz az eredmény is. A lehetséges megoldásokat két fő paraméterrel lehet jellemezni, az egyik a skála faktor, ami az univerzum méretét adja meg, a másik a kozmikus látóhatár sugara (ezt az Einstein által bevezetett taszító jellegű sötét energia, vagy más néven a kozmikus állandó, határozza meg). Az inflációs számításokban ez a sugár lényegében állandó, de épp ezt vette górcső alá Illyés elgondolása. Ugyanis erősen torzult metrikák esetén ez a látóhatár nagyon kicsi lehet. Szemléletesen ezt egy ballonon lévő hangyával mutathatjuk be. Ha parányi a ballon, akkor a nagy görbület miatt a látóhatár leszűkül, felfújva a ballont a terep kisimul és messzire távolodik a látóhatár. Erre alapozva történt a szimulációk hosszú sora, ahol akár a legvadabb geometriákból is kiindulva olyan megoldásokat kaptak a látóhatár megnövekedése miatt, amelyben a kezdetben erősen csavart, nagy ráncokkal szabdalt térgeometria, az univerzum lassú összehúzódása során homogén, izotrop és lapos szerkezetbe ment át. Következtetésük: nem csak az inflációs tágulás magyarázhatja a homogén univerzumot, hanem a lassú összehúzódás is.  

Az ősrobbanás híveit a számítások nem győzték meg,  fölvetik az entrópia kérdését is, a végtelenszer ismétlődő tágulási és összehúzódási ciklus végtelenre növelné az entrópiát. Kitartva korábbi felfogásuk mellett, nagy önbizalommal jelentik ki, hogy nem tartják igazi versenytársnak az új elméletet sem.

Ijjas és munkatársai elméletük továbbfejlesztésén gondolkoznak, akár Einstein egyenletének bővítését is lehetségesnek tarják, hiszen nincs rá garancia, hogy ez már a végső formalizmus lenne. Erre utal az is, hogy még Einstein is tévedésnek nyilvánította az univerzum gravitációs egyensúlyát biztosító kozmikus állandó bevezetését, amikor hírül kapta, hogy az univerzum tágul Hubble megfigyelése alapján. Ez a tag mégis visszakerült az egyenletbe, mert kiderült, hogy a tágulás sebessége növekvőben van.

 A vita még biztosan tovább fog tartani, mert nehéz igazságot tenni, hogy mi történt a mikrohullámú sugárzás kialakulása előtt úgy 13,4 milliárd éve. Ekkor az óriási anyag és energiasűrűség rendkívül magas hőmérséklettel járt együtt, szétvetve az atomokat is. A kaotikusan kavargó pozitív és negatív töltések pedig elnyeltek minden fényt. Ez volt az univerzum sötét korszaka. Ennek függönye nem teszi lehetővé, hogy bármikor beláthassunk a sötét korszakot megelőző univerzum világába, és ez törölheti a korábbi ciklusok entrópiáját is.

A témáról az OZON TV „Egyenlítő” című műsorában készült a szerzővel interjú, ami szeptember 16.-i kerül adásba.

Az anyag megjelent kisebb változtatásokkal a qubit portálján „A Big Bounce lenne az Új Big Bang?” címmel.

Link a blog további írásaira: „Paradigmaváltás a fizikában”

Útikalauz a fizikához Newtontól Higgsig

Kaslik Gyula: Szindbáddal a negyedik dimenzióban

A tervek szerint a Scolar kiadásában jelenik meg a könyv a karácsonyi könyvvásárra. Előzetesen az előszót és a tartalomjegyzéket mutatja be a blog.

Előszó

Különleges útikalauzt kínálunk az olvasónak, aki szeretné bejárni a fizika megismerésének zegzugos útjait. Először tegyünk sétát a hétköznapi világban, hogy megismerkedjünk néhány alapvető fizikai fogalommal, majd ennek birtokában merészkedjünk nagyobb utakra. Ennek során látogatást teszünk a Föld belsejébe, majd szakadjunk el a Földtől, hogy látogatást tegyünk a csillagok világába is. Merüljünk el a messze múltba, az univerzum kezdeteihez is, vessük fel a nagy kérdést: honnan származik univerzumunk? Az útikalauznak ez a része még ismeretterjesztő jellegű és főleg kezdő utazóknak szól, de gyakorlottabb utazók számára kínál kalandot, amikor bejárjuk a parányok világát, és az anyag legkisebb építőköveit akarjuk megismerni. Itt már sok nehézséget jelent, hogy ennek törvényei már annyira mások, és ezek megértését nehezíti, hogy itt az útjelzőt bonyolult matematika képletek adják meg nekünk. Ezt akarja megkönnyíteni a könyv, amikor olyan utat próbál találni, amely bemutatja, hogyan juthatunk el az egyenletekhez néhány egyszerű elv megfogalmazásával. Ilyen elv a részecskék fénysebességű forgásokkal való azonosítása is. Ennek során kiderül, hogy ha jól megértjük az alapelveket, akár már egyenletek nélkül is eligazodhatunk ebben a világban.

A fizika nagy felfedezői Newtontól Higgsig adják meg a segítséget utunk során, alkotásuk mára az emberiség kulturális öröksége lett. Ez ugyanakkora kincs, mint amit a képzőművészet, az irodalom, a zene és az építészet nagyjai hagytak ránk. Becsüljük meg ezt az örökséget! Ez az örökség azonban nem múzeumi tárgy, vegyük bátran a kezünkbe és próbálkozzunk vele akárcsak a lego játék elemeivel. Próbáljuk meg másképp is összerakni, ha ez sikerül sok meglepetésben lehet részünk. Az se baj, ha nem sikerül, abból is tanulhatunk, mert így értjük meg jobban a működését. A nagy elődökhöz nem akkor vagyunk hűek, ha szavaikat ismételgetjük, hanem akkor, ha használjuk gondolataikat és annak segítségével keresünk új utakat. De legyünk tisztában vele, hogy nem csak egyetlen út van, amin tovább haladhatunk, vállaljuk bátran a tévedés kockázatát is. A fizika attól lesz élő tudomány, ha különböző nézetek csapnak össze. Erre törekszik a könyv is, amiben szerzőtársam Kaslik Gyula fog segíteni, amikor egy olyan útra csábítja az olvasót, amely már kivezet a tér szokásos három dimenziójából is. Kaslik nézetei részben kiegészítik az első négy fejezetet, részben más irányba visznek. Emiatt a két szerző véleménye sem minden kérdésben azonos, viszont abban egyezik törekvésük, hogy a világ megértéséhez utat találjanak.

Könyvünk szervesen kapcsolódik a Scolar kiadásában 2017-ben megjelent műhöz: Rockenbauer Antal: „A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója”. Az ismétlés elkerülésére törekszünk, de ahol a könnyebb olvashatóság megkívánja, egyes gondolatok, matematikai formulák újra elő fognak jönni. Másutt viszont, ahol a fő gondolatmenet megértését nem nehezíti meg, csak hivatkozások szerepelnek a korábbi könyvre.

 Tartalom

I. Bevezetés

I.1. Elvek és egyenletek

I.2. Mechanikai alapfogalmak: energia, impulzus, erő és tömeg

II. Utazások a Földön és a csillagok világában

    II.1.. Miért jobb Moszkvába repülni, mint Párizsba?

    II.2. Súlytalanság a Föld középpontjában?

    II.3. Megvalósulhat-e valaha a csillagközi utazás?

    II.4. Ikerparadoxon: a látszat valósága

    II.5. Hogyan jönnek létre a fekete lyukak?

    II:6. Hogyan változott az univerzum az ősrobbanástól napjainkig? Óriások a házban

III. Utazás a mikrovilág útvesztőiben

    III.1. Démokritosz és a kvantumfizika

    III.2. A koldus és királyfi

    III.3. Elektronok tánca és a kémiai kötés

    III.4. Visszafordítható-e az idő iránya a kvantumok világában?

    III.5. Nobel-díjas doktori disszertáció: de Broglie felismeri az anyag hullámtermészetét

    IV.. A fénysebességű forgás koncepciója

          IV.1. Lehet-e pontszerű az elektron?

         IV.2. Folytonosság, pontszerűség és diszkrét energiák

         IV.3. A részecskék tömegének és impulzusnyomatékának eredete

         IV.4. Kettősforgás és a spin

         IV.5. A részecskét stabilizáló erős gravitáció

         IV.6.  Az elektromos töltés eredete

         IV.7. A kettős térforgások gravitációs mezője

        IV.8. Miért végtelen az elektron sajátenergiája a QED elméletben?

        IV.9. Fizikai alternatívák és matematikai fetisizmus

       IV.10. Pillantás az elemi részecskék belsejébe: az erős kölcsönhatás

       IV.11. Látogatás a részecskék szerelőműhelyében: a gyenge kölcsönhatás

       IV.12. Higgs elméletéből eredeztethető a fénysebességű forgások koncepciója

       IV.13. Úton a kölcsönhatások egyesített mezőelmélete felé

       IV.14. A fénysebességű forgás elve mint szemléleti módszer

V. Kaslik Gyula: Szindbáddal a negyedik dimenzióban

Előszó

V.1. Bevezetés

V.2. Előhang: a fázishatáron

V.3 .A határtér, avagy a gumiszőnyeg, a korongbolygó és Mézga Aladár

V.4. Szimmetria. Szindbád a tükör misztikus világá5.A kölcsönhatások egységes birodalma. Fénysebességű forgások a határtérben

V..5. A 4 térdimenziós téregyenletek és a kvantum-elektrodinamika találkozása

V.6. Összefoglalás

V.7.  Szindbád utószava

A blog további írásai elérhetők: „Paradigmaváltás a fizikában”

Hogyan vezet el a relativisztikus energiaegyenlet a Higgs bozon koncepcióhoz

Pozitív-negatív, jó-rossz, hideg-meleg, múlt-jövő, jobbra-balra és még sokáig sorolhatnánk az ellentétpárokat: gondolkozásunk egyik alapköve az alternatívák, ellentétpárok szembe állítása. A fizikai fogalmak világában is kulcsszerepet játszanak a kétértékű mennyiségek, amelyeket valamilyen szimmetria köt össze, és amelyek tulajdonságait matematikai összefüggések által adjuk meg. Ezek tovább lendítik megértésünket a fizikai valóságról, de gyakran csapdába esünk, ha már jobban hiszünk egyenleteinknek, mint annak a valóságnak, mint amiből egyenleteink származnak. Ezt a felfogást nevezném matematikai fetisizmusnak. Először egy ilyen példából indulunk ki, majd nekifogunk, hogy bemutassuk az elemi részecskék világának legfontosabb alternatíváit, és kísérletet teszünk arra, hogy a Higgs bozont is beillesszük a fénysebességű forgások közé.

Honnan ered a lyukelmélet?

A matematikai fetisizmus egyik legismertebb példája a lyukelmélet. Ennek megértéséhez a relativitáselméletből kell kiindulni, amelyik már önmagában is sok félre- és belemagyarázás kiindulópontja. A klasszikus mechanika alapjait Newton fektette le, kimondta az erő és a gyorsulás arányosságát, amit a tehetetlen tömeg kapcsol össze, és megfogalmazta az energia megmaradás tételét, amely a mozgási és potenciális energia összegének állandóságát mondja ki. A törvények matematikai alakja jól írja le a kis sebességek világát, de már korrekcióra szorul nagy sebességek esetén, amikor beleütközünk egy felső korlátba, amit az átléphetetlen fénysebesség szab meg. A mechanika relativisztikus szabályait az elektrodinamika Maxwell egyenletei alapozzák meg, amely elvezetett a mozgási energia fogalmának továbbfejlesztésére is. A klasszikus mechanika az E_Kin =  ½mv² összefüggésből definiálja a kinetikus energiát, ezt váltja fel a kovariancia törvény

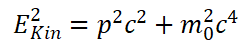
Ez a törvény kis sebességeknél, azaz amikor a p·c impulzus tag kicsi az m₀c² nyugalmi energiához képest, reprodukálja a szokásos kinetikus energiát, ha alkalmazzuk a négyzetgyökvonás sorfejtési szabályát. Az eltérés csak abban jelentkezik, hogy a teljes kinetikus energia tartalmazza a nyugalmi energiát is:

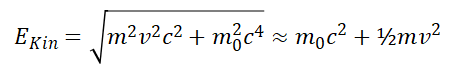
Honnan származik a kovariancia törvény szokatlan négyzetes összeadási szabálya? Ilyen szabály vektorok összeadásánál természetes, de hát miért lenne vektoriális eredetű a nyugalmi energia? Talán mégis valamilyen mozgás bújik meg mögötte? Az összefüggés négyzetes jellege érthető, ha a nyugalmi energia valójában a részecske saját belső forgásának kinetikus energiája, és a külső és belső mozgások impulzusát a vektorok összegzési szabálya szerint adjuk össze, és figyelembe vesszük, hogy a saját forgás gömbszimmetriája miatt nem képződik kereszt tag a kétféle mozgás között.

Problémát jelent, hogy a négyzetgyökvonás két előjelet adó művelet, amiért negatív kinetikus energia és negatív nyugalmi tömeg is származtatható a kovariancia szabályból. De mit lehet kezdeni a negatív értékekkel? A negatív tömeg például azt jelentené, hogy a test a ráható erő irányával ellentétes irányban mozog. Ilyesmit a természetben nem lehetett megfigyelni. Az igazi problémát a relativisztikus kvantummechanika hozta elő, amikor a kovariancia törvénybe bevezették a fizikai mennyiségek operátorait. Mivel a potenciális energia és a kinetikus energia skalárként (lineárisan) és nem vektorként (négyzetesen) adódik össze, így nem kerülhető el a négyzetgyök kibontása, amit Dirac négydimenziós spinorok bevezetésével oldott meg. Az eljárás négykomponensű lineáris differenciál egyenletrendszerre vezetett. A négyzetgyökvonás szabályai miatt a számítások nem csak pozitív, hanem negatív energiájú megoldásokat is adtak. Ekkor következett be az a pont, amit a matematikai fetisizmusnak nevezhetünk: megpróbáltak a negatív energiájú megoldásnak is fizikai értelmet adni. A kvantummechanikában ugyan mindig az energiakülönbségnek van értelme, mert ez határozza meg a kibocsátott, vagy elnyelt fotonok energiáját, így elvben az energia nullapontja tetszőleges lehet. Viszont ennek a negatív energiának nincs alsó határa, ami avval jár együtt, hogy ez elektronnak el kellene tűnnie. Ezt próbálta magyarázni Dirac avval a hipotézissel, mely szerint a tér mindenütt már fel van töltve végtelen számú negatív energiájú elektronnal, és így a valódi elektronok már efölött a „tenger” fölött lebegnek. Az abszurdnak tűnő elmélet megerősítést nyert a pozitron felfedezésével, amelynek tulajdonságai egyeztek az elektronnal, csak a töltése volt pozitív, és elektronnal ütközve a két részecske megsemmisíti egymást gamma-sugarak kibocsátásával. Ez jól beleillett a képbe, mert ha a negatív elektronok tengeréből hiányzik egy részecske, annak tulajdonságai pont megfelelnek a pozitronénak.

Ettől kezdve vált gyakorlattá az elméleti fizikában, hogy a valóságot igyekeztek hozzáigazítani a matematikai egyenletek kívánalmaihoz. Ez az, amit matematikai fetisizmusnak nevezhetünk. A helyes út viszont, hogy ki kell jelölni a matematikai formulák érvényességi határát! Végül is minden egyenlet egy „hasonlat”, amely elősegíti a jelenségek megértését, de a hasonlat nem maga a valóság. Ha az egyenlet – például a kovariancia törvény – különböző megoldásokat, esetünkben negatív energiát is felkínál, akkor azt kell megnézni, hogy találunk-e olyan fizikai jelenséget, amely indokolja, hogy helyesnek fogadjuk el-a negatív értéket. Ha viszont ilyen indokot nem találunk, akkor mondjuk ki, hogy a szóban forgó megoldás hamis.

Az idő irányának megfordíthatatlansága

Nézzük hát a negatív energia kérdését! A probléma gyökerét ott kell keresni, hogy a kvantummechanika egyenletei nem ismerik az idő irányát. A fizikában az entrópia növekedés elve az egyetlen, amely megtiltja a múltba való visszalépést. Ennek lényege, hogy az energiaátalakítási folyamatok mindig veszteséggel járnak, a korábbi állapotba való visszatérés nem lehetséges a képződő hőenergia miatt, ami annak felel meg, hogy az energiakonverzió a magasabban rendezett állapotból kevésbé rendezett állapotot hoz létre. A kovariancia elv sem különbözteti meg az idő irányát, ez bújik meg a negatív energia jelentkezésében is. Az energia és az idő a kvantummechanikai felfogás szerint egymás „ikertestvére”: az energia operátora az idő függvényében képzett differenciálhányadossal arányos, és emiatt az idő irányának megfordítása magával hozza az energia előjelének megfordulását. Az idő irányának megfordíthatatlansága miatt a Dirac egyenlet matematikai megoldásából kapott negatív energiájú állapotok tehát a valóságban nem léteznek, ezeket a fizikai valóság szempontjából hamis megoldásának kell tekinteni, és nem kell attól tartani, hogy az elektron „leesik” a negatív végtelen energia állapotába.

A királis szimmetria szerepe a részecskefizikában

A fénysebességű forgások koncepciója az elektron-pozitron kettősségre egyszerű magyarázatot ad: mindkét részecskét kéttengelyű forgások alkotják, melyek királis szimmetriája fordított, az egyiknek jobbkéz, a másiknak balkéz szimmetria felel meg a két forgás eltérő sodrásiránya miatt.

 Ehhez kapcsolódik egyrészt a töltések ellenkező előjele, másrészt a két részecske egymást megsemmisítő reakciója is: a kettős forgások egyike az ellentétes forgásirány miatt megsemmisül, a másik viszont megmarad, hiszen azonos a forgásirányuk, ez a megmaradó egytengelyű forgás pedig a képződő gammasugárzás fotonja.

Lehet-e negatív a tömeg?

A kovariancia elv négyzetes felépítéséből további következtetések is levonhatók. Nézzük először a tömeg kérdését! Mind a nyugalmi energia, mind az impulzus a négyzeten szerepel. Ez alapján a tömeg is lehetne negatív! Ez látszólag ellentmond korábbi állításunknak az E = mc² ekvivalencia szabály miatt. Viszont a kovariancia elvvel adekvát összefüggés

E² = m²c⁴

formában adható meg. Ha így fogalmazzuk meg a tömeg és energia ekvivalenciáját, akkor már szabad az út a negatív tömeg felé! Milyen fizikai folyamat indokolja, hogy beszéljünk negatív tömegről? Hát az anyag és antianyag kettőssége! Ezt úgy fogalmazzuk meg, ha a pozitív tömegű elektron találkozik a negatív tömegű pozitronnal, akkor a két tömeg megsemmisülése idézi elő az annihilációt! Ez eddig csak az annihilációs folyamat újfajta értelmezése, de a negatív tömegnek van ennél sokkal fontosabb megjelenése is, mert képes magyarázatot adni a neutrínó rejtélyre és kulcsot ad a kvarkok különös tulajdonságainak megértéséhez is.. A neutrínó rejtély abból fakad, hogy a mérési pontosság határain belül a neutrínó mindig fénysebességgel halad, ami csak nulla nyugalmi tömegű objektum – ilyen a foton – esetén lehetséges. Viszont a neutrínó oszcilláció jelensége szerint létezni kell három különböző neutrínónak. Mivel a neutrínónak nincs töltése és a spinje ½, akkor mi lehet közöttük a különbség, ha még a tömeg is egyezik (azaz nulla)? A választ a kvantummechanika szuperpozíciós elve és a negatív tömeg fogalmának bevezetése adja meg. A szuperpozíció elve azt jelenti, ha két állapotot valamilyen szimmetria köt össze és azonos energia tartozik hozzájuk, akkor a két állapot szuperpozíciója is érvényes állapotfüggvény. Fogjuk úgy fel a neutrínót, mint olyan szimmetrikus állapotok szuperpozícióját, amelyben az egyikhez pozitív, a másikhoz negatív tömeg tartozik, és a szuperpozíciós súlyfaktor azonos. Az ilyen állapotban már nulla lesz a tömeg, és emiatt nincs akadálya, hogy a neutrínó fénysebességgel haladjon. Ugyanakkor az egymást kiegyenlítő +m és –m tömegek más-más értéket vesznek fel a neutrínók három típusában.

 Az anyag jellegű részecske (például elektron) antianyag párja (pozitron) abban is különbözik, hogy fordított elektromos töltésük előjele. Például az elektron töltése –e, a pozitroné pedig +e. A neutrínót alkotó szuperpozíciós állapotban az egyenlő súlyfaktorok miatt a két töltés kompenzálja egymást, és ezért a részecske elektromosan semleges lesz.

A spin megjelenése a relativisztikus kvantummechanikában

Vizsgáljuk meg a kérdést, hogyan került be a spin fogalma a Dirac formalizmusba? Ez is a kovariancia elv négyzetes jellegére vezethető vissza. A Dirac egyenlet az elektron elektromágneses kölcsönhatásait írja le. A potenciális energiának két tagja van, az egyik a Փ(r) skaláris potenciál, a másik az A(r) vektorpotenciál.  (Itt és a továbbiakban a vastagon szedett szimbólumok jelölik a vektorokat). Az előbbiből származik az elektromos mező a grad, az utóbbiból a mágneses mező a rot vektor algebrai műveletei által. A potenciálokat az elektromos töltéssel szorozva kapjuk meg az elektromágneses energiát. Mivel az elektromos mező a statikus töltésekből, a mágneses mező a mozgó töltésektől (áram) származik, így a relativisztikus energiához való hozzájárulások eltérő: az elektromos mező potenciális energiája lineárisan adódik hozzá a kinetikus energiához, viszont a mágneses energia közvetlenül az impulzust egészíti ki, hiszen mindkét mennyiség a sebességgel arányos. A Dirac elektron energiája elektromágneses térben:

A négyzetgyök felbontása spinorokkal

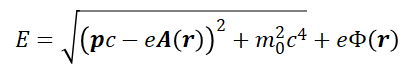
A fenti kifejezésben a töltést és a tömeget még konstansok képviselik. A négyzetgyökvonást a mátrixtechnikával bonthatjuk fel négydimenziós spinorok bevezetésével. Nézzük meg a spinor felbontás alapelvét, amikor egy háromdimenziós a vektor és egy skaláris  b mennyiség négyzetösszegét úgy visszük ki a négyzetgyök alól, hogy abban a vektoriális a és a skaláris b tagok lineáris összege szerepeljen, és az  együtthatókat a négydimenziós spinor elemei adják meg:

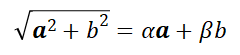
A felbontás megköveteli, hogy a vektoriális α és a skaláris β spinor mátrixok négyzete egységmátrixot alkosson, a komponensek szorzata pedig legyen antiszimmetrikus.  A szóban forgó spinorok felépítése visszavezethető 2x2 dimenziós Pauli mátrixokból képzett blokkokra:

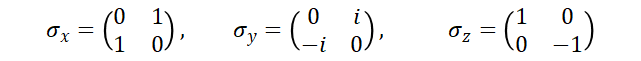
Ezekre a Pauli mátrixokra is teljesül, hogy négyzetük az egységmátrix és szorzatuk antiszimmetrikus (azaz xy + yx = 0). Az elektronspin vektorát a Pauli mátrixokkal lehet definiálni: S = ½σ.  A Dirac által alkalmazott spinoros felbontás egyetlen tagként kezeli az impulzusból és a mágneses mezőtől származó tagot. Az utóbbiban a vektoralgebrai művelet elvégzése adja ki a Zeeman energiát:

E_Zeeman = μ_Bσ·B = 2μ_BS·B

ahol μ_B = eħ/2mc a Bohr magneton és B a mágneses mező vektora. A szokásos konvenció szerint a B mező irányában vesszük fel a z tengelyt, ezért

E_Zeeman = μ_Bσ_zB = 2μ_BS_zB

Itt B jelöli a B vektor abszolút értékét. Mondanivalónk szempontjából annak van jelentősége, hogy a kovariancia elvből következik az a kétértékűség, ami a mágneses mezőben felvett energia pozitív vagy negatív előjelében mutatkozik meg. Szemléletesen ez a kettősség annak felel meg, hogy az elektron a mágneses mező körül két sodrásirányban végezhet forgásokat: jobbra és balra, és az egyik energianövekedéssel, a másik csökkenéssel jár együtt.

A töltés- és tömegoperátorok bevezetése

Terjesszük ki a kvantummechanika szokásos formalizmusát, amely csak az energiát, impulzust és impulzusnyomatékot írja le operátorokkal, míg a kifejezésekben a tömeg és a töltés konstansként szerepel. Vezessünk be kétdimenziós operatorokat a tömeg és a töltés számára is, amelyeknek két lehetséges sajátértéke van: az egyik pozitív a másik negatív. Ez a töltésoperátor esetén –e és +e, a tömegoperátornál +m és –m. Ez a leírás analóg a spinre (impulzusnyomatékra) érvényes szabállyal, ahol az S_z spinkomponens +½ és -½ értékeket vehet fel.

Lépjünk túl azon a gyakorlaton, amely az impulzushoz kötődő kinetikus energiát és a mágneses kölcsönhatás energiáját egyetlen tagként kezeli a négyzetgyökös kifejezésben. Ez a töltés operátor bevezetésével oldható meg, ami által tetszőleges elemi fermion (elektron, pozitron, neutrínók, kvarkok) leírására alkalmas formalizmushoz jutunk.  Annak mintájára, ahogy a fermionok impulzusnyomatékát a spin z komponensével jellemezzük, azaz S_zħ = ½σ_zħ, vezessük be a töltés és tömeg operátorát a z irányú Pauli mátrix segítségével:

A mátrixok vesszőzése azt fejezi ki, hogy ezek a Pauli mátrixok a kétdimenziós királis térben működnek, és nem a spin forgások terében.  Ennek a kétdimenziós mátrixnak bevezetése avval jár együtt, hogy a spinor felbontásban nyolcdimenziós mátrixok lépnek fel, melyekre szintén érvényes, hogy négyzetük az egységmátrix és szorzatuk antiszimmetrikus.

A relativisztikus kovariancia elv a fizika olyan általános törvénye, amely valamennyi részecskére vonatkozik. Az összefüggés négyzetgyökének 8 dimenziós spinorokkal való felbontása vezet el az elemi részecskék tulajdonságainak meghatározásához. A fénysebességű forgások koncepciója specifikus kettősforgásként értelmezi a fermionokat. Az egyes részecskék sajátságait az határozza meg, hogy mekkora a királis arány. Az elektron és pozitron tiszta királis állapotnak felel meg, szemben a neutrínókkal és kvarkokkal, ahol keveredik a két királis szimmetria, és ezt a keveredést neutrínóknál a gyenge kölcsönhatás, kvarkoknál az erős kölcsönhatás idézi elő. Evvel kiterjesztjük a nukleáris erők szerepét, melyeket olyan mezőnek tekintünk, amely „kiválasztja” a részecskék forgásának szimmetriáját. Értelmezzük a Zeeman kölcsönhatás mintájára a királis térben működő erőket és a hozzá tartozó energiát:

E_gyenge = σ’·F_gyenge és  E_erős = σ’·F_erős

A királis állapotok keveredésének mértékét – azaz a részecske töltését – az határozza meg, hogy az F erő iránya mekkora χ_n szöget alkot a z tengellyel:

E_n = [σ’_xsin(χ_n) + σ’_zcos(χ_n)]F_n

Itt F_n az erő abszolút értéke, míg a különböző fermionokat létrehozó erő irányszöge:

cos²(χ_n) =(n+3)/6

 Az n kvantumszám határozza meg a részecskék alapvető paramétereit.   Az n = 0 kvantumszám esetén a két királis szimmetria egyenlő arányban keveredik, az n = 1 és n = 2 eset felel meg a down illetve up típusú kvarkoknak, míg ha n = 3, akkor kapjuk a tiszta királis állapotot, ez felel meg az elektronnak és a pozitronnak.

Az n kvantumszám által meghatározott töltésmátrix diagonális elemei adják meg az elemi fermionok töltését. A spinek analógiájára bevezetett kétértékűség a töltésen kívül a tömegre is vonatkozik. Neutrínó állapotban a töltés és a tömeg egyaránt nulla, mert a két operátornak nullák a diagonális elemei. Ez teszi lehetővé, hogy a neutrínók fénysebességgel haladjanak. A két kvark típus esetén a töltés és tömegoperátornak egyaránt vannak diagonális és nem diagonális elemei. A diagonális elemek adják ki a ±2/3e és ±1/3e töltéseket. Mivel a tömeg operátor sem diagonális, így a kvarkokhoz nem tudunk valódi tömeget rendelni és a Standard Modell csak renormált tömegekről beszél. A kvark állapotok létrejöttéhez szükség van az erős kölcsönhatás jelenlétére, ennek rövid hatótávolsága miatt ez az állapot csak a kvarkokból felépülő hadronok (barionok és mezonok) belsejében van jelen. Ez magyarázza, hogy szabad kvark – azaz tört töltés – nem figyelhető meg. Ugyanúgy evvel lehet magyarázni, hogy csak egész töltésű hadronok, azaz tiszta királis állapotok jöhetnek létre a két, illetve három kvarkból felépülő hadronokban.

Higgs bozon a fénysebességű forgásmodellben

Felmerül a kérdés, hogy a Higgs bozon hogyan illeszthető be az eddig vázolt keretek közé? Ez az egyetlen olyan elemi részecske, amelynek az elmélet szerint nulla a spinje. Ilyen részecske állapot úgy jöhet létre, ha a Higgs mezőnek is van állapot kiválasztó szerepe. Ez a mező azonban nem a királis térben, hanem a spin forgási terében fejheti ki hatását, mégpedig merőlegesen a z irányra:

E_Higgs = σ_x·F_Higgs

Úgy is mondhatjuk, hogy a vessző nélküli Pauli mátrix x komponensével arányos mező váltja ki azt a szimmetriatörést, amely létrehozza a tömeggel rendelkező, de nulla spinű Higgs bozont. Ekkor az S_z = ½ és S_z = -½ állapotok szuperpozíciós súlya megegyezik, és nulla lesz a részecske spinjének várható értéke, tömege viszont mégis lehet. Tehát a Higgs bozon olyan állapotot reprezentál, amelyben a spin két sodrásiránya „egybe van csomagolva” a szuperpozíciós elv révén.

Végkövetkeztetésként megállapíthatjuk, hogy a relativisztikus kovariancia elvből a részecskék három alapvető kettősségére következtethetünk: a spinre, a tömegre és a töltésre. Ez alapján is osztályozhatjuk a Standard Modell részecskevilágát. Az elektron típusú fermionok mindhárom alaptulajdonsággal rendelkeznek, a neutrínónak viszont csak spinje van.  A kvarkok is rendelkeznek spinnel, de mérésekkel detektálható töltésük és tömegük nincsen. A bozonok közül a fotonok csak spinnel rendelkeznek, a gyönge kölcsönhatás bozonjainak van spinje, tömege és lehet töltése is. A gluonoknak szintén van spinje, lehet töltésük is, de tömegükről nem beszélhetünk. Végül ott van a Higgs bozon, melynek csak tömege van, spinje nulla és várhatóan nulla a töltése is. A Higgs bozon tulajdonságainak ismerete jelenleg még nem tekinthető teljesnek.

 A blog további írásai elérhetők: "Paradigmaváltás a fizikában"

Ha színházba megyünk és a távolról nem látjuk jól a színészek arcvonásait, segíthetünk ezen egy látcsővel, amelyen közelebb látszik a színpad, jobban láthatjuk az arcokon az érzelmek tükröződését. Ha egy tiszta éjszakán az égboltra tekintünk, és jobban akarjuk látni a csillagokat, szintén a távcső segít, felnagyítva és jobban láthatóvá téve a különböző égi objektumokat. Kicsit bonyolultabb, de hasonló dolog történik, ha felülünk egy űrhajóba, amely a fénysebesség közelébe repít minket. A kabinban semmi szokatlant nem tapasztalunk, amikor nagy sebességgel egyenletesen haladunk, nem lesz semmi sem kisebb, vagy nagyobb, a kabin tárgyai akkorák maradnak, mint induláskor, de mégis ha kinézünk az ablakon a csillagvilág képe egészen más lesz, mintha csak távcsőbe néznénk. Pillantsunk előre és azt látjuk, hogy az előttünk lévő csillagok sokkal közelebb kerülnek hozzánk, de nézzünk hátrafelé is, bár távolodunk, mégis az égi objektumok közelebb látszanak, mint indulásunk előtt. Ugyanakkor jelentősen különbözik ez a látvány a szokásostól, mert megváltoztatja a színeket, előttünk minden kékebbnek, mögöttünk minden vörösebbnek látszik. Továbbá, ha mellettünk robog egy másik űrhajó a miénkkel azonos sebességgel, annak nagyságában, távolságában és színében nem veszünk észre semmi változást, oldalirányban az űrhajó sebessége nem változtatja meg a látható világot. Van azonban egy még szokatlanabb dolog, egy olyan változás, amit az űrhajóban észre sem veszünk: lelassul óránk sebessége. De nem csak óránk fog ritkábban tiktakolni, életritmusunk is lelassul, így nem is gondolunk rá, hogy lassabban telik az idő. Csak abból derül ki az idő lassulása, hogy saját naptárunk szerint hamarabb érjük el célba vett csillagot, mint amire akár a fénysebesség is képes lenne. Viszont amikor a lassuló óra méri az időt, és hozzá hasonlítjuk az űrhajóból látható rövidebb távolságot, a fénysebesség értéke nem különbözik attól, amit a Földön is meghatározhatunk. Tehát a távolság rövidül, az idő lassabban telik, de a fénysebesség mégis állandó marad. Van még egy további észrevehetetlen változás is: ahogyan csökken a hosszúság, úgy növekszik meg a tömeg, de ezt se érzékeljük, mert a mérés alapjául szolgáló tömegegység is ugyanúgy nagyobb lesz.  Persze ezek a szokatlan jelenségek a Földtől való távolodás nagy sebességénél lesznek jelentősek. Alapul véve a fény 300 000 km/s sebességét, ha űrhajónk ennek 99,5 százalékával távolodik, azaz másodpercenként 298 500 kilométert tesz meg, akkor már 10-szeres a változások mértéke a relativitáselmélet Lorentz-kontrakciós szabálya szerint, amit a γ paraméter fejez ki:

A müonok meghosszabbodott élete

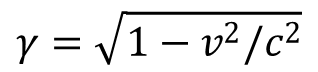
 Arra nincs igazán esély, hogy ekkora sebességre felgyorsítsuk űrhajónkat a hatalmas energiaigény miatt, de megvalósul a felső sztratoszférából érkező müonok esetén, melyeket a kozmikus sugárzás nagy energiájú protonjai hoznak létre, amikor ütköznek nagy magasságban a levegő molekuláival. A müonok példája azért érdekes, mert életük rövidre szabott, amikor a földi laboratóriumban képződnek élettartamuk (felezési idejük) 2,2 μs. Ez azt jelenti, hogy ennyi idő alatt számuk már felére csökken, és ez a feleződés exponenciálisan folytatódik. Ezek a részecskék 15 km magasságban jönnek létre, ahonnan még a fénynek is 50 μs időre van szüksége, hogy a Föld felszínére jusson. Azt várnánk tehát, hogy a földi laboratóriumokban alig figyelhetnénk meg müonokat. Összevetve azonban a sztratoszférában képződő müonok számát a felszínen megfigyelt mennyiséggel, a mérések azt mutatják, hogy a száguldó müonok élettartama tízszer hosszabb lett. Ezt persze mi mondjuk saját koordináta rendszerükben, a müonok viszont úgy „érzik”, hogy továbbra is 2,2 μs alatt feleződnek, csakhogy nekik 1,5 km volt a megtett útjuk a Lorentz-kontrakció miatt, és ehhez elég volt számukra 5 μs idő.

Az ikerparadoxon

Kétféle rendszerben gondolkozhatunk, a sajátunkban itt a földön állva, de gondolkozhatunk a müon száguldó rendszerében is. Mind a kettő ekvivalens inerciarendszer a relativitáselmélet szerint, érvényesül benne a fénysebesség állandósági szabálya, és ehhez kapcsolódóan azonos marad benne minden fizikai törvény. Mégis zavarba jövünk, amikor az ikerparadoxonról beszélünk. Az ikerparadoxon akkor lép fel, ha összekötjük az inerciarendszereket. Az ikrek egyike itt marad a Földön, a másik űrutazásban vesz részt. Az egyszerűség kedvéért ne foglalkozzunk avval a szakasszal, amíg felgyorsul az űrhajó, és nézzük csak azt, amikor az űrhajó már nagy sebességgel egyenletesen halad, azaz jogosan beszélünk inerciarendszerről. Ezt az indokolja, hogy az elvégzett kísérletek szerint nem számít a müon élettartama szempontjából, hogy mekkora volt a gyorsulás, amikor laboratóriumokban gyorsították fel a müonokat. Célszerű egyébként az űrhajó gyorsulását a földi 1 g = 9,83 m/s² értékűnek venni, mert ekkor az űrhajósokra a földi gravitációnak megfelelő erő fog nehezedni a hosszú út során. Kisebb gyorsulás persze hosszabb idő alatt fogja felgyorsítani az űrhajót, ami hozzájárul az ikrek korának eltéréséhez is, de most koncentráljunk arra a szakaszra, amikor már kikapcsoltuk a sugárhajtást, és az űrhajó sebessége nem változik. Ha innen számolva az űrhajó egy 10 fényévnyi körutat az 5 fényév távolságban lévő csillagig γ= 10 Lorentz-faktornak megfelelő sebességgel tesz meg, akkor ez számára csak 1 évet vesz igénybe. A földi ikerhez képest így az űrutas 9 évet nyert, ami már érzékelhető korkülönbség az ikrek között.

 Miért beszélünk paradoxonról? Ezt a két inerciarendszer ekvivalencia szabálya okozza! Az otthon maradó iker szemszögéből nézve, a hozzá képest nagy sebességgel (azaz nagy γ értékkel) halad, így hazatérve fiatalabb lesz nála. De hogy néz ki a helyzet az utazó iker rendszeréből nézve? Ő is a saját rendszeréhez hasonlítja az ikertestvér sebességét, hiszen a relativitás elve miatt nincs abszolút sebesség, csak az számít, hogy mekkora a különbség a két inerciarendszer sebessége között. Ez a sebesség ugyan fordított irányú, azaz negatív, de mivel a sebesség előjele közömbös a γ Lorentz-kontrakció számításánál, így az űrutas azt gondolhatná, hogy a földön maradó ikertestvér órája lassul le tízedére, tehát a találkozáskor a másik lesz fiatalabb. Az ellentmondás a két gondolkozás között nyilvánvaló!

Van-e abszolút referencia rendszer?

Kinek van igaza, melyik állandó sebességű inerciarendszer alapján kell számolni? Talán mégis lenne egy abszolút vonatkoztatási rendszer, ami alapul szolgálhat az űrhajó sebessége szempontjából?

Ha elfogadjuk a Lorentz-szabály érvényességét, csak arra gondolhatunk, hogy a két inerciarendszer mégsem ekvivalens: a számítás csak az egyik inerciarendszerben ad helyes eredményt.  De milyen alapon választjuk ki a helyes rendszert? A szokásos magyarázat a gyorsulásra hivatkozik, mondván az utazó iker gyorsult és lassult, míg a másik helyben maradt, és az aszimmetrikus előélet okozza a különbséget. Ezt magyarázza hosszasan a wikipedia angol nyelvű cikke is, ahol olyan számításokat végeznek el, amiben csak a gyorsulásról és lassulásról esik szó, és nem tárgyalják az állandó sebességű szakaszt. De ha a gyorsulás-lassulás a lényeg, akkor miért jön létre korkülönbség az egyenletes sebességű szakaszban is, mégpedig arányosan avval, hogy milyen hosszú ideig volt a két rendszer sebessége különböző? A müonnal elvégzett laboratóriumi kísérletek, ahol óriási gyorsulást alkalmaztak, szintén arra mutat, hogy nem számít a tényleges gyorsulás nagysága.

Az impulzusmegmaradás kulcsszerepe

 A helyes választ segít megtalálni az impulzusmegmaradás törvénye, ami egyúttal kapcsolódik a minimális mozgási energia megtalálásához is. Az űrhajó indulása előtt a földi rendszer része volt, és jelöljük a Föld és az űrhajó tömegét „M” és „m” betűkkel. A kilövés után megadhatjuk az űrhajó „v” sebességét a Földhöz képest, vagy fordítva, a Föld „V” sebessége „-v” lesz, ha az űrhajó sebességét vesszük nullának.  A józanész az előbbit tartja helyesnek, és igaza van, ha a nagyságrendet tekintjük alapnak, hiszen az űrhajó tömege elhanyagolható a Földhöz képest. Ha nagyon precízek vagyunk, persze bevezethetjük a súlyponti rendszert. Ebben az impulzus összege nulla lesz, vagyis m·v =  ̶M·V. Ha nem a súlyponti rendszert veszem alapul megszegem az impulzusmegmaradási törvényt, ezért a törvény megtartása már kijelöli a helyes vonatkoztatási rendszert, amelyik persze gyakorlatilag egyezik a Földével.  A reális sebesség az energia abszolút nagyságának kiszámítása miatt fontos. A kinetikus energia a sebesség négyzetével arányos, emiatt bár a Föld és az űrhajó impulzusa egyenlő a kilövés után, a Föld mozgási energiája elhanyagolható az űrhajóhoz képest. A Földhöz viszonyított rendszer kitüntetett szerepe megmarad akkor is, ha rakétákkal, vagy sugárhajtó művel tovább gyorsítjuk az űrhajót. Nagy sebességeknél már a relativitáselmélet kovariancia elve szerint kell számolni az energiát, amely figyelembe veszi az m₀ nyugalmi tömeghez tartozó E₀ = m₀c² energiát is. A kovariancia törvény szerint:

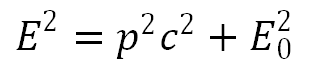
Itt p = m·v az impulzus. Figyelembe véve a tömeg-energia ekvivalencia törvényt, amely szerint E = mc², azt kapjuk, hogy a mozgás által megnövelt energia arányát a nyugalmi energiához képest, szintén a Lorentz-faktor adja meg:

E = E₀/γ

Az energia és idő kapcsolata

Az energiának kulcsszerepe van az óra lassulásának számításában. Planck felismerése szerint a fotonok energiája a frekvenciával arányos, ami úgy is megfogalmazható, hogy az energia a hullám T periódus idejével fordítottan arányos:

E = h·f = h/T

A kvantummechanika felismerése, hogy valamennyi részecske rendelkezik hullámtermészettel, amiért az E·T = h szabály érvényes a mikrovilág valamennyi objektumára és az ezekből felépülő makro objektumokra is. Legyen szó akár a parányi müonról, vagy az űrhajóról, az objektum „v” sebessége határozza meg a periódus idő növekedését a Lorentz-faktoron keresztül:

T = γT₀

Ez az óra lassulásának törvénye, amit szokás az idő dilatációjának is nevezni. A törvényből az is következik, hogy a fény sebessége az űrhajó rendszerében is ugyanakkora, hiszen a fény által megtett út is ebben az arányban csökken. A Lorentz-faktorban a sebesség nagysága attól függ, hogy melyik inerciarendszer a viszonyítás alapja. Ha minden inerciarendszer ekvivalens, akkor az idő dilatációja csak látszólagos jelenség, ez csak akkor válik valóságossá, ha van valamilyen fizikai ok, ami megkülönbözteti a referencia rendszert az összes többitől. Ilyen fizikai ok, ha a vizsgált fizikai objektum egy nagyobb rendszer része volt, és az onnan való kilépés energia befektetéssel jár együtt. Ekkor az elkülönített rendszer szempontjából az induló rendszer tömeg középpontja már kitüntetett szerepet játszik, és ehhez viszonyítva az idő dilatáció látszólagossága már mérhető fizikai mennyiséggé válik.

Idő dilatáció gravitációs mezőben

Az idő dilatáció másik formája, amikor az óra lelassul gravitációs erőmezőben, ennek szabályát az általános relativitáselmélet alapján adja meg a szakmai irodalom. Ha azonban eltekintünk az extrém erős gravitációs mezőtől, hasonló eredményre juthatunk Newton gravitációs törvényből is. Fogadjuk el azt az alapelvet, hogy

 bármilyen energianövelő folyamat idő dilatációt okoz, amelynek mértékét a nyugalmi energiához viszonyított teljes energia határozza meg a γ = E₀/E összefüggés szerint.

Evvel kiterjesztjük a Lorentz-faktor fogalmát más jelenségekre is, amely nem kötődik ahhoz, hogy milyen tagok járulnak hozzá az energiához, így ez vonatkozik a potenciális energiára is. Ennek egyik formája a gravitációs energia V = GMm/R. Vonzó erő esetén a potenciális energia negatív, taszítás esetén pozitív, ami a gyorsulás iránya szempontjából fontos, de nem befolyásolja, hogy mekkora a sebesség négyzetének, azaz a kinetikus energiának változása. Emiatt a gravitáció energia megnöveli az E₀ nyugalmi energiát az effektív Lorentz-faktor számításánál:

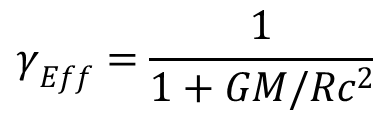
A formulában szerepel az általános gravitációs állandó G = 6,673·10^-11 m³/kg·s²,  a Föld tömege M = 5,9722·10²⁴ kg, valamint a sugara R = 6371 km.

A Hafele-Keating kísérlet

1971-ben egy fizikus és egy csillagász, mégpedig Joseph C. Hafele és Richard Keating, gondoltak egy nagyot, és atomórákkal zsebükben útra keltek, hogy ellenőrizzék a speciális és általános relativitáselméletet az idő dilatáció kimutatásával. Először kelet felé, majd nyugat felé repülték körbe a Földet, majd a körút végén összehasonlították az utazó órákat az otthon letétbe helyezett masinákkal. Az összehasonlítás eredménye az lett, hogy kelet felé haladva az óra 59 ns késést, nyugat felé 273 ns sietést szedett össze.

Végezzünk becslést, hogy lássuk a nagyságrendeket! Ehhez alapul lehet venni, hogy a gépek átlagban 1000 km/óra sebességgel repültek és az átlagos magasság 10 km volt. Ez azt jelenti, hogy a földön hagyott óra R értéke a Föld középpontjától számítva 6371 km, amely megnőtt 6381 kilométerre a repülés során. Ekkor az utazó és a földön maradt órák γ_Eff faktorainak különbsége 1,089·10^-12. Ha Washington magasságában körbe utazzuk a Földet, akkor 33 000 kilométert kell megtenni, ami 1000 km/óra sebesség esetén 33 nettó óra alatt tehető meg. Természetesen az utazási idő és távolság hosszabb a menetrend szerinti légi járatokon, mert azok pályája nem pontosan követi a kelet-nyugati irányt. Vizsgáljuk meg a két kísérletező által megadott adatokat! Az általános relativitáselmélet alapján kiszámították, hogy kelet felé utazás során 144 ns, nyugat felé 179 ns sietés lenne várható, a különbség főleg az utazás eltérő idejéből származik. Felhasználva a γ_Eff dilatációs faktorok előbb megadott különbségét, egyezést kapunk Hafele-Keating számításával, ha a kísérletezők effektív utazási ideje 36,7, illetve 45,7 óra volt. Az így becsült utazási idők reális hossza arra utal, hogy a Newton formulára alapozott effektív Lorentz-faktor akkora értéket ad az idő dilatációra, mint az általános relativitáselmélet.  

Az idő dilatáció másik összetevőjét a repülőgépek sebességéből kell kiszámítani. Itt az alapkérdés, hogy mihez kell viszonyítani a repülő sebességét, a Földhöz, a Naphoz, esetleg az egész Tejúthoz, netán valamilyen éterhez?

Amikor a szokásos módon beszélünk a repülők sebességéről, azt a Földhöz viszonyítjuk. Ha ez alapján számítjuk ki a Lorentz-faktort, nem tudjuk megmagyarázni, hogy miért siet az atomóra, ha nyugat felé haladunk, és miért késik kelet felé. Tehát a Föld forgását is számításba kell venni! De ha már a Föld forgási iránya szóba jön, válaszolni kell a kérdésre, hogy a Föld mihez képest forog? A kopernikuszi válasz után nem lehet kétséges, hogy nem a Nap kering a Föld körül, hanem a Föld forog saját tengelye körül. A Nap-Föld rendszer teljes mozgási energiájának számításánál reális értéket akkor kapunk, ha a Naphoz viszonyítjuk a sebességeket az égitest óriási tömege miatt. Persze a pontos számítás a súlyponti rendszerből végezhető el, de nem követünk el nagy hibát, ha maradunk a Naphoz kötött koordinátáknál. A repülő nem szakad ki a Föld vonzáskörzetéből, hanem együtt halad vele, ezért a Nap forgása és égi útja a Tejútban nem játszik szerepet. Más lenne a helyzet egy olyan kísérletben, ahol már Nap körüli pályákat hasonlítanánk össze, ahol a Nap tengelyforgási irányával egyező és az avval ellentétes pályán mozgó órák idő dilatációját vetnénk össze.  Ekkor már nem kerülhetnénk meg a kérdést, hogy mihez képest forog a Nap, és valamilyen galaktikához kötött inerciarendszerben kapnánk a helyes eredményt.

 De maradjunk itt a földön! A Föld körberepülése nagyjából a 38 szélességi fok körül történt a 33 000 km hosszú délkörön, ahol a földforgás kerületi sebessége 1380 km/óra, ehhez kell a repülő Naphoz képesti sebességét viszonyítani, ami 380 km/óra nyugat felé és 2380 km/óra kelet felé. Hasonlítsuk össze a Lorentz-faktorokat, amikor kelet, illetve nyugat felé halad a gép levonva ebből a Föld felszínén tartott órára vonatkozó értéket. A különbség nyugat felé 0,7545·10^-12 (az óra siet), kelet felé  ̶1,612·10^-12 (az óra késik) lesz. Szorozzuk meg ezeket a különbségeket a 33 órás névleges idővel, ekkor kelet felé 90 ns sietést, kelet felé -192 ns késést kapunk. Az így becsült értékek közel vannak a Hafele és Keating részletes számításának eredményével, amely 96 ns és -184 ns volt. Úgyszintén a gravitációs és kinematikai járulékok összege jól reprodukálja az atomórák által szolgáltatott adatokat. Megállapíthatjuk, hogy az a referencia rendszer, amelyet a Naphoz kötünk, jól magyarázza a mért idő dilatációt. Másképp fogalmazva, az idő dilatációjának mérésével megtalálhatjuk a súlyponti rendszert, amelyben a mozgási energia összege minimális.

A gyorsulás és gravitáció ekvivalenciája

Az általános relativitáselmélet kiindulópontja, hogy a gyorsuló rendszerben fellépő tehetetlenségi erő nem különböztethető meg a gravitációtól, ez az Einstein által megfogalmazott ekvivalencia tétel. Ha ez így van, akkor ebből az következik, hogy a gyorsulás együtt jár az idő dilatációjával. Nézzük meg ennek mértékét a fénysebességtől távoli tartományban! A Newton egyenlet szerint az erő a tömeg és a gyorsulás szorzata: F = m·a. Az erővel szemben végzett munkavégzés hozza létre az energianövekedést:  ΔE = F·s, ahol az adott közelítésben s = ½a·t², ha álló helyzetből indulunk. Az így számítható energia a mozgási energiának felel meg: ΔE = ½m·a²t² = ½m·v². Ezt a növekményt figyelembe véve az effektív Lorentz-faktor:

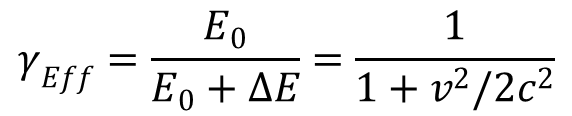
Kis sebességeknél ez pontosan megfelel a szokásos Lorentz-faktornak. Ez azt mutatja, hogy az idő dilatáció kizárólag az elért sebességtől függ bármekkora is legyen a gyorsulás. A gyorsulásnak csak abban van szerepe, hogy mennyi idő alatt érünk el valamekkora sebességet. Más szóval a gravitációval ekvivalens gyorsulás nem hoz létre többleteffektust, ahhoz képest, amit a speciális relativitáselmélet már megadott. Ha azonban összehasonlítjuk az idő dilatációját eltérő nagyságú gravitációs mezőben (például az egyik óra legyen geostacionárius pályán, a másik pedig a földön), akkor az órák sebessége eltérő lesz. A Föld körül keringő műholdak esetén a centrifugális erő kiegyenlítő hatása hozza létre a súlytalanságot, a földön állva egy felfelé ható kényszererő akadályozza meg a szabadesést. Sem a centrifugális erő, sem a kényszererő nem játszik szerepet az objektum energiájában, mert nem hoznak létre elmozdulást a külső erő irányában, azt csak kiegyenlítik. Energianövelő hatás nélkül pedig nem járulnak hozzá az idő dilatációjához sem.

Az energiamérleg szerepe

 A Hafele-Keating kísérletből nyert tapasztalatok alapján könnyebben megérthetjük az ikerparadoxont is. Az alap a szétválasztás, amikor az egységes rendszer egy része külön válik elrugaszkodva onnan. Ez történik a müon útra indulásakor is, mert a földi rendszerhez tartozó levegőmolekula kap egy nagy lökést a kozmikus sugárzás protonjaitól, amely energiája révén kiemeli ezt a részecskét a Földhöz kötött inerciarendszerből. Ez a mozgási energia nyereség lesz a forrása a meghosszabbodott felezési időnek.  Az űrhajó is leválik a földi rendszerről, amikor óriási energia befektetés árán útnak indul és gyorsítja sebességét. Mindkét esetben a nagyrendszer tényleges (nem csak elképzelt!) energiát ad át a részrendszernek, amelynek ezáltal sokszorosan megnő az energiája az eredeti m₀c² nyugalmi energiához képest.  A lényeg tehát az energiamérleg! Ez dönti el, vajon a müon, illetve a száguldó űrhajó rendszerét kell-e alapul venni a számításokban, vagy a földi rendszert. Ha az űrhajó rendszeréhez viszonyítjuk saját sebességünket, azt nullának vesszük, amihez nem tartozik kinetikus energia. Viszont ebben a rendszerben a Föld fog közel fénysebességgel mozogni, melynek kiszámítva kinetikus energiáját óriási értéket kapunk. De ez csak számítás, csak fikció, hiszen mitől nőtt volna meg a Föld mozgási energiája?  Az energiacsere iránya nem válaszható meg önkényesen, nagyon is valóságosan kell befektetnünk rengeteg energiát a gyorsításhoz. Szintén valóságos folyamat, ahogy a kozmikus sugárzás protonja átalakítja a levegőmolekulát, és nagy sebességet ad a kirepülő müonnak. Az inerciarendszereket az energiaátadás iránya különböztet meg. Az ekvivalencia csak egy matematikai, transzformációs szabály, amely kimondja, hogy a leírás szempontjából nincs különbség a két inerciarendszer között, mindkettőben azonosak fizikai törvényeink, de ez csak addig igaz, amíg nem teremtünk valóságos kapcsolatot a két különböző sebességű rendszer között, amíg nem gondolunk arra, hogy honnan is származik a mozgó rendszer energiája. Általánosságban ugyan nem létezik kitüntetett referencia rendszer, de ha energia befektetéssel létrehozunk egy új rendszert, annak számára az induló rendszer kitüntetett lesz.

 Amikor az ikertestvér visszatér a hosszú útról, elveszíti a korábban felvett mozgási energiát, hiszen a Földhöz képest ekkor már nem mozog. Az ikrek közötti korkülönbség fejezi ki a rendszer „emlékezetét” arra a körülményre, hogy a felgyorsított rendszer milyen hosszú ideig volt energiával feltöltött állapotban az induló rendszerhez viszonyítva.

Visszatérés a múltba

A legfontosabb megállapítás, hogy a matematikai ekvivalencia nem jelent egyúttal fizikai egyenértékűséget is, ennek hiánya viszont csak tényleges összehasonlításkor derül ki. A dilemma oka, hogy a Lorentz-kontrakció a sebesség négyzetével arányos. Ehhez kapcsolódik az idő irányának megfordítása is. Ha visszamennénk a múltba, a sebesség előjele megfordulna, de a négyzete azonos marad. Emiatt ugyan az időben előre, vagy visszafelé haladás matematikailag ekvivalens művelet, az idő iránya mégsem fordítható meg, amit a fizika a termodinamikai entrópia törvényével magyaráz. Az idő megfordíthatatlansága tükröződik az ikerparadoxonban is: fiatalabbak nem lehetünk, csak kevésbé idősek. Nem irigyelhetjük az űrutast azért sem, mert bár naptári években számolva tovább élhet, de a hosszú út alatt megtakarított idő egyúttal kevesebb élményt is jelent.

Összefoglalás

Az inerciarendszerek ekvivalenciája a relativitáselméletben azokra a megfigyelésekre korlátozódik, amelyekben a fotonok frekvenciája az alap. A frekvenciát két állapot energiakülönbsége szabja meg, amit nem befolyásol az energia nullapontjának megválasztása. Az idő dilatáció mérése viszont új lehetőséget nyit meg, mert ez már az energiaarányokról nyújt felvilágosítást. Az arány alapja az m₀c² nyugalmi energiához való viszonyítás. Ekkor az energia nullapontja nem választható meg önkényesen, mert evvel felborítanánk az arányokat. Eltérő sebességű rendszerekben az idő dilatáció, a tér kontrakció, vagy a tömegnövekedés csak látszólagos jelenségek, mindaddig, amíg nem teremtünk valódi fizikai kapcsolatot két inerciarendszer között. Ha viszont energia befektetés árán szétválasztjuk, majd összekötjük az inerciarendszereket, már átformálódik a látszatok relativisztikus világa, a látszatból valóság lesz!

Az idő dilatáció jelensége az energiához kapcsolódik, és nem korlátozódik a mozgási és gravitációs energiára, nem indokolja ezért semmi sem, hogy ne lépne fel más erőmezőben is. Megérné ennek kísérletileg utánanézni, elektromágneses mezőben megfigyelve rövid élettartamú részecskék, vagy radioaktív izotópok felezési idejét. Ilyen lehetne a szén C-11-es izotópja, amelynek felezési ideje 20 perc és ennek értéke egy ezrelék pontossággal ismert. Ez a határ már elérhető, ha a C-11 atommagokat 2 millió voltos elektromos térbe helyezzük el.   

A blog további írásai: Paradigmaváltás a fizikában

3. 3. Látogatás a részecskék szerelőműhelyében: a gyenge kölcsönhatás

Az előző két részben (első, második) azt kerestük, hogyan találjuk meg a kapcsolatot a gravitáció, az elektromágnesség és az erős kölcsönhatás között a fénysebességű forgások koncepciója alapján. Ez a közös alap nem a mezőelméletek alapelve, a kvantum volt, hanem a tér forgásai. Amíg ez a forgás fénysebességgel megy végbe az elektromágnesességet közvetítő fotonok és az erős kölcsönhatás gluonjai esetén, a gravitáció kettős forgásai lassulnak a távolsággal a Kepler szabály szerint, és messze elmaradnak a fénysebesség mögött. A közvetítő eszköz tehát nem a szokásos bozon a gravitációnál, amihez S = 1 spint rendelhetünk, hanem egy láthatatlan – ha úgy tetszik virtuális – forgás, amit formálisan S = 0 spinnel jelölhetünk. A részecskét alkotó fénysebességű kettős forgások bocsátják ki ezeket a lassú gömbhullámokban terjedő forgásokat, melyek emissziós és abszorpciós egyensúlya alakítja ki a gravitációs potenciált a térben okozott görbületek révén.

Ebben a záró részben tesszük meg a következő lépést, amelyben megvizsgáljuk, hogyan alakulnak át egymásba az elemi részecskék a gyenge kölcsönhatás által, és milyen szemléletes képet tud adni erről a fénysebességű forgások koncepciója. Ez a rész jelentős mértékben „A rejtélyes gyenge kölcsönhatás” című korábbi íráson alapul.

3. 1. Két kölcsönhatás eltérő világa

Aligha lehetne két jobban eltérő kölcsönhatást találni, mint az elektromágneses és a gyenge kölcsönhatás. Az elektromágnesesség közvetítője a foton akár milliárd fényév távolságból is megérkezhet hozzánk egy távoli galaxisból, szemben a gyenge kölcsönhatást közvetítő W és Z bozonokkal, melyek hatótávolsága az atommagnál is kisebb, úgy 10^–16 m nagyságába esik. Elmondható ez az élettartalmukról is, a távoli galaxisokból érkező foton milliárd éves utazás után is megfigyelhető, míg a W bozon élettartama nem hosszabb 10^–24 másodpercnél. Szintén nagyon eltérnek tömegükben és töltésükben is, a fotonnak nincs is nyugalmi tömege, míg a két gyenge kölcsönhatási bozon a részecskevilág nehézsúlyú bajnoka, ha eltekintünk a Higgs bozonnak tulajdonított részecske tömegétől, akkor valamennyi megfigyelhető részecske tömegét meghaladja a W és Z bozoné. Ami pedig a töltésüket illeti, a fotonnak nincs töltése, viszont a W bozonnak van, mégpedig a +e illetve –e elemi töltés, hasonlóan az elektronhoz és a pozitronhoz. A W⁺ és W^– egymás részecske-antirészecske párja, míg a fotonok világa nem ismeri ezt a kettősséget. Abban is nagy a különbség, hogy amíg az elektromágneses erőhatás vonzás, vagy taszítás  két objektum között, addig a gyenge-kölcsönhatás szerepe, hogy átalakítsa a részecskéket egymásba.  Abban is különböznek, hogy az elektromágneses kölcsönhatás csak töltött objektumokra hat, viszont a gyenge kölcsönhatásban minden részecske részesül. Csupán egy dologban egyeznek: spinjük egyaránt S = 1, azaz bozonokról van szó. Másrészt viszont sokkal nagyobb a hasonlóság az elektromágnesesség és a gravitáció között, nézzük akár az időtávot, vagy a kölcsönhatások távolságfüggését. Ezért hatott a fizikus társadalomban meglepetés erejével, hogy a gyönge és elektromágneses kölcsönhatás közös elméleti alapra helyezhető (elektrogyenge kölcsönhatás), míg a gravitáció nem volt bevonható az egyesített mezőelméletbe (Sheldon Glashow. Steven Weinberg, Abdus Salam, Nobel díj: 1979).    

3. 2. Az átalakulások megmaradási elvei

A gyenge és elektromágneses kölcsönhatás eltérésének és ugyanakkor mélyen fekvő hasonlóságának megértéséhez szemléletes kulcsot ad a részecskék fénysebességű forgásmodellje. Először azt kell megértenünk, hogy milyen állapotváltozást hoz létre a két kölcsönhatás. Az elektromágnesesség hatását legkönnyebb az elektron példájával szemléltetni. Az atomban, vagy molekulában kötött elektron pályáját az impulzusnyomatékkal jellemezhetjük, melynek értéke a redukált Planck-állandóval fejezhető ki: Lℏ, ahol az L egész szám a pályamozgás kvantuma.  Az elektron állapotváltozása során az L kvantumszám eggyel változik, legyen szó foton elnyelésről (abszorpció), vagy kibocsátásról (emisszió). Ilyenkor az elektron pályaugrása hozza létre, vagy tünteti el a foton S = 1 spinjét, azaz annak ℏ nagyságú impulzusnyomatékát.  Szemléletesen úgy mondhatjuk, hogy az elektron „keringő” mozgása konvertálódik a foton saját forgásává. Hasonló magyarázat adható, amikor értelmezzük mágneses mezőben Larmor-precessziót végző S = ½ spinű elektronok rezonancia átmeneteit, ekkor a foton abszorpciója, vagy emissziója során a spin mágneses mező irányú komponense egységnyit változik (szokásos jelölésben S_z értéke +½ és  ̶½ között ugrik). Ebben az esetben a mágneses mezőben polarizált elektronspin megváltozása biztosít forrást a foton impulzusnyomatékához. Mindkét esetben az energiamegmaradás mellett az impulzusnyomaték megmaradása vezet a kvantumátmenetek kiválasztási szabályához. Ehhez még hozzá kell tenni, hogy az átmenetek során az elektronok nyugalmi tömege ugyanannyi marad.

3. 3. Annihiláció és párképződés

Létezik egy másik kapcsolat is a fotonok és a részecskék között, az annihiláció és a párképződés. Az előbbi esetben egy azonos tömegű részecske és antirészecske eltűnik gamma-sugárzás létrejöttével, a másik folyamat ennek fordítottja, amikor létrehoz a foton egy részecske-antirészecske párt, például egy elektront és egy pozitront. Az utóbbi folyamathoz szükséges egy „ütköző” atom is az impulzusmegmaradás miatt. Ezek a folyamatok mutatják, hogy a nyugalmi tömeg képződhet is, meg el is tűnhet, vagyis a nyugalmi tömeg a mikro folyamatokban nem megmaradó mennyiség.  Az átalakulások kiválasztási szabálya viszont, hogy az energia, a töltés és a spin (impulzusnyomaték) megmaradjon.  Mivel a fotonnak nincs töltése, ez a szabály azt jelenti, hogy a képződő két részecske ellentétes előjelű töltéssel rendelkezik, másrészt a foton S = 1 spinje megköveteli, hogy a két új részecske egyaránt ½ spinnel rendelkezzen. A fénysebességű forgásmodellben a feltétel azáltal teljesül, hogy az elektron és pozitron kettős forgásának ellentétes a kiralitása, és így az annihiláció során kioltódik az egyik forgás az ellentétes sodrásirány miatt, miközben a másik forgás mindkét részecskénél megmarad, ez a megmaradó forgás pedig nem más, mint két gamma foton. A kettős forgás egyik komponensének megszűnéséhez az is kell, hogy a frekvenciák megegyezzenek, azaz csak két azonos nyugalmi tömegű részecske és antirészecske semmisítheti meg egymást. Párképződéskor viszont megfordul a helyzet, ekkor a fénysebességű haladó mozgás két ellentétes perdületű forgásra hasad fel, amiért a képződő kettős forgások kiralitása, azaz töltése ellenkező előjelű lesz, a foton ℏ impulzusnyomatéka pedig két egyenlő részre válik szét.

3. 4. Leptonok

3.4.1. Az elektroncsalád tagjai

Térjünk át a részecskeátalakulások megmaradási szabályaira! Nézzük meg ehhez az elektron (e) és „nagy testvérei” a müon (μ) és a tau részecske (τ) esetét! Ezek a töltött leptonok, amit „anyagnak” nevezünk, ha a töltés negatív, és „antianyagnak”, ha pozitív. Szintén a leptonok közé tartoznak a töltéssel nem rendelkező neutrínók (ν). Ebben a „családban” a töltés és a spin azonos, viszont a nyugalmi tömeg erősen különbözik, a müon tömege 207-szer, a tau részecskéké 3477-szer nagyobb az elektronhoz képest. (A három részecske energiája: 0,511 illetve 105,66 és 1776,8 MeV.) Honnan származnak ezek az arányok? Erre a részecskék tulajdonságait összegző Standard Modell sem adja meg a választ, ezért ezeket az értékeket fogadjuk el, mint kísérleti tapasztalatot. A két nehezebb részecske viszonylag rövid életű szemben a stabilis elektronnal: müon: 2,2x10^–6 s, tau: 2,9x10^–13 s, és bomlásuk egyik végterméke az elektron. A részecskevilágban ez az élettartam nem számít rövidnek, mert amikor gamma-sugárzás jön létre más részecskék bomlásakor, a tipikus felezési idő 10^̶–20 s. A viszonylag lassú bomlás oka, hogy leptonoknál egyedül a gyenge kölcsönhatás játszik szerepet, mert itt az elektromágneses átmenet tiltott.

3.4.2. Neutrínók a konzekvens kvantummechanika tükrében

Hogyan lehet a másik leptont, a neutrínót is leírni fénysebességű forgásokkal?  Ehhez kölcsön kell venni a kvantummechanikából a szuperpozíció elvét. Ez kimondja, ha valamilyen mikro objektum mozgását két független szimmetrikus pálya – azaz állapotfüggvény – jellemzi, akkor ezek szuperpozíciója is az energiaoperátor sajátfüggvénye lesz. Ha nincs jelen külső elektromos mező, akkor az elektron és pozitron energiája is azonos, mert csupán a királis szimmetriában térnek el. A fénysebességű forgás koncepciója a tér lokális kettős forgásaival azonosítja a fermionokat, ezért az elektron és pozitron kettős forgásaiból kialakulnak különböző lineáris kombinációk. Ha a két királis forgás részaránya egyenlő, akkor az ellentétesen oszcilláló Coriolis erők semlegesítik egymást, és így a mozgási állapotnak nulla lesz a töltése, vagyis nem hat rá az elektromágneses kölcsönhatás. Ez a mozgásforma a neutrínó, amit rendkívül nehéz megfigyelni, mert csupán a gyenge kölcsönhatás révén ad hírt magáról. De ugyanígy a müon és antimüon, illetve a tau és antitau részecskék is alkothatnak semleges töltésű szuperpozíciót, ezért három különböző neutrínóról beszélhetünk.

A neutrínók elmélete több nyitott kérdést vet fel. Az egyik ilyen, hogy létezik-e antineutrínó, vagy pedig a neutrínó önmagának az antirészecskéje. A másik, hogy a kísérletek tanúsága szerint a neutrínó sebessége egyezik a fénysebességgel a mérési pontosság határain belül, ugyanakkor a három neutrínó között oszcilláció lép fel a fluxus vizsgálatok szerint. Ugyanis a különböző égi objektumból érkező neutrínó fluxus kisebb, mint amit az elmélet megkíván, és ez magyarázható, ha oszcilláció jön létre a három típus között. A fénysebességű mozgás viszont csak nulla tömegű részecskék számára lehetséges, de akkor miben különbözik a neutrínó három típusa? Ezekre a kérdésekre keresi a választ a konzisztens kvantummechanika felvetése: (Antal Rockenbauer: „Consequent Quantum Mechanics by Applying 8-Dimensional Spinors in the Dirac Equation”, Physical Science International Journal, 2020, 24, 27-31). Az elképzelés abból indul ki, hogy amíg a szokásos kvantummechanika az energiához, impulzushoz és impulzusnyomatékhoz operátorokat rendel, addig a töltést és tömeget mint konstansokat kezeli. Kiindulva a relativitáselmélet kovariancia törvényéből, amely az energia négyzetét az impulzustag és a nyugalmi energia négyzeteként állítja elő, a publikáció bemutat egy olyan lehetőségét, amikor a Dirac által javasolt négydimenziós spinor felbontás helyett a négyzetgyökvonást nyolcdimenziós spinorokkal végezzük el, ahol már a töltést és a tömeget is a spinhez hasonló operátorok írják le. A módszer olyan általános fermion egyenletet eredményez, amelyben az elektront, az up és down kvarkokat, valamint a neutrínókat, egyaránt le lehet írni egy új kvantumszámmal, amely az elemi töltés háromszorosa. A neutrínók sajátsága ebben a leírásban, hogy jól definiált impulzussal rendelkeznek, viszont tömegük várhatóértéke nulla, akárcsak a fotonnak. Ez már lehetővé teszi, hogy a neutrínók a fotonhoz hasonlóan fénysebességgel haladjanak, miközben különböző impulzusuk miatt oszcillálhatnak is. Az alkalmazott formalizmus szerint nincs külön antineutrínó, azaz a neutrínó önmagának az antirészecskéje.

Kvarkok esetén a két királis állapot súlyaránya eltérő, amit az erős kölcsönhatás idéz elő. A kiralitás eltérő mértéke értelmezi a törtöltéseket, és magyarázza, hogy ilyen részecske szabadon nem figyelhető meg, mert képződésük alapfeltétele az erős kölcsönhatás, ami viszont szabad állapotban nincs jelen.

3. 5. A gyönge-kölcsönhatási bozon spirálmozgása

Az előző pontban említettük, hogy a müon és a tau részecske nem stabilis, és a bomlás során elektron jön létre neutrínók kíséretében. Az első kérdés, ami felmerül, hogy miért nem gamma-sugárzás kibocsátásával megy végbe az átalakulás, hiszen ekkor sem a spin megmaradás, sem a töltésmegmaradás szabálya nem sérülne (a töltés nem változik, a spin vetületi kvantumszám ugrását ½ és –½ között pedig kiegyenlíti a foton S = 1 spinje). Az ilyen átmenet tiltását a részecskék fénysebességű forgásmodelljével értelmezhetjük. A foton egytengelyű forgás, amely a fermion kéttengelyű forgása közül csak az egyiket tudja megváltoztatni. Ahhoz, hogy mindkét forgási frekvencia megváltozzon (a müon és tau csak a forgási frekvenciában tér el az elektrontól!), két lépésre van szükség. Első lépésben a gyenge kölcsönhatás a töltést és a tömeget az egytengelyű forgásnak adja át (W^- bozon, S = 1), de létrehoz egy töltés semleges és tömeggel nem rendelkező fermiont is (neutrínó, S = ½), amely a kettősforgás jelleget viszi tovább. Az impulzusnyomaték megmaradási törvényét, amit a spinek összegzési szabályai írnak le, úgy is felfoghatjuk mint a forgások számának megmaradási törvényét. A tau részecske bomláskor beszélünk tau neutrínóról, müon bomláskor müon neutrínóról, míg az elektron neutrínó az elektronok képződésében játszik szerepet.

 A bomláskor képződő W bozon tehát jelentősen különbözik a fotontól, hiszen átveszi a müon töltését és van jelentős tömege is, mégpedig jóval nagyobb a tömege, mint amekkorával a kibocsátó fermion rendelkezett. Ezt úgy foghatjuk fel, hogy rendkívül rövid időre – ez a már említett 10^-24 s – létrejön a térben egy akkora görbület, amelynek potenciális energiája ellentételezi a W bozon képződési energiáját. Mivel a W bozon egytengelyű forgás, csak úgy lehet töltése, ha a forgáshoz olyan haladó mozgás kapcsolódik, amely merőleges a forgási tengelyre, ez ugyanis a  Coriolis-erő fellépésének feltétele. Ez a másodlagos mozgás a forgási sugarat fénysebességgel növelni fogja, ami spirális kialakulásához vezet, ahol a sugárnövekedést az r = r₀ + ct összefüggés írja le. Itt r₀ = h/m₀c a W bozon Compton-sugara. Az ω körfrekvenciájú forgás kerületi sebessége c = ωr, ezért a sugárnövekedés a körfrekvencia csökkenésével jár az

egyenlet szerint, ahol az ω₀ frekvencia a W bozon m₀ tömegéből számolható a ℏω₀ = m₀c² ekvivalencia elv alapján. A frekvenciacsökkenés a tömeg, illetve a részecske energiájának csökkenését hozza magával. A W bozon kísérletileg meghatározott tömegét ezért lokális képződési tömegnek kell tekinteni és nem nyugalmi tömegnek, hiszen a fénysebességű terjedés miatt a kölcsönhatási bozon nem lehet nyugalomban. A fotontól eltérően mégis jogunk van tömegről beszélni, mert a W bozon energiája és az ennek megfelelő E/c² tömege a tér egy szűk tartományára lokalizálódik. (Itt érdemes utalni rá, hogy a W és Z bozonoknak nem a tömegét, hanem az energiáját lehet mérni a nagy energiájú proton-proton ütközések során képződő részecskék detektálásával). A W bozon fokozatosan csökkenő körfrekvenciája teszi lehetővé, hogy a részecske átalakítás „csavarkulcsa” legyen, mert rezonanciába léphet a különböző tömegű – azaz forgási frekvenciájú – részecskékkel.

3. 6. Impulzus szerepe az átalakulásban

A gyenge kölcsönhatások által vezérelt átalakulások mellékterméke a neutrínó, amit a folyamat „hulladék anyagának” tekinthetünk. Szerepük kettős, egyrészt az impulzus, másrészt az impulzusnyomaték megmaradási törvényének tesznek eleget. Ez előbbi szempontjából fontos, hogy noha a neutrínónak nincs tömege, impulzusa mégis van. A gyenge kölcsönhatás által előidézett átalakulás első lépésében, amikor a W bozonnal együtt egy neutrínó is kilép, a két részecske impulzusának összege nulla, azaz a neutrínó a W bozon meglökésével tesz szert impulzusra. Mivel fénysebességű mozgásról beszélünk, ez a saját impulzus a pc = E összefüggésből határozható meg, hasonlóan a fotonhoz. Az impulzus viszont irányfüggő mennyiség, ezért a meglökött W bozon mozgásának kitüntetett iránya lesz. Ez a polarizációs irány játszik fontos szerepet az átalakítási folyamat második lépésében. Ez a lépés az első fordítottja, ekkor a W^– bozon átalakul elektronná egy második neutrínó kibocsátása mellett, de ez már jóval kisebb energiával történik, mert a spirálmozgás során a körfrekvencia lecsökkent. De mekkora ez a csökkenés? Nézzük meg a forgás fázisának változását, amit a frekvencia változása miatt integrálással határozhatunk meg:

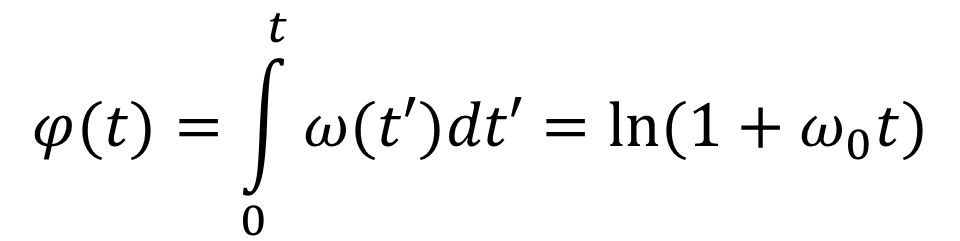
A fázis változását a sugár függvényében logaritmikus skálán mutatja a 6. ábra.

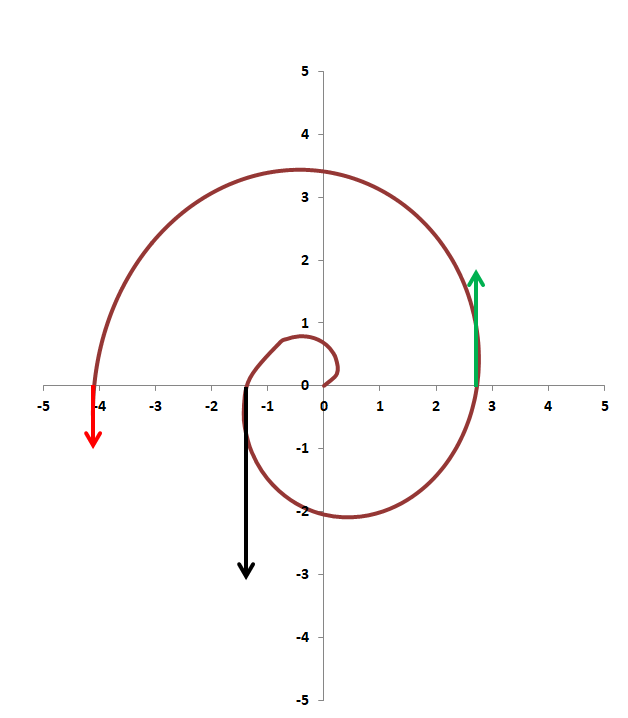
ábra. A W bozon spirális pályája logaritmikus ábrázolásban, a vastag nyíl az eredeti polarizációs irány, a fekete a tau, a zöld a müon, a piros az elektronkilépés irányát mutatja

6. 7. A W bozon aktív fázisai

A következő kérdés, hogy a spirálmozgás milyen fázisánál következik be a második lépés, amikor képződik a két lepton? A spirálmozgás során fokozatosan csökken a W bozon energiája, ami végbemehet, mert a tér görbülete – és így a kiegyenlítő negatív potenciális energia – evvel együtt csökken. A W bozon azonban nyomtalanul nem tűnhet el, mert ekkor sérülne az impulzusnyomaték és a töltés megmaradási törvénye. Létezik azonban három „kijárat”, amikor képződik a két lepton, felhasználva a töltést és az impulzusnyomatékot is. Ezt a kijáratot a W bozon kezdő iránya szabja meg: akkor jön létre átalakulás, amikor egy-egy félfordulat végbemegy, ugyanis ekkor az impulzus újra az eredeti iránnyal lesz párhuzamos. Ennek megfelelően bármelyik π szögű elfordulásnál létrejöhet a két lepton. Vezessük be a ρ = 1 + ω₀t tömegcsökkenési arányt, amely π szögű elfordulásnál e^π = 23,14 nagyságú lesz. Ez azt jelenti, hogy amikor az eredeti tömeg ilyen mértékben csökken, bekövetkezhet a W bozon átalakulása. Ezt is szemlélteti a fenti ábra. A W bozon induló energiája E₀ = 80,395 GeV a mérések szerint, ez lecsökken az első félfordulat után E_π = 3,4738 GeV, a másodiknál E_2π = 150,1 MeV, a harmadiknál E_3π = 6,487 MeV értékre. Ezen az energián osztozik a létrejövő két fermion. Rendeljük a tau, müon és elektron, valamint a megfelelő neutrínókhoz az n = 1, 2, 3 kvantumszámot, az előbbieknél az m_n nyugalmi tömegből, az utóbbiaknál a p_n saját impulzusból számíthatjuk ki az energiát:

E_nπ = m_nc² + p_nc

Az összefüggés lehetőséget ad, hogy a neutrínók három típusának megbecsüljük sajátenergiáját, feltételezve, hogy az elektron típusú részecskék kinetikus energiája elhanyagolható. A W bozon eltűnése után visszaáll az eredeti energia (helyreáll az energiamegmaradás szokásos törvénye, amely nem veszi számításba a tér potenciális energiáját), ezért az határozza meg, milyen részecske szabadul ki a W bozonból, hogy melyik saját energiája van közel a félfordulatok E_nπ értékéhez. Mivel a tau részecske energiája 1,77682 GeV, azaz E_π fele, így ez a részecske a W bozon első félfordulatánál jöhet létre, ekkor a tau neutrínóra jutó energia maximum 1,697 GeV lehet, tehát a két képződő részecske közel egyformán osztozik a bozon E_π energiáján. A müon saját energiája 105,658 MeV, ezért ez már egy teljes fordulat után jön létre, a müon neutrínóra jutó energia pedig 44,44 MeV lesz, tehát kisebb, mint a müon saját energiája. Végül az elektron, melynek sajátenergiája 0,511 MeV, a harmadik félfordulat után jön létre, és ekkor a neutrínóra jut a W bozon maradék energiájának nagyobb hányada: 5,976 MeV. A nagyságrendi változásból látható, hogy a tau, müon és elektron tömege azonos ütemben csökken a W bozon félfordulatainak energiaveszteségével. A harmadik félfordulat a W bozon utolsó „kijárata”, mert az elektron stabilis részecske és spontán módon nem bocsát ki újabb W bozont.

3. 8. Hadronok bomlása

Leptonok bomlásánál lényegesen bonyolultabb a kvarkokból felépülő mezonok (kvark + antikvark) és a barionok (három kvark, vagy három antikvark) bomlási mechanizmusa. Ennek egyrészt azaz oka, hogy a kvarkok a hadronok belsejében nincsenek sem tömeg, sem impulzus sajátállapotban, amelyben jól definiált sajátértékkel rendelkeznének, másrészt az összetett hadronokban (ez a barionok és mezonok összefoglaló neve) az erős és az elektromágneses kölcsönhatás is fontos szerepet játszik a gyenge-kölcsönhatás mellett. A kvarkoknak két típusa van a 2/3e töltésű u, és a –1/3e töltésű d, és a leptonokhoz hasonlóan három generációjuk létezik, melyek csak a tömegükben különböznek (pontosabban a renormált tömegükben, mert szabad kvark nem figyelhető meg). Az u típus két magasabb generációja a c és a t kvark, a d típusé az s és a b nevű kvark. A kvarkok három generációjának renormált tömege nagyságrendileg igazodik a W bozon három aktív állapotához: u és d az E_3π, c és s az E_2π, míg b az E_π energiával összemérhető nagyságú. Kilóg a sorból a t kvark, amelynek nagy tömege meghaladja a W bozonét, evvel függhet össze, hogy olyan hadron nem is létezik, amelynek t kvark lenne az egyik összetevője.

3. 9. Béta-bomlás

Hadronok közül az számít kivételnek, amelyben a gyenge kölcsönhatás hozza létre a bomlást, ennek oka, hogy az elektromágnesesség által előidézett bomlás ennél 10 nagyságrenddel gyorsabb. Ezért amikor a két kölcsönhatás együtt játszik szerepet, a gyenge kölcsönhatás részesedése nem becsülhető meg. Barionok közül a két nukleon (proton és neutron) különösen stabil: a proton (uud) spontán módon nem is bomlik fel, csak neutrínó-, vagy gamma-sugárzással alakítható át, míg a neutron (udd) bomlásának felezési ideje rendkívül hosszú: 880 s. A proton stabilitását az okozza, hogy a barionok közül ez a legkisebb saját energiával rendelkező részecske, neutron pedig azért stabilis, mert az elektromágneses kölcsönhatás nem idéz elő spontán bomlást. Ennek oka, hogy a gamma-sugarak nem rendelkeznek töltéssel, és így más részecskék töltését sem változtathatják meg, legfeljebb részecske-antirészecske párokat hozhatnak létre, ha elég nagy az energiájuk. A neutron spontán béta-bomlásakor proton jön létre, amelyet elektron és (anti)neutrínó kibocsátása kísér, magasabb generációhoz tartozó fermionok nem léphetnek ki, mert a neutron és proton közötti 1,3 MeV energiakülönbség nem elegendő müonok létrehozásához. Bár a képződő W bozon tömege elég nagy, de mindig úgy bomlik, hogy utána a szokásos energiamegmaradási törvény újra érvényes lesz.  A béta-bomlás tehát kvark-kvark átalakítási folyamat W^– bozon közvetítésével:

u → d + W^–→ d + e^– + ν_e

3. 10. Mezonok bomlása

A mezonok családjában az ud összetételű (az aláhúzás jelöli az antikvarkot), +e töltésű pion a legstabilabb, melynek tömege 139,6 MeV/c², a legkisebb a mezonok közül. Ez a tömeg egyrészt összemérhető a W bozon E_2π energiájával, másrészt nagyobb a müon tömegénél, ami magyarázza a kvark kombináció átalakulását müonra és neutrínóra:

ud → W⁺ → μ⁺ + ν

Ekkor a gyenge-kölcsönhatás a kvark-antikvark kombinációt alakítja át leptonokra. Hasonló bomlási folyamata van az us összetételű +e töltésű kaonnak is, ahol a 493 MeV sajátenergia szintén elegendő müon részecske generálásához.

A gyenge kölcsönhatás által generált átalakításoknak csak egy részére tértünk ki. A Standard Modellben vizsgált nagyszámú átalakulásnak vannak egyéb kiválasztási szabályai is, ami további kvantumszámok megmaradásához kapcsolódik (gyenge izospin, gyenge hipertöltés). A komplex forgásállapotok játékszabályainak ismertetésére más alkalommal kerül majd sor.

3. 11. A W bozonokat generáló Euler-erő

Az Euler tehetetlenségi erőről korábban már volt szó, amely fontos szerepet játszik a fermionokból kilépő forgások képződésében. Ennek forrása a fermionokat alkotó térforgás megszűnése a részecskék határánál. Ez a határ azonban nem lehet egyetlen matematikai pont, mert akkor végtelenül nagy lenne az Euler-erő. Véges szélességű héj létezése a kvantummechanikai bizonytalansági elv speciális következményének is tekinthető: a sugár R hosszának bizonytalansága a részecske p impulzusának végességéhez kapcsolódik a pxr = ħ összefüggés miatt.

 Az Euler-erő a forgómozgás érintőjének irányába mutat, összhangban avval a képpel, hogy a képződő egytengelyes forgáshoz kapcsolódó haladó mozgás – ellentétben a fotonnal, ahol a haladási irány párhuzamos a tengellyel – ekkor a forgás síkjában lesz.

Az erő nagyságát az határozza meg, hogy mekkora annak a tartománynak a szélessége, ami alatt a részecske M tömegét meghatározó forgási frekvencia nullára csökken le. Az innen számolható Euler-erő a fénysebességű forgás modellben:

F_Euler = ħc/RΔR

Itt ΔR a fermionok héjvastagságát jelöli, ami természetesen jóval kisebb, mint a részecske R = ħ/Mc  Compton-sugara. Abból a tényből, hogy valamennyi részecskeátalakulási folyamatban ugyanakkora tömegű W bozon jön létre, arra kell következtetni, hogy fermionokban a gyenge kölcsönhatást generáló Euler erő azonos, vagyis minden fermionban megegyezik a héjvastagság RΔR  keresztmetszete. Mivel az R Compton-sugár a tömeggel fordítva arányos, így a héjvastagság annál nagyobb, minél nagyobb a tömeg. A vastagság nem haladhatja meg a sugarat, ezért a gyenge kölcsönhatás kijelöl egy maximális tömeget. Ezért annak oka, hogy a mikrorészecskéknek nem lehet bármekkora tömege, visszavezethető a gyönge kölcsönhatása szétbontó szerepére. Úgy is fogalmazhatunk, hogy a térnek a görbülési képessége véges, mert egy határ fölött már nem tudja féken tartani az Euler-erőt. Vagyis a térnek a fénysebesség mellett létezik egy másik átléphetetlen határa is: a legkisebb görbületi sugár, amelynél kisebb tartományba már nem préselhető be fizikai objektum.   Ennek a határnak felel meg a W bozon tömege, ahonnan a R = ΔR egyenlőséget feltételezve kapjuk meg a részecskék minimális görbületi sugarát:

R_min = 2,456·10^-18 m

A 173 GeV/c² tömegű top kvark sugara ennél már kisebb lenne, ami magyarázza, hogy nem figyelhető meg olyan hadron, amelyben a top kvark is jelen lenne.

A kis héjvastagságból fakadó nagy Euler-erő azt is magyarázza, hogyan tudnak a W bozonnál jóval kisebb tömegű fermionok kibocsátani náluk több nagyságrenddel nehezebb kölcsönhatási bozont. Összehasonlítva a héjvastagságot az elektron Compton-sugarával, ez 157 330-szor kisebb, míg müonnál az arány 761 és a tau részecskénél 45,25. Az elektron stabilis részecske, a müon és tau elbomlik W bozonná és egy neutrínóvá

2,2·10^-6, illetve 2,9·10^-13 s alatt. Ebből arra következtethetünk, hogy a héjvastagság és a Compton-sugár aránya exponenciálisan változtatja meg a fermionok stabilitását, és elektron esetén az élettartam akár az univerzum korát is elérheti.

3. 12. A Z bozon színre lépése

A gyenge kölcsönhatás olyankor is megfigyelhető, amikor nem történik részecskeátalakulás. Buborékkamrában vizsgált elektronoknál azt tapasztalták, ha jelentős neutrínó fluxus halad át a kamrán, egyes elektronok mozgása hirtelen megváltozik (Carlo Rubbia, Simon van der Meer, Nobel díj: 1984). Ezt úgy lehetett értelmezni, hogy az elektron lökést kaphat a neutrínóktól, amit viszont csak egy új kölcsönhatás idézhet elő, hiszen gammasugarak nem voltak jelen. Itt arra kell gondolni, hogyan tudja az egyik test meglökni a másikat, amikor nekiütközik? Számunkra ez természetesnek tűnik, pedig ez a lökés nem jöhetne létre elektromágneses kölcsönhatás nélkül! A neutrínó például nem rendelkezik elektromos töltéssel, ezért bár óriási számban áramlanak a Napból, hatásukat nem vesszük észre, gyakorlatilag veszteség nélkül haladnak át az egész Földgolyón! A neutrínó sugárzás során meglökött elektronok töltése változatlan marad, ami töltéssel nem rendelkező bozon jelenlétére utal, ez a részecske zéró töltése miatt a Z bozon nevet kapta. A szakirodalom a folyamatot rugalmas neutrínó szórásnak nevezi, amely az jelzi, hogy a folyamatban nem alakul át a meglökött elektron más részecskévé.

A fénysebességű forgásmodell úgy értelmezi a Z bozont, mint két ellentétes kiralitású spirálmozgás szuperpozícióját. A W bozonhoz hasonlóan a semleges Z bozon tömegénél fogva impulzussal rendelkezik, és ezt ütközéskor átadhatja elektronoknak a gyenge kölcsönhatás révén.

A kísérletek során meghatározták a Z bozon tömegét, amit 91,2 GeV/c² nagyságúnak találták, ez meghaladja még a W bozon tömegét is. Ez úgy értelmezhető, hogy a semleges neutrínók héjvastagsága valamivel kisebb a töltéssel rendelkező fermionokhoz képest. Vagyis a tér minimális görbületi sugara lecsökken semleges töltésű részecskék formálódása esetén:

R_min = 2,165·10^-18 m

3. 13. Higgs bozon és a fénysebességű forgások

Higgs koncepciója is új szerepet ad a térnek, amelynek szimmetriatörésére vezeti vissza az ősi részecske színrelépését, amelynek bomlástermékei hozzák létre a fermionok és bozonok tömegét. Ezt a részecskét nevezzük ma Higgs bozonnak, és az a mező, amely ezt megteremti a Higgs mező. Ennek a részecskének nincs töltése és spinje sem, emiatt fénysebességű forgások sem tartoznak hozzá. Viszont ez a részecske teremti meg az előfeltételét, hogy ebből a szimmetriatörésből kialakuljanak a fénysebességű forgások, azaz a fermionok és a spinnel rendelkező kölcsönhatási bozonok. Az LHC kísérletek egyértelműen bizonyították, hogy létezik egy 127 GeV energiájú részecske, ami megfelel azoknak a tulajdonságoknak, amit a Higgs bozonnak teljesíteni kell. Tömege elég nagy ahhoz, hogy kisarjadjanak belőle a W és a Z bozonok, majd ezek bomlásaiból az elemi részecskék teljes világa. Mivel a Higgs bozont nem fénysebességű forgások alkotják meg, így nem vonatkozik rá a szabály, amely behatárolja a maximális részecske tömeget.  A Higgs bozon létezését alátámasztó kísérletek így egyúttal a fénysebességű forgás koncepciójának is bizonyítékai.

3. 15. Lépés a kölcsönhatások egyesített mezőelmélete felé

A mezőelméletek, tehát a kvantumelektrodinamika és annak gyenge kölcsönhatással egyesített változata az elektrogyenge kölcsönhatás elmélete, valamint a kvantumkromodinamika (ez írja le az erős kölcsönhatást), egységes keretek között tárgyalja a három kölcsönhatást: az elektromágneses, a gyenge és az erős kölcsönhatást. Viszont hosszú ideje tartó elméleti erőfeszítések ellenére sem sikerült a képbe beilleszteni a gravitációt. Ennek a feloldására tesz kísérletet a fénysebességű forgások koncepciója. A kölcsönhatások véges sebességgel terjednek, ez a fénysebesség, amelynek magyarázata fénysebességű közvetítő folyamatokat igényel. A gravitáció kivételével a közvetítést az S = 1 spinű bozonok végzik el, melyeket a fénysebességű modell egytengelyű forgásokként ír le. Ebben a fénysebesség a kulcsszereplő a kvantum létrehozásával. Az első részben leírtak szerint a gravitációnak is van közvetítője, a kéttengelyű és a távolsággal csökkenő frekvenciájú S = 0 spinű forgáskombináció, amelyhez nem tartozik kvantum. Ha kiterjesztjük a részecskefogalmat, ezt a mozgást is felfoghatjuk részecskének, amely csak virtuálisan létezik, és szerepe, hogy felépítse a tér gravitációs görbületi struktúráját.

A fénysebességű forgásmodell csak egy lépést tesz a végső egységesített elmélet megalkotása felé. A megoldandó feladatot az okozza, hogy a Standard Modell valójában nem több, mint egy adatgyűjtemény, ugyanis hiányzik belőle az elméleti keret, amelyből le tudnánk vezetni a mért adatok hosszú sorát. Példaként vegyük az elektron, a müon és a tau részecskék tömegarányát. Olyan elméletre lenne szükség, mint ami az atomokban meghatározza az egyes elektronpályák diszkrét energiáját. Ennek alapja a fotonok szabályozó szerepe, amely kijelöli az elérhető energiaszinteket, amit az elektronpályák impulzusnyomatékához kapcsol. Ennek mintájára képzelhetjük el, hogy a fénysebességű kettős forgások közül az elektron képviseli az alapállapotot, a müon és tau részecske pedig gerjesztett állapotnak felel meg, ahol a gerjesztési frekvenciákat a gyenge-kölcsönhatás határozza meg a W bozon által. Ez persze bonyolultabb folyamat, mint ami meghatározza az elektronok energiáját az atomokban, mert a bozon mellett egy másik részecske is szerepet játszik a gyenge kölcsönhatásban, mégpedig a neutrínó. Bár a fénysebességű forgásokra alapozott modellel sikerült nagyságrendi magyarázatot adni a részecskék tömegarányára, de továbbra sincs meg az egzakt elmélet, amely pontos értékeket szolgáltatna. Ennek megtalálása még a jövő feladata.

ÖSSZEFOGLALÁS

A fénysebességű forgás mint szemléleti módszer

A fénysebességű forgás a fizika olyan szemléleti módszere, amely maximálisan támaszkodik a modern fizika eredményeire, a speciális és általános relativitáselméletre, a kvantummechanikai mezőelméletekre és a részecskefizikára. Segít megérteni a sokszor nehéz matematikai eszközökkel dolgozó elméleteket, szemléletessé téve azokat. Új megvilágításba helyez fizikai fogalmakat, mindenekelőtt a fizikai teret, amit az anyagi világ aktív szereplőjének tekint, amely önmozgásaival hozza létre a részecskéket. A tér új szerepére épül Higgs koncepciója is, amikor a részecskék és a tömeg keletkezését a tér szimmetriatörésére vezeti vissza, amely maga nem fénysebességű forgás, hanem annak előfeltétele. A fénysebességű forgás új értelmezést ad a tömeg, az elektromos és színtöltés eredetére, és kapcsolatot teremt a fizika különböző területei között. Néhány esetben egyszerűbb számítási módszert kínál fizikai állandók meghatározására, azáltal, hogy szerves kapcsolatot épít ki a kvantummechanikai és a klasszikus fizikai látásmód között. A koncepció segítségével ki lehet küszöbölni néhány paradoxont is, amibe a modern fizika beleütközött.

Mindazonáltal a fénysebességű forgások koncepciója nem teszi fölöslegessé a mezőelméleti és a részecskefizikai módszerek alkalmazását, viszont segíti azok befogadását, amikor új megvilágításba helyezi az alapfogalmakat, és kapcsolatot épít ki a józanész világával. A fénysebességű forgások koncepciója segít abban is, hogy egy lépéssel közelebb juthassunk a négy alapvető fizikai erő közös elméletének megtalálásához. Összeköti a gravitációt és az elektromágnesességet azáltal, hogy mindkettőt a fermionból kiáradó virtuális forgásokra vezeti vissza, viszont amíg a gravitációt közvetítő kettős forgás nem fénysebességű mozgás, addig a fotonoknál az egytengelyű forgások fénysebességgel mennek végbe. A gyenge kölcsönhatást az köti össze az elektromágnesességgel, hogy mindkettő egy forgás és egy haladó mozgás kombinációja, csak az előbbinél a haladási irány merőleges, az utóbbinál párhuzamosa forgástengellyel. Az erős kölcsönhatás annyiban hasonlít az elektromágnesességhez, hogy a másodlagos mozgás iránya párhuzamos a forgástengellyel, de az erős kölcsönhatásnál ez a mozgás nem előrehaladás, hanem oszcilláció. Az erős gravitáció fénysebességű kettős forgásai alkotják meg a fermionokat a térben, azáltal, hogy extrém görbületet hoznak létre, amelynek potenciális energiája kiegyenlíti a centrifugális erőt. Az így képződő fermionok kerülnek egymással kölcsönhatásba a gravitációs és elektromágneses erők, valamint az erős kölcsönhatás révén. Végül a gyenge kölcsönhatás gondoskodik arról, hogy a különböző fermionok átalakulhassanak egymásba, és megszabja a végső határt a tér maximális görbületére, azaz a részecskék maximális tömegére.

Az einsteini gondolat szerint a gravitáció ekvivalens a gyorsulással együtt járó tehetetlenségi erővel. Ezt a gondolatot viszi tovább a fénysebességű forgások koncepciója, amikor a többi kölcsönhatást is kapcsolatba hozza a forgó rendszerek tehetetlenségi erőivel, jelesül a Coriolis, a centrifugális és az Euler-erővel. A kiterjesztett ekvivalencia elv révén közelebb kerülhetünk a régóta keresett célhoz, hogy megtaláljuk a kölcsönhatások egyesített mezőelméletét.

A blog további írásai elérhetők: „Paradigmaváltás a fizikában”

Az einsteini gondolat szerint a gravitáció ekvivalens a gyorsulással együtt járó tehetetlenségi erővel. Ezt a gondolatot viszi tovább a fénysebességű forgások koncepciója, amikor a többi kölcsönhatást is kapcsolatba hozza a forgó rendszerek tehetetlenségi erőivel, jelesül a Coriolis, a centrifugális és az Euler-erővel. A kiterjesztett ekvivalencia elv révén közelebb kerülhetünk a régóta keresett célhoz, hogy megtaláljuk a kölcsönhatások egyesített mezőelméletét.

A blog további írásai elérhetők: „Paradigmaváltás a fizikában”

2. Pillantás az elemi részecskék belsejébe: az erős-kölcsönhatás

Az első részben eljutottunk odáig, hogy alapvető kapcsolatot találtunk az elektromágnesesség és a gravitáció között: amíg az elektromágnesességet az egytengelyű fénysebességű forgások, azaz a fotonok közvetítik, addig a gravitációt spinnel nem rendelkező kettős forgások hozzák létre. A potenciálteret virtuális forgások építik fel a fermionokból kilépve és elnyelődve, de amíg a fotonok a fénysebességű forgások révén impulzusnyomatékkal és így kvantummal rendelkeznek, ez a tulajdonság hiányzik a kilépés után a távolsággal lassuló kettős forgásokból. A második részben tovább lépünk az erős kölcsönhatások birodalmába, és feltesszük a kérdést, vajon a fénysebességű forgások alkalmasak-e arra, hogy választ adjanak az erős kölcsönhatás által feltett kérdésekre, mindenekelőtt megtudjuk-e magyarázni, hogy miért rendelkeznek a kvarkok törttöltésekkel és mi a szín-kvantumszám eredete, amelyet az erős kölcsönhatás közvetítői, a gluonok alakítanak ki.

Ez a fejezet jelentős részben a „Pillantás az elemi részecskék belsejébe: kvarkok és gluonok különös világa” című korábbi íráson alapul.

2. 1. A Kvarkok mozgásformái és a húrrezgések

Közelebb juthatunk a kvarkok és gluonok különleges tulajdonságainak megértéséhez, ha valamilyen geometriai alakzathoz tudjuk kötni mozgásukat és szerkezetüket. A kvarkok fermion típusú elemi részecskék és spinjük S = ½. Evvel szemben a kölcsönhatásokat közvetítő elemi bozonok spinje S = 1, ami egyaránt vonatkozik az előzőekben tárgyalt elektromágneses kölcsönhatást közvetítő fotonokra, a következő részben ismertetésre kerülő gyenge kölcsönhatás W és Z bozonjaira, valamint a mostani rész tárgyául szolgáló erős kölcsönhatáshoz rendelt gluonokra. A fénysebességű forgás koncepciója szerint a fermionok és bozonok tulajdonságai a részecskéket alkotó forgások szimmetriájára vezethetők vissza. Az S = 1 spinhez a tér lokális egytengelyű forgása tartozik, szemben az S = ½ spinű fermionokkal, ahol két egymásra merőleges tengely körül történik a forgás.

Hogyan értelmezhetjük fénysebességű forgásokkal a kvarkok törttöltését, és két alaptípusának (flavour): up (röviden u) és down (d) létezését. Miért lépnek fel épp harmadok a töltésekben: ±2/3e és ±1/3e, és miért épp három kvark alkotja a barionokat? Arra könnyebb válaszolni, hogy a leptonoknál és kvarkoknál miért létezik három generáció: ez értelmezhető a fénysebességű forgások generációnként növekvő frekvenciájával. A Standard Modell szerint a második generációban charm (c) és strange (s), a harmadikban top (t) és bottom (b) tartozik ugyanabba a típusba, mint az up és down kvark.

A forgásmodell felépítéséhez analógiát nyújtanak a húr rezgései. A két végén rögzített húr alaprezgése a fél hullám, de létrejönnek felharmonikusak is: egész hullám, másfél hullám stb. Erre rímelnek a kvantummechanikában a molekulavibrációk, ahol a vegyértékrezgéseket az n = 0, 1, 2 … kvantumszám jellemzi. Az n = 0 típusú oszcilláció feleltethető meg a húr alaprezgésének, amit zérusponti rezgésnek is neveznek, mert még alapállapotban se áll le az összekapcsolt atomok mozgása, és ezáltal megnövekszik a molekula energiája is. Ez eltér a kifeszített húrtól, amelyik nyugalomban van, amíg nem pendítjük meg. Az alapállapotú vegyértékrezgés térbeli eloszlásának egy maximuma van és nincs csomópontja, ebben a húr fél hullámához hasonlít. A gerjesztett n =1 molekularezgés viszont már két maximummal és egy csomóponttal, az n = 2 pedig 3 maximummal és 2 csomóponttal rendelkezik, akárcsak a húrrezgés felharmonikusai. 

2. ábra. A rezgő húr három alap harmonikusa

3. ábra. A kvantummechanikai oszcillátor pozíciójának valószínűségi eloszlása a kitérés függvényében, a görbék közül a fekete: n = 0, a kék n = 1, a piros n = 2, a zöld n = 3 kvantumszámhoz tartozik

2.2 . Oszcilláló forgások hármas szerkezete

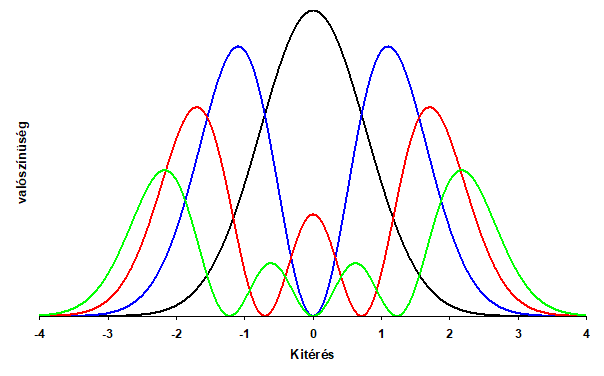
Beszélhetünk-e hasonló gerjesztett állapotokról, ha nem oszcillációról, hanem forgásokról van szó? A rezgés és forgás kapcsolatba hozható, hiszen ha a forgómozgást az átmérőre vetítjük, akkor oszcillációkat kapunk. Azt kell tehát keresnünk, hogy milyen szerkezetű forgás vetülete felel meg az egyes n = 0, 1, 2 oszcillációknak?  Induljunk ki az egyszerű forgásból, amely folyamatosan körbeszalad! Itt a forgás vetületének közepén fellép egy maximum és nincs csomópont, akárcsak a húr fél hulláma esetén, vagy az n = 0 oszcillációnál. De bontsuk fel a körbejárást részforgásokra (hurkokra), mégpedig oly módon, hogy a mozgás során csomópontok, illetve maximumhelyek alakuljanak ki! Ehhez az kell, hogy az első részforgás félúton lépjen át egy másodikba, ami úgy valósulhat meg, ha az új hurok forgásiránya fordítottja lesz az előzőnek. Például, ha az első részforgás iránya megegyezik az óramutató járásával – jelöljük ezt „+” szimbólummal – akkor a második hurok mozgása már szembe megy az óra járásirányával, amit a „– ” szimbólummal jelölhetünk. Ez viszont azt jelenti, hogy a második részforgás félfordulat megtétele után szembemegy az alapforgással (lásd 4. ábra). Ilyen kételemű „+–” felbontás ezért nem lehetséges. Ki kell tehát zárni a lehetőségek közül a két részforgásból álló és egy csomópontos összetett forgásokat. Viszont, ha a második részforgás átmegy egy harmadikba, akkor a forgáskombináció a félfordulat után egyirányú lesz az alapforgással. Ebből az elvből következik, hogy az összetett forgásban csak páratlan számú hurok lehet, melyek közül a legegyszerűbb a háromhurkos „+–+” felbontás, amelyben két csomópont és három maximumhely található. A csomópontokat tartalmazó forgás koncepciója tehát összhangban van a barion típusú részecskék hármas szerkezetével. (Lehetne még 5 hurkos összetett forgás is, de erre csak akkor lenne szükség, ha a részecskék Standard Modelljében lennének 5 részecskéből álló barionok is.) Leptonokhoz (elektron, pozitron, neutrínó) képest az a döntő különbség, hogy a kvarkoknál nem ekvivalens a két forgás, és ez az aszimmetria új típusú kölcsönhatásokhoz vezet.

4. ábra. Balra: két hurokra, jobbra: három hurokra bontott forgás körüljárási iránya az egyszerű forgáshoz képest. A kéthurkos bontásban a félfordulat piros nyila fordított a feketéhez képest, míg a háromhurkosban megegyezek az irányok.

2. 3. Miért rendelkeznek a kvarkok törttöltésekkel?

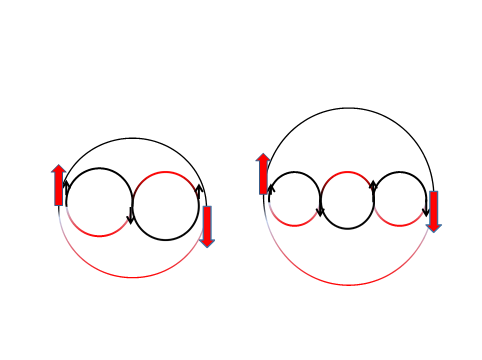
Térjünk most rá a törttöltés eredetére! Az S = ½ spinű fermionokat kettős forgások hozzák létre, melyben nevezzük az egyik forgást X-nek, a másikat Y-nak. Csak a második, azaz Y forgás legyen összetett. A 4. ábrán a hurkokra bontást síkban ábrázoltuk, itt azonban az egyes hurkok síkja eltérő, mégpedig egymásra merőleges (Lásd 5. ábra).

5. ábra. Baloldalon az xyx, jobboldalon az yxy típusú oszcillációs forgások láthatók, lent pedig a vetületek

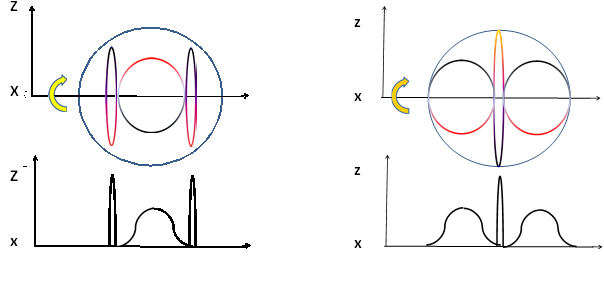
Ez a geometria már értelmezi a törttöltéseket, mégpedig azáltal, hogy az Y forgás felbontásában szereplő egyes hurkok forgástengelye részben párhuzamos az X forgáséval (ekkor nincs Coriolis-erő), részben viszont merőleges X-re (ekkor van Coriolis-erő), és jelölje az előbbi tengelyt x, az utóbbit y. Ez a felbontás nem változtatja meg az S = ½ spint, vagyis az impulzusnyomatékot, mert a mozgás iránya végig merőleges marad a sugárra egyezően az egyszerű körforgással.

Két lehetséges forgáskombináció jöhet létre: (xyx), illetve (yxy), amit a fenti ábra mutat be. Az y hurkok száma adja ki a töltést, mert csak ott lép fel Coriolis erő, viszont ennek előjele a körüljárási iránytól, azaz a kiralitástól függ. Jelöljük „+” és „–” szimbólumokkal a körüljárási irányt, evvel négy forgáskombinációhoz jutunk: (x⁺y^–x⁺), (x^–y⁺x^–), (y⁺x^–y⁺) és (y^–x⁺y^–). Az egyes forgáskombinációk töltésének nagysága -1/3e, +1/3e, +2/3e és -2/3e lesz, megfelelve a d kvarknak és antikvarknak, illetve az u kvarknak és antikvarknak. Az összetett Y forgás körüljárási iránya azonos az első részforgás előjelével, és ennek megfelelően az Y⁺ és Y^– forgások reprezentálják a részecske és antirészecske kettősséget. Ugyanezt úgy is jelölhetjük, hogy felcseréljük az egyszerű X és az összetett Y forgások szerepét, amit YX típusnak nevezhetünk. Ekkor az Y forgás lesz az egyszerű, és az X forgás az összetett, és az XY, illetve YX kombinációk kvarkot, illetve antikvarkot jelölnek.

.

2. 4. Oszcillációk kötött rendszerekben

Kvarkokra javasolt mozgásformát oszcillációs forgásnak is nevezhetjük, mert az Y forgás három hurkának z-irányú kitérései oszcillációt alkotnak. A kvark oszcilláció összhangban van a kvantummechanika már említett törvényével, miszerint minden kötött rendszer zérusponti rezgés végez, azaz még alapállapotban is van oszcilláció.

Az állítás meg is fordítható: csak akkor alakul ki oszcilláció két objektum kötött, ha valamilyen vonzó erőhatás összeköti őket. A kvarkokból felépülő barionokban és mezonokban az összetartó erőt az erős kölcsönhatás hozza létre, ezért a bezártság elv, mely szerint szabad kvark, azaz törttöltés megfigyelése nem lehetséges, összhangban van avval a felfogással, hogy a kvarkok létrejöttét oszcillációs forgások idézik elő: ha nincs oszcilláció, akkor kvark sincs. Úgy is fogalmazhatunk, hogy a törttöltésű kvark egy alacsonyabb szimmetriájú részállapot (mintázat) a magasabb szimmetriájú összetett struktúra (barion és mezon) belsejében, és a „mintázat” szerkezetét a részecskét egyben tartó erős kölcsönhatás határozza meg. Ez az erő alakítja ki az oszcillációs forgásokat, melyben a pályamozgás során megváltozik a forgástengelyek iránya is.

2. 5. Mi a kvarkok színtöltésének eredete?

A kvarkelmélet meghatározza, hogy a mezonok és barionok szerkezete milyen kvarkkombinációkból épül fel. Vizsgáljuk meg, a felépítési elv hogyan teljesül a kéttengelyű forgások modelljében. Nézzük először a barionokat, amelyek a Standard Modell szerint vagy három kvarkból, vagy három antikvarkból épülnek fel. A barionok spinje lehet ½, vagy 3/2, ez a lehetőség a spinek szokásos összeadási szabályából következik. Mivel a barionokban vagy csak kvarkok, vagy csak antikvarkok vannak, és az előbbi töltése 2/3e, vagy  –1/3e, az utóbbié 1/3e, vagy –2/3e, így belátható, hogy csak az elemi töltés egész számú többszöröse jöhet létre (nulla, ±e és ±2e), amikor három részecske kapcsolódik össze. A kvarkoknak a töltésen és spinen kívül van azonban egy további szabadsági fokuk is: a színtöltés. Ez három különböző értéket (színt) vehet fel, ugyanakkor a belőlük felépülő barionok szín semlegesek, azaz a bariont felépítő három kvark, vagy antikvark különböző színű, amelynek eredője „fehér” lesz. Eddig XY típusú kvarkokról beszéltünk, de ugyanilyen joggal választhatunk YZ és ZX forgásokat is, ahol mindig az első az egyszerű, a második az oszcillációs forgás. Ezt a három forgáskombinációt rendelhetjük a kvarkok három színéhez, viszont a barionok színsemlegessége („fehér színe”) azt követeli meg, hogy a három kvarkban, vagy antikvarkban az XY, YZ és ZX, illetve YX, ZY és XZ forgástípusok egyenlő súllyal szerepeljenek. Ez gömbszimmetrikus (izotrop szerkezetű) barionok esetén teljesül.

A barionok összetételének még eleget kell tenni a Pauli-elvnek is, amely megköveteli, hogy kötött kvantumállapotban ne forduljon elő két olyan fermion, melyek minden kvantumszáma egyezik. Ez azt jelenti, hogy nem lehet két kvarknak mind a töltése, mind a spin vetülete (+½ és –½), mind a szín-kvantumszáma és még generációs indexe is azonos. Három azonos kvarkból álló barion azonban létrejöhet, például az (uuu), vagy (ddd) konfigurációk, éppen a kvarkok különböző színére vonatkozó szabály miatt. Megjegyezzük még, hogy az atommagokat felépítő két nukleon, a proton és a neutron összetétele: (uud), illetve (udd).

A hadronok másik csoportját a mezonok alkotják, amelyek egy kvarkból és egy antikvarkból épülnek fel. Töltésük szintén csak az elemi töltés égésszámú többszöröse lehet, mégpedig 0 vagy ±e. A kvarkokra felírt töltéskonvenció itt is kizárja törttöltésű mezonok létezését. A spin lehet 0, vagy 1, megfelelően annak, hogy bozonokról van szó. A mezonoknak sincs színük, amit az biztosít, hogy az antikvarkok színe a kvarkok színének komplementere. Ez megkívánja, hogy az XY és YX kombinációk színe egymás kiegészítője legyen.

2. 6. Hogyan forrasztják össze a kvarkokat a gluonok?

A Standard Modell 8 független gluonnal értelmezi a kvarkokat összekötő erős kölcsönhatást. A gluon szintén bozon, és spinje S = 1. A fénysebességű forgás koncepciója szerint egytengelyű forgás alkotja a bozonokat, amelyet kiegészít a forgástengellyel párhuzamos másik mozgás is. Ez a párhuzamosság felel meg annak, hogy a gluonoknak a fotonokhoz hasonlóan nincs elektromos töltésük, a gluonok viszont rendelkeznek színtöltéssel. De milyen lehet ez a másik mozgás, amely létrehozza a színtöltést?

Nézzük először, hogyan is közvetíti az erőhatást a foton két töltött részecske között a kvantumelektrodinamika szerint? A töltött részecskék virtuális fotonokat bocsátanak ki (emisszió) és nyelnek el (abszorpció), melynek polaritását a részecske királis szimmetriája határozza meg. Ez a folyamat véletlenszerű fluktuációkat hoz létre a részecske pozíciójában (vákuum fluktuáció), de nem mozdítja el. Ha viszont a virtuális foton egy másik töltött részecskéhez eljut és elnyelődik, akkor vagy meglöki azt, (ha a két töltés előjele azonos), vagy a két részecskét egymás felé húzza (ha ellentétes a töltések előjele). Így jön létre taszítás, vagy vonzás. A virtuális gluonok hatása ettől annyiban különbözik, hogy a gluon a színtöltésen át közvetíti a kvarkok közötti vonzást függetlenül a kiralitástól. A gluon kiralitás függetlensége abban nyilvánul meg, hogy nincs elektromos töltése. Két kvark összekapcsolásához viszont két különböző szín tartozik: az egyik a kibocsátó kvark színe, a másik az abszorbeáló kvark színének komplementere (az abszorpció a szín komplementerét igényli). A kvarkok színét a kér forgás különböző szerkezetére vezethetjük vissza. Például az XY oszcillációs kettősforgást, azaz kvarkot „y⁺” színűnek nevezhetjük, mert y irányban oszcillál a Coriolis-erő, és pozitív indexet használunk, hiszen kvarkról és nem antikvarkról van szó. Evvel szemben az YX antikvarkhoz az „x^–” komplementer színt rendeljük hozzá, az x irányú oszcilláció miatt. A negatív index jelöli, hogy komplementer színeknél az oszcillációs fázis fordított. Ezt az elvet követve vezethetjük be a YZ és ZX kvarkok esetén az „z⁺” és „x⁺” színeket, míg a ZY és XZ antikvarkoknál az „y ^–” és „z ^–” komplementer színeket. Összesen tehát három alapszínről es három komplementer színről beszélhetünk.

Kvarkok esetén az oszcilláló forgás és az egyszerű forgás között fellépő Coriolis-erő bocsátja ki a gluonokat, de ez sokkal erősebb az elektromos erőnél, minthogy a kvarkok közvetlenül érintkeznek a barionokban és mezonokban. Emiatt az erős kölcsönhatásban nem csökken le a ħc szorzattal arányos erő, és így mintegy 137-szer nagyobb lesz a vonzóerő, mint amit az elektromágneses kölcsönhatás létrehozhat. A kölcsönhatás ereje nem változik a barionok mérettartományán belül, viszont az atommagokban, ha nem érintkeznek a nukleonok, a kontaktus hiányában a vonzás gyorsan megszűnik.

2. 7. Gluonok osztályozása a Standard Modellben

Az elmondottak értelmében a gluon tehát irányokat (azaz színeket) összekapcsoló közvetítő részecske, amely az egyik irányú oszcillációt átviszi egy másik irányba, és evvel járul hozzá, hogy a magas szimmetriájú barionokban és mezonokban kialakuljanak alacsonyabb szimmetriájú „mintázatok”, azaz a kvarkok. A gluon ezért elválaszthatatlan tartozéka a két kvarkkonfigurációnak: a háromelemű barionoknak és a kételemű mezonoknak. Sem kvarkokat, sem gluonokat nem észlelhetünk szabadon, ezek a részecskék csak együtt létezhetnek az összetett részecskéken belül. Ez nyilvánul meg abban is, hogy nem tudunk valódi tömeget rendelni az egyes kvarkokhoz, csak renormált tömegekről beszélhetünk, hiszen a részecskék saját energiáját a kvarkok és gluonok együttesen alakítják ki.

A barionok három különböző színű kvarkból, vagy antikvarkból épülnek fel, ennek megfelelően a „színváltoztató” gluonok a következők lesznek:

(x⁺y^–), (x⁺z^–), (y⁺x^–), (y⁺z^–), (z⁺x^–), (z⁺y^–)

Mezonokban viszont a részecske színsemlegességét iránytartó (színtartó) gluonok hozzák létre, melyekben nem változik meg az oszcillációs irány, tehát a szín-kvantumszám, ezek pedig a következők:

(x⁺x^–), (y⁺y^–) és (z⁺z^–)

A negatív indexek jelölik, hogy a komplementer színek oszcillációs fázisa ellentétes a színekhez képest.

A kilenc gluon 3*3-as mátrixba rendezhető:

(x⁺x^–)   (x⁺y^–)   (x⁺z^–)

(y⁺x^–)   (y⁺y^–)   (y⁺z^–)

(z⁺x^–)   (z⁺y^–)    (z⁺z^–)

Összességében gömbszimmetrikus potenciáltér jellemzi hadronokban az erős kölcsönhatást. Ennek megfelelően a háromdimenziós mátrix felbontható a forgáscsoport egy-, három- és ötdimenziós ábrázolására, hasonlóan az L = 0, L = 1 és L = 2 gömbfüggvényekhez. Az L = 0 gluon kombináció szingulett állapotnak felel meg, amelynek létezését a Standard Modell kizárja, emiatt beszél az elmélet nyolc független gluonról. A háromdimenziós L = 1 függvénytér vektoriális, az L = 2 ötdimenziós függvénytér tenzoriális erőmezőt hoz létre.

2. 8. Összetett részecskék spinje és véges hatáskeresztmetszete

A pontszerűséggel kapcsolatban érdemes még kitérni arra a kérdésre is, hogy a proton töltéseloszlása a mérések szerint nem pontszerű, bár az elektronhoz hasonlóan a spinje ½. Az elektron impulzusnyomatékát a fénysebességű kettős forgásra vezettük vissza, ezért ha evvel magyaráznánk a proton spinjét is, akkor nulla hatáskeresztmetszetet várnánk a szóráskísérletekben. Ha nem tudnánk az elméletből, hogy a proton három kvarkból épül fel, akkor már a véges hatáskeresztmetszet létezéséből levonhatnánk a tanulságot, hogy a proton összetett szerkezetű! Mivel a valóban elemi – tehát tovább nem osztható – fermionoknak a kettős forgás koncepciója szerint ½ a spinje, így a spinek összeadási szabályából már következik, hogy legalább három komponensből épül fel a proton, ugyanis két ½ spin összege nulla, vagy egy lehet. Egyébként az összetett részecskék családjában vannak két kvarkra bontható mezonok is, ahol tényleg a spin 0, vagy 1 értéket vesz fel. Három ½ spin alkothat akár ½, akár 3/2 spint is. Léteznek ennek megfelelően olyan barionok is, melyeknek spinje 3/2.

2. 9. Az atommagokat összetartó erő

Az atommagok felépítése további kérdést vet fel: milyen erő köti össze benne a nukleonokat, az (uud) szerkezetű protont és az (udd) neutront. Ez a kvarkokat összekötő erős kölcsönhatás másodlagos hatása, amit a kvantummechanika kicserélődési erőnek nevez. Ez akkor jön létre, ha két összetett objektum, például két atom a molekulában, vagy esetünkben a nukleonok az atommagban, egymás között felcserélik „alkatrészeiket”. A molekulák atomjaiban az elektronok, az atommagban a kvarkok „szabadon járnak-kelnek” a nukleonok között. Precízebben szólva az elektronok, illetve a kvarkok egyidejűleg több objektumban is megtalálhatók bizonyos valószínűséggel. Ez a kicserélődési kölcsönhatás, amely valamennyi fermion alaptulajdonsága, melynek szabályait a Pauli-féle kizárási elv adja meg. Molekulákban például ez az atomokat összekapcsoló kovalens kötés alapja. A kvarkok „átjárásához” a nukleonok közvetlen érintkezése szükséges, ami magyarázza, hogy miért olyan rövidtávú a nukleonokat összekötő vonzóerő.

2. 10. Áttekintés a kvarkok és gluonok világáról

Végül is, milyen képet alkossunk a gluonok és kvarkok világáról?  Képzeljük el úgy a hadronokat (a barionok és mezonok összefoglaló neve), amelyek kívülről gömbszimmetrikusok, de van egy belső szerkezetük is, amit kvarkoknak nevezünk. Mindegyik kvark egy-egy fénysebességű kettős forgás, melyekből az oszcilláló Coriolis-erők körforgásokat indítanak meg felületükön, és ezek összekötő rugóként kapcsolják egymáshoz a kvarkokat. Ezt nevezzük erős kölcsönhatásnak. A körforgások és oszcillációk összetett struktúrája alakítja ki a gluonok kettős színvilágát. Ez a színvilág a hadronon kívül már nem látszik, mert kifelé a hullámzás már gömbszimmetrikus pulzálást idéz elő, ami avval is együtt jár, hogy a hadronok töltése az elemi töltés egész számú többszöröse lesz. Törttöltésű részecske szabadon nem figyelhető meg, mert a gluonok építik ki azokat a több hurkos forgási állapotokat, amelyek megformálják a kvarkokat. A belső mozgásformák spontán módon képesek átrendeződni és kialakíthatnak újabb forgáskombinációkat, miközben kibocsátanak egyéb mozgásformákat is: elektronokat és neutrínókat. Ezeket az átalakulásokat a gyenge kölcsönhatás vezényli le, amivel majd a következő részben foglalkozunk.

Ennek a résznek fő mondanivalója, hogy fénysebességű kettős forgásokkal jól lehet szemléltetni az erős kölcsönhatás jelenségeit is.

Következő rész:

A blog további írásai: "Paradigmaváltás a fizikában"

„A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója” című könyvemben (Scolar kiadó, 2017) a modern fizika, mindenekelőtt a kvantummechanika elméletének bemutatására törekedtem, kiegészítve a fénysebességű forgások koncepciójával. Célom az volt, hogy a részecskefizika néhány rejtélyére magyarázatot találjak a tér fogalmának kiterjesztésével, amely nem csupán passzív tartály, amelyben a részecskevilág elhelyezkedik és végzi mozgásait, hanem megalkotja a részecskéket és meghatározza azok tulajdonságait: a tömeget, a töltést és a spint. Ennek megvalósítói a tér lokális tartományaiban fellépő eltérő szimmetriájú forgások, melyek véges kiterjedését a fénysebesség jelöli ki. Az elgondolás utat nyit a modern fizika néhány paradoxonjának feloldására, és közelebb vihet a fizika négy alapvető kölcsönhatásának – a gravitációs, elektromágneses, a gyenge és az erős kölcsönhatásának – egységes elmélete felé. A kiindulópont a relativitáselmélet által feltárt szingularitás, amely a látszólag semmiből anyagot teremt a fénysebesség által.

Vegyük sorra a részecskefizika különböző területeit, hogy lássuk a fénysebességű forgások szerepét az egyes fizikai jelenségek magyarázatában.

1.     A gravitáció és elektromágnesesség hasonlósága és eltérő sajátságai a fénysebességű forgások tükrében

Ez a fejezet jelentős mértékben támaszkodik „A pontszerű elektron legendájától a fénysebességű forgásokig” című bejegyzésre.

1.1 Az elektron pontszerűsége mellett szóló érvek

Pontszerű-e az elektron? Bizonyos kísérletek szerint igen! Erre adnak példát a Bhabha kísérletek. Bombázzunk elektronokat pozitronokkal! A találkozáskor a két részecske gamma sugárzás kíséretében annihilál. Könnyebb egy térben kiterjedt töltésrendszert eltalálni, ha annak nagy a mérete. A nagy energiájú szóráskísérletek azonban azt mutatják, hogy nagyon kicsi a találati valószínűség, és a mérési pontosság határain belül nulla az elektron töltéseloszlásának sugara. Más részecskéknél ez nem így van, így derítették fel különböző szórásvizsgálatokban a proton és neutron töltésének véges térbeli eloszlását.

Más jelenségekkel is összhangban van a pontszerűségi elv: az elektront ugyanis nem lehet kisebb egységekre felbontani. A felbonthatatlanság természetesen biztosan teljesül, ha tényleg pontszerű egy részecske, de ez önmagában még nem bizonyíték a pontszerűség mellett, mert a felbonthatatlanságnak más oka is lehet.

1.2.         Ellenérvek a pontszerűséggel szemben

Más oldalról, milyen érvek hozhatók fel a pontszerűség ellen? Mindenekelőtt feltehető a kérdés, hogy lehet-e bármilyen fizikai objektum végtelenül kicsi, felbontható-e az anyag végtelenül apró darabokra? Itt lép be a démokritoszi atomelv, amelynek álláspontja szerint, kell lenni valahol egy oszthatósági határnak, még ha mai tudásunk szerint ez a határ nem is az, amit ma atomnak nevezünk, sőt az atommag is felbontható nukleonokra (proton és neutron), de még ez sem a végső felbontási határ, hanem annak is vannak kisebb elemei: a kvarkok. Ismereteinket összegző Standard Modell szerint, a már tovább nem bontható elemi objektumok az említett kvarkok, de ide tartoznak még a fermionok közül az elektron és neutrínó család tagjai, valamint a különböző kölcsönhatásokat közvetítő bozonok, jelesül a fotonok, a W és Z részecskék, és a gluonok. A kérdés persze fennmarad, biztosak lehetünk-e abban, hogy amit ma a fizikai világ legapróbb építőköveinek tartunk, nem oszthatók-e mégis tovább, lehet, hogy ezek is valamilyen folytonos anyagból épülnek fel? Ha persze az elektron tényleg pontszerű, lezárhatjuk a kérdést, hiszen a pont az a végső matematikai határ, amely megfogalmazza a felbonthatatlan kiterjedés nélküliséget.

Ami azonban leginkább szembemegy a pontszerű elektron felfogásával, hogy az elektron olyan fizikai tulajdonságokkal rendelkezik, amely csak térben kiterjedt testeknek lehet: ezek a nyomatékot (momentumot) kifejező fizikai mennyiségek, jelesül az impulzus- és a mágneses nyomaték. Az előbbi arra utal, mintha az elektron tömege véges tértartományt foglalna el, az utóbbi szerint ez vonatkozik az elektron töltésére is.

1.3.         Az ellentmondás feloldása fénysebességű forgásokkal

Lehet-e egyáltalán olyan fizikai objektum, amely két ilyen egymásnak ellentmondó tulajdonsággal rendelkezik? Ha a részecskékhez fénysebességű forgásokat rendelünk, akkor igen! Ennek magyarázatát a relativitáselmélet Lorentz transzformációja adja meg. Ha hozzánk képest egy test valamilyen sebességgel mozog, annak méretét a mozgás irányában kisebbnek látjuk, és ha elérjük a fénysebességet, akkor a méret nullára zsugorodik. De ez csak a mozgás irányára igaz, mert a mozgásra merőlegesen a méret ugyanakkora marad. Képzeljünk el egy R sugarú köralakú objektumot, álló esetben a kerület hossza 2Rπ. Kisebbnek látja a külső szemlélő a kerület hosszát, ha forogni kezd a test ω = f/2π körfrekvenciával, és ha eléri a v = ωR kerületi sebesség a c fénysebességet, akkor a kör kerülete már nullára zsugorodik. De mi lesz a sugárral? Mivel a sugár mindig merőleges a mozgásirányra, ez változatlanul ugyanakkora marad. De lépjünk tovább és képzeljünk el egy olyan forgást, amelyik egyszerre két egymásra merőleges tengely körül megy végbe, ez már egy gömb felületét futja be. Ugyanis az első forgás által létrehozott kört, annak átmérője körül forgatva már kialakul a gömb. Kívülről nézve a gömb felülete már nullának látszik, ha a kerületi sebesség c, de sugarát továbbra is „láthatjuk”, ami alatt azt kell érteni, hogy amikor mérjük a gömbhöz tartozó nyomatékokat, annak nagysága arányos lesz a gömb sugarával, viszont hiába bombázzuk a gömböt kívülről, nem fogjuk annak felületét eltalálni. Persze, ha be tudnánk bújni a gömb belsejébe és avval együtt forognánk, a gömböt továbbra is szabályos gömbnek látnánk. Fénysebességgel mozgó rendszerekbe azonban nem tudunk belépni, ezért a fizikai törvényeket a külső megfigyelő szempontjából kell megfogalmazni.

1.     4.   Folytonosság, pontszerűség és diszkrét energiák

Hogyan kapcsolódik a részecskék pontszerűségének cáfolata a fizikai világ folytonosságának kérdéséhez? Az energia estén látszólag megszűnik a folytonosság, hiszen az atomban kötött elektronok diszkrét energiájúak, és adott frekvenciájú fény energiája is E = h·f nagyságú lépcsőkben változik. Fölvethető emiatt, vajon a tér és az idő se lenne folytonos? Nézzük először a klasszikus fizikát! Minden területen a folytonosságból indul ki, és differenciálegyenletekkel írja le törvényeit, akár mechanikáról, elektromágnesességről, vagy termodinamikáról van szó. Ez a szemléletmód abból indul ki, hogy – legalább is elvben – a mozgásokról folytonosan érkezik az információ a folytonosan érkező fény miatt. Gyakorlati szempontból ez a matematikai technika rendkívül hasznos, mert a végtelenül kis változások birodalmában lineárissá válnak a legbonyolultabb összefüggések is, ami nagyon megkönnyíti a számításokat. A bonyodalom az integrálásoknál következik be, amikor makroszkopikus méretekre terjesztjük ki a vizsgálatokat.

Jelenlegi kvantumfelfogásunk szerint sem beszélhetünk kvantált térről, vagy időről. Ennek oka, hogy a kvantummechanika operátorait az idő és a térkoordináták szerint differenciálhányadosok adják meg, már pedig ez megköveteli, hogy a koordinátákat végtelenül kis elemekre tudjuk felbontani, és folytonosnak kell lenni az állapotfüggvénynek is. De mégis hol az a pont, ami kvantumok kialakulásához vezet? Ez a körmozgás, amelyben a szögkoordináta 360 fokonként visszatér önmagába, ez az önmagába való visszatérés vetítődik ki az anyag hullámtermészetében is. Klasszikusan a mozgás pontról pontra követhető, mert elvben tetszésszerinti kis távolságban és időközben érkeznek hozzánk a fotonok, de ez már nincs így a kvantumok világában, mert a stacionárius állapotban „néma” az elektron, nem bocsát ki, vagy nyel el fotont, kizárólag csak a különböző állapotok közötti ugrásokat látjuk. Ha ebből visszakövetkeztetünk az elektronpályákra, az csak az egész pályáról, azaz a teljes körforgásokról adhat információt. Ez az információ a pálya impulzusnyomatéka, amit a redukált Planck-állandó egész számú többszöröse ad meg. Miért kötelező, hogy ez így legyen, miért nem keringhet tetszésszinti pályán az elektron? Ennek oka, hogy az elektron kötött pályára jutását a fotonok segítik elő. A szabadon mozgó elektronnak nincs pálya-impulzusnyomatéka, amikor azonban az atommag közelébe kerül, a vonzás gyorsítást, ez pedig foton kibocsátást okoz, de minden ilyen kibocsátás alkalmából ћ egységnyi impulzusnyomaték változás következik be. Végül, amikor kialakul a kötött stacionárius állapot, egész számú lépés határozza meg, hogy milyen impulzusnyomaték tartozik a landolási pályához.

De hol lép be a kvantummechanikai formalizmusba, hogy az állapotfüggvény által meghatározott impulzusnyomaték csak ћ egész számú többszöröse lehet? Ezt az garantálja, hogy az energia, impulzus és impulzusnyomaték operátoraiban ott szerepel a ћ konstans, mint a differenciálhányadosok együtthatója. Az impulzusnyomaték J_z = iћδ/δφ komponense a tengely körüli forgás poláris szögével képzett differenciálhányados, viszont a szög 360 fokos elfordulás a kezdő állapotnak felel meg. Ennek matematikai következménye, hogy az operátor sajátfüggvénye periodikus lesz, és a teljes fordulat során bekövetkező ismétlődések száma adja meg a diszkrét kvantumszámokat.

1.     5.  A tömeg és az impulzusnyomaték eredete

A tömeggel azonban bajban vagyunk, ugyanis véges tömeg nem mozoghat fénysebességgel, mert a c sebesség miatt végtelenül nagy tömeget észlelne a külső megfigyelő a relativitáselmélet szabályai szerint. Fordítsuk ezért meg a gondolatmenetet, és tegyük fel, hogy épp a c sebességű mozgás felelős a tömeg létrehozásáért! Ez a forgó test legyen az üres tér lokális tartománya, amelynek ugyan nincs tömege, de ez a nulla tömeg matematikai határértékként viselkedik. Az m tömeget, ha megszorozzuk annak reciprokával, akkor egyet kapunk: m·(1/m) = 1. Legyen hát az m tömeg végtelenül kicsi, ha ezt a Lorentz szabálynak megfelelő végtelenül nagy tényezővel szorozzuk, már véges értéket kaphatunk. Ily módon a relativitáselmélet tömegnövekedési szabályát kiterjeszthetjük a tömeg létrehozásának szabályává. A fénysebességű forgás tehát „teremtő” forgás, de az általa létrehozott tömeget már semekkora erő sem tudja úgy felgyorsítani, hogy az elérje a fénysebességet.  Ez a gondolatmenet a fénysebességű forgás koncepciója, amely feloldja az ellentmondást a szóráskísérletekben pontszerűként viselkedő elektron és a véges impulzusnyomaték létezése között. Ez a koncepció új funkciót ad a térnek, amely többé nem passzív tartály, amelyben a részecskék világa elhelyezkedik, hanem a részecskék megalkotója is. A térben minden mozgás sebessége relatív, de van egy nagy kivétel: a fénysebesség, amely a relativitáselmélet szerint mindig azonos vákuumban. Akár hozzánk közelítő, vagy távolodó objektum bocsátja ki a fényt, mindig azonos sebességgel teszi meg felénk az utat. Ezért a fénysebességet mint a tér szerkezeti állandóját foghatjuk fel.

Itt álljunk meg egy pillanatra és gondoljuk végig, hogy mi rejlik három fizikai fogalom: a tömeg, az energia és az impulzus mögött! Hétköznapi tapasztalatainkban az anyagot ösztönösen összekapcsoljuk a tömeg fogalmával, a fizikában azonban az energia és az impulzus játszik főszerepet, különösen a kvantummechanikában. Itt már úgy vetődik fel a kérdést, hogy mi az, ami állandó a változások mögött. Az időbeli állandóságot az energia fejezi ki, de ha a mozgó testre nem hat külső erő, akkor az impulzus jellemzi az állandó sebességű mozgást a térben. Körmozgások esetén, ha nincs külső forgatónyomaték, akkor az impulzusnyomaték képviseli az állandóságot a mozgásban. Ez azt jelenti, hogy az energia, impulzus és impulzusnyomaték a primer fizikai mennyiség, és a tömeg ehhez képest csak másodlagos „segéd paraméter”. Az E = mc² összefüggést úgy kell értelmezni, hogy az energiának van „tömege”, és nem a tömegnek van energiája. Erre a legtisztább példa a foton, amelynek egyaránt van energiája, impulzusa és impulzusnyomatéka, de nem tartozik hozzá nyugalmi tömeg.

 Ha a térben valamilyen ω körfrekvenciával forgás alakul ki, az véges méretű körpályát fog kijelölni, és ennek sugarát az R = c/ω szabály adja meg. Fogjuk úgy fel a fotont, mint a tér forgását, rendeljük hozzá az ω körfrekvenciához az E = ћω energiát. A foton azonban természeténél fogva c sebességgel száguld, vagyis a fénysebességű mozgás által kialakított körpálya egyúttal a forgási tengely irányában is halad szintén fénysebességgel. A foton mozgását úgy is elképzelhetjük, mint a henger palástja mentén feltekeredő csavart. Tisztában kell lenni vele azonban, hogy ez csak szemléltetés, hiszen a fotont alkotó térmozgást nem láthatjuk. Helyesebb ezért a foton és a további elemi részecskék esetén a tér olyan kettős mozgásairól beszélni, amelyet a szimmetriaviszonyok határoznak meg. Körmozgásokban a centrifugális erőn kívül Coriolis erő is fellép, ha ott jelen van egy második mozgás is. Ennek viszont nincs szerepe a fotonoknál, mert ott a haladási irány párhuzamos a forgás tengelyével. A foton másik fontos tulajdonsága, hogy térben nyitott a struktúrája: egy végén nyitott hengerpalást.

Bár a foton nem lehet nyugalomban és így nyugalmi tömege sincs, rendeljük hozzá a tömeg-energia ekvivalencia alapján az m = E/c² fiktív tömeget, ez segíteni fog, hogy kapcsolatot találjunk az energia és az impulzusnyomaték között. Ennek a tömegnek szorzata a fénysebességgel már mérhető mennyiséghez: az m·c impulzushoz vezet, amit ha megszorzunk az R sugárral is, megkapjuk a foton impulzusnyomatékát: ћ = h/2π. A számítás eredménye tehát épp akkora impulzusnyomaték, mint amekkorát Planck annak idején a foton számára megállapított, vagyis a fiktív tömeg fogalmának bevezetése hasznosnak bizonyult! Még arra is választ kapunk, hogy bár a foton frekvenciája és energiája rendkívül széles határok között változik, az impulzusnyomaték mégis pontosan ugyanakkora marad, hiszen amíg a fiktív tömeg a frekvenciával arányos, addig a sugár fordítva arányos vele, a c sebesség pedig állandó.

De térjünk rá a kettős forgással értelmezett elektronra, amely viszont térben zárt struktúra, mégpedig egy gömb. Itt a gömb felülete zsugorodik nullára a fénysebességű forgás miatt, ez tükröződik a Bhabha kísérletben is, amely szerint az elektron hatáskeresztmetszete a szórás kísérletekben nulla. A kettős forgást úgy foghatjuk fel, hogy először egy kiválasztott tengely körül 2π szögű forgatást végzünk el, majd ezt egy erre merőleges tengely körül megismételjük, azaz összességben 4π szögű forgatást hajtunk végre. Ennek a gömbforgásnak frekvenciája az egytengelyű forgáshoz képest fele akkora lesz, azaz Ω = ω/2, a kétszer olyan hosszú szögtartomány miatt. Ezt a gömbfrekvenciát hozzuk kapcsolatba a részecske tömegével: E = mc² = ћΩ, vagyis Planck eredeti gondolatát – aki feltárta ezt az összefüggést fotonokra – kiterjesztjük a részecskékre is. Itt a zárt tértartomány miatt már valódi tömegről beszélhetünk. Ez a felfogás megfelel a kvantumelektrodinamika (QED) szellemének is, ahol az alkalmazott formalizmusban az elektronokat és fotonokat egyaránt oszcillátorok – azaz rezgő objektumok – képviselik. Az impulzusnyomaték egyik komponensét úgy kapjuk meg, ha az egyik tengelyforgás w körfrekvenciáját vesszük alapul, amelyik a fotonhoz viszonyítva kétszeres, azaz ω = 2mc²/ ћ. Ezt behelyettesítve az impulzusnyomaték kifejezésébe, kapjuk, hogy m·c·R = ћ/2. Így jutunk el az S = ½ spinhez, amelyik minden elemi fermion sajátja bármekkora is legyen a tömeg. (Spinnek nevezzük a ћ egységben megadott impulzusnyomaték együtthatóját, ez fotonoknál S = 1, az elektronnál S = ½ értéket vesz fel. Más részecskéket is a spinjükkel jellemezzük, amely bozonoknál S = 1 és fermionoknál S = ½. Az összetett szerkezetű részecskéket is ez alapján osztályozzuk: a spin mindig egész számú bozonoknál, és „félegész” fermionoknál.)

Kvantummechanikában az elektronspin S_z komponenséhez az +½ és -½ sajátértékeket lehet hozzárendelni, és ennek sajátfüggvénye e^±½iφ. Ez a függvény teljes körülforgáskor, azaz φ = 2π értéknél, –1 lesz, és csak a 4π dupla forgásnál lesz +1. Az S = ½ spinekből felépülő rendszerekben a szimmetriákat összegző csoportelmélet ezért a 2π szögű forgást nem tekinti identitásműveletnek, és evvel a szimmetriaművelettel kibővítve bevezeti a kettős csoportokat. Ennek az ad hoc műveletnek a kettős forgás koncepciója adja meg a magyarázatát. A kettős csoport voltaképp a kettős forgásokra épülő matematikai reprezentáció.

1. 6. Centrifugális erő és az erős gravitáció

Ha egy m tömegű test ω körfrekvenciával kering az R sugarú körön, akkor arra F_C = mω²R = mv²/R centrifugális erő hat. Emiatt felvetődik a kérdés, hogy milyen erő képes stabilizálni a forgást a szétrepítő erő kiegyenlítésével? Helyettesítsük be a centrifugális erő képletébe az előzőekben alkalmazott összefüggéseket, ekkor a fénysebességű forgás centrifugális ereje F_C = ћc/R² lesz. Az ellensúlyozó erő megtalálásához forduljunk az általános relativitáselmélethez, amely a tér görbületével magyarázza a gravitációs erőt.

A Newton törvény szerint az M tömegtől r távolságban lévő m tömegre ható gravitációs erő F_G = GmM/r², illetve a hozzá tartozó potenciális energia V_G = GmM/r, ahol G az általános gravitációs állandó. A gravitációs erő tart egyensúlyt az mv²/r centrifugális erővel, amiért

v² = GM/r = V_G/m

Az összefüggés mutatja, hogy a forgás kerületi sebessége nem függ a keringő test tömegétől. Mivel a teret határértékben nulla tömegűnek tekintjük, maga a tér is forog az M tömeg körül, de ennek sebessége messze elmarad c-től. A kerület bizonyos mértékű csökkenése azonban így is bekövetkezik a Lorentz kontrakció miatt, amelyet 2π-vel osztva definiáljuk az r_G < r görbületi sugarat. Ennek segítségével adhatjuk meg a tér görbületét:

. Görbület = 1 – (r_G/r)² = v²/c²

Ez a görbület kis értéket vesz fel a részecskét körülvevő térben, viszont egységnyi lesz fénysebességű forgások esetén. A fenti két összefüggés kapcsolatot teremt a görbület és a gravitációs potenciális energia között:

V_G = Görbület·mc²

A speciális és általános relativitáselmélet összekapcsolásából tehát az adódott ki, hogy a fénysebességű forgás által előidézett egységnyi térgörbület miatt mc² nagyságú potenciális energia jön létre. Eredetileg a görbületet a M tömeg hozta létre, amely vonzza a tőle r távolságban lévő „külső” m tömeget, de amikor a részecske saját tartományába érünk az R sugárnál, ott már nem „külső” tömegről van szó, hanem a fénysebesség által létrehozott saját tömegről, azaz m átveszi M szerepét. Ez a felfogás viszont új értelmet ad a részecskék nyugalmi energiájának, amely nem más, mint a tér torzulásának potenciális energiája fénysebességű forgások esetén. Úgy is fogalmazhatunk, hogy a tér görbülete biztosítja azt az erőt, amely a fénysebességű forgást stabilizálja. Ezt az erőt, amely az R sugarú részecskénél ћc/R² nagyságú lesz, nevezhetjük erős gravitációnak.

A részecskeképződés tehát nem kíván külső energiát, csak az impulzusnyomaték forrását kell biztosítani. Evvel magyarázatot kapunk arra is, hogy a béta-bomlás folyamatában, amikor a neutron protonná alakul át egy elektron és egy neutrínó kibocsátásával, hogyan képződhet olyan közvetítő bozon (W bozon), amelynek tömege közel százszor haladja meg a kibocsátó neutronét.

1. 7. Az elektromos töltés eredete

De honnan származik az elektronok és más részecskék töltése, vagyis hogyan jön létre az elektromágneses kölcsönhatás, és miért van sok nagyságrenddel eltérő tömegű részecskéknek azonos töltése, és miért lehet a töltés előjele kétféle: pozitív és negatív? A QED elmélet részben válaszol a kérdésekre, amikor feltételezi, hogy virtuális fotonok áradnak ki a töltésekből, illetve nyelődnek el. Ezek közvetítik az erőhatást a töltések között, ami lehet vonzás, vagy taszítás, a töltések relatív előjelétől függően. A fotonoknak ugyanis más a polaritása attól függően, hogy a kibocsátó töltés előjele pozitív, vagy negatív, és a fotonok szuperpozíciója dönti el, hogy mikor jön létre taszítás, illetve vonzás a töltött objektumok között. Ha ellentétes a két foton polaritása, akkor a két töltés közötti tartományban az amplitúdók kioltják egymást, ez okozza a vonzást. Ellenkező esetben az amplitúdók összeadódnak ebben a tartományban, és taszítás lesz az eredmény. A QED elmélet azonban nem lép tovább, mert nem válaszol a kérdésre: miért lépnek ki virtuális fotonok a töltésekből? A fénysebességű forgás koncepciója erre a kérdésre is keresi a választ. Ennek magyarázatát egyrészt a tér szerkezetére, másrészt tehetetlenségi erőkre lehet visszavezetni.

A háromdimenziós teret kétféle módon építhetjük fel. Ha megadunk két merőleges koordinátát, nevezzük x-nek és y-nak, akkor a harmadik tengely két irányban is felvehető: z mutathat felfelé, vagy lefelé. A két geometria nem forgatható egymásba, ahogy a jobb és bal kezünk se, viszont ezek egymás tükörképei. Ezt a kettősséget nevezzük kiralitásnak. Ez a kettősség jelenik meg a kettős forgás esetén is. Válasszuk ki az első forgást az óramutató járásával egyezően, a másik erre merőleges forgás iránya viszont lehet akár egyező, akár ellentétes az óramutató járásával, azaz a kettős forgás is lehet kétféle kiralitású. Ennek megfelelően létezhet kétféle részecske, kétféle anyag. Ez áll az anyag és antianyag kettőssége mögött. Mi történik, amikor az anyag találkozik az antianyaggal, például az elektron a pozitronnal? Ilyenkor a két részecske megsemmisül, és két gamma foton távozik. Ezt képszerűen értelmezi a kettős forgás modellje: két ellentétes irányú forgás megsemmisíti egymást, de a második forgás megmarad, ez pedig nem más, mint a két gamma foton!

Ez arra is rámutat, hogy miért sikertelenek azok a matematikai próbálkozások, amikor a részecskefizikában – ilyenek a húrelméletek is – négy, öt vagy még további térdimenziókkal próbálkoznak. Ha például létezne egy negyedik térdimenzió, akkor a térnek nem két, hanem négyféle kiralitása lenne, tehát nemcsak anyag és antianyag létezne, hanem volna még két további anyagtípus is. Ennek hiánya viszont arra mutat, hogy meg kell elégednünk a jól bevált háromdimenziós világképpel. De mi a helyzet Minkowski négydimenziós téridő koncepciójával? Van egy alapvető különbség a tér és az idő dimenziók között. Amíg a térdimenziók kétirányúak: föl-le, jobbra-balra, előre-hátra, az időben nem lehet visszafelé menni a múltba. Emiatt a téridő nem jár további anyagtípusok megjelenésével.

De milyen erő készteti a fotonokat, hogy kilépjenek a töltött részecskékből? Ha forgó rendszereken belül van egy további mozgás, arra hat egy újabb tehetetlenségi erő, amit Coriolis erőnek nevezünk. Ennek iránya egyaránt merőleges a másodlagos mozgás irányára és a forgás tengelyére, amit vektorszorzat fejez ki:

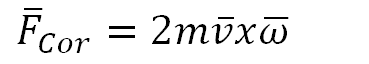
A második forgás iránya az első forgás tengelyéhez képest körbefut, ami szinuszos függést eredményez, melynek amplitúdója c sebesség mellett ħc/R²:

1. Ábra. A Coriolis erő szemléltetése kettős forgások esetén. Az x-tengely körül megy végbe az elsődleges, az y- körül a másodlagos forgás, amire ható erő két maximumát a fekete nyilak mutatják, a jobboldalon pedig a szinuszos változás látható

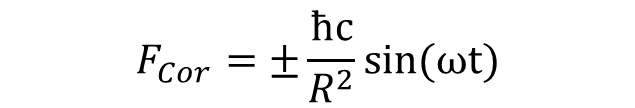
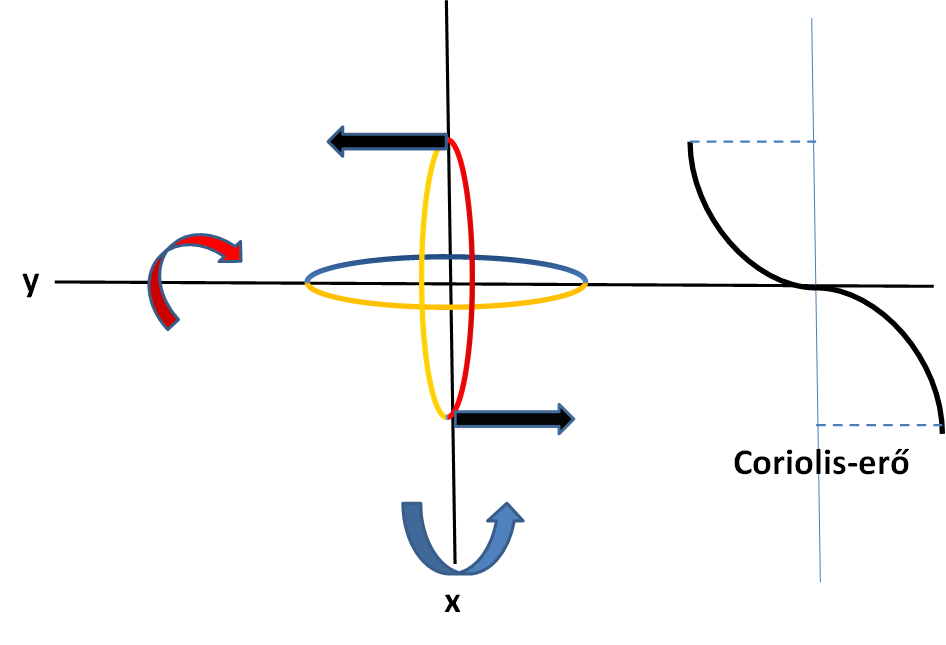
Ez az erő párhuzamos a második forgás tengelyével, és előjelét a kettős forgás kiralitása határozza meg. A Coriolis erő átlaga nulla, amely viszont ω frekvenciával változó erőt generál a kettős forgás gömbjének felszínén, amelynek nagysága a centrifugális erővel együtt nulla és 2ħc/R² között ingadozik. A részecske sajátforgását stabilizáló erős gravitáció görbületi sugara is ennek ütemében pulzál, amely forrásává válik a külső térbe távozó egytengelyű forgásoknak, amit a QED virtuális fotonoknak nevez.  A kiralitásnak megfelelő előjel a forgás polaritását határozza meg. A kilépési hatásfokot az α = 1/137 Sommerfeld állandó adja meg, amely meghatározza a Coulomb kölcsönhatásban definiált elemi töltés nagyságát: e² =αħc. A töltés tehát nem függ a részecske méretétől! Evvel választ kapunk arra a kérdésre is, hogy a rendkívül eltérő tömegű részecskéknek miért ugyanakkora az elektromos töltése.

De térjünk még vissza az einsteini gravitáció létrejöttének okára is. Ezt az M tömeg körüli térforgásokra és az általa kiváltott térgörbületre vezettük vissza. Két kérdés azonban tisztázatlan maradt. Eddig csak a frekvenciáról beszéltünk, de egyrészt milyen irányban történik a forgás, másrészt miért fog forogni a tér?

Az első kérdés megválaszolásához a kvantummechanika szemléletmódját vehetjük alapul. Amikor atomok és molekulák elektronjainak pályájáról beszélünk, csak valószínűségi kijelentéseket tehetünk az állapotfüggvény segítségével. Ennek oka, hogy nem tudjuk az elektron pályáját stacionárius állapotban nyomon követni, csak az ugrásokat láthatunk két pálya között. Természetesen a tér forgásait sem láthatjuk, ezért konkrét forgási pálya helyett csak annyit mondhatunk, hogy a centrumtól mért valamilyen r távolságban minden pályairányhoz azonos valószínűség tartozik. Amikor egy égitest pályáját nyomon követjük, az már egyet kiválaszt a lehetséges pályák közül. Ennek felel meg a kvantummechanikában, amikor az állapotfüggvény által megengedett lehetőségek közül a mérés egy konkrét értéket ad meg. A kvantummechanikából ezért nem a kvantumot kell átvenni, hanem az elmélet valószínűségi felfogását.

A másik kérdés megválaszolásához segítséget ad az a kép, amivel az elektromágneses kölcsönhatást közvetítő virtuális fotonok kilépését magyaráztuk. De mielőtt ezt bemutatnánk, tegyünk egy újabb kitérőt az elektron anomális mágneses nyomatékának kérdésköréhez.

1.     8. Az elektron anomális mágneses nyomatéka

Az elektronok véges mágneses nyomatékkal rendelkeznek, melyet a relativisztikus Dirac-egyenletből lehet származtatni:

    M_S = 2μ_BS,

ahol μ_B = eћ/2mc a Bohr magneton. Ezt származtatni tudjuk az e elemi töltés fénysebességű forgásából is! Itt hangsúlyozni kell, hogy ebben a mozgásban az elektron saját mágneses nyomatéka végez körforgást külső mágneses mezőben (Larmor precesszió), azaz a fénysebességű kettős forgásra rárakódik egy ahhoz képest lassú egytengelyű forgás is. Alkalmazzuk a mágneses nyomaték számításánál a klasszikus elektrodinamika M = IF/c törvényét! Itt az f frekvenciával forgó e töltés árama I = e·f = eω/2π, a bezárt kör területe F = R²π.  A behelyettesítések után kapjuk, hogy:

M_S = eR/2 = μ_B = 2μ_BS

Az atomban „keringő” elektronok pályamozgásához is tartozik mágneses nyomaték, mégpedig ha a pálya impulzusnyomatéka Lħ, ennek nagysága M_L = μ_BL. Összehasonlítva a két nyomatékot, feltűnik, hogy a spin szorzójaként szerepel egy 2-es együttható, de mi ennek az eredete? Ennek megválaszolásával a fizika már régóta küszködik, és látszólag a klasszikus fizika nem tudja megadni a választ. A kettős forgás koncepciója azonban kézenfekvő magyarázatot ad! A spint kettős forgásból származtatjuk, ezért lesz S = ½, viszont a mágneses nyomaték a mágneses mező körüli Larmor precesszióból – azaz egytengelyű forgásból – ered. Az egytengelyű forgásból származtatott mágneses nyomatékot a kéttengelyű forgásból kapott impulzusnyomatékkal összevetve lép fel a formulában a 2-es faktor.

A mágneses nyomaték rendkívül pontos kísérleti értéke azonban nem pontosan egyenlő a relativisztikus Dirac-egyenletből származtatott faktorral, hanem kissé nagyobb:

 M_S = 2,002319304362 μ_BS

Mi okozza ezt a kis növekményt? A kvantum-elektrodinamika (QED) mezőelmélete erre rendkívül pontos megoldást ad különböző szintű közelítések keretében. A QED alapgondolata, hogy az elektromos töltések vonzó-taszító hatását virtuális (közvetlenül nem detektálható) fotonok hozzák létre, amelyek állandóan kibocsátódnak és elnyelődnek, és így fluktuációt okoznak a részecske pozíciójában. Ez viszont megnöveli a mágneses nyomatékot az áram által körüljárt terület kiterjesztése által. A nehéz veretű időtől-függő perturbációs eljárás számba veszi a fotonok és elektronok legkülönbözőbb mozgásait, emissziós, abszorpciós, párképződési és annihilációs folyamatait, és ezáltal tíz jegy pontossággal tudja reprodukálni a kísérletileg mért értéket. Itt most bemutatjuk, hogy a legfontosabb korrekciós tagok a klasszikus elektrodinamika eszközeivel is származtathatók, ha a fénysebességű forgások elvére támaszkodunk.

A részecske belső tartományából való foton kibocsátást a kettős forgás által kiváltott és ћc/R² amplitúdójú Coriolis-erő oszcillációja okozza, és a fotonok kilépési hatásfokát az α = 1/137,036 Sommerfeld állandó adja meg. Az elektron saját mozgását stabilizáló erős kölcsönhatásnak a ћc/R² nagyságú centrifugális erő és a kiáramló αћc/R² nagyságú Coulomb erő összegét kell ellensúlyozni, ami lecsökkenti az erős gravitáció R_G sugarát a centrifugális erő R_C sugarához képest. Viszont ezt a hatást csak a mágneses mezőre merőleges síkban kell figyelembe venni a gömb egész felületén ható centrifugális erővel szemben, ezért a korrekciós tagban fellép a sugár/kerület 1/2π tényezője is: 

ћc/R_G² = ћc/R_C² + (α/2π)ћc/R_C²

Innen kapjuk a töltés által körüljárt felület megnövekedését:

R_C²/R_G² = 1+ α/2π

Ez az arány jelenik meg az elektron anomális mágneses nyomatékának első korrekciós tagjában. (Bár a mágneses nyomaték lineárisan függ a részecske sugarától, mégis a felülettel való arányosság határozza meg a korrekciót, mert a tömeget létrehozó ω = c/R körfrekvencia azonos marad.) A számítás tovább finomítható, ha figyelembe vesszük, hogy a kiáramló fotonok energiája csökkenti az elektron belső terének energiáját 1 - α/2π mértékében:

R_C²/R_G² = 1+ α/2π(1 - α/2π)

Ekkor a mágneses nyomaték már csak a hetedik tizedes jegyben tér el a kísérleti adattól: M_S = 2,00232010 μ_BS.

A QED számítások még három további tizedes jegyig rekonstruálják a kísérleti értéket, de ekkor már rendkívül összetett virtuális folyamatok sokasága is szerepet játszik, amit a Feynman diagramok foglalnak össze (R. P. Feynman: QED. The strange theory of light and matter, Princeton University Press, 1986). A klasszikus fizika eszközével számított érték is tovább közelíthető a kísérleti adathoz, ha figyelembe vesszük az elektron-pozitron párkeltést is. Ilyenkor nem a tömeg „megtermeléséről” van szó, hanem megfordul az elektromágneses energia áramlási iránya: eredetileg az elektronokból léptek ki a fotonok, ekkor viszont a fotonok építik fel az elektront és a pozitront. A belső energiának α/2π hányadát képviseli a virtuális foton mező a Larmor precesszió síkjában, a párkeltéshez egyfelől két foton kell, másfelől két részecske keletkezik, és ennek megvalósításához a kilépő energia α/8π hányadát kell „befektetni”. Ezt számításba véve a tovább finomított összefüggés:

R_C²/R_G² = 1+ α/2π(1 - 5α/8π)

Az innen számított mágneses nyomaték M_S = 2,00231944 μ_BS még közelebb került a kísérleti adathoz. További korrekciós tagok bevezetése nélkül is figyelemre méltó, hogy a fénysebességű forgások koncepciójára támaszkodva a klasszikus fizika egyszerű eszközei is meglepően jó egyezést adnak a kísérlettel, amihez ugyanakkor a QED rendkívül bonyolult és számítógép igényes integrálásokkal jut el.

A mágneses nyomaték anomáliájának okát szemléletesen avval magyarázhatjuk, hogy az elektronnak kettős héja van. A belső felület határozza meg a tömeget és az impulzusnyomatékot, a külső felület viszont a fluktuációs mozgás miatt alakul ki, amiben a belső gömb „lötyög”, és emiatt megnövekszik a felület, amit a töltés körbejár.  

1.     9. A fénysebességű kettős forgás gravitációs mezője

Folytassuk annak a kérdésnek a vizsgálatát, hogy miért forog a tér az M tömegű fizikai objektumok körül? Erre a rövid válasz, hogy ennek oka, a részecskét alkotó kettős forgás „kiáradása” és elnyelődése a külső térből! Ez annyiban hasonlít a virtuális fotonok szerepéhez, hogy a gravitációs mezőt is folytonos emisszió és abszorpció építi fel. Mivel a távolság négyzetével növekszik az elért felület, így a mezőerősség r² arányában csökken. A két erőtörvény ebben hasonlít egymásra. Másik hasonlóság a két kölcsönhatás között, hogy a mezőt létrehozó és a hatást átvevő objektumok – itt a töltés, ott pedig a tömeg – szimmetrikus, egyenrangú, szerepet töltenek be: gravitációnál két tömeg, a Coulomb kölcsönhatásban két töltés szorzata szerepel. A szorzat két tényezőjének azonos szerepe annak felel meg, hogy az emisszió és abszorpció két egyenértékű tükörfolyamat. Mégis van egy alapvető különbség a két kölcsönhatás között: amíg a foton fénysebességű forgás, amihez kvantált impulzusnyomaték tartozik, addig a lassú kettős forgások nem hoznak létre impulzusnyomatékot és így nincs kvantumuk sem. A különbség abban nyilvánul meg, hogy az elektromágneses kölcsönhatás nemcsak pályafenntartó mező, hanem pályaváltozásokat (ugrásokat) is indukál, ez előbbi közvetítőit nevezi a QED virtuális, az utóbbit valódi – megfigyelhető – fotonoknak. Az energia nyelvén megfogalmazva ez azt jelenti, hogy a fotonok egyrészt megalkotják a kölcsönhatás potenciális energiáját, másrészt van kinetikus energiájuk és ehhez kapcsolódóan impulzusuk is. A lassú gravitációs kettős forgások viszont kizárólag potenciális energiát hoznak létre a térgörbületek által, anélkül, hogy rendelkeznének kinetikus energiával, illetve olyan lökő erővel, amely a pályák között ugrásokat hozhatna létre. Ennek a döntő különbségnek figyelmen kívül hagyása okozhatja, hogy immár száz éve kudarcba fulladnak az erőfeszítések, hogy megtalálják a gravitáció kvantumát, és megalkossák a fizika négy kölcsönhatásának egységes mezőelméletét.

Az utolsó megválaszolandó kérdés, hogy milyen erő indítja útjára a kettős forgásokat a részecske határán kívülre? Ez az Euler erő, ami akkor lép fel, ha a forgási frekvencia megváltozik! Ez a forgás felgyorsításával, vagy lassításával szembeni tehetetlenség, amelynek nagyságát vektoriális szorzat fejezi ki:

A fénysebességű forgás koncepciója szerint a részecske ω frekvenciája gyakorlatilag nullára csökken, amikor átlépjük a részecske R sugarát, és mivel ott a gravitációs forgás frekvenciája nagyon kicsi, a frekvenciaváltozás egyenlő a forgási frekvenciával, azaz Δω = ω. A Δt idődifferencia megadásához az R sugarú elektron αR vastagságú héjának αR/c áthaladási idejét vehetjük alapul, amiért a forgómozgás irányában ható Euler erő:

Ez hatalmas erő, amely még a részecskét stabilizáló erős kölcsönhatást is 137-szer meghaladja, viszont ennek munkavégző képessége az αR szakaszra korlátozódik, azaz V_Euler = ħc/R = Mc². Bár a részecske forgási frekvenciája az R határon átlépve közel nullára csökken, mégis valamennyi megmarad, ezt úgy is felfoghatjuk, mint a nem kvantált folyamatok folytonossági követelményét. A kilépő forgási frekvencia miatt van tömegvonzás! A forgás kiléptetését okozó erőt származtathatjuk az Euler potenciálból. Ennek a potenciálnak viszont két független forgást kell kivinnie a részecske külső terébe, és emiatt a létrehozott V_G/m gravitációs potenciál az Euler potenciál négyzetével lesz arányos:

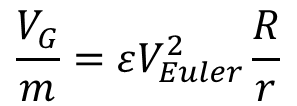
Az ε arányossági konstanst meghatározhatjuk, ha összevetjük a két potenciált a részecske r = R határánál, amiből kapjuk, hogy 

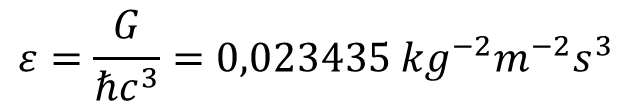
Az ε konstans a fizikában korábban még nem alkalmazott állandó, amely hasonló szerepet tölt be a gravitáció elméletében, mint az a Sommerfeld állandó az elektromágnességben. Ez az állandó úgy fogható fel, mint csillapítási tényező, amely meghatározza az Euler erő képességét gravitációs forgások létrehozására. Mivel a gravitációt két összekapcsolt forgás hozza létre, a vonzóerő nagyságát a tömeg határozza meg, szemben a töltések által meghatározott Coulomb erővel, amelyet egytengelyű forgások, azaz fotonok közvetítenek. A kettősforgás kiralitása viszont nem játszik szerepet a görbületi sugár előjelében, amely magyarázza, hogy a gravitáció kizárólag vonzást, és nem taszítást hoz létre a részecskék között. Arra már korábban utaltunk, hogy az elektromágnesesség vonzási-taszítási kettőssége a fotonok két lehetséges forgási irányával van összefüggésben.

Einstein általános gravitációs egyenletéből Schwartzshield határozta meg a módosított gravitációs potenciált körmozgások esetén, amely kiegészíti az eredeti Newton formulát:

V_G/m = GM/r + G²M²/c²r² 

Ez a kiáramló kettős forgások koncepciójával is magyarázható. Az M és m tömegek közötti GMm/r gravitációs potenciális energia fele-fele arányban hozzájárul a részecskék lokális Mc² illetve mc² energiájához, ami viszont megegyezik a helyi Euler potenciális energiával. Emiatt megnövekszik a kettős forgás kibocsátási hatásfoka is:

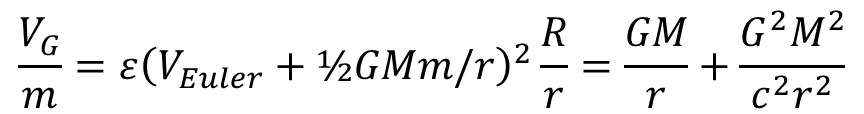
Itt a négyzetre emelésnél az utolsó kis tagot elhagyva reprodukáltuk a Schwartzshield potenciált. Ebből látható, hogy a kettős forgásokra alapozott gravitációs modell összhangban van az általános relativitáselmélet formalizmusával is.

1.     10.   Miért lesz végtelen az elektron sajátenergiája a QED elméletben?

A QED elmélete látványosan szép eredményre vezet az elektron anomális mágneses nyomatékának meghatározásával, mégis van egy súlyos hibája: a sajátenergia első perturbációjának számítása végtelenül nagy értékre vezet. Ha ezt önkényesen elhagyjuk, akkor a további tagok rendkívül nagy pontossággal adják vissza a kísérleti értéket. Az elméletnek ezt a gyenge pontját a klasszikus elektrodinamikától örökölte, amikor számba vette az elektron elektromos kölcsönhatásának sajátenergiáját. Ezt úgy végzik el, hogy az elemi töltést végtelenül kis elemekre bontják fel, és először elviszik ezeket a töltéseket végtelen távolságba, majd kiszámítják a munkavégzést, amikor a töltést egyetlen pontba egyesítik. Az alkalmazott módszer eleve ellentmondáson alapul, amikor felbontja az oszthatatlan elemi töltést. A végtelen sajátenergia pedig onnan származik, hogy az integrálást nulláig viszik, mintha tényleg egyetlen matematikai pontban lenne a töltés, ahol már a taszítási erő ellen végzett munka végtelenül nagy. A QED elmélete is a kölcsönhatást nulláig kiterjesztett integrálokkal írja fel, ezért jelenik meg ott is a szingularitás. Ezt a hibát kiküszöböli a fénysebességű forgás koncepciója, amely véges sugarat határoz meg a részecske számára. Az elektromágneses mező energiája a részecske által a belső tartományból a külső térbe kiküldött hányad, amit az a Sommerfeld-állandó ad meg, míg az mc² sajátenergia döntő hányada (1 – α = 0,9927-ed  része) belül marad. Helytelen ezért az olyan próbálkozás is, amely az elektromágneses mező energiájával akarja értelmezni az mc² nyugalmi energiát (erre alapozzák a klasszikus elektronsugarat).

1.     11.  Összetett részecskék spinje és a véges hatáskeresztmetszet

A pontszerűséggel kapcsolatban érdemes még kitérni arra a kérdésre is, hogy a proton töltéseloszlása a mérések szerint nem pontszerű, bár az elektronhoz hasonlóan a spinje ½. Az elektron impulzusnyomatékát a fénysebességű kettős forgásra vezettük vissza, ezért ha evvel magyaráznánk a proton spinjét is, akkor nulla hatáskeresztmetszetet várnánk proton esetén a szóráskísérletekben. Ha nem tudnánk az elméletből, hogy a proton három kvarkból épül fel, akkor már a véges hatáskeresztmetszet létezéséből levonhatnánk a tanulságot, hogy a proton összetett szerkezetű! Mivel a valóban elemi – tehát tovább nem osztható – fermionoknak a kettős forgás koncepciója szerint ½ a spinje, így a spinek összeadási szabályából már következik, hogy legalább három komponensből épül fel a proton, ugyanis két ½ spin összege nulla, vagy egy lehet. Egyébként az összetett részecskék családjában vannak két kvarkra bontható mezonok is, ahol tényleg a spin 0, vagy 1 értéket vesz fel. Három ½ spin alkothat akár ½, akár 3/2 spint is. Léteznek ennek megfelelően olyan barionok is, melyeknek spinje 3/2. (Barionnak nevezzük a három kvarkból, vagy antikvarkból felépülő részecskéket, ennek legstabilabb két tagja a proton és a neutron).

Következő rész:

 A blog további írásai: "Paradigmaváltás a fizikában"

Két kölcsönhatás eltérő világa

Aligha lehetne két jobban eltérő kölcsönhatást találni, mint az elektromágneses és a gyenge-kölcsönhatás. Az elektromágnesesség közvetítője a foton akár milliárd fényév távolságból is megérkezhet hozzánk egy távoli galaxisból, szemben a gyenge-kölcsönhatást közvetítő W és Z bozonokkal, melyek hatótávolsága az atommagnál is kisebb, úgy 10^–16 m nagyságába esik. Elmondható ez az élettartalmukról is, a távoli galaxisokból érkező foton milliárd éves utazás után is megfigyelhető, míg a W bozon élettartama nem hosszabb 10^–24 másodpercnél. Szintén nagyon eltérnek tömegükben és töltésükben is, a fotonnak nincs nyugalmi tömege, míg a két gyenge-kölcsönhatási bozon a részecskevilág nehézsúlyú bajnoka, ha eltekintünk a Higgs bozonnak tulajdonított részecske tömegétől, akkor valamennyi egyéb megfigyelhető részecske tömegét meghaladja a W és Z bozoné. Ami pedig a töltésüket illeti, a fotonnak nincs, a W bozon pedig +e illetve –e elemi töltéssel rendelkezik, hasonlóan az elektronhoz és a pozitronhoz. A W⁺ és W^– egymás részecske-antirészecske párja, míg a fotonok világa nem ismeri ezt a kettősséget. Abban is nagy a különbség, hogy az elektromágnesesség kölcsönhatási erőt (vonzást vagy taszítást) hoz létre két objektum között, míg a gyenge-kölcsönhatás átalakítja az egyik részecskét a másikba.  Abban is különböznek, hogy az elektromágneses kölcsönhatás csak töltött objektumok között jön létre, viszont a gyenge-kölcsönhatás minden részecskére hat. Csupán egy dologban egyeznek: spinjük egyaránt S = 1, azaz bozonokról van szó. Evvel szemben sokkal nagyobb a hasonlóság az elektromágnesesség és a gravitáció között, nézzük akár az időtávot, vagy a kölcsönhatások távolságfüggését. Ezért hatott a fizikus társadalomban meglepetés erejével, hogy a gyönge- és elektromágneses kölcsönhatás közös elméleti alapra helyezhető, míg a gravitáció nem volt bevonható az egyesített mezőelméletbe (Sheldon Glashow. Steven Weinberg, Abdus Salam, Nobel díj: 1979).    

Az átalakulások megmaradási elve

A gyenge- és elektromágneses kölcsönhatás eltérésének és ugyanakkor mélyen fekvő hasonlóságának megértéséhez szemléletes kulcsot ad a részecskék fénysebességű forgásmodellje. Először azt kell megértenünk, hogy milyen állapotváltozást hoz létre a két kölcsönhatás. Az elektromágnesesség hatását legkönnyebb az elektron példájával szemléltetni. Az atomban, vagy molekulában kötött elektron pályáját az impulzusnyomatékkal jellemezhetjük, melynek értéke a redukált Planck-állandó többszöröse: Lℏ. Az elektron állapotváltozása során az L kvantumszám eggyel változik, legyen szó foton elnyelésről (abszorpció), vagy kibocsátásról (emisszió). Ilyenkor az elektron pályamozgásának változása hozza létre a foton S = 1 spinjét, azaz ℏ impulzusnyomatékát.  Szemléletesen úgy mondhatjuk, hogy az elektron „keringő” mozgása konvertálódik a foton saját forgásává. Hasonló magyarázat adható, amikor értelmezzük mágneses mezőben Larmor-precessziót végző S = ½ spinű elektronok rezonancia átmeneteit, ekkor a spin mező irányú komponense egységnyit változik a foton abszorpciója, vagy emissziója során. Ebben az esetben a mágneses mezőben polarizált elektronspin megváltozása biztosít forrást a foton impulzusnyomatékához. Mindkét esetben az energia-megmaradás mellett az impulzusnyomaték megmaradása vezet a kvantumátmenetek kiválasztási szabályához. Ehhez még hozzá kell tenni, hogy az átmenetek során az elektronok nyugalmi tömege nem változik meg.

Annihiláció és párképződés

Létezik egy másik kapcsolat is a fotonok és a részecskék között, az annihiláció és a párképződés. Az előbbi esetben egy-egy azonos tömegű részecske és antirészecske eltűnik gamma-sugárzás létrejöttével, a másik folyamat ennek fordítottja, amikor a foton létrehoz egy részecske-antirészecske párt, például egy elektront és egy pozitront. Ez már a nyugalmi tömeg létrejöttének és eltűnésének folyamata. A kiválasztási szabály, hogy az energia, a töltés és a spin (impulzusnyomaték) megmaradjon.  Mivel a fotonnak nincs töltése, ez a szabály azt jelenti, hogy a képződő két részecske ellentétes előjelű töltéssel rendelkezik, másrészt a foton S = 1 spinje megköveteli, hogy a két új részecske egyaránt ½ spinnel rendelkezzen. A fénysebességű forgásmodellben a feltétel azáltal teljesül, hogy az elektron és pozitron kettős-forgásának ellentétes a kiralitása, és így az annihiláció során kioltódik a „második” forgás az ellentétes sodrásirány miatt, miközben az „első” forgás megmarad, ami pedig nem más, mint a foton. A „második” forgás megszűnéséhez az is kell, hogy a frekvenciák megegyezzenek, azaz csak két azonos nyugalmi tömegű részecske és antirészecske semmisítheti meg egymást. Párképződéskor viszont megfordul a helyzet, ekkor a fénysebességű haladó mozgás két ellentétes perdületű forgásra hasad fel, amiért a képződő kettős-forgások kiralitása, azaz töltése ellenkező előjelű lesz, a foton ℏ impulzusnyomatéka pedig két egyenlő részre válik szét.

Leptonok

Térjünk át a részecskeátalakulások megmaradási szabályaira! Nézzük meg ehhez az elektron (e) és „nagy testvérei” a müon (μ) és a tau részecske (τ) esetét! Ezek a töltött leptonok, amit „anyagnak” nevezünk, ha a töltés negatív, és „antianyagnak”, ha pozitív. Szintén a leptonok közé tartoznak a töltéssel nem rendelkező neutrínók (ν). Ebben a „családban” a töltés és a spin azonos, viszont a nyugalmi tömeg erősen különbözik, a müon tömege 207-szer, a tau részecskéje 3477-szer nagyobb az elektronhoz viszonyítva. (A három részecske energiája: 0,511 illetve 105,66 és 1776,8 MeV.) Honnan származnak ezek az arányok? Erre a részecskék tulajdonságait összegző Standard Modell sem adja meg a választ, ezért ezeket az értékeket fogadjuk el, mint kísérleti tapasztalatot. A két nehezebb részecske a stabilis elektronnal szemben viszonylag rövid életű (müon: 2,2x10^–6 s, tau: 2,9x10^–13 s) és bomlásuk egyik végterméke az elektron. A részecskék világában ez az élettartam nem számít rövidnek, mert amikor gamma-sugárzás jön létre a részecskék bomlás során  10^–20 s a tipikus felezési idő. A viszonylag lassú bomlás oka, hogy leptonoknál a gyenge-kölcsönhatás idézi elő a folyamatot, ahol az elektromágneses átmenetek tiltottak.

A gyönge-kölcsönhatási bozon spirálmozgása

Az első kérdés, ami felmerül, hogy miért nem gamma-sugárzás kibocsátásával megy végbe a bomlás, hiszen sem a spin megmaradás, sem a töltésmegmaradás szabálya nem sérülne (a töltés nem változik, a spin vetületi kvantumszám ½ és –½ közötti ugrása pedig kiegyenlítődik a foton S = 1 spinje révén). Az ilyen átmenet tiltását a részecskék fénysebességű forgásmodelljével értelmezhetjük. A foton egytengelyű forgás, amely a kéttengelyű forgás (tehát a fermion) egyik komponensét tudja megváltoztatni. Ahhoz, hogy mindkét forgási frekvencia megváltozzon két lépésre van szükség. Első lépésben a gyenge-kölcsönhatás szétválasztja a töltést és a tömeget két független részecske létrehozásával. Az egyik a fotonhoz hasonlóan bozon (S = 1), a másik fermion (S = ½), ez megfelel az impulzusnyomaték megmaradási szabályának. Az így képződő W bozon azonban jelentősen különbözik a fotontól, mert átveszi a müon töltését és van jelentős tömege is. Egytengelyű forgásnak úgy lehet töltése, ha a fénysebességű terjedési irány merőleges a forgástengelyre, mert ekkor fellép a Coriolis-erő, ami a töltés létrehozója. Ez a mozgás spirálist hoz létre a forgási sugár növekedése miatt, amit az r = r₀ + ct összefüggés ír le. Itt r₀ = h/m₀c a W bozon Compton-sugara. Az ω körfrekvenciájú forgás kerületi sebessége c = ωr, ezért a sugárnövekedés a körfrekvencia csökkenésével jár az

egyenlet szerint, ahol az ω₀ frekvencia a W bozon m₀ tömegéből számolható a ℏω₀ = m₀c² ekvivalencia elv alapján. A frekvenciacsökkenés a tömeg, illetve a részecske energiájának csökkenését hozza magával. A W bozon kísérletileg meghatározott tömegét ezért lokális képződési tömegnek kell értelmezni és nem nyugalmi tömegnek, hiszen a fénysebességű terjedés miatt a kölcsönhatási bozon nem lehet nyugalomban. A fotontól eltérően mégis jogunk van tömegről beszélni, mert a W bozon energiája és az ennek megfelelő E/c² tömege a tér egy szűk tartományára lokalizálódik. A W bozon fokozatosan csökkenő körfrekvenciája teszi számára lehetővé, hogy a részecske átalakítás „csavarkulcsa” legyen, mert kapcsolatot teremthet a különböző tömegű – azaz forgási frekvenciájú – részecskék között.

Az átalakulások mellékterméke: a neutrínó

 Nem ejtettünk még szót az átalakulás másik részecskéjéről, a neutrínóról, amit a folyamat „hulladék anyagának” tekinthetünk. Ennek nincs sem nyugalmi tömege, sem töltése. A Fermion-egyenlet általánosításával lehet értelmezni az elektron és neutrínó tulajdonságait (Lásd: Rockenbauer Antal: A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója, Scolar Kiadó, 2017, pp. 202-205). Az előbbinek van saját tömege és töltése, de nincs saját impulzusa, míg az utóbbi rendelkezik saját impulzussal, de nincs sem tömege, sem töltése. Épp a saját impulzus teszi lehetővé, hogy létezhetnek különböző tulajdonságú neutrínók, amit elektron, müon illetve tau típusú neutrínónak nevez a szakirodalom, és ezek egymásba alakulási folyamata a neutrínó oszcilláció.

Honnan származik a W bozon óriási tömege?

A gyenge-kölcsönhatás első lépésének van egy különös tulajdonsága: a képződő W bozon tömege, sokkal nagyobb, mint a forrásul szolgáló részecske, jelen esetben a müon saját tömege, de ez igaz a többi átalakulási folyamatban is, így például a neutron béta-bomlásában. Ezt is magyarázza a fénysebességű forgásmodell, mely szerint a tér a forgási frekvencia mértékében torzul negatív potenciális energiát létrehozva, amely ellensúlyozza a forgás pozitív kinetikus energiáját, azaz a potenciális energia és a mozgási energia összege mindig nulla marad. A forgás lassulását úgy kell értelmezni, hogy a csatolás erőssége a részecske és a tér között fokozatosan csökken.

Impulzus szerepe az átalakulásban

Az átalakulási folyamatban szó kell, hogy essék az impulzusról is! A kilépő neutrínó impulzussal rendelkezik, ezt a megmaradási elv szerint a W bozon saját impulzusa egyenlíti ki. Mivel fénysebességű terjedésről beszélünk, ez a saját impulzus a pc = E összefüggésből határozható meg, hasonlóan a fotonhoz. Az impulzus viszont irányfüggő mennyiség, ezért a W bozon terjedésének kitüntetett iránya van. Ez a polarizációs irány játszik fontos szerepet az átalakítási folyamat második lépésében. Ez a lépés az első megfordítása, ebben a W^– bozon átalakul elektronná egy második neutrínó kibocsátása mellett, de ez már jóval kisebb energiával történik, mert a spirálmozgás során a körfrekvencia lecsökkent. De mekkora ez a csökkenés? Nézzük meg a forgás fázisának változását, amit a frekvenciaváltozása miatt integrálással határozhatunk meg:

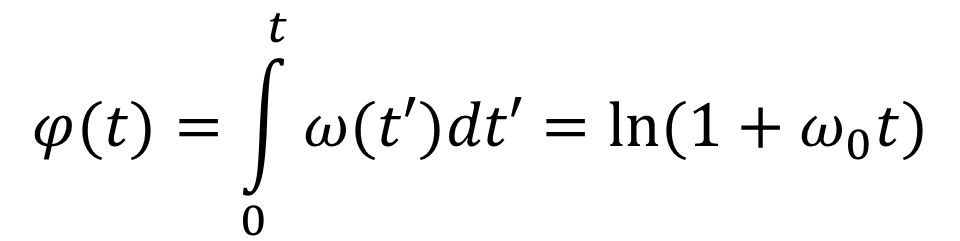
A fázis változását a sugár függvényében logaritmikus skálán mutatja az ábra.

A W bozon spirális pályája logaritmikus ábrázolásban, a fekete nyíl a tau, a zöld a müon, a piros az elektronkilépés pozícióját mutatja

A W bozon aktív fázisai

A következő kérdés, hogy a spirálmozgás milyen fázisánál következik be a második lépés, amikor képződik a két lepton? A spirálmozgás során fokozatosan csökken a W bozon energiája, ami végbemehet, mert a tér görbülete – és így a kiegyenlítő negatív potenciális energia – evvel együtt csökken. A W bozon azonban nyomtalanul nem tűnhet el, mert ekkor sérülne az impulzusnyomaték és a töltés megmaradási törvénye. Létezik azonban három „kijárat”, amikor képződik a két lepton, felhasználva a töltést és az impulzusnyomatékot is. Ezt a kijáratot a W bozon kezdő iránya szabja meg: akkor jön létre átalakulás, amikor egy-egy félfordulat végbemegy, ugyanis ekkor az impulzus újra az eredeti iránnyal lesz párhuzamos. Ennek megfelelően bármelyik π szögű elfordulásnál létrejöhet a két lepton. Vezessük be a ρ = 1 + ω₀t tömegcsökkenési arányt, ami π szögű elfordulásnál e^π = 23,14 nagyságú lesz. Ez azt jelenti, hogy amikor az eredeti tömeg ilyen mértékben csökken, bekövetkezhet a W bozon átalakulása. Ezt is szemlélteti a fenti ábra. A W bozon induló energiája E₀ = 80,395 GeV a mérések szerint, ez lecsökken az első félfordulat után E_π = 3,4738 GeV, a másodiknál E_2π = 150,1 MeV, a harmadiknál E_3π = 6,487 MeV értékre. Ezen az energián osztozik a létrejövő két fermion. Rendeljük a tau, müon és elektron, valamint a megfelelő neutrínókhoz az n = 1, 2, 3 kvantumszámot, az előbbieknél az m_n nyugalmi tömegből, az utóbbiaknál a p_n saját impulzusból számíthatjuk ki az energiát:

E_nπ = m_nc² + p_nc

Az összefüggés lehetőséget ad, hogy a neutrínók három típusának megbecsüljük sajátenergiáját, feltételezve, hogy az elektron típusú részecskék kinetikus energiája elhanyagolható. A W bozon eltűnése után visszaáll az eredeti energia (helyreáll az energia-megmaradás szokásos törvénye, amely nem veszi figyelembe a tér potenciális energiáját), ezért az határozza meg, milyen részecske szabadul ki a W bozonból, hogy melyik saját energiája van közel a félfordulatok E_nπ értékéhez. Mivel a tau részecske energiája 1,77682 GeV, azaz E_π fele, így ez a részecske a W bozon első félfordulatánál jöhet létre, ekkor a tau neutrínóra jutó energia maximum 1,697 GeV lehet, tehát a két képződő részecske közel egyformán osztozik a bozon E_π energiáján. A müon saját energiája 105,658 MeV, ezért ez már egy teljes fordulat után jön létre, a müon neutrínóra jutó energia pedig 44,44 MeV lesz, tehát kisebb, mint a müon saját energiája. Végük az elektron, melynek sajátenergiája 0,511 MeV, a harmadik félfordulat után jön létre, és ekkor a neutrínóra marad az energia nagyobb hányada: 5,976 MeV. A nagyságrendi változásból látható, hogy a tau, müon és elektron tömege azonos ütemben csökken a W bozon félfordulatainak energiaveszteségével. A harmadik félfordulat a W bozon utolsó „kijárata”, mert az elektron stabilis részecske és spontán módon nem bocsát ki újabb W bozont. A háromfajta neutrínóhoz rendelt sajátenergia nem konvertálható nyugalmi energiává, valójában nyugalmi tömegük nulla, és ezért képesek a mérések szerint fénysebességgel mozogni. Van viszont a neutrínóknak saját impulzusuk, ami magyarázza, hogy hogyan jöhet létre oszcilláció a különböző típusú neutrínók között. A neutrínók hullámtermészete miatt a hullámhosszúság megadható az impulzusból: λ = h/p, melyek különböző hosszúságúak a három generációban, és összelebegésük hozza létre az oszcillációt. (Antal Rockenbauer: Consequent Quantum Mechanics by Applying 8-Dimensional Spinors in the Dirac Equation; Physical Science International Journal 24, 27-31, 2020.)

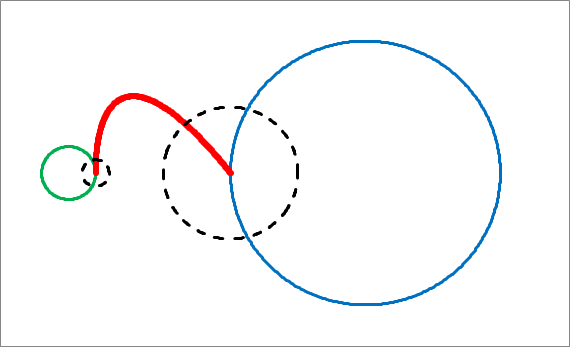
Az ábra szemlélteti a müon (zöld kör) átalakulását elektronná (kék kör) a W^- bozon (piros vonal) közvetítésével két neutrínó (fekete szaggatott vonalú körök) kibocsátása mellett. Megjegyzés: a körök nagyobb sugara a kisebb tömeget jelképezi.

Hadronok bomlása

Leptonok bomlásánál lényegesen bonyolultabb a kvarkokból felépülő mezonok (kvark + antikvark) és a barionok (három kvark, vagy három antikvark) bomlási mechanizmusa. Ennek egyrészt azaz oka, hogy a kvarkok a hadronok belsejében nincsenek sem tömeg, sem impulzus sajátállapotban, amelyben jól definiált sajátértékkel rendelkeznének, másrészt az összetett hadronokban (ez a barionok és mezonok összefoglaló neve) az erős és az elektromágneses kölcsönhatás is fontos szerepet játszik a gyenge-kölcsönhatás mellett. A kvarkoknak két típusa van a 2/3e töltésű u, és a –1/3e töltésű d, és a leptonokhoz hasonlóan három generációjuk létezik, melyek csak tömegükben különböznek (pontosabban renormált tömegükben, mert szabad kvark nem figyelhető meg). Az u típus két magasabb generációja a c és a t kvark, a d típusé az s és a b nevű kvark. A kvarkok három generációjának renormált tömege nagyságrendileg igazodik a W bozon három aktív állapotához: u és d az E_3π, c és s az E_2π, míg b az E_π energiával összemérhető nagyságú. Kilóg a sorból a t kvark, amelynek nagy tömege meghaladja a W bozonét, evvel függhet össze, hogy olyan hadron nem is létezik, amelynek t kvark lenne az egyik összetevője.

Béta-bomlás

Hadronok közül az számít kivételnek, amelyben a gyenge-kölcsönhatás hozza létre a bomlást, ennek oka, hogy az elektromágnesesség által előidézett bomlás ennél 10 nagyságrenddel gyorsabb. Ezért amikor a két kölcsönhatás együtt játszik szerepet, a gyenge-kölcsönhatás részesedése nem becsülhető meg. Barionok közül a két nukleon (proton és neutron) különösen stabil: a proton (uud) spontán módon nem is bomlik fel, csak neutrínó-, vagy gamma-sugárzással alakítható át, míg a neutron (udd) bomlásának felezési ideje rendkívül hosszú: 880 s. A proton stabilitását az okozza, hogy a barionok közül ez a legkisebb saját energiával rendelkező részecske, neutron pedig azért stabilis, mert az elektromágneses kölcsönhatás nem idéz elő spontán bomlást. Ennek oka, hogy a gamma-sugarak nem rendelkeznek töltéssel, és így más részecskék töltését sem változtathatják meg, legfeljebb részecske-antirészecske párokat hozhatnak létre, ha elég nagy az energiájuk. A neutron spontán béta-bomlásakor proton jön létre, amelyet elektron és (anti)neutrínó kibocsátása kísér, más részecskék nem léphetnek ki, mert a neutron és proton közötti 1,3 MeV energiakülönbség nem elegendő müonok létrehozásához.  A béta-bomlás tehát kvark-kvark átalakítási folyamat W^– bozon közvetítésével:

u → d + W^–→ d + e^– + ν_e

Mezonok bomlása

A mezonok családjában az ud összetételű (az aláhúzás jelöli az antikvarkot), +e töltésű pion a legstabilabb, melynek tömege 139,6 MeV/c², a legkisebb a mezonok közül. Ez a tömeg egyrészt összemérhető a W bozon E_2π energiájával, másrészt nagyobb a müon tömegénél, ami magyarázza a kvark kombináció átalakulását müonra és neutrínóra:

ud → W⁺ → μ⁺ + ν

Ekkor a gyenge-kölcsönhatás a kvark-antikvark kombinációt alakítja át leptonokra. Hasonló bomlási folyamata van az us összetételű +e töltésű kaonnak is, ahol a 493 MeV sajátenergia szintén elegendő müon részecske generálásához.

Elektronbefogás

Szintén a gyenge-kölcsönhatás hozza létre az elektron, vagy más néven K befogást. Az atomokban kötött elektron, amikor nulla impulzusnyomatékú „ s” pályán tartózkodik, véges valószínűségsűrűséggel  jelen van az atommag belsejében is, még pedig anélkül, hogy a végtelenül nagy vonzóerő képes lenne befogni az elektront. Ha azonban az atommagban van egy többlet proton a stabilis izotóphoz képest, akkor a gyenge-kölcsönhatás már előidézheti a proton átalakulását elektronbefogás révén. Ekkor az atom rendszáma lecsökken. Példaként nézzük a ²⁶Al atommagot! Ebben 13 proton és 13 neutron van, viszont a stabilis ²⁷Al izotópban már eggyel több a neutron. Az elektronbefogás miatt eggyel csökken a protonok, és eggyel nő a neutronok száma, és létrejön a ²⁶Mg izotóp. Ez annak felel meg, hogy a gyönge-kölcsönhatás az egyik u kvarkot átalakítja d kvarkká W⁺ bozon közvetítésével, amelyik a második lépésben elnyeli az elektront:

u + e^– → d + W⁺ + e^– → ν_e + d

(Itt a töltésmegmaradást az biztosítja, hogy u töltése 2/3e, míg d töltése -1/3e.) A rádióaktivitásnak ez a típusa eltér a szokásos bomlásoktól, mert ha megfosztjuk az atomokat az elektronoktól (teljes ionizáció), akkor nem jön létre az atommag átalakulása, azaz nem lesz többé radioaktív a szóban forgó izotóp.

A Z bozon színre lépése

A gyenge-kölcsönhatás olyankor is megfigyelhető, amikor nem történik részecskeátalakulás. Buborékkamrában vizsgált elektronoknál azt tapasztalták, ha jelentős neutrínó fluxus halad át a kamrán, egyes elektronok mozgása hirtelen megváltozik (Carlo Rubbia, Simon van der Meer, Nobel díj: 1984). Ezt úgy lehetett értelmezni, hogy az elektron lökést kaphat a neutrínóktól, amit viszont csak egy új kölcsönhatás idézhet elő, hiszen gammasugarak nem voltak jelen. Mivel az elektronok töltése változatlan maradt, a jelenség semleges bozon jelenlétére utalt, amelyet Z bozonnak neveztek el. Ennek tömege 91,2 GeV/c² a mérések szerint, amely még a W bozonét is meghaladja. A szakirodalom a folyamatot rugalmas neutrínó szórásnak nevezi, amely az jelzi, hogy a folyamatban nem alakul át a meglökött elektron más részecskévé.

Itt érdemes arra gondolni, hogyan tudja az egyik test meglökni a másikat, amikor nekiütközik? Számunkra ez természetesnek tűnik, pedig ez a lökés nem jöhetne létre elektromágneses kölcsönhatás nélkül!. A neutrínó például nem rendelkezik elektromos töltéssel, ezért bár óriási számban áramlik a Napból, annak hatását nem vesszük észre, és veszteség nélkül halad át az egész Földgolyón! A fénysebességű forgásmodell úgy értelmezi a Z bozont, mint két ellentétes kiralitású spirális szuperpozícióját. A W bozonhoz hasonlóan a semleges Z bozon tömegénél fogva rendelkezik impulzussal, és ezt ütközéskor átadhatja az elektronoknak, mert létrejön közöttük a gyenge-kölcsönhatás.

Ez az írás az 2017 április 3.-i bejegyzés (Látogatás az elemi részecskék szerelőműhelyében: gyenge-kölcsönhatás) átírt változata.

További írások a blogon: Paradigmaváltás a fizikában.

A pontszerűség mellett szóló érvek

Pontszerű-e az elektron? Bizonyos kísérletek szerint igen! Erre adnak példát a Bhabha kísérletek. Bombázzunk elektronokat pozitronokkal! A találkozáskor a két részecske gamma sugárzás kíséretében annihilál. Könnyebb egy térben kiterjedt töltésrendszert eltalálni, ha annak mérete nagy. A nagy energiájú szóráskísérletek azonban azt mutatják, hogy nagyon kicsi a találati valószínűség, és a mérési pontosság határain belül nulla az elektron töltéseloszlásának sugara. Más részecskéknél ez nem így van, így derítették fel különböző szórásvizsgálatokban a proton és neutron töltésének véges térbeli eloszlását.

Más jelenségekkel is összhangban van a pontszerűségi elv: az elektront ugyanis nem lehet kisebb egységekre felbontani. A felbonthatatlanság természetesen biztosan teljesül, ha tényleg pontszerű egy részecske, de ez önmagában még nem bizonyíték a pontszerűség mellett, mert a felbonthatatlanságnak más oka is lehet.

Ellenérvek a pontszerűséggel szemben

Más oldalról, milyen érvek hozhatók fel a pontszerűség ellen? Mindenekelőtt feltehető a kérdés, hogy lehet-e bármilyen fizikai objektum végtelenül kicsi, felbontható-e az anyag végtelenül apró darabokra? Itt lép be a démokritoszi atomelv, amelynek álláspontja szerint, kell lenni valahol egy oszthatósági határnak, még ha mai tudásunk szerint ez a határ nem is az, amit ma atomnak nevezünk, sőt az atommag is felbontható nukleonokra (proton és neutron), de még ez sem a végső felbontási határ, hanem annak is vannak kisebb elemei: a kvarkok. Ismereteinket összegző Standard Modell szerint, a már tovább nem bontható elemi objektumok az említett kvarkok, de ide tartoznak még a fermionok közül az elektron és neutrínó család tagjai, valamint a különböző kölcsönhatásokat közvetítő bozonok, jelesül a fotonok, a W és Z részecskék, és a gluonok. A kérdés persze fennmarad, biztosak lehetünk-e abban, hogy amit ma a fizikai világ legapróbb építőköveinek tartunk, nem oszthatók-e mégis tovább, lehet, hogy ezek is valamilyen folytonos anyagból épülnek fel? Ha persze az elektron tényleg pontszerű, lezárhatjuk a kérdést, hiszen a pont az a végső matematikai határérték, amely megfogalmazza a felbonthatatlan kiterjedés nélküliséget.

Ami azonban leginkább szembemegy a pontszerű elektron felfogásával, hogy az elektron olyan fizikai tulajdonságokkal rendelkezik, amely csak térben kiterjedt testeknek lehet: ezek a nyomatékot (momentumot) kifejező fizikai mennyiségek, jelesül az impulzus- és a mágneses nyomaték. Az előbbi arra utal, mintha az elektron tömege véges tértartományt foglalna el, az utóbbi szerint ez vonatkozik az elektron töltésére is.

Az ellentmondás feloldása fénysebességű forgásokkal

Lehet-e egyáltalán olyan fizikai objektum, amely két ilyen egymásnak ellentmondó tulajdonsággal rendelkezik? Ha a részecskékhez fénysebességű forgásokat rendelünk, akkor igen! Ennek magyarázatát a relativitáselmélet Lorentz transzformációja adja meg. Ha hozzánk képest egy test valamilyen sebességgel mozog, annak méretét a mozgás irányában kisebbnek látjuk, és ha elérjük a fénysebességet, akkor a méret nullára zsugorodik. De ez csak a mozgás irányára igaz, mert a mozgásra merőlegesen a méret ugyanakkora marad. Képzeljünk el egy R sugarú fizikai objektumot, álló esetben a kerület hossza 2Rπ. Kisebb lesz azonban a kerület hossza, ha forogni kezd a test ω = f/2π körfrekvenciával, és ha eléri a v = ωR kerületi sebesség a c fénysebességet, akkor a kör kerülete már nullára zsugorodik. De mi lesz a sugárral? Mivel a sugár mindig merőleges a mozgásirányra, ez változatlanul R értékű marad. De lépjünk tovább és képzeljünk el egy olyan forgást, amelyik egyszerre két egymásra merőleges tengely körül megy végbe, ez már egy gömb felületét futja be. Ennek a gömbnek a felülete a kívülálló számára már nulla lesz 4R²π helyett, de sugara változatlan marad.

A tömeg és az impulzusnyomaték eredete

A tömeggel azonban bajban vagyunk, ugyanis véges tömeg nem mozoghat fénysebességgel, mert a c sebesség miatt ez végtelenül nagy lenne a relativitáselmélet szabályai szerint. Fordítsuk ezért meg a gondolatmenetet, és tegyük fel, hogy épp a c sebességű mozgás felelős a tömeg létrehozásáért! Ez a forgó test legyen tehát az üres tér lokális tartománya, amelynek nincs is tömege, de ez a nulla tömeg matematikai határértékként viselkedik. A határérték számítás szabálya szerint, ha egy nullához tartó függvény értékét végtelenhez tartó számmal szorzunk, akkor a szorzat felvehet véges értéket is! Alapul véve a Lorentz törvényből fakadó tömegnövekedési szabályt, amely szerint c sebességnél a tömeg végtelenszer nagyobb lesz, majd szorozzuk meg ezt a végtelenhez tartó számot a nulla határértékű tömeggel, akkor eljuthatunk a részecske véges tömegéhez. Ez a gondolatmenet a fénysebességű forgás koncepciója, amely feloldja az ellentmondást a szóráskísérletekben pontszerűként viselkedő elektron és a véges impulzusnyomaték létezése között. Ez a koncepció új funkciót ad a térnek, amely többé nem passzív tartály, amelyben a részecskék világa elhelyezkedik, hanem a részecskék megalkotója is. A térben minden mozgás sebessége relatív, de van egy nagy kivétel: a fénysebesség, amely a relativitáselmélet szerint mindig azonos vákuumban. Akár hozzánk közelítő, vagy távolodó objektum bocsátja ki a fényt, mindig azonos sebességgel teszi meg felénk az utat. Ezért a fénysebességet mint a tér szerkezeti állandóját foghatjuk fel. Ha a térben valamilyen ω körfrekvenciával forgás alakul ki, az kijelöl egy véges tartományt a térben, amelynek sugarát az R = c/ω szabály adja meg. Fogjuk úgy fel a fotont, mint a tér forgását, rendeljük hozzá az ω körfrekvenciához az E = ћω energiát, és a tömeg-energia ekvivalencia alapján adjuk meg az m = E/c² relativisztikus tömeget is. Foton esetén ez a tömeg nincs nyugalomban, mert a fény természeténél fogva c sebességgel száguld. Így a foton nem lehet nyugalomban, így nyugalmi tömege sincs, van viszont relativisztikus mozgási tömege! Ennek a tömegnek szorzata a fénysebességgel már mérhető mennyiséghez: az m·c impulzushoz vezet, amit ha megszorzunk a sugárral, megkapjuk a foton impulzusnyomatékát. A számítás eredménye épp azt a ћ = h/2π impulzusnyomaték, amit annak idején Planck megállapított! Még arra is választ kapunk, hogy bár a foton frekvenciája és energiája rendkívül széles határok között változik, az impulzusnyomaték mégis pontosan ugyanakkora marad.

De térjünk rá a kettős forgással értelmezett elektronra. Itt a gömbfelület zsugorodik nullára a fénysebességű forgás miatt, ez tükröződik a Bhabha kísérletben is. A kettős forgást úgy foghatjuk fel, hogy először egy kiválasztott tengely körül 2π szögű forgatást végzünk el, majd ezt egy erre merőleges tengely körül megismételjük, azaz összességben 4π szögű forgatást hajtunk végre. Ennek a gömbforgásnak frekvenciája az egyetlen tengely körüli forgáshoz képest fele akkora lesz: Ω = ω/2. Ezt a gömbfrekvenciát hozzuk kapcsolatba a részecske tömegével: mc² = ћΩ. Az impulzusnyomaték komponenseit úgy kapjuk meg, ha az egyes tengelyek körül az ω körfrekvenciát vesszük figyelembe, ahol most ω = 2mc²/ ћ. Ezt behelyettesítve az impulzusnyomaték kifejezésébe kapjuk, hogy m·c·r = ћ/2. Így jutunk el az S = ½ spinhez, amelyik minden elemi fermion sajátja bármekkora is a tömeg. Spinnek nevezzük a ћ egységben megadott impulzusnyomaték együtthatóját, ez fotonoknál S = 1, az elektronnál S = ½ értéket vesz fel. Más részecskéket is a spinnel jellemezzük, amely bozonoknál S = 1 és fermionoknál  S = ½. Összetett szerkezetű részecskéknél ezt úgy általánosítják, hogy a spin bármely egész szám lehet bozonoknál, és bármely „félegész” fermionok esetén.

Centrifugális erő és az erős gravitáció

Ha egy m tömegű test ω körfrekvenciával kering egy R sugarú körön, akkor arra F_C = mω²R centrifugális erő hat. Emiatt felvetődik a kérdés, hogy milyen erő képes stabilizálni a forgást a szétrepítő erő kiegyenlítésével? (Lásd: Rockenbauer Antal: „A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója, Scolar Kiadó, 2017, pp. 53-55). Helyettesítsük be a centrifugális erő képletébe az előzőekben alkalmazott összefüggéseket, ekkor a fénysebességű forgás centrifugális ereje F_C = ћc/R² lesz. Az ellensúlyozó erő megtalálásához forduljunk az általános relativitáselmélethez, amely a tér görbületével magyarázza a gravitációs erőt. Tételezzük fel, hogy a részecskét alkotó kettős forgás „kilép” a zárt tartományból, és frekvenciája követi a Kepler-Newton törvényt, amely szerint ω²r³ = konstans az r > R tartományban. Ennek a forgásnak a v = ωr kerületi sebessége bármely elemi részecske esetén sok nagyságrenddel kisebb a fénysebességnél, és csökken a távolsággal. A Lorentz-kontrakció szabálya szerint a kör kerülete a v/c aránytól függően lecsökken, és ezt a csökkenést vehetjük a térgörbület mértékének. A görbület mértékéből definiálva egy erőt, reprodukálhatjuk a Newton-féle gravitációs törvényt. Most alkalmazzuk ezt a formulát arra az esetre, amikor a részecske felületén a fénysebesség miatt a kerület hossza nulla lesz. Ekkor arra az eredményre jutunk, hogy ott a gravitációs erő épp ћc/R², azaz a gravitáció (ezt nevezzük erős gravitációnak) éppen kiegyensúlyozza a centrifugális erőt. A fénysebességű forgás modellje szerint tehát nem kell kívülről energiát igénybe venni a részecskék mc² nyugalmi energiájának biztosításához, mert ezt az extrém módon görbült tér potenciális energiája biztosítja. A részecskék „képződéséhez” tehát nem kell energia, csak az impulzusnyomaték forrását kell biztosítani. Evvel magyarázatot kapunk arra is, hogy a béta-bomlás folyamatában, amikor a neutron protonná alakul át egy elektron és egy neutrínó kibocsátásával, hogyan képződhet olyan közvetítő bozon (W bozon), amelynek tömege közel százszor nagyobb a kibocsátó neutronhoz képest.

Az elektron anomális mágneses nyomatéka

Az elektronok véges mágneses nyomatékkal is rendelkeznek, melyet a relativisztikus Dirac-egyenletből lehet származtatni:

    M_S = 2μ_BS,

ahol μ_B = eћ/2mc a Bohr magneton. Ezt származtatni tudjuk fénysebességű forgással, ha az e elemi töltés körforgását vesszük alapul, és a mágneses nyomaték számításánál alkalmazzuk az elektrodinamika M = IF/c törvényét, ahol a töltés árama I = e·f = eω/2π, a kör területe F = R²π. A behelyettesítések után kapjuk, hogy:

M_S = eR/2 = μ_B = 2μ_BS

Az elektronok pályamozgása esetén, ha a pálya-impulzusnyomatéka Lħ, a megfelelő képlet: M_L = μ_BL. Miért lép fel a 2-es szorzó a spin járulékában? Ennek megválaszolásával a fizika már régóta küszködik. A kettős forgás koncepciója azonban kézenfekvő magyarázatot ad a kérdésre. A spint a kettős forgásból származtatjuk, viszont a mágneses nyomaték a mágneses mező körüli Larmor-precesszióból ered. Ez a forgás viszont egy tengely körül történik, amiért nem lép fel az impulzusnyomaték számításnál alkalmazott feleződési szabály.

A mágneses nyomaték azonban nem pontosan egyenlő a Dirac-egyenletből származtatott értékkel, hanem kissé nagyobb:

 M_S = 2,002319304μ_BS

Mi okozza ezt a növekedést? A kvantum-elektrodinamika (QED) mezőelmélete erre rendkívül pontos megoldást ad különböző szintű közelítések keretében. A QED alapgondolata, hogy az elektromos töltések vonzó-taszító hatását virtuális (közvetlenül nem detektálható) fotonok hozzák létre, amelyek állandóan kibocsátódnak és elnyelődnek, amely így fluktuációt okoz a részecske pozíciójában, és ez megnöveli a mágneses mező nagyságát. A nehézveretű elmélet helyett a fénysebességű modellel is magyarázatot adhatunk a legfontosabb tagra.

A részecske belső tartományából való foton kibocsátást a kettősforgás által kiváltott és ћc/R² amplitúdójú Coriolis-erő oszcillációja okozza (lásd: Pillantás az elemi részecskék belsejébe: kvarkok és gluonok különös világa). A foton kilépésekor ez az erő csillapodik az α = 1/137,036 Sommerfeld-állandóval, amely az e² = α ћc összefüggésben realizálódik. Ennek megjelenése hozzáadódik a centrifugális erőhöz, de amíg a centrifugális erő a teljes körön egyenletesen hat, itt a kilépés mindig valamelyik irányban megy végbe, amit a 2π-vel való osztás vesz figyelembe. A megnövekedett kifelé ható erőt már a valamivel erősebben görbült tér tudja kiegyenlíteni, ezért kisebb lesz az erős gravitációt okozó R_G görbületi sugár a centrifugális erő R_C sugarához képest:

ћc/R_G² = ћc/R_C² + (α/2π)ћc/R_C²

Innen kapjuk a töltés által körüljárt felület megnövekedését:

R_C²/R_G² = 1+ α/2π

Ez az arány jelenik meg az elektron anomális mágneses nyomatékának első korrekciós tagjában. (Bár a mágneses nyomaték lineárisan függ a részecske sugarától, mégis a felülettel való arányosság határozza meg a korrekciót, mert a tömeget létrehozó ω = c/R körfrekvencia azonos marad.) A számítás tovább finomítható, ha figyelembe vesszük, hogy a korrekció miatt csökken az elektron belső terének energiája 1 - α/2π mértékében:

R_C²/R_G² = 1+ ∝/2π(1 - α/2π)

Ekkor a mágneses nyomaték már csak a hetedik tizedes jegyben tér el a kísérleti adattól:

M_S = 2,002320104μ_BS

Szemléletesen úgy is fogalmazhatunk, hogy az elektronnak kettős héja van: a belső felülete határozza meg a tömeget és az impulzusnyomatékot, a külső a fluktuációs mozgás miatt alakul ki, amiben a belső gömb „lötyög”, és ezáltal megnöveli a töltés által bejárható nagyobb felületet.

Miért lesz végtelen az elektron sajátenergiája a QED elméletben?

A QED elmélete látványosan szép eredményre vezet az elektron anomális mágneses nyomatékának meghatározásával, mégis van egy súlyos hibája: a sajátenergia első perturbációjának számítása végtelenül nagy értékre vezet. Ha ezt önkényesen elhagyjuk, akkor a további tagok rendkívül nagy pontossággal adják vissza a kísérleti értéket. Az elméletnek ezt a gyenge pontját a klasszikus elektrodinamikától örökölte, amikor számba vette az elektron elektromos kölcsönhatásának sajátenergiáját. Ezt úgy végzik el, hogy az elemi töltést végtelenül kis elemekre bontják fel, és először elviszik ezeket a töltéseket végtelen távolságba, majd kiszámítják a munkavégzést, amikor a töltést egyetlen pontba egyesítik. Az alkalmazott módszer eleve ellentmondáson alapul, amikor felbontja az oszthatatlan elemi töltést. A végtelen sajátenergia pedig onnan származik, hogy az integrálást nulláig viszik, mintha tényleg egyetlen matematikai pontban lenne a töltés, ahol már a taszítási erő ellen végzett munka végtelenül nagy. A QED elmélete is a kölcsönhatást nulláig kiterjesztett integrálokkal írja fel, ezért jelenik meg ott is a szingularitás. Ezt a hibát kiküszöböli a fénysebességű forgás koncepciója, amely véges sugarat határoz meg a részecske számára. Az elektromágneses mező energiája a részecske által a belső tartományból a külső térbe kiküldött hányad, amit az α Sommerfeld-állandó ad meg, míg az mc² sajátenergia döntő hányada (1 – α = 0,9927-ed  része) belül marad. Helytelen ezért az olyan próbálkozás is, amely az elektromágneses mező energiájával akarja értelmezni a teljes sajátenergiát (lásd: klasszikus elektronsugár).

Anyag és antianyag a fénysebességű forgásokban

Az elmondottakon kívül a fénysebességű forgásmodell kézenfekvő magyarázatot ad az anyag és antianyag, illetve a pozitív és negatív elektromos töltés eredetére is. Ez a kettős forgás szimmetriájára vezethető vissza, amely lehet jobb és balsodrású is. Ez a szimmetria a háromdimenziós tér sajátja. A korábbi írásban (Pillantás az elemi részecskék belsejébe: kvarkok és gluonok különös világa) azt is kimutattuk, hogy mi a töltés eredete, és hogyan lehet a kvarkoknak 2/3e és 1/3e töltése is a forgás jellegétől függően. Itt csak azt kívánjuk leszögezni, hogy a fénysebességű forgásmodell alkalmas az egész részecskevilág leírására, azon túlmenően, hogy feloldja a látszólagos ellentmondást az elektron pontszerűsége és a fizikai nyomatékok létezése között.

Összetett részecskék spinje és a véges hatáskeresztmetszet

A pontszerűséggel kapcsolatban érdemes még kitérni arra a kérdésre is, hogy a proton töltéseloszlása a mérések szerint nem pontszerű, bár az elektronhoz hasonlóan a spinje ½. Az elektron impulzusnyomatékát a fénysebességű kettős forgásra vezettük vissza, ezért ha evvel magyaráznánk a proton spinjét is, akkor nulla hatáskeresztmetszetet várnánk proton esetén is a szóráskísérletekben. Ha nem tudnánk már az elméletből, hogy a proton három kvarkból épül fel, akkor már a véges hatáskeresztmetszet létezéséből levonhatnánk a tanulságot, hogy a proton összetett szerkezetű! Mivel a valóban elemi fermionoknak a kettős forgás koncepciója szerint ½ a spinje, így a spinek összeadási szabályából már következik, hogy legalább három komponensből épül fel a proton, ugyanis két ½ spin összege nulla, vagy egy lehet. Egyébként az összetett részecskék családjában vannak két kvarkra bontható mezonok is, ahol tényleg a spin 0, vagy 1 értéket vesz fel. Három ½ spin alkothat akár ½, akár 3/2 spint is. Léteznek ennek megfelelően olyan barionok is, melyeknek spinje 3/2. (Barionnak nevezzük a három kvarkból, vagy antikvarkból felépülő részecskéket, ennek legstabilabb két tagja a proton és a neutron).

Folytonosság, pontszerűség és diszkrét energiák

Hogyan kapcsolódik a részecskék pontszerűségének cáfolata a fizikai világ folytonosságának kérdéséhez? Az energia estén látszólag megszűnik a folytonosság, hiszen az atomban kötött elektronok diszkrét energiájúak, és adott frekvenciájú fény energiája is E = h·f nagyságú lépcsőkben változik. Fölvethető emiatt, vajon a tér és az idő se lenne folytonos? Nézzük először a klasszikus fizikát! Minden területen a folytonosságból indul ki, és differenciálegyenletekkel írja le törvényeit, akár mechanikáról, elektromágnesességről, vagy termodinamikáról van szó. Ez a szemléletmód abból indul ki, hogy – legalább is elvben – a mozgásokról folytonosan érkezik az információ a folytonosan érkező fény miatt. Gyakorlati szempontból ez a matematikai technika rendkívül hasznos, mert a végtelenül kis változások birodalmában lineárissá válnak a legbonyolultabb összefüggések is, ami nagyon megkönnyíti a számításokat. A nehézség mindig az integrálásoknál következik be, amikor makroszkopikus méreteket vizsgálunk.

Jelenlegi kvantumfelfogásunk szerint sem beszélhetünk kvantált térről, vagy időről. Ennek oka, hogy a kvantummechanika operátorait az idő és a térkoordináták szerint differenciálhányadosok adják meg, már pedig ez megköveteli, hogy a koordinátákat végtelenül kis elemekre tudjuk felbontani, és folytonosnak kell lenni az állapotfüggvénynek is. De mégis hol az a pont, ami kvantumok kialakulásához vezet? Ez a körmozgás, amelyben a szögkoordináta 360 fokonként visszatér önmagába, ez az önmagába való visszatérés vetítődik ki az anyag periodikus hullámaiban is. Klasszikusan a mozgás pontról pontra követhető, mert elvben tetszés szerinti kis távolságban és időközben érkeznek hozzánk a fotonok, de ez már nincs így a kvantumok világában, mert a stacionárius állapotban „néma” az elektron, nem bocsát ki, vagy nyel el fotont, kizárólag csak a különböző állapotok közötti ugrásokat látjuk. Ha ebből visszakövetkeztetünk az elektronpályákra, az csak az egész pályáról, azaz a teljes körforgásokról adhat információt. Ez az információ a pálya impulzusnyomatéka, amit a redukált Planck-állandó egész számú többszöröse ad meg. Miért kötelező, hogy ez így legyen, miért nem keringhet tetszésszinti pályán az elektron? Ennek oka, hogy az elektron kötőpályára jutását a fotonok segítik elő. A szabadon mozgó elektronnak nincs pálya-impulzusnyomatéka, amikor azonban az atommag közelébe kerül, a vonzás gyorsítást, ez pedig foton kibocsátást okoz, de minden ilyen kibocsátás alkalmából ћ egységnyi impulzusnyomaték változás következik be. Végül, amikor kialakul a kötött stacionárius állapot, egész számú lépés határozza meg, hogy milyen impulzusnyomaték tartozik a landolási pályához.

De hol lép be a kvantummechanikai formalizmusba, hogy az állapotfüggvény által meghatározott impulzusnyomaték csak ћ egész számú többszöröse lehet? Ezt az garantálja, hogy az energia, impulzus és impulzusnyomaték operátoraiban ott szerepel a ћ konstans mint a differenciálhányadosok együtthatója. Az impulzusnyomaték J_z = iћδ/δφ komponense a tengely körüli forgás poláris szögével képzett differenciálhányados, viszont a szög 360 fokos elfordulás a kezdő állapotnak felel meg. Ennek matematikai következménye, hogy az operátor sajátfüggvénye periodikus lesz, és a belső ismétlődések száma adja meg a kvantumszámokat.

További bejegyzések: "Paradigmaváltás a fizikában"