Milyen fizikai nyomatékok vannak?

A klasszikus fizika fontos fogalma a nyomaték és komoly szerepet játszik mindennapjainkban is. A nyomaték különböző formáiról beszélünk, ilyen a forgatónyomaték, az impulzus és a mágneses nyomaték, de van nyomatéka a tömegnek is, amit tehetetlenségi nyomatéknak nevezünk. Szintén megjelenik a nyomaték fogalma a mikrovilágban, amit elterjedten neveznek momentumnak is, amikor a legkisebb elemi objektum fizikai paramétereit adják meg. A momentum fizikai definíciója és dimenziója azonos a nyomatékkal, ezért felmerül a kérdés, vajon csak szóhasználati kérdésről van szó a klasszikus és a kvantummechanika között, vagy a két fogalom között átjárhatatlan szakadék van?

Spin: az elemi objektumok közös attribútuma

 Mindenekelőtt beszélnünk kell az elemi részecskéket jellemző spinről, azaz az impulzusmomentumnak ℏ redukált Planck állandó egységében megadott együtthatójáról. Akár a tömeg, akár az elektromos töltés hiányozhat az elemi részecskék meghatározó tulajdonságai közül, de spinnel valamennyi rendelkezik, így a fény kvantuma a foton, az elektron és a neutrínó, az atommagokat felépítő protonok és neutronok, sőt az ezeket alkotó kvarkok is és még sorolhatnánk.

A klasszikus és kvantummechanika összekötő kapcsa: a korrespondencia elv

De van-e kapcsolat a makro- és a mikrovilág nyomaték, illetve momentum definíciója között? A kvantummechanika egyes fogalmait, következtetéseit a józanész gyakran nehezen tudja elfogadni, de van egy megnyugtató elv, a korrespondencia. Ez arra utal, hogy amikor számtalan mikrorészecske együtteséről van szó, akkor a kvantummechanika törvényei belesimulnak a klasszikus fizika szabályaiba, mert a kvantum „lépcsői” már olyan parányiak, hogy a megfigyelő számára észrevehetetlenné válnak. Erre alapozva gondolatmenetünket induljunk ki a nyomaték hétköznapok fogalmi rendszeréből, majd térjünk rá a mikrovilág objektumainak sajátságos világára.

Nyomatékok a hétköznapi világban

A nyomatékkal találkozunk hétköznapjainkban is, amikor a ruhát feltesszük a fregolira száradni. A felfüggesztéssel párhuzamosan helyezkednek el zsinórok különböző távolságra a felfüggesztéstől és ha a ruhadarabot valamelyik távolabbi zsinórra tesszük, az jobban forgatja lefelé az egyik oldalt, mintha közel tennénk. Ennek megfelelően, ha az egyes darabok súlya különbözik, azt kiegyensúlyozhatjuk, ha a nagyobb súlyt helyezzük közel a felfüggesztéshez és a kisebbet távolabbra. Ezt úgy fogalmazza meg a fizika, hogy a forgató erő fogalmát kiegészíti a forgatónyomatékkal, amelyben a súlyon kívül a forgás tengelyétől való távolság is figyelembe van véve. Ha pontos matematikai összefüggéshez akarunk jutni, akkor egy vektort rajzolunk a tárgy helye és a forgástengely közé, majd egy másikat, amelyik az erő irányát mutatja és ezek vektoriális szorzata jellemzi a nyomaték nagyságát:

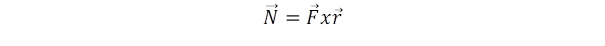
(A vektoriális szorzat nagyságát a két vektor által kijelölt háromszög területe adja, iránya pedig mindkét vektorra merőleges. Ez a harmadik irány mutathat felfele, vagy lefele, ez a jobb- illetve balkezes sodrásirány. Ennek megfelelően adhatunk a forgatónyomatéknak pozitív, vagy negatív előjelet.).

A forgatónyomaték szerepe az egyszerű gépeknél

A forgatónyomaték magyarázza sok egyszerű gép erőátviteli szabályát, úgyszintén fontos a szerepe a kétkarú mérlegek esetében, vagy amikor a motor erejét kerekek forgatására használjuk fel. De gondolhatunk a kerekes kútra is, amikor vizet húzunk fel a kútból. Két dolog a lényeges: egyrészt mekkora a sugár, ami átviszi az erőt, másrészt a forgató erő ne változtassa meg a tárgy alakját, azaz merev legyen.

Tömeg: a test tehetetlensége

A nyomaték másik megnyilvánulását a test tömegével hozhatjuk kapcsolatba. A Newton törvény szerint a test tömege, azaz a tehetetlensége határozza meg, hogy mekkora erő kell a test felgyorsításához. Ez a törvény az impulzusváltozás segítségével is megfogalmazható (az impulzus egyenlő a tömeg és a sebesség szorzatával:  ,)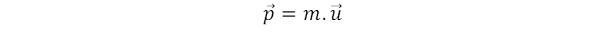

A test impulzusváltozása pedig a ráható erővel egyenlő:

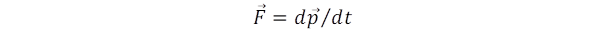
: . Ebből az is következik, ha a testre nem hat külső erő, akkor impulzusa állandó marad. Érdemes megjegyezni, hogy az erő és impulzus kapcsolata általánosabb, mint Newton eredeti megfogalmazása az erő és a gyorsulás között, mert ez az összefüggés a relativitáselméletben is érvényes.

Mi a tehetetlenségi nyomaték?

A gyorsításhoz hasonló törvény mondja ki, hogyan tudunk egy testet forgásba hozni. Itt a forgás frekvenciája játssza a fő szerepet, azaz a szögsebesség, ami megmondja, hogy egy másodperc alatt hány 360 fokos  fordulatra  kerül sor (a teljes fordulat radiánban 2π). A radiánokban mért szögsebesség a ν frekvenciával kifejezve: ω = 2πν. Ennek a szögsebességnek a változása, azaz a szöggyorsulás, ami arányos lesz a  forgatónyomatékkal:

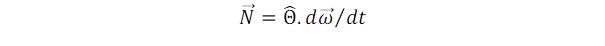
ahol a Θ mátrix jelöli a test tehetetlenségi nyomatékát. Ez a nyomaték arányos a tömeggel, de érzékenyen függ a test méretéről is, például egy labda, vagy karika sugarától. Ez a függés négyzetes, tehát ha veszünk két azonos tömegű labdát, és az egyik sugara kétszer akkora, akkor a tehetetlenségi nyomaték négyszeres lesz. (Bonyolultabb alakú testek esetén ez a tehetetlenségi nyomaték a forgás tengelyétől is függ, amit a 3x3 elemből felépített mátrix ír le. Így például ugyanakkora szöggyorsulást más nagyságú forgatónyomaték hoz létre, ha egy karikát az átlója körül pörgetünk, mintha úgy forgatunk meg, mint egy hula-hoop karikát. A számítást úgy végezhetjük el, ha a testet a forgástengely körül pontszerű darabokra bontjuk és a darabok tömegét a távolság négyzetével szorozzuk, majd az összes pontra elvégezzük az összegzést. A forgástengely mindig a test súlypontján halad át),

Az impulzusnyomaték megmaradási törvénye

Miként az impulzusváltozást kapcsolatba hoztuk a testre ható erővel, hasonló a kapcsolat az impulzusnyomaték változás és a forgatónyomaték között. Az impulzusnyomatékot a forgatónyomatékhoz hasonló vektorszorzat definiálja

:

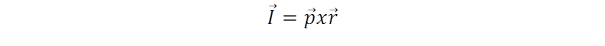
Az impulzusnyomaték egyúttal kifejezhető a tehetetlenségi nyomaték és a szögsebesség szorzatával is:

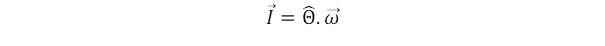
Az impulzusnyomaték változását pedig a forgatónyomaték idézi elő:

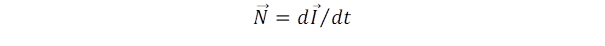
Ez az összefüggés egyúttal az impulzusnyomaték megmaradási törvénye is, mert ha a testre nem hat külső forgató erő, akkor az impulzusnyomaték megmarad. Ezt jól szemlélteti a műkorcsolya piruett figurája: először a táncos kitárt karokkal vesz lendületet, majd karjait szorosan a teste mellé zárja és ezáltal a forgása felgyorsul. Közben ugyanis az impulzusnyomaték nem változik, de a forgást akadályozó tehetetlenségi nyomaték igen. Mivel zárt karok esetén a tehetetlenségi nyomaték jóval kisebb, így a forgás frekvenciája megnövekszik.

Az impulzusnyomaték szerepe a gyakorlatban

Az impulzusnyomaték megmaradásának elvét hasznosítjuk kerékpározás közben is. A gyorsan pörgő kerék impulzusnyomatéka jelentős mértékű, ami függőleges helyzetben tartja a kerékpárt, mert a kidőlés oldalirányú forgatónyomatékot hoz létre, amit viszont ellensúlyozni képes az impulzusnyomaték megtartására irányuló ellenerő. Másik példa a pörgő puskagolyó céltartása. Pörgés nélkül a légellenállás miatt bukdácsolna a golyó, de a pörgés impulzusnyomatéka meggátolja ebben.

Impulzusnyomaték a bolygók keringésében

Az impulzusnyomaték nem csak a testek saját tengelye körüli forgásának, hanem a bolygók, égitestek és műholdak keringő mozgásának is fontos állandója. Körpálya esetén a keringési sebesség és a sugár kapcsolatát a G.M.m/r² gravitációs vonzás (G az általános gravitációs állandó, M a Nap és m a bolygó tömege) és az m.u²/r centrifugális erő egyensúlya határozza meg. Az I = m.u.r impulzusnyomatékot ebből meghatározva kapjuk, hogy

I² = G.M.m².r

Ekkor az impulzusnyomaték megmaradás a bolygók keringési pályájának síkját stabilizálja. Ez a stabilizáló hatás a nagybolygók esetén különösen erős, de gyenge az apróbb égitestek esetén. A klasszikus mechanikában a keringési sugár folytonosan változhat, ezért szintén folytonosan változik az impulzusnyomaték is.

A fény impulzusmomentuma

Az impulzusmomentum – tehát az impulzus nyomatéka – az elemi részecskék alapvető jellemzője és a kvantummechanika legfontosabb kategóriája, akár a kötött állapotok keringéséről, akár az elemi részecskék saját (intrinsic) tulajdonságairól van szó. Kezdjük először a fény kvantumával, a fotonnal, amelyik impulzusmomentum I = S.ℏ, ahol S = 1, amit spinnek nevezünk és ℏ = h/2π a redukált Planck állandó. Az egész értékű spinnel rendelkező részecskéket, így a fotonokat is bozonnak nevezzük. A fotonok energiája, illetve frekvenciája – a kettőt az E = h.ν összefüggés kapcsolja össze – rendkívül különböző lehet, a rádióhullámoktól végig futva a kemény gamma sugarakig a különbség több mint húsz nagyságrendet ölel fel, de a spin, azaz az impulzusmomentum hajszálpontosan megegyezik. A foton ezenkívül impulzussal is rendelkezik p = h.v/c = h/λ összefüggés szerint, ahol λ a foton hullámhossza. Ami zavarba ejtő, hogy ugyanakkor a foton nyugalmi tömege nulla, de honnan származik akkor az impulzusa, ami a tömeg és a sebesség szorzata? A nulla nyugalmi tömeget megköveteli a relativitáselmélet tömegnövekedési szabálya, mert a fénysebességű mozgás a véges tömeget végtelenre növelné meg. Szintén a relativitáselmélet mondja ki az energia és a tömeg ekvivalenciáját az E = m.c² törvény szerint. Úgy tarthatjuk meg ennek érvényességét, ha kétféle tömegről beszélünk, az egyik a nyugalmi, a másik a mozgási tömeg. A tömeg és energia kapcsolatát megadó c² pedig azt jelenti, hogy a nyugalmi tömeg határértékben nulla, de a végtelenbe futó tömegnövekedési szabály ezt végessé teszi, ahogy az 1/X és az X számok szorzata is mindig egy, akkor is ha X a végtelenhez 1/X a nullához közelít. A mozgási tömeg így veheti fel az m = h.ν/c² értéket. Evvel egyúttal arra is magyarázatot kaptunk, hogy honnan származik a foton impulzusa, ami a fénysebesség miatt p = m.c = h.ν/c lesz.

A fénysebességű forgás koncepciója

Hátra van még a legnehezebb feladat, hogy magyarázatot találjunk a foton impulzusmomentumára is. A klasszikus mechanika szerint ehhez kell egyrészt forgás, vagy keringés, valamint az impulzuson kívül még valamilyen sugár is. Gondoljunk a korrespondencia elvre: ha az elemi impulzusnyomatékhoz nem tartozik valamilyen forgás és sugár, akkor a makrovilágban ezek hogyan összegeződhetnének úgy össze, hogy ott a sugár és a forgás megjelenjen? Tételezzük fel, hogy a foton nem csak fénysebességgel halad, hanem ugyanekkora kerületi sebességgel forog is! A c kerületi sebesség ekkor a sugár és a szögsebesség szorzata lesz: c = r.ω = 2πν.r, ez a sugár tehát a hullámhosszal egyezik meg r = c/ 2πν. Mekkora lesz ekkor az impulzusmomentum? A forgástengelyt z irányúnak választva I_z = p.r = (h.ν/c).(c/2πν) = h/2π. A körforgás lehet jobb és balsodrású, ennek felel meg az impulzusmomentum z komponensének pozitív és negatív előjele. Emiatt a spin vetülete +1 és -1 lehet (spin alatt ℏ együtthatóját értjük: I =S.ℏ). Az egyezés teljes a kvantummechanikával és ami különösen fontos, hogy magyarázatot adtunk arra is, miért nem függ a foton impulzusmomentuma a frekvenciájától.

Miért terjed a fény egyenes irányban?

Ez az elképzelés arra is magyarázatot ad, hogy miért halad egyenes irányban a fény. A körforgáshoz tartozó impulzusmomentum a forgási tengely irányába mutat, ez pedig ugyanúgy fenntartja a mozgás egyenes irányát, ahogy azt a pörgő puskagolyó is megteszi.

Egy különös kvantummechanikai szabály

Van az impulzusmomentumnak a kvantummechanikában egy furcsa szabálya, amely szerint négyzetének sajátértéke nem S², hanem S(S+1) lesz, Ennek megfelelően foton esetén a sajátérték 2ℏ² értéket veszi fel. Ezt hogyan értelmezzük? A foton egyrészt halad a z irányban, másrészt a z irány körül forog, ez olyan  csavarmozgást hoz létre, amelyben a kerületen megtett út hossza egyezik a z irányú előrehaladással. Emiatt lesz az impulzusmomentumnak egy x és y irányú komponense is, amely azonban a körforgás miatt kiátlagolódik. (A kiátlagolódásnak felel mega kvantummechanikában a várható érték.) Fennmarad viszont az x és y komponens négyzetének összege, amely megduplázza a z komponens négyzetét, ezért a három komponens négyzetének összege kiadja a kvantummechanikai várható értéknek megfelelő 2 ℏ² értéket.

Az elektron impulzusmomentuma

A fentiekben a foton pályájához egyenes vonalat rendeltünk hozzá, amely mentén forog és halad, de milyen képet rendelhetünk az elektronhoz, amely szintén rendelkezik impulzusmomentummal, és így forgásról és véges sugárról kell beszélnünk. Az elektron spin definícióját a relativisztikus Dirac egyenletből lehet származtatni, mely szerint S = ½ és S² várható értéke ¾. Ez utóbbi az elektron izotrop jellegéből következik, mert az S_x, S_y és S_z komponensek négyzete egyaránt ¼, így az összeg kiadja az S(S+1) szabálynak is megfelelő ¾ értéket. De milyen forgás adhat fele akkora spint és hogyan lehet a forgás izotrop? Ha egyetlen tengely körül forgatunk, az kijelöl a térben egy irányt és egy kört. Az izotrop szimmetria azonban megköveteli, hogy a forgás gömbfelületen haladjon végig. Ez úgy lehetséges, ha két fénysebességű forgás kapcsolódik össze, az egyik létrehoz egy kört, de közben a forgás tengelye is körbe szalad, ahogy egy karikát is megforgathatunk átlója körül.

A foton esetén megadtuk a fénysebességű forgásnál a frekvencia és a sugár kapcsolatát. Akkor a 2rπ kerületet kellett befutni, az elektron esetén a 4r²π gömbfelületet kell bejárni, ami az impulzusmomentum számításban I_z = h/4π = ℏ/2 értékhez vezet, ezért kapunk S_z =½ értéket. A kettős forgással lehet magyarázni a részecske és antirészecske kettősséget, valamint a töltés eredetét is („Az elemi részecskék mozgásformái”, „Fénysebességű forgások és a relativitáselmélet”). Szintén értelmezni lehet az elektron mágneses momentumának eredetét („Az elektron anomális mágneses momentuma”).

A Pauli-féle kizárási elv

 A spin alapján lehet osztályozni a részecskéket, így a foton az S = 1 spin miatt bozon, az elektron viszont fermion, mert S = ½. A Pauli-féle kizárási elv szerint két elektron nem tartózkodhat ugyanabban az állapotban, viszont nincs ilyen tiltás bozonok esetén. Az elektron pozícióját a két forgástengely metszéspontja kijelöli, szemben a fotonnal, amit egyenes vonallal jellemezhetünk. A pontnak nincs szabadsági foka, ezért két elektron centruma nem eshet egybe csak akkor, ha spin vetületük előjele különbözik. Ez felel meg a Pauli-féle kizárási elvnek. Bozonoknak viszont van egy szabadsági fokuk: a vonal iránya. Emiatt nincs akadálya, hogy azonos állapotba kerüljenek.

Miért pontszerű az elektron a szóráskísérletekben?

Amikor a klasszikus mechanikában impulzusnyomatékról beszéltünk a kiterjedésen kívül a test merevségét is meg kellett követelni. Az elektronoknál más a helyzet, mert a fénysebességű forgás nullára zsugorítja a Lorentz kontrakció miatt a gömb felületét. Ez magyarázza, hogy ha az elektron pozitronnal bombázzuk a Bhabha kísérletekben, akkor az elektront nem lehet „eltalálni”, csak pontszerű töltésük határozza meg a szórás kísérletek eredményét. Sugaruk mégis van, mert a forgásra merőleges irányban nem következik be rövidülés, és ezt a sugarat „mérhetjük” is, amikor meghatározzuk az elektron impulzusmomentumát és mágneses momentumát. Tehát az elektron a tér egydimenziós alakzata és nem egy merev gömb. Ebből fakad, hogy az elektron és nagyobb tömegű „társai” (müon és tauon) olyan fizikai paraméterekkel (tömeg, frekvencia, impulzus- és mágneses momentum) rendelkeznek, amelyek egyetlen változóval leírhatók.

Folytonosság és kvantumosság a mikrovilágban

Amikor olyan kérdéseket vetünk fel, hogy milyen a sajátforgása az elektronnak, vagy a fotonnak, akkor olyan világba tévedünk, ahonnan nem érkezik számunkra közvetlen információ. A világ megértésében arra törekszünk, hogy a hétköznapi világból nyert fogalmainkat átvigyük abba a mikrovilágba, amit közvetlenül nem láthatunk. Műszereink segítenek ebben, így jutottunk el olyan fogalmakhoz mint az atom és molekula, majd ez is tovább bonthatónak bizonyult atommagra és  elektronokra, sőt ezen is továbbléptünk, amikor az atommagok alkatrészeiről beszélünk a nukleonokról és az ezeket felépítő kvarkokról.

Még ezen a skálám is túllépünk, amikor megkérdezzük, hogy leírhatjuk-e ezeket a parányokat a téridő mozgásaiként, amit én fénysebességű forgásoknak nevezek?  Ez a forgás már nem látható, mert számunkra a látás eszköze a foton, amely hírt ad az elektron, vagy egyéb elemi objektumok állapotának változásáról, de magát az állapotot nem mutatja meg nekünk. Jogos-e ezért egyáltalán arra törekedni, hogy mégis alkalmazni próbáljuk a hétköznapi világból nyert fogalmainkat, mint a forgás, a sugár és a nyomaték, van-e értelme megmagyarázni a kvantum eredetét? A fent vázolt elképzelés talán bizonyítja, hogy igenis van, mert eljuthatunk egy átfogóbb világképhez, amely a folytonosság fogalmára épül. Ez a folytonosság a forgások alapja, de amikor a megfigyelésekre kerül a sor, akkor nem láthatunk be a forgások részleteibe, csak a teljes forgások következményeit látjuk: a kvantumot, ami a fénysebességű forgások eredményeként jön létre. Tehát van egy mélyen fekvő folytonos világ, amely a tér forgásai révén számunkra kvantumokban mutatja meg magát. A kvantum tehát egy lépcsőfok a mikrovilágban, amely azonban ismét a folytonosságba megy át a makrovilágban, ahol ez a lépcsőfok olyan parányi, hogy nem vehető észre a hétköznapi tapasztalatok során.

A blog további írásait foglalja össze a linkekkel együtt a „Paradigmaváltás a fizikában” című bejegyzés.