Nyomozás a sötét anyag után
Mi a WIMP?
Univerzumunk egyensúlyát a gravitáció biztosítja, amelynek törvényét Einstein egyenlete írja le. Mekkora tömegmennyiségre és sűrűségre van szükség ahhoz, hogy magyarázzuk az Univerzum tágulását, a galaxisok mozgási sebességét, minek köszönhetjük, hogy az Univerzum képes évmilliárdokig fennmaradni a gyors széthullás, vagy összeroppanás veszélye nélkül? Ha az ehhez szükséges tömeget megbecsüljük és összevetjük csillagászati megfigyelésekkel, amelyben az összes csillag tömegét számba vesszük, kiderül, hogy a szükséges tömeg nagyobb része hiányzik. Hol lehet ez a hiányzó anyag? Ennek magyarázatára született meg az elképzelés, hogy a tömeget adó anyag nagy része rejtve van szemünk elöl, nem mutatható ki sem távcsövekkel,sem radarhullámokkal, sem egyéb eszközökkel. Ez a sötét anyag csak tömeggel rendelkezik, de nem lép kölcsönhatásba környezetével a gravitációs vonzáson kívül. Azokat a feltételezett részecskéket, amelyek a sötét anyagot alkotják, nevezik WIMP-nek: weakly interacting massive particles. De ilyen részecskékről nem tud a részecskefizika átfogó elmélete a Standard Modell sem. Van ugyan gyengén kölcsönható részecske, ez a neutrínó, amit avval szoktak jellemezni, ha egy neutrínó nyaláb fényévhosszúságú ólomtömbbe ütközik, akkor a részecskék fele kölcsönhatás nélkül fog áthaladni. A neutrínóval viszont az a baj, hogy az eredeti modell szerint tömeggel nem rendelkezik, ami abban nyilvánul meg, hogy a kísérletek szerint a fény sebességével halad. Újabban ugyan feltételezik, hogy valamilyen nagyon kis tömege azért lehet, mert létezik három egymásba átalakuló típusa, amit csak a tömeg létezése idézhet elő. Viszont a mozgás nagy sebessége miatt ez a tömeg csak nagyon kicsi lehet, amit úgy becsülnek meg, hogy a sebességmérés pontatlanságát a fénysebességtől való eltéréssel azonosítják. A WIMP magyarázatára azonban ez a lehetséges tömeg nagyon- nagyon kevés!
Kiindulópont a relativitáselmélet
A fizikai kalandozások során most arra teszek kísérletet, hogy megtaláljuk ezt a rejtélyes részecskét, a WIMP-et. Ennek során többször fogok hivatkozni korábbi bejegyzéseimre, amely segíteni fog a rejtély felderítésében. Induljunk hát neki a kalandtúrának, mint már annyiszor, a relativitáselmélet talajáról! A legutóbbi bejegyzésben „The origin of covariance in the special relativity” vetettem fel annak az okát, hogy miért négyzetesen adódik össze az energia két tagja, amelyik a mozgásból (ez a p.c tag) és a nyugalmi energiából (ez az m0c2) származik:
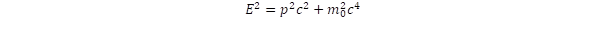
A magyarázat lényege, hogy a nyugalmi tömeg voltaképpen fénysebességű forgás eredménye, és a körbeforgó p0 impulzus hozzáadódik a külső mozgás impulzusához. A forgás szimmetriája miatt a saját impulzus átlaga (kvantummechanikában várható értéke) nulla, ezért a teljes impulzus négyzetének kifejezésében a két tag szorzata eltűnik és csak négyzetes összeg marad meg.
A Dirac egyenlet és a negatív energia dilemmája
A relativitáselmélet négyzetes törvényébe helyettesítve az energia és az impulzus operátorát jutunk el a kvantummechanikai mozgásegyenlethez, de ennek matematikai kezeléséhez az egyes tagok lineáris összegére van szükség, amit Dirac sikeresen oldott meg a négyzetgyökvonás négydimenziós mátrixokkal történő felbontásával. Ez a felbontás valójában négy csatolt differenciálegyenletet hozott létre. Ez a négy egyenlet két alternatívát fogalmaz meg, amiből az egyik a pozitív és negatív energia kettőssége, a másik a spin megjelenése, ami voltaképp az elektron sajátforgásának (perdületének) két lehetséges sodrásirányához – a jobb- és a balmenetűhez – kapcsolódik.
A negatív energiájú megoldások megjelenése azonban komoly elvi nehézséget okozott. A fizika egyik alaptétele, hogy a változások iránya mindig az alacsonyabb energia felé halad, így az elektronnak is át kellene ugrani a negatív energiák tartományába. A bajt viszont az okozza, hogy ennek a negatív tartománynak nincs alsó határa, le kellene hullani az elektronnak a mínusz végtelenbe. Ezt a problémát próbálta kiküszöbölni Dirac ötlete, mely szerint a végtelen számú negatív energiájú állapot már mind be van töltve és mivel a Pauli elv értelmében két elektron nem lehet azonos állapotban, így az elektron a pozitív tartományban marad. Előfordulhat azonban, hogy hiányzik egy elektron a negatív tartományból, azaz egy lyuk keletkezik. Az elképzelést látszólag igazolta, amikor Anderson felfedezte a pozitront, mert ennek tulajdonságai pontosan megfelelnek a lyukelektron hipotézisének, azaz a pozitront az elektron antirészecskéjének lehet tekinteni. Emiatt fogadták el Dirac abszurdnak tűnő feltevését a végtelenszámú negatív energiájú elektronról. Az elképzelés egyik hibája, hogy kiderült minden részecskének, így az egészszámú spinnel rendelkező bozonoknak is van antirészecskéje, viszont a bozonokra már nem érvényes a Pauli féle kizárási szabály! A lyukelmélet fontos tanulsága, hogy óvatosnak kell lennünk, amikor a fizikában valamit bizonyítottnak tekintünk. Ha az elmélet valamilyen jelenséget jól magyaráz az önmagában még nem bizonyíték, legfeljebb valószínűsítheti a hipotézis helyességét. Új kísérleti tény mindig előkerülhet, ami cáfolja elképzelésünk helyességét, ezért abszolút bizonyosságról sohasem beszélhetünk. Jogosan mondhatja az olvasó, hogy ez az én elgondolásaimra is igaz! Várom ezért az olyan kommenteket, ahol rámutatnak, hol sántítanak az általam ismertetett hipotézisek, milyen tényeknek mondanak ellent.
Mi a negatív energia eredete?
A negatív energiájú állapotok megjelenése a Dirac egyenletben a relativisztikus formula négyzetes jellegéből fakad. A negatív és pozitív számok négyzete megegyezik, ezért a gyökvonásnak mindig van pozitív és negatív megoldása is. Mivel maga a Dirac egyenlet a gyökvonás speciális megvalósítása, így elkerülhetetlenül fellép a negatív energia is. A kvantummechanikában az energia operátora az időszerinti deriválttal került definiálásra: ℏid/dt (Lásd: Út a kvantummechanika megértéséhez), így az energia negatív előjele az idő negatív irányával egyenértékű. A fizikai rendszer állapotát kétféle módon írhatjuk le vagy a jelen állapotból következtetünk a jövőbeli állapotra, vagy visszafele haladva a jelen állapotból írjuk le, hogy milyen lehetett a korábbi állapot. Relativisztikus egyenletünk nem választja szét azt a két lehetőséget, ezért egyidejűleg kapjuk meg mindkét leírási módot. Azt már nem kell bizonyítani, hogy nem lehet a múltba visszalépni, ezt az elvet a kvantummechanikának is tisztelni kell, ezért kizárhatjuk azt a lehetőséget, hogy a pozitív energiájú állapotból át lehet menni a negatív tartományba.
A spin és a Dirac egyenlet
A Dirac egyenlet másik nagy találmánya a spin. Ez is a relativisztikus egyenlet kvadratikus jellegéből fakad, mert a p2c2 tag is előállhat pozitív és negatív impulzusból és forgások esetén ez a két lehetséges sodrásirányban perdülő impulzusnak felel meg. A modern fizika a spinnel kapcsolatban nagyon óvatosan fogalmaz, mert valódi forgás helyett csak az elektron és más részecskék „intrinsic” (saját) tulajdonságának tekinti. Igazából fizikai kalandozásom eredete is az volt, hogy tisztázni akartam a spin eredetét, ami elvezetett a több bejegyzésben is tárgyalt fénysebességű forgások hipotéziséhez.
A részecskék, mint a tér királis szerkezetének szülöttei
Elővettem azt a kérdést is (lásd: Fénysebességű forgások és a relativitáselmélet I és II), hogy nem lehet-e a Standard Modell valamennyi részecskéjét – így az elektron és pozitron mellett a kvarkokat és a neutrínót is a relativisztikus energiaformula négyzetes alakjából levezetni. Így jutottam el az általános fermion egyenlethez, ami annyiban különbözik a Dirac egyenlettől, hogy bevezet egy harmadik kétdimenziós alternatívát a kiralitás fogalmán keresztül. A háromdimenziós térnek ugyanis két geometriai ábrázolása van (Lásd: A részecske fizika nyitott kérdései II), az egyikben a merőleges xyz tengelyek irányultsága a jobb kéz, a másikban a bal kéz szimmetriáját követi. Maga a relativisztikus egyenlet nem tesz különbséget a kétféle koordináta rendszer között, ezért alkalmas a kétféle kiralitás együttes tárgyalására. Ezt használtam ki a négydimenziós spinor algebra nyolcdimenziósra való bővítésével, amelyben az egyes részecskék a két királis szimmetria szuperponált állapotai. Tiszta királis állapot az elektron és a pozitron, a neutrínóban a két királis állapot egyenlő súllyal szerepel, míg a szuperpozíciós arányok eltérőek a kvark és antikvark két formája (up és down) között. (Valamennyi részecskének három „generációja" van, ahol a magasabb generációk a nyugalmi tömeg nagyságában különböznek, kvarkok esetén az up (u) kvark „rokonai" a charm (c) és a top (t), ugyanakkor a down (d) kvark esetén a strange (s) és a bottom (b). Az osztályozás alapja a töltések egyezése).
A kétdimenziós tömeg és elektromos töltés
A szuperpozíciós arányok megjelennek nemcsak a töltés, hanem a tömeg és az impulzus definíciójában is. A fizikai mennyiségek operátorát a kétdimenziós σz és σx Pauli mátrixok segítségével adhatjuk meg, ahol az előbbinek csak diagonális (+1 és -1), az utóbbinak csak nem diagonális (+1) eleme van. A részecske tényleges töltését és nyugalmi tömegét a kétdimemziós királis térben képzett diagonális elemek határozzák meg, a nem-diagonális elemek az impulzustól származó mozgási tömegnek felelnek meg. Az elektron és pozitron esetén a tömeg és töltés operátor diagonális, amit a kvantummechanika úgy fejez ki, hogy ezek „jó kvantumszámok”, ezeket mérni tudjuk; és ezek a mennyiségek a részecske olyan jellemző paraméterei, amelyek függetlenek az inercia rendszer választásától. Az impulzus viszont csak nem-diagonális elemekből épül fel, ezért az impulzus és a mozgási tömeg attól függ, hogyan választjuk meg a referencia rendszert. Neutrínó esetén mind a töltés, mind a nyugalmi tömeg mátrixa nulla diagonális elemekkel rendelkezik, ami azt jelenti, hogy ezeknek fizikai mennyiségeknek nincs mérhető értékük, az impulzus viszont diagonális, azaz független a referenciarendszer választásától és a részecske karakterisztikus paraméterének tekinthető. Ebből származtatható a neutrínók karakterisztikus mozgási tömege is: m = p/c. Kvarkok esetén egyaránt fellépnek diagonális és nem diagonális elemek, a töltés esetén a diagonális elemek adják meg a ±1/3 és ±2/3 értékeket. Kvarkok azonban nem detektálhatók, ezért sem a töltés, sem a tömeg nem mérhető kísérleti úton, csak elméleti értékek adhatók meg.
A kvarkok bezártsága a megfigyelhető részecskékben
A kvarkok megfigyelésére történő kísérletek azonban sikertelenek voltak, tört töltést egyetlen esetben sem találtak a nagyenergiájú mérésekben. Ezt magyarázzák a „bezártság” elvével, mely szerint az összetett részecskékből, így a kvark és antikvarkból álló mezonokból, illetve a három kvarkot tartalmazó barionokból nem lehet kiszabadítani a komponenseket. Emiatt a kvarkok tömegére csak indirekt módon lehet következtetni a mezonok és barionok tömegének szisztematikus analízisével, ez az un. renormálási eljárás. A d (down) és u (up) kvarkra kapott renormált tömegek (4,8 ill. 2,3 MeV) még együttesen is csak 1 százalékát teszik ki a neutron (udd) és a proton (uud) tömegének (939,565 ill. 938,272 MeV). A két nukleon tömegének különbsége (1,293 MeV) azonban elég közel van a két kvark tömegének különbségéhez. Ez arra mutat, hogy a nukleonok tömegét döntő mértékben a kvarkok közötti kölcsönhatási energia határozza meg és ez a kölcsönhatási tag jó közelítésben azonos a proton és a neutron esetében. A mezonok és barionok családjában egyaránt lehet találni olyan párokat, amelyek csak egy d illetve u kvarkban különböznek, ami lehetővé teszi a statisztikai analízist a kvarkok renormált tömegének meghatározására.
A tömegek relativisztikus összeadódása
Felvetődik azonban a kérdés, hogy mennyire indokolt a tömegek lineáris összegzése, nem lehetséges-e, hogy valójában a relativisztikus energiaképzés mintájára a tömegek és a kölcsönhatási tér energiájának négyzeteit kell összeadni? Ez indokolt lehet, azért is, mert a kvarkokból felépülő részecskék tömege nagyobb, mint amit a kvarkok együttesen kitesznek. Az atommagok esetén épp fordított a helyzet, ott a tömegdeficit jellemzi a mag stabilitását, amikor kisebb az eredő tömeg, mint a benne szereplő neutronok és protonok együttes tömege. Ezért lehet feltételezni, hogy a mezonok és barionok tömegtöbblete kinetikai jellegű energiából származik, ami viszont a relativitás elve szerint négyzetesen adódik össze a nyugalmi energiával.
Jelöljük Mu és Md-vel az u illetve d kvarkot tartalmazó részecskék tömegét, ahol is a négyzetes összegzési szabály szerint:
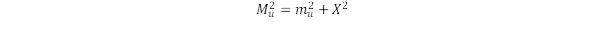
Itt mu az u kvark renormált tömege, míg X jelöli a többi kvark tömegjárulékát a kölcsönhatási energiával együtt. Hasonlóan írhatjuk fel az Md tömeget is, melyben feltételezzük, hogy az X járulék azonos és emiatt a két tömeg különbségére érvényes, hogy
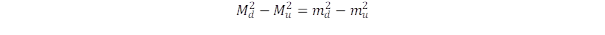
Rendezzük át az összefüggést a négyzetszámok különbségére vonatkozó algebrai szabály segítségével:
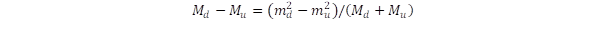
Az összefüggés alapján azt várjuk, hogy az egyes párokban a tömegek különbsége csökken, ha nagyobb a részecskék tömege. Természetesen jelentős szórást okozhat, hogy az X érték nem pontosan egyenlő a pár két tagjában. A mezonokra és barionokra vonatkozó mérési eredmények közül kiválasztjuk a feltételnek megfelelő párokat, beleértve olyan adatokat is, amikor a részecskékben két u illetve két d szerepel, de ekkor az Md – Mu különbséget felezzük. Összesen 4 mezon és 12 barion esetén találtunk megfelelő párt a szakirodalmi táblázatokban, a rájuk vonatkozó számítások eredményét összegzi az ábra:
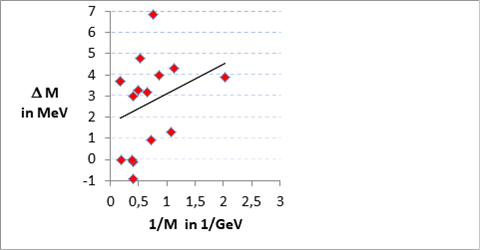
A részecskepárok tömegkülönbsége a részecske tömegek reciprokának függvényében
Látható, hogy bár jelentős szórással, de a trend a várakozásnak megfelelően csökken a nagy tömegű részecskék esetében.
Felhasználva ugyanezeket az adatokat meghatározhatjuk a d és u kvark négyzetes tömegének a különbségét is, ami átlagban 11 280-nek adódik, és ennek megfelelően a d kvark tömege legalább 106 MeV. Ha feltételezzük, hogy a d kvark kétszer nehezebb az u kvarknál, akkor 122 illetve 61 MeV értékeket kapunk a tömegekre. Ezzel szemben lineáris összegzés esetén md – mu = Md – Mu , ami md – mu = 2,6MeV átlagértékre vezet. Tehát a négyzetes szabály alapján becsült tömeg több mint egy nagyságrenddel haladja meg a Standard Modellben számolt értéket. Figyelemre méltó, hogy a legkönnyebb és legstabilabb π0 és π+ mezonok esetén, amelyek az u kvark és d kvark és antikvark kombinációjából épülnek fel, a négyzetes összegzési szabály alapján becsült tömeg 136,4 MeV lesz, ami épp a kísérletileg talált 135,0 és 139,6 MeV értékek közé esik. Ugyanakkor az atommagokat alkotó uud és udd szerkezetű protonoknál és neutronoknál a négyzetes szabályból számolható tömegek 149,4 és 183 MeV jóval kisebbek, mint a tényleges 938,272 és 939,565 MeV értékek, ami arra mutat, hogy a kölcsönhatási tér energiája a három kvarkból felépülő részecskékben sokkal nagyobb, mint a kvark és antikvark kombinációjú mezonokban.
Lehet, hogy mégis a neutrínó a tettes?
A sötét anyag titkához azonban nem a kvarkok tömege adja meg a kulcsot, mert amikor létrehozzák a nukleonokat és egyéb részecskéket, akkor mindig egész töltés és evvel együtt diagonális tömeg alakul ki. Nem vonatkozik ez a neutrínókra, az univerzum magányos vándoraira, ezeket a részecskéket csak a fekete lyukak foghatják be az erős gravitációs hatáson keresztül. De mekkora a tömegük, hiszen a mérések szerint vagy nulla, vagy nagyon csekély. Itt lép be a képbe, hogy ugyan a neutrínónak nincs diagonális tömege, de van diagonális impulzusa, aminek megfeleltethető az m = p/c = E/c2 mozgási tömeg, márpedig a gravitáció szempontjából ez a mérvadó. A neutrínó sajátimpulzusának létezése egyúttal magyarázatot ad arra is, hogyan értelmezzük a három különböző neutrínó egymásba való átalakulását, a neutrínó oszcillációt.. Friss hír: A neutrínó oszcilláció felfedezéséért 2015-ben a fizikai Nobel díjat Kadzsita Takaaki és Arthur B. McDonaldnak ítélték oda. Arra viszont nincs információ, hogy mekkora is lehet a saját impulzushoz tartozó mozgási tömeg, de valószínűsítheti a nagyságrendet a neutrínó eredete, amely a bétabomlásból származik (Lásd: Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása I és II). A neutron bomlásakor képződik az egyik d kvarkból egy u kvark és egy W- bozon. Ez a bozon – amelynek óriási tömege van: 80,385 GeV – bomlik fel egy neutrínóra és egy elektronra. De hova lesz ez a hatalmas tömeg, ez a hatalmas energia, vajon nyomtalanul eltűnik? Vagy inkább átadásra kerül a neutrínónak, amelyhez m = E/c2 mozgási tömeg rendelhető hozzá. Tovább erősíti ezt a feltételezést a neutrínó oszcilláció jelensége, ez csak a semleges Z bozonok segítségével történhet, hiszen a neutrínóknak a gravitáción kívül ez az egyetlen kölcsönhatási mechanizmusa. A Z bozon tömege még a W bozonnál is nagyobb: 91,188 GeV. Tehát a neutrínók „rejtett” tömege is ebbe a nagyságrendbe eshet, azaz a neutrínó nem a részecskevilág törpéje (becslések szerint még az elektronnál is milliószor könnyebb), hanem az óriása, ami még a neutronnál is százszor nagyobb lehet! Ha igaz ez a feltételezés, akkor nem kell tovább keresni a sötét anyagot. Ott volt már régen a szemünk előtt, csak nem vettük észre, mert alábecsültük a neutrínók fontos szerepét az Univerzum gravitációs egyensúlyának fenntartásában. A csillagok a termonukleáris reakciókban ontják magukból a rejtélyes neutrínók áradatát, (csak a Nap belsejében másodpercenként 3,8.1034 neutrínó keletkezik), amely teljes tömegében meghaladhatja az általunk látható galaxisok által hordozott tömeget.
Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.