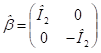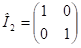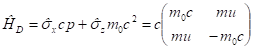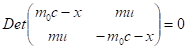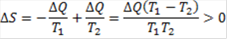FOLYTATÁS
A részecskefizika nyitott kérdései II
Az erős gravitáció és a tér fénysebességű forgásai
Rockenbauer Antal
Az elemi részecskékre vonatkozó ismereteinket a Standard Modell foglalja össze. Legfontosabb megállapításai, törvényei elfogadásra kerültek a fizikusok döntő többsége által. Anélkül, hogy vitatnám ezeknek a törvényeknek a helyességét, fölvetem azokat a kérdéseket, amelyeket ez a modell vagy nem oldott meg, vagy amivel egyáltalán nem is foglalkozik, majd bemutatok egy olyan elképzelést, amely számos felvetett kérdésre egységes és ellentmondásmentes választ tud adni. Mindjárt a bevezetőben ismertetem ennek lényegét, ami nagyon röviden összefoglalható: minden elemi részecske létezése a fénysebességű forgáson alapul. Gondolataim alapjául két fizikai törvény szolgál: az egyik a speciális, a másik az általános relativitáselmélet. Mivel az a célom, hogy a leírtak érthetőek legyenek azok számára is, akik nem otthonosak a relativitáselmélet világában néhány egyszerű hasonlattal bemutatom a két elmélet számunkra fontos tételét. Azok számára, akik a pontos matematikai kifejtésre kíváncsiak hívom fel a figyelmet a témában megjelent angol nyelvű publikációmra.[1]
1. Rockenbauer: A screw model for quantum electrodynamics: From gravitation to quanta Indian J. Physics, 89, 389-396 (2015) ,
MI a kiralitás?
Mielőtt a fermionok forgási szerkezetét tárgyalnánk, tisztázzuk a kiralitás fogalmát. A különböző szimmetriaműveletek közül a háromdimenziós térben értelmezett forgatás fizikailag is megvalósítható művelet. Ez azt jelenti, hogy a koordinátatengelyek irányát tetszés szerint választhatjuk ki. Válasszuk ki először az x és y tengelyt egymásra merőlegesen. Ha a papír síkjában maradunk, akkor az x és y tengely viszonya kétféle lehet, szokás szerint a pozitív 90 fokos forgatás, ami az óramutató járásával fordított sodrásirányt jelent, viszi át az x tengelyt azy tengely irányába. Definiálhatjuk azonban úgy is a koordinátarendszert, hogy az y tengely iránya mínusz 90 fokkal tér el az x tengelytől. Ha a síkból nem lépünk ki, akkor semmilyen forgatással nem tudjuk a két rendszert egymásba átvinni. Tükrözzük azonban a két tengely szögfelezőjére a koordinátákat, ekkor a két sodrásirányú rendszer átmegy egymásba. A tükrözést akkor tekintjük fizikailag is megvalósítható műveletnek, ha van olyan forgatás, amivel azonos eredményre vezet. Forgassuk el az xy koordináta tengelyeket a szögfelező körül 180 fokkal, ekkor ugyanazt kapjuk, mint az előző tükrözéssel. Ez a művelet azonban már a harmadik térdimenzióban történik, hiszen ez a forgatás már kilép a síkból. Ha tehát egy kétdimenziós világra korlátozzuk magunkat, akkor a tükrözés nem végrehajtható fizikai művelet, de ha egy háromdimenziós világból szemléljük a sík két tengelyének tükrözését, akkor a művelet fizikailag végrehajtható lesz. Az elmondottak szerint a kétdimenziós világban két egymásba át nem vihető xy koordinátarendszer definiálható, az egyik az óramutató járásával egyező, a másik ellentétes sodrásirányú x és y tengelyeket határoz meg, ha azonban megengedjük a kilépést a hármadik dimenzióba, akkor ezek a koordinátarendszerek már azonosak lesznek.
A háromdimenziós xyz koordinátarendszer felrajzolásakor az előzőek szerint az általánosság sérelme nélkül definiálhatjuk úgy az x és y tengelyeket, hogy a pozitív sodrásiránynak feleljen meg az irányítás. A harmadik tengely, amit z-vel jelölünk, azonban kétféle irányban definiálható: mutathat az xy síkból felfelé, ez a szokásos választás, de mutathat lefelé is. Az előzőt nevezhetjük jobbsodrásúnak, az utóbbit balsodrásúnak. Ennek szemléltetésére nyissuk ki jobb kezünk tenyerét, tartsuk vízszintesen és tenyerünk nézzen felfelé. Jelölje az x irányt a hüvelyk új, az y tengelyt a mutató új és mutasson a z irány felfelé. Tegyük most ugyanezt a balkezünkkel, de ezúttal a tenyerünk nézzen lefelé, hogy a hüvelyk és mutató új által definiált xés y tengelyek sodrásiránya megfelelő legyen. Ekkor azonban a z irány lefelé fog mutatni. Hiába forgatjuk azonban két tenyerünket, nem tudjuk úgy egymásra rakni, hogy az újaink fedjék egymást, azaz a háromdimenziós világunkban van két egyenértékű, de különböző koordinátarendszerünk. Megtehetjük persze, hogy két tenyerünket egymás felé fordítjuk, ekkor a két kéz egymás tükörképe lesz, de ez a tükrözési művelet a háromdimenziós térben nem felel meg semmilyen forgatásnak.
Fölmerül azonban a kérdés – egyébként pont az ilyen kérdések lendítik tovább a matematikát – vajon a négydimenziós téridőben átvihető-e egymásba a jobb és balsodrású rendszer? A válasz igen, de azért itt egy kicsit vigyázni kell! A relativitáselmélet összekapcsolja a tér és az idő koordinátáit, azonban a szimmetria nem teljes, mert az téridőben definiált távolság hosszában az idő koordinátától származó tag előjele negatív7. Van egy másik különbség is: az idő kerekeit nem lehet visszafelé forgatni. Ennek jelentőségét úgy érthetjük meg, ha meggondoljuk, mi történik, amikor az xy síkban levő tengely körül egy 180 fokos forgatást hajtunk végre az x és y tengelyek szögfelezőjére történő tükrözés helyett: ekkor a z tengely iránya megfordul, azaz a forgatás a z tengely irányát tükrözi. Úgy is általánosíthatjuk ezt a megállapítást, hogy egy alacsonyabb dimenziójú térben végrehajtott tükrözés olyan magasabb dimenziójú térben végrehajtott forgatásnak felel meg, amikor az új dimenziót megadó koordinátatengely iránya megfordul. Ha most a jobbsodrású xyz koordinátarendszert forgatjuk át a balsodrásúba, akkor olyan téridő forgást kell alkalmazni, amikor az idő iránya előjelet vált. Mivel ez nem lehetséges, így a relativitáselméletben definiált téridő bár négy dimenzióval rendelkezik, mégsem találunk olyan végrehajtható forgatást, ami a kétféle xyz rendszert egymásba átviszi. Matematikailag létezik ugyan ilyen forgatási művelet, de ez a tapasztalati világban nem hajtható végre.
Persze lehet tovább kérdezni: igaz, hogy mindennapi tapasztalataink világában az idő nem fordítható meg, de ez nem szükségszerűen teljesül az elemi részecskék birodalmában. Itt válaszul hivatkozhatunk a korrespondencia elvre: ha nagyszámú részecske tulajdonságait vizsgáljuk, akkor a kvantummechanikai törvények folytonosan átmennek a klasszikus fizika megállapításaiba. Tehát nagyszámú olyan folyamat együttese, amelyben megfordítható lenne az idő, már elvezetne olyan megfigyelésekre, ahol makroszkopikus méretekben tudnánk az idő irányát megfordítani. Képzeljük el, hogy mégis visszatérhetnénk a múltba és megváltoztatnánk valamit, ami megakadályozná, hogy megszülessünk. De ha meg sem születtünk, akkor hogy tehetnénk meg a múltba való kirándulást? Az idő irányának megfordítása ezért az oksági elvre alapuló egész logikai világlátásunknak mondana ellent. Az írás egyik célja, hogy hidat találjunk a modern fizika fogalomrendszere és a józanész között. A legfontosabb ilyen híd a korrespondenciaelv a makro- és mikrovilág törvényei között. Ezt felhasználhatjuk, hogy áthozzunk fogalmakat a modern fizikából a józanész világába, de a híd fordítva is járható: időnként a józanész alapján tehetünk mérlegre divatos elméleteket. Így például a józanészre támaszkodva ítélhetjük meg azokat a szofisztikált fizikai elméleteket, amelyek megengedik az idő irányának megfordítását.
A fentiek miatt léteznek a háromdimenziós térben olyan objektumok, amelyek egymás tükörképei, de forgatással nem lehet egymásba transzformálni ezeket, ehhez kapcsolódik a kiralitás fogalma. Ha egy molekulában a szénatomhoz három másik atom kapcsolódik, például egy oxigén kettős kötéssel, egy hidrogén és egy klór, akkor síkban ábrázolva a három atom sorrendje lehet például O, H, Cl, de lehet O, Cl, H is. Azt hogy melyik atommal kezdjük a sort tetszés szerint választható, de amíg a síkban maradó kétdimenziós forgásokra szorítkozunk a két sorrend nem vihető át egymásba. Elforgathatjuk azonban a molekulát a CO tengely körül 180 fokkal – azaz kilépünk a síkból a forgatással – evvel már a két sorrendet egymásba tudjuk transzformálni. Emiatt azt mondjuk, hogy a két molekulaszerkezet azonos. Más a helyzet, ha négy különböző atom, vagy atomcsoport kapcsolódik a szénatomhoz. Legyen például, OH, H, Cl és F a négy szénhez kötődő csoport, illetve atom. Vegyünk két különböző sorrendet: OH, H, Cl, F illetve OH, H, F, Cl. Most ha egy forgatással a fluor és klór helyet cserél, akkor egyúttal megváltozik az OH és H sorrendje is, ezért nem lehet a két molekulát egymásba forgatni. Ebből a szempontból közömbös, hogy a négy kapcsolódó atom egy síkban fekszik, vagy egy tetraéder csúcsaiban helyezkedik el. Ilyenkor beszélünk kiralitás párról, amelyben azonos atomok kapcsolódnak össze, de a geometriai szimmetria mégis különbözik [2]. Ha két molekula kapcsolódási struktúrája azonos, és létezik a fenti értelemben definiált aszimmetrikus szénatom, akkor optikai izomerekről, vagy enantiomerekről beszélünk. Az optikai izomerek eltérő fénytani tulajdonságokkal rendelkeznek: amikor fotont nyelnek el, vagy bocsátanak ki, akkor a két esetben eltér a polarizáció sodrásiránya.
Kiralitás párok alakulhatnak ki, ha valamilyen tengelyre csavarunk fel egy szálat, itt is megkülönböztethetjük a jobb és balsodrású esetet, amit a haladási irányra vonatkoztatunk. A csavaroknál is ismerünk jobb és balmenetűeket, ahol a haladási irányt a csavar feje illetve hegye különbözteti meg. A biológiában a legismertebb példa a DNS molekula két összefonódó spirális párja, de itt mindig a jobbmenetű fordul elő szervezetünkben. Érdekes módon a természet a biológiai folyamatokban előnybe részesíti az L- típusú aminosavakat (balra forgató), és a D-típusú cukrokat (jobbra forgató).
A természet általában szereti a szimmetriát, de bizonyos esetekben mégis kénytelen a két lehetőség közül választani. Erre is találunk példát az anyag és antianyag kettőségével kapcsolatban. A fotonok esetén is létezik ez a kettőség: az elektromágneses tér körforgása a haladási irány körül lehet jobbsodrású és balsodrású is, az egyik esetben az impulzusmomentum iránya előre, a másikban hátrafelé mutat. Ez a jelenség a polarizált fény elnyelésekor és kibocsátásakor játszik szerepet, amit a kibocsátó vagy elnyelő molekula kiralitása határoz meg.
[2] Ez nem azonos a kémiai nevezéktan izomerjeivel, ahol az atomok bruttó összetétele megegyezik, de egymáshoz való kötésszerkezetük eltér.
Fermionok mint kettős forgású részecskék: a gömbforgás
Az egyedi fermionok gömbszimmetrikus részecskék, ez azt jelenti, hogy valamennyi kölcsönhatás független az iránytól. Szemben a fotonnal, ahol a saját mozgások terében a forgástengely kitűz egy belső irányt, a fermionok olyan sajátmozgást végeznek, ahol minden irány egyenrangú. Ez úgy jöhet létre, ha maga a forgástengely is forog, tehát két forgás kapcsolódik össze. Úgy is felfoghatjuk a kettősforgást, hogy az első forgás egy kört ír le, a másik pedig megforgatja a kört tengelye körül és ezáltal gömbfelszínt hoz létre. A részecske elképzelésénél abból is kiindulhatunk, hogy a fermionok – a neutrínó kivételével [3] – rendelkeznek nyugalmi tömeggel és elektromos töltéssel, de ezek a fizikai mennyiségek a térben lokalizáltan jelennek meg. Egytengelyű forgásnál nincs lokalizáció, mert a foton bárhol lehet a forgástengely mentén, szükség van ezért valamilyen pontkijelölő mechanizmusra, aminek megfelel a kéttengelyű forgás, ahol metszi egymást a két forgástengely. Hasonló a helyzet – amint látni fogjuk a gyenge kölcsönhatás közvetítő bozonoknál is – ott a forgástengelyre merőleges transzláció egyenese jelöli ki a tér egy meghatározott pontját.
A kéttengelyű forgások lehetnek jobb- és balsodrásúak, azaz kiralitás tulajdonsággal rendelkeznek. Emiatt van minden fermionnak egy antifermion párja. Ez kézenfekvő magyarázatot ad arra, hogy miért létezik minden részecskének antianyag párja, és nincs szükség arra, hogy végtelenszámú betöltött állapotból hiányzó lyuk formájában értelmezzük az antirészecskéket [4].
A fotonokat, mint egytengelyű fénysebességű forgásokat értelmezve jutottunk arra a következtetésre, hogy bármekkora is legyen a forgási frekvencia a foton impulzusmomentuma azonos lesz, mert amilyen mértékben növekszik a szögsebesség, olyan mértékben rövidül a sugár. Hasonló szabály érvényes a kettős forgást végző fermionokra is. Viszont ekkor a „második” forgás megfelezi az impulzusmomentumot. Ez abból következik, hogy amíg a fotonoknál a forgástengelytől való r távolság határozta meg a nyomatékot, a fermionoknál az r sugarú kört forgatjuk meg főtengelye körül és emiatt a nyomaték feleződik [3]. A kéttengelyű forgás ily módon nagyon egyszerű geometriai magyarázatot ad arra, hogy miért éppen fele akkora a fermionok spinje, mint a fotonoké és az is érthetővé válik, hogy a nagyságrendekben különböző tömegű elemi objektumok miért rendelkeznek azonos impulzusmomentummal, azaz spinnel [4].
A kettős forgás miatt az extrém módon torzult tér centripetális erejének két különböző forgás centrifugális erejét kell kiegyenlíteni:
ℏc/r2 = 2mω2r
Ez az erőtörvény viszont ekvivalens a potenciális energia és a nyugalmi energia egymást kiegyenlítő hatásával [5]:
ℏc/r = mω2r2 = m.c2
Az innen származtatott sugár r = ℏ/mc megegyezik avval a Compton-hullámhosszal, ami az elektronoknál és más elemi objektumoknál megfigyelt interferencia jelenségben játszik szerepet. Ez összhangban van a részecskék kettős természetével, amelyek egyaránt rendelkeznek hullám és korpuszkuláris tulajdonságokkal.
További kérdés, hogy miért nincs elektromos töltése a fotonnak és miért van az elektronnak és a pozitronnak? A magyarázatot a forgó rendszerben fellépő második számú tehetetlenségi erő adja meg. A centrifugális erőtől már szó volt, amely a sugárirányban kifelé hat és nagysága arányos a keringő test impulzusával és a forgási frekvenciával. Ha azonban a körforgást végző rendszeren belül egy test mozog, akkor ennek pályájára csavaró erő hat, amit Coriolis-erőnek [6] hívunk. Ez az erő szintén arányos az impulzussal és a forgási frekvenciával, de iránya nem kifelé mutat, hanem merőleges egyfelől a forgás tengelyére, másfelől és a test haladási irányára. Az említett három irány alkothat jobb és balsodrású rendszert is. Példaként gondoljunk a Földön kialakuló tenger- és légáramlatokra, amelyek forgásiránya ellentétes az északi és a déli féltekén. Ennek oka, hogy az áramlatok a hideg sarkok felöl a meleg egyenlítő irányában indulnak meg és így a Föld északtól délre mutató forgástengelyéhez viszonyítva ellentétes lesz az áramlatok iránya. Ugyanilyen Coriolis-hatás lép fel a kettős forgás miatt is, ahol a két forgás egymáshoz képest jobb- vagy balsodrású kiralitással rendelkezik, az egyiket rendelhetjük az elektronhoz, a másikat a pozitronhoz. A csavaró hatás egytengelyű forgásokat indít meg, ez nem más, mint a foton modellünkben. A kvantumelektrodinamika úgy értelmezi a töltött elemi részecskék közötti vonzást és taszítást, hogy például az elektron és a proton virtuális fotonokat bocsát ki, ahol a fotonok polarizációját a töltés előjele határozza meg. A különböző polarizációjú virtuális fotonok összegződő, vagy egymást kioltó hatása hozza létre a taszítást, vagy vonzást a töltött objektumok között. Itt a virtualitás azt jelenti, hogy ezek a fotonok nem „láthatók”, szerepük csupán az erőhatás közvetítése.
A kettős forgás Coriolis-ereje megegyezik nagyságát nézve a centrifugális erővel, azaz ℏc/r2, mert a két forgás tengelye merőleges egymásra. A fotonok viszont nem rendelkeznek töltéssel, mert a haladási irányuk párhuzamos a forgás tengelyével és így a Coriolis-erő nulla [6]. A fotonok csavarforgása „rákapcsolódik” a töltött objektumok csavaró erejére, ezért alkalmasak két töltött objektum közötti kölcsönhatás közvetítésére. A fermionok és fotonok – más szóval a kettősforgások és az egytengelyű csavarforgások – közötti csatolás állandója határozza meg, hogy milyen erős lesz két, egymástól R távolságban lévő elemi töltés között a kölcsönhatási erő, azaz a Coulomb-erő
FCoulomb = e2/R2 = aℏ.c/R2
Itt az a = 1/137 csatolási tényező a nevezetes Sommerfeld-féle finomszerkezeti állandó. Mivel a Coriolis-erő nagysága nem függ a részecskék forgási frekvenciájától, és ezáltal tömegétől, ezért a saját impulzusmomentumhoz (spinhez) hasonlóan valamennyi elemi fermion töltése azonos, csak előjelük különbözhet a kiralitástól függően [7]. Evvel egy újabb, a Standard Modell által nyitva hagyott kérdésre adtunk választ.
Létezik a fermionok és fotonok között két átalakulási folyamat is. Ha egy elektron és pozitron ütközik, akkor fotonokra sugároznak szét. Ezt a jelenséget a Dirac-féle lyukelmélet szemléletesen magyarázza: az elektron beleesik a negatív energiájú elektrontengerből hiányzó lyukba. Legalább ennyire szemléletesen magyarázhatjuk az annihilációs mechanizmust a kettősforgásokkal is. Az elektron és pozitron másodlagos forgása ellentétes irányú, ezért ütközéskor megsemmisítik egymást. Tehát csak az egyik forgás marad meg, ami a vázolt modell szerint épp a foton! Ennek a folyamatnak a fordítottja a párképződés, amikor egy nagyenergiájú foton ütközéskor elektron-pozitron pár jön létre. Ekkor a foton c sebességű transzlációs mozgása hasad fel két ellentett értelmű másodlagos forgásra, vagyis két ellentétes kiralitású részecske keletkezik.
Felmerül a kérdés, hogy miért éppen 1/137 a Coulomb-erőt meghatározó csatolási tényező? Erre nincs jelenleg valódi magyarázat. Az állandó úgy tekinthető mint két különböző mozgásforma közötti csatolási együttható, ami a téridő egyelőre ismeretlen struktúrájából fakad. Hasonlóan nincs magyarázat arra sem, hogy az elektronhoz hasonló fermionok, mint a müonok és tauonok miért éppen 207-szer, illetve 3479-szer nagyobb tömeggel, azaz forgási frekvenciával rendelkeznek. Az is kérdés, hogy egyáltalán miért csak jól definiált tömegű fermionok keletkeznek, hiszen a fotonok esetén nincs korlátozva a frekvencia. A kérdések megválaszolásához szükség lenne a téridő szerkezetét mélyebben feltáró elméletre. Jelenleg csak feltételezhetjük, hogy a részecskeképződés a két forgás rezonanciáját igényli. Valamennyi mérésben, ahol megkísérelték a neutrínók terjedési sebességét meghatározni, a fénysebességet kapták a mérési pontosság határán belül. Ez azt valószínűsíti, hogy a neutron nyugalmi tömege nulla, hiszen csak ekkor mozoghat c sebességgel. Ennek ellentmondani látszik, hogy a neutrínónak három generációja létezik, az elektron-, a müon és a tauon típusú részecske es ezek egymásba alakulnak. Ezt nevezi a szakirodalom neutrínó oszcillációnak. De ha létezik három típus, akkor ezeket a nyugalmi tömegük különböztetheti meg. Ez a kérdés is a modern fizika egyik megoldatlan rejtélye..
[3] A nyomatékszámításnál a tengelytől való tömegpontok távolságainak négyzetét kell összegezni. Az r sugarú és m tömegű karika tehetetlenségi nyomatéka m.r2, ha a körre merőleges szimmetriatengely körül forgatjuk meg. Ha viszont a síkban fekvő főtengely körül forgatunk, akkor a tehetetlenségi nyomaték feleződik. Emiatt, ha a forgás sebessége azonos, akkor az utóbbi esetben a karika impulzusmomentuma pontosan a fele lesz az előbbinek.
[4] Az impulzusmomentum együtthatója a spin irányfüggő, azaz vektor mennyiség. Amikor S = ½, 1 … spinről beszélünk, ez alatt a vektor hosszát értjük. A spinnek azonban a hosszán kívül csak egyetlen komponensét lehet meghatározni, ami konvenciószerűen a z irányú vetület, ennek értéke M = S, S-1, … -S lehet, például S = ½ esetben M = ½ és -½, S = 1 esetben M = 1, 0 és -1. Kivételt jelent a szabály alól a foton, illetve az S = 1 kölcsönhatást közvetítő bozonok esete, mert ott M csak két értéket (+1 és -1) vehet fel. Ennek oka, hogy az egytengelyű forgásnak csak kétféle forgási (polarizációs) iránya lehet, hasonlóan az S = ½ fermionokhoz. Az utóbbi esetben a polarizációs irány a két forgástengelyre egyaránt merőleges harmadik irány. Mágneses térben ez az irány határozza meg a tengelyt, ami körül a fermion mágneses momentuma Larmor-precessziót végez. A precesszió sodrásirányát a részecske kiralitása határozza meg, ami eltérő lesz elektronok és pozitronok esetén.
[5] A ℏc/r = mω2r2 összefüggést az r változó szerint deriválva kapjuk az erőkre vonatkozó összefüggést
[6] A forgó rendszerben mozgást végző testre ható Coriolis-erő 2pxω=2m.uxω, ahol u, p és ω vektorok, melyek vektorszorzatát képezzük A vektorszorzat iránya merőleges a két komponensre, a tényezők sorrendjének felcserélése megfordítja az előjelet. A Coriolis-erő akkor a legnagyobb, amikor a forgási tengely merőleges a haladási irányra, viszont nulla lesz, amikor a két irány párhuzamos.
[7] Ez alól kivételt képeznek a kísérletileg megfigyelhetetlen, de a barionok és mezonok szerkezetét jól magyarázó kvarkok, melyek egyharmad és kétharmad töltéssel rendelkeznek. Ezt a későbbiekben kevert kiralitású részecskeként értelmezzük.
A negatív energia állapotok és az idő iránya
Diracnak azért volt szüksége, hogy feltételezze a végtelen számú negatív energiaállapot betöltöttségét, hogy magyarázza miért nem hullik le ebbe az állapotba az elektron, vagy más szavakkal miért lehet stabilis pozitív energiájú pályán, hiszen a kvantumfizika törvényei szerint az elektronnak el kell foglalnia a legkisebb energiájú pályákat. Ebből a koncepcióból következett a lyukelmélet, amit látszólag bizonyított is a pozitív töltésű pozitron megfigyelése. Amint már kifejtettük korábban, a pozitron tulajdonságait jól lehet értelmezni a kettősforgások kiralitásával, de még nem adtunk arra magyarázatot, hogy mi a helyzet az elektron negatív energiájú és negatív tömegű megoldásaival.
A Dirac-egyenlet alapja a relativitáselmélet energiára definíciója, amely négyzetes összefüggést ad meg a különböző tagok között. Ez szükségessé teszi a gyökvonás alkalmazását, így viszont a művelet kétértékűsége miatt egyaránt lesznek pozitív és negatív megoldások. Az energiát a kvantummechanikában olyan operátor határozza meg, amelyik az időszerinti változást írja le (parciális derivált). Ebből viszont az következik, hogy az idő irányának megfordítása az energia előjelét változtatja meg. Az időbeli folyamatok leírásánál két utat követhetünk: elindulhatunk a jelenből a jövő felé, de meg is fordíthatjuk a dolgot, amikor a múlt irányában vizsgáljuk a jelenséget. Relativisztikus egyenleteink nem különböztetik meg ezt a két utat, ami kifejeződik az egyenlet kvadratikus jellegében. Ami megtehető a jelenség matematikai leírásában nem tehető meg ténylegesen: a múltba nem lehet visszatérni. Viszont a negatív energiájú megoldás épp azt jelenti, hogy az időben visszafelé haladunk. Ha az elektron a pozitív energiájú állapotból átmenne a negatív tartományba, ahol még a tömeg is negatív, akkor megvalósítaná a múltba való visszatérést. Ez lehetetlen, tehát létezik egy kiválasztási szabály, amely megtiltja az ilyen típusú kvantumátmeneteket. Emiatt a már eleve betöltött negatív energiájú állapotok feltételezése nélkül az elektron ott maradhat a legkisebb pozitív energiájú állapotban.
A gyenge kölcsönhatás mint spirálmozgás
A különböző típusú fermionok átalakítását előidéző erőt nevezzük gyenge kölcsönhatásnak. Szemben az elektromágneses kölcsönhatással, amely csak a fermionok állapotát változtatja meg, ez az erő megváltoztatja a fermionok nyugalmi tömegét és elektromos töltését is. A mezőelmélet az átalakulásokat szintén S = 1 spinű bozonokkal értelmezi, de ezeknek van tömegük, sőt töltésük is lehet, így a W- részecske töltése az elektronéval, a W+ bozoné a pozitronéval egyezik meg, a Z bozon viszont töltés semleges. A gyenge kölcsönhatási bozonok tömege rendkívül nagy, közel 200 000-szer haladja meg az elektronét [8]. A legismertebb átalakulási folyamat a rádióaktivitásból ismert béta-bomlás, amikor a neutron protonná alakul át egy elektron és egy neutrínó [9] kibocsátása mellett.
Az átalakulás két lépcsőben történik, először a neutron protonná alakul át [9] egy W- bozon kilépésével, majd a második lépcsőben válik szét a bozon egy elektronra és egy neutrínóra. Az a meglepő a folyamatban, hogy a neutron egy nálánál százszor nehezebb bozont bocsát ki. Higgsezt a tér spontán szimmetriatörésével magyarázta, amit – összhangban evvel az elképzeléssel – a tér fénysebességű forgás által létrehozott torzulásával értelmezünk. A forgás a W bozon esetén is egytengelyű, mert a spin S = 1. De miért van ennek a bozonnak tömege és töltése is, amikor a szintén egytengelyű forgásként értelmezett fotonnak egyik sincs? A választ a forgáshoz kapcsolódó transzláció iránya adja meg. A gyenge kölcsönhatású bozonok esetén a transzláció iránya merőleges a forgás tengelyére. Ekkor fellép a Coriolis-féle csavaró erő, amely pontosan megegyezik az elektronéval, a töltés előjelét pedig a kiralitás határozza meg. A merőleges irányú transzláció metszi a forgástengelyt, ami által kijelöl a térben egy pozíciót, és így létrejöhet a térben lokalizált tömeg is. A tömeg-energia ekvivalencia miatt ugyanis mindig van tömeg, ez vonatkozik a fotonra is, de a fotonnál ezt a tömeget nem tudjuk hova tenni, ekkor csak mozgási tömegről beszélhetünk.
A merőleges irányú transzlációnak van egy további rendkívül fontos hatása: a részecske sugara a fény sebességével növekedni fog [10]. A sugár viszont meghatározza a forgási frekvenciát, ami fokozatosan csökkenni fog, ez pedig egyúttal a tömeg elvesztését idézi elő. A gyönge kölcsönhatási bozonok sorsa így a gyors eltűnés, de ez a forgás lassulása kivált egy újabb tehetetlenségi erőt, amit Euler mutatott ki. Amikor egy kereket felpörgetünk, akkor a forgási frekvencia megváltozása a centrifugális erővel ellentétes irányú tehetetlenséget idéz elő. Fénysebességű forgások esetén a forgástengelyre merőleges irányú és fénysebességű transzláció épp akkora Euler-erőt hoz létre, mint a centrifugális-hatás [11]. A W bozon úgy kapcsolódik a fermionhoz, hogy változó forgási frekvenciája révén „áthangolja” a fermiont egy másik saját frekvenciára, azaz létrehoz egy új típusú részecskét. Gyorsuló forgáskor az Euler-erő teljesen kiegyenlíti a centrifugális erőt, amiért a spirális forgást végző W bozon energia felvétel nélkül létrejöhet, ha megkapja a „kezdő lökést” (impulzusmomentumot), amikor egy fermion spin vetületi kvantumszáma -½-ről ½-re változik. Ezzel szemben a foton emisszióhoz nem csak a vetületi kvantumszám változása által létrehozott „lökésre” van szükség, hanem a fermion energiájának változására is. Az emittált foton, amíg nem lép kölcsönhatásba egy másik fermionnal, megtartja forgási frekvenciáját, azaz energiáját. Más a sorsa a gyenge kölcsönhatás bozonjainak. Ekkor a spirális mozgás lassuló jellege miatt az Euler- és centrifugális-erő összeadódik, és így a tér görbületi energiája (az erős gravitáció) nem elegendő ahhoz, hogy stabilizálja a W bozon sajátforgását, és kellő kompenzáló erő hiányában a bozon gyorsan eltűnik.
A rövid élettartam miatt a W bozon csak rövid távolságot tehet meg, ami megmutatkozik a gyenge kölcsönhatás rendkívül rövid hatótávolságában is. A kölcsönhatás ereje sok nagyságrenddel elmarad az elektromágnesestől, emiatt a kettős univerzumban, melyben a részecskék világa kapcsolódik a sajátmozgást stabilizáló görbült tér világával, a gyenge kölcsönhatás gyenge kapcsolatot épít fel a két „világ” között. Emiatt van, hogy megmaradási törvényeink érvényesek a részecskék átalakulási folyamataiban. A W és Z bozonok megjelenése csak egy rendkívül rövid intermezzo, amelyik az energia megmaradás törvényét megszakítja és a bozonok eltűnésével az energiamegmaradás törvénye helyre áll.
A W bozon tömegváltoztató képessége teszi lehetővé, hogy egymásba alakuljanak a különböző tömegű fermionok kemény gamma-sugárzás kibocsátása nélkül. Ez történik például, amikor az elektron „nagytestvérei”, a müon és tauon átalakulnak elektronná a gyenge kölcsönhatáson keresztül [12]. A W bozon „élete végén” meg kell, hogy szabaduljon impulzusmomentumától és töltésétől, ami azáltal következik be, hogy két fermion, azaz egy elektron és egy neutrínó keletkezik a W bozon eltűnésekor. Ez az átalakulás akkor következik be, amikor létrejönnek azok a rezonancia feltételek, amelyek szükségesek a kettősforgás megvalósulásához, mert emlékezzünk rá: amíg a foton bármekkora frekvenciával foroghat az elektron csak nagyon pontosan rögzített tömeggel, azaz forgási frekvenciával rendelkezik.
A W bozonokon kívül létezik a töltés semleges gyenge kölcsönhatási bozon is, amit a Standard Modell Z szimbólummal jelöl. Ennek szerkezetéről majd a neutrínók átalakulási folyamataival kapcsolatban fogunk írni.
Foglaljuk össze az elmondottakat! Az elektro-gyenge kölcsönhatást úgy tekinthetjük, mint ami három alapvető mozgásformát – gömbforgásokat (fermionok), csavarmozgásokat (fotonok) és spirálmozgásokat (W és Z bozonok) – kapcsol össze. Két gömbforgás között csavarmozgások közvetítenek, az egyik gömbforgást a másikba spirálmozgások visznek át. Két azonos frekvenciájú, de ellentétes kiralitású gömbforgás eltűnhet (annihiláció), miközben csavarmozgást hoznak létre, de a csavarmozgás is átalakulhat az előbbi két gömbforgásba (párképződés). A gömbforgásnak a sajátfrekvencia megváltozása nélküli állapotváltozása hozza létre a csavarmozgásokat (foton emisszió), míg ha a sajátfrekvencia is megváltozik, akkor spirálmozgás keletkezik (W emisszió). A spirálmozgás pedig szétszakad két különböző kiralitású gömbforgássá (W eltűnés).
A részecskék világát a görbült tér háttér világával a gyenge kölcsönhatás kapcsolja össze. Ez a kölcsönhatás egyrészt gyönge, másrészt ideiglenes, csak a W és Z bozonok rövid élettartamáig tart. Amikor ezek a részecskék eltűnnek, akkor a részecskék ugyan átalakulnak, de a teljes energia változatlan marad. Tehát a kapcsolat tranziens jelenség, amely során a részecskék által átmenetileg felvett energia és tömeg teljesen „visszaadásra” kerül. Emiatt van, hogy a részecske világra az energiamegmaradás törvénye külön is érvényes, ha eltekintünk ettől a rövid intermezzótól.
Az ismertetett modell tehát az elektro-gyenge kölcsönhatás minden folyamatára szemléletes képet kínál, ily módon támasztva alá azt a koncepciót, hogy a részecske világ alapja a fénysebességű sajátforgás.
Az elektromágneses és gyenge kölcsönhatás kapcsolatát illusztráljuk egy szemléletes példával. Képzeljük magunk elé a tengert, amiben egy hajó úszik. A hajó nem süllyed el, ami azArchimédesz által megállapított törvénynek köszönhető. A hajó egy bemélyedést (görbületet) hoz létre a vízben, a kiszorított víz súlya egyenlíti ki a hajó súlyát. Ennek analógiájára képzelhetjük el a teret, ahol a részecske forgása görbületet hoz létet és ez a görbület ellensúlyozza sajátforgásának kifelé perdítő hatását. Most vegyünk fel egy szemüveget, amelyikkel nem látjuk a tenger vizét csak a hajót. Ekkor úgy tűnik, hogy a hajó az üres térben lebeg. Valójában ez a helyzet, amikor tanulmányozzuk a részecskék mozgását, hiszen a fotonok nem adnak felvilágosítást a részecskéket magában foglaló térről és annak görbületeiről. Most cseréljük fel a szemüveget egy olyanra, amivel nem látjuk a hajót, csak a tenger vizét. Ekkor viszont egy hajó formájú bemélyedést fogunk látni, ahogy tovább halad. Ennek felel meg, amikor információt nyerünk a görbült tér szerkezetéről a gyönge kölcsönhatási bozonok detektálása révén.
[8] Az elemi részecskék tömegét MeV illetve GeV egységben szokás megadni, amely az elektron energiáját fejezi ki 1 millió, illetve 1 milliárd Volt feszültségű elektromos térben. Az elektron tömege 0,511 MeV, a protoné 1,007 GeV, a W bozoné 80,385 GeV, a Z bozoné 91,188 GeV, tehát a gyenge kölcsönhatási bozonok tömege hozzávetőleg 100-szor nagyobb a protonnál és 200 000-szer nagyobb az elektronnál
[9] A Standard Modell szerint a béta-bomláskor antineutrínó keletkezik, de nincs egységes álláspont, hogy tényleg különböző részecske lenne-e a neutrínó és az antineutrínó, ezért a szövegben csak neutrínóról beszélünk
[10] Fénysebességű forgások esetén ω = c/r és m = ℏω/c2
[11] Az Euler-erő a szöggyorsulással arányos: m.r.dω/dt és iránya azonos a centrifugális erővel lassuláskor, viszont ellentétes gyorsuláskor. A fénysebességgel táguló spirálmozgás során az szorzat állandó marad és így . Ebből következik, hogy az Euler-erő kifejezése: -m.ω.c lesz, ami megegyezik a centrifugális erővel.
[12] A müon tömege 106 MeV, a tau részecskéé 1777 MeV. Ezek a részecskék az elektronnal azonos kiralitású kettősforgást végeznek, de forgási frekvenciájuk nagyságrendekkel nagyobb és emiatt centrális sugaruk kisebb. Ez arra mutat, hogy a téridőnek létezik két magasabb forgási frekvenciájú gerjesztett állapota is. A két magas frekvenciájú gerjesztett állapot valamennyi elemi fermion (pozitron, neutrínó, kvarkok) esetén megfigyelhető, a Standard Modell ezért három részecske generációt különböztet meg.
A neutrínó és a Z bozon: szuperponált királis forgási állapotok
A fermionok családjába tartozó neutrínó nem rendelkezik elektromos töltéssel, ugyanez érvényes a gyenge kölcsönhatás részecskéi közül a Z bozonra is. A neutrínó S = ½, a Z bozon az S = 1 spinje úgy értelmezhető, hogy az előbbi kéttengelyű, az utóbbi egytengelyű sajátforgást végez, de hogyan magyarázzuk a töltés semlegességet? Kiindulópontunk a kvantummechanika egyik alapelve: ha két mikro-rendszer azonos energiával rendelkezik valamilyen szimmetria miatt, akkor a két állapot szuperpozíciója is leírja a rendszer állapotát. Erre az elvre támaszkodik a Standard Modell is, amikor osztályozza a kvarkokból felépülő mezonokat és barionokat, ezért összhangban maradunk a szokásos részecskefizikával, ha ezt az elvet alkalmazzuk a két királis sajátforgás esetében is. Amíg az elektron és pozitron a jobb illetve balsodrású királis forgást végez, addig a neutrínóban a két királis állapot egyenlő súllyal szerepel és ezért töltés semleges lesz. Ugyan ez tételezhető fel a Z bozon esetén is, ott a W- és W+ forgások egyenlő szuperpozíciós súlya vezet nulla töltéshez.
Az elektronhoz és a később tárgyalandó kvarkokhoz hasonlóan a neutrínóknak is három alaptípusa, un. generációja van, amit elektron, müon illetve tau típusú részecskének neveztek el. Elektronok és kvarkok esetén az egyes generációk tömegükben, azaz sajátfrekvenciájukban különböznek. Neutrínók esetében azonban nem sikerült a nyugalmi tömeget meghatározni, erre csak felső becslést lehetett adni a terjedési sebességük alapján. A neutrínók kimutatása a béta-bomlás folyamatának megfordításával történik, amikor a neutrínók protonokból neutronokat hoznak létre, amihez már eleve nagy energiájú részecskékre van szükség. Az eddigi kísérletek valamennyi esetben a fénysebességhez igen közeli haladási sebességet találtak [13], amiért az is feltételezhető, hogy a neutrínók egyáltalán nem rendelkeznek nyugalmi tömeggel. Ennek ellentmondani látszik az a megfigyelés, hogy a kozmikus sugárzásban a három típus egymásba alakul át, amit neutrínó oszcillációnak neveztek el [14].
A Standard Modell eredetileg nulla tömeget rendelt a neutrínók számára, mert ez összhangban van avval, hogy a neutrínók sebessége c, de ennek ellentmondani látszik a neutrínó oszcilláció, ahol éppen a tömegkülönbségek játszanak szerepet. Véleményem szerint az ellentmondás a tömeg és evvel együtt az elektromos töltés fogalmának újraértelmezésével megoldható. Ennek kiinduló pontja az elektron relativisztikus kvantumelmélete, amit Dirac alkotott meg [15]. A Dirac-egyenlet általánosításával kapott fermion egyenletben a forgások kétdimenziós királis terében kétszer-kettes mátrixok reprezentálják a tömeget és az elektromos töltést (lásd később). A mátrixok diagonális elemei határozzák meg a részecskék fizikailag mérhető tömegét és töltését, amely nulla neutrínók estén, míg a kvarkok esetén a töltésre ±1/3 és 2/3 értékek adódnak ki. Neutrínóknál és kvarkoknál a tömeget reprezentáló mátrixnak vannak nem diagonális elemei is és ezáltal lehet értelmezni a három fajta neutrínó eltérő tulajdonságait az oszcillációs jelenséget is beleértve.
[13] Nagy szenzációt okozott az a bejelentés, amikor egy kísérletben azt találták, hogy a neutrínók haladási sebessége meghaladja a fényét. Utóbb azonban a kísérleti körülmények ellenőrzése során kiderült, hogy az eredmény téves és a sebesség megegyezik a fényével a mérés pontossági határain belül. A fénynél nagyobb sebességet a kvantumelektrodinamika elmélete virtuális folyamatokban ugyan feltételez, mert ezáltal lehet bizonyos fizikai konstansokat értelmezni, de ezek a folyamatok csak a közelítő számításokban lépnek fel. Egyes kvantummechanika jelenségek esetén, amit EPR paradoxonnak neveznek Einstein, Podolsky és Rosen publikációja nyomán, olyan interpretációk is vannak, ahol nincs sebességkorlátja a kölcsönhatásnak. Evvel kapcsolatban szerepel a honlapon a „Determinizmus és kvantummechanika: a szabadság szintjei a fizikában” című írás.
[14] A neutrínó három alaptípusa kapcsolódik az elektron három generációjához (elektron, müon, tauon), keletkezési és átalakulási folyamataik egy generáción belül mennek végbe. A müon például első lépésben egy müon típusú neutrínóra és egy W- bozonra „hasad” szét. Itt a széthasadásról csak korlátozott értelemben beszélhetünk, mert a képződő W bozon tömege ezerszer nagyobb, mint a „kibocsátó” müoné. A W bozon eltűnik miközben egy elektron és egy elektron típusú neutrínó keletkezik. A két új részecske energiája azonban nem örökli a W bozon óriási tömegét, tehát a W bozon megjelenésével együtt járó nagy energia és tömeg csak átmenetileg növeli meg a részecskevilág energiáját. A neutrínók három típusának egymásba alakulását (oszcillációt) a Napból származó és magfúziós reakciók során kibocsátott neutrínók számának a vártnál jóval kisebb fluxusa miatt tételezik fel. Az oszcilláció elméletében feltételezik az egyes generációk különböző tömegét és ezek négyzetes különbsége határozza meg az oszcillációs hullámhosszat.
[15] A relativitáselmélet négyzetes összefüggést állapít meg az impulzus és a nyugalmi energia között, ami az elmélet egyik kovariánsa. Ide bevezetve az impulzus és energia kvantummechanikai operátorát az energiára kvadratikus kifejezést kapunk. De az operátorszámítás alapját képező sajátérték egyenlet lineáris formulát követel meg, amit Dirac azáltal oldott meg, hogy a négyzetgyökvonás műveletét négydimenziós mátrixokkal (spinorokkal) végezte el. Ezek a spinorok felbonthatók a kétdimenziós Pauli-mátrixok szorzatára, ahol az egyik tényező a spin definícióját adja, a másik pedig leírja a pozitív és negatív energiájú megoldásokat. A Pauli-mátrixok komplex számokból épülnek fel, de a két diagonális elem valós szám, amely megadja a spin z komponense két sajátértékét, illetve az energia és tömeg előjelét. Dirac módszerét tovább fejlesztve a négyzetgyökvonást 8*8 elemű spinorokkal is elvégezhetjük, ekkor fellép egy harmadik 2*2-es mátrix, amelynek valós diagonális elemei definiálják a neutrínók és kvarkok tömegét illetve töltését. Ez az általános fermion egyenlet egységes keretek között tárgyalja az elektront, pozitront, az neutrínót, valamint a kvarkok két alaptípusát (up és down) is, tehát kiterjed a Standard Modellben leírt valamennyi elemi fermionra.
Kvarkok és gluonok a Standard Modellben
A Standard modell a kvarkok két alaptípusát (flavour) különbözteti meg, az „up” típus elektromos töltése 2/3e, a „down” töltése -1/3e. A proton +e töltése két „up” és egy „down” kvark töltéséből adódik ki, míg a neutron esetén két „down” és egy „up” töltése hozza létre a semlegességet. A törttöltések bevezetését az indokolta, hogy a több száz kísérletileg megfigyelt mezon és barion szerkezete egyértelműen felépíthető két illetve három kvarkot tartalmazó struktúrákból. A kvarkok két típusának van antirészecske párja, amelyek töltése fordított előjelű, azaz -2/3e és +1/3e az „up” illetve „down” esetén. Amíg az összetett felépítésű mezonokban mindig egy kvark és egy antikvark található, addig a barionokat három kvark, az antibarionokat három antikvark építi fel. Minden kvarktípusnak három generációja van, ahol a magasabb generációk tömege jóval nagyobb és a belőlük felépíthető mezonok és barionok élettartama pedig jóval rövidebb. A kvarkok összes száma ezért 12. A különböző generációhoz tartozó kvarkok is kombinálódnak a mezonok és barionok felépítésében.
A spinek összeadási szabálya szerint két S = ½ spin létrehozhat S = 1 triplett, illetve S = 0 szingulett állapotot. Ennek megfelelően beszélünk szingulett és triplett mezonokról. A Pauli-féle kiválasztási szabály nem engedi meg, hogy egy kvantummechanikai rendszerben két fermion valamennyi kvantumszáma megegyezzék. Mezonok esetén ez nem jelent megszorítást, mert azt mindig egy kvark és egy antikvark hozza létre. A barionokban már három kvark kapcsolódik össze, ekkor a spin összeadási szabály S =1/2 illetve 3/2 eredő spint hozhat létre. Az utóbbi esetben a három kvark spin vetületi kvantumszáma megegyezik, de ez a Pauli-elv szerint csak különböző generációjú vagy típusú kvark esetén megengedett. Ennek ellenére találtak olyan rövid élettartamú barionokat, amelyek három azonos kvarkból épülnek fel. Emiatt vált szükségessé, hogy bevezessenek a kvarkok számára egy új kvantumszámot, amit szimbolikusan „színnek” nevezték el. Ennek oka, hogy ez a kvantumszám nem játszik szerepet az összetett részecskék esetén, azaz ekkor a komponensek eredő színe kioltódik, akár csak a három alapszín együttese, amikor kialakul a fehér szín. Mezonok esetén minden szín a „komplementerével” találkozik, ami színkioltáshoz vezet, viszont barionoknál a kioltás úgy jön létre, hogy három különböző alapszín tartozik a három felépítő kvarkhoz, és így az optikához hasonlóan a színek együttese „fehér” lesz.
Az elektro-gyenge kölcsönhatás elméletéhez hasonlóan kidolgozták a kvarkokat összetartó erős kölcsönhatás mezőelméletét, amit kvantum-szindinamikának neveztek el, arra utalva, hogy a kölcsönhatás a kvarkok „színétől” függ. Ebben az elméletben a gluonoknak nevezett részecskék közvetítik a vonzóerőt. Mivel három szín van így két kvark kapcsolatát 3*3 színkombináció írja le, amiért elvben 9 féle gluon közvetíthet a kvarkok között. A színkioltást színek és komplementerük kombinációi hozzák létre, de ezek között van egy olyan kombináció is, amelyik már önmagában is „fehér”, ezért ezt a lehetőséget kizárják az elméletben, végeredményben ezért 8 különböző típusú gluon írja le az erős kölcsönhatást. A gluonok a fotonhoz és a W illetve Z bozonokhoz hasonlóan S = 1 spinnel rendelkeznek.
A kvarkok vibrációs modellje
A kvark-elmélet neuralgikus pontja, hogy törttöltésű elemi objektumot nem lehetett megfigyelni még a nagy energiájú kozmikus sugárzásban és ütközési kísérletekben sem. Ezt a „bezártság” elvvel magyarázzák: két vagy három kvark szétválasztásához olyan nagy erőre lenne szükség, amely nem áll rendelkezésre sem a kozmikus sugárzásban, sem a gyorsítókban. Úgy képzelik el, hogy növelve két kvark távolságát a köztük ható vonzóerő is növekedni fog. Ebből a szempontból tehát pont fordítva viselkedik az erős kölcsönhatás, mint a gravitáció, vagy az elektromos töltések közötti erő. Ilyen típusú erő lép fel viszont a molekulákban két atom között a kémiai kötés révén. Ez az erő viszont vibrációt hoz létre az atomok között. A kvantummechanika fontos megállapítása, hogy az elemi rendszerek vibrációja semmilyen körülmények között nem „fagy be”, ezt hívják nullpont rezgésnek. Ezt a kvantummechanikai elvet a kvarkmodellre alkalmazva arra a következtetésre kell jussunk, hogy a mezonokban és barionokban kötött kvarkok is vibrációt végeznek! A vibráció a tér mindhárom irányában végbemehet, ezért logikus magyarázatot kapunk, hogy miért létezik éppen három szín, hiszen ezeket a színeket a vibrációkkal lehet azonosítani. A barionok „fehér színét” az okozza, hogy a benne levő három kvark a tér három különböző irányában rezeg, ami összességében gömbszimmetriát hoz létre. Mezonoknál viszont a két kvark ellenütemben végzi a vibrációt, ami megfelel a komplementer szín definíciójának. Önmagában ugyanis minden megfigyelhető részecske izotróp, azaz iránytól független objektum!
A neutrínók esetében már említettük, hogy a kvantummechanikai szuperpozíciós elv miatt létrejöhet olyan kettősforgás, ahol a két királis állapot együtt van jelen. Neutrínók esetén egyeznek a súlyfaktorok, kvarkokban különböznek. A súlyfaktorok segítségével a Standard Modell valamennyi objektumát jellemezhetjük: Az egyes részecskék töltése:
pozitron: 6/6→ jobb + 0/6→bal, töltés: +e
up: 5/6→jobb + 1/6→bal, töltés +2/3e
anti-down 4/6→jobb + 2/6→bal, töltés: +1/3e
neutrínó: 3/6→jobb + 3/6→bal, töltés: 0
down: 2/6→jobb + 4/6→bal, töltés: -1/3e
anti-up: 1/6→jobb + 5/6→bal, töltés: -2/3e
elektron: 0/6→jobb + 6/6→bal, töltés: -e
A szemléletesség kedvéért a súlyfaktorokat hatodokban adtuk meg. Itt a jobb és bal a két kiralitást jelöli, természetesen önkényes, hogy melyikhez rendeljük a pozitív és melyikhez a negatív töltést. A súlyfaktorokat az általános fermion egyenlet töltésre és tömegre vonatkozó 2*2-es mátrixaiból képezhetjük [16].
De miért „ragaszkodik” a természet épp a hatodokban kifejezett súlyfaktorokhoz, hiszen a szuperpozíciós szabály tetszőleges faktorokat is megengedhet. A kvark-antikvark összetételű mezonok töltése lehet nulla vagy ±e. Az első eset nem jelent megszorítást a királis súlyfaktorra, a másodok pedig csak annyit követel meg, hogy a két kvarktípus (up és down) súlyfaktorainak összege egységnyi legyen. A három kvarkból felépülő barionok töltése lehet nulla, ±e vagy ±2e. Ekkor a különböző töltések úgy adódnak ki, ha a fenti „hatodokat” tételezzük fel a két alap kvark számára. Tehát azért „választja” ki a természet a fenti királis arányokat, mert nem produkál olyan összetett elemi objektumot, amely háromnál több kvarkból épülne fel [17]. Az elektron, pozitron és neutrínó is illeszkedik a képbe, ha hatodokban írjuk fel a szuperpozíciós arányokat.
Az eddigiekben minden egyes fizikai kölcsönhatást valamilyen tehetetlenségi erővel magyaráztunk, de milyen tehetetlenségi erő kapcsolható az erős kölcsönhatáshoz? A mezonokban és barionokban lévő kvarkokat úgy képzelhetjük el, hogy koncentrikus héjszerkezetet alkotnak, akárcsak az elektronok az atommag körül. A fotonok által közvetített elektromágneses kölcsönhatás a királis kettősforgások közötti „külső” kölcsönhatás. Az egymásba ágyazott kvark struktúrák viszont közvetlenül érintkeznek, ezért közöttük a Coriolis-csavaró erő csillapítás nélkül hat. Ez azt jelenti, hogy az erős kölcsönhatás nem csökken le a Sommerfeld-féle finomszerkezeti állandó mértékében, ami összhangban van a kvantum-színdinamika egyenleteivel.
A héjstruktúra valamilyen irányú deformációja gyöngíti a héjak közötti átfedést és így a csavaró hatást, ami a deformáció növekedésével arányos erőt hoz létre, ami egymáshoz húzza a forgási héjakat. Ez az erő vibrációkat idéz elő a héjak között, amit a Standard Modell a gluonnak nevezett közvetítő bozonokkal ír le. Ez a bozon az egyik vibrációt kioltja (komplementer szín), a másikat felépíti (szín), ezért a vibráció két alaptípusának szorzatából épül fel a nyolctagú gluonok családja. A bozonok S = 1 spinjét a korábbiakban egytengelyű forgásokkal értelmeztük. Ebben az esetben a forgásoknak rezgések felelnek meg, mert a rezgés mindig felfogható, mint egy forgómozgás vetülete. A kölcsönhatás távolságát a héjak Compton-sugara határozza meg, innen fakad az erős kölcsönhatás rövid hatótávolsága.
Magyarázatra vár még, hogy miért nincs elektronok, pozitronok és neutrínók esetén erős kölcsönhatás? Neutrínók esetén azért, mert az egyenlő súlyú királis héjak közötti tartományban a Coriolis-hatás kompenzálódik, elektron és pozitron esetén pedig csak egyetlen királis héj létezik, tehát nincs ami között felléphetne a „belső” Coriolis-hatás.
A Standard Modell az erős kölcsönhatás alapján osztályozza az elemi fermionokat egyrészt leptonokra (elektron, pozitron és neutrínó), másrészt kvarkokra. Osztályozhatjuk az elemi objektumokat a királis héjak száma szerint is, mert evvel a mezonokat és a barionokat is belefoglalhatjuk a képbe. Ekkor az elektront és pozitront tekintjük egyhéjú részecskének, a neutrínó és a kvarkok képviselik a kéthéjú objektumokat, a mezonokban a héjak száma négy, a barionokban hat.
[16] A szuperponált állapotot leíró állapotfüggvényben a részállapotokat (itt |Jobb> és |Bal>) leíró függvényeket valószínűségi amplitúdókkal szorozva adjuk össze: f = cosα.|Jobb> + sinα.|Bal> Egy adott fizikai mennyiség, például az elektromos töltés értékének meghatározásakor a töltésoperátor, amit a Q11 = -Q22 = e és Q12 = Q21 = 0 mátrix definiál, f függvénnyel alkotott várható értékét kell képezni, amely q = e.cos2α érték lesz. A pozitrontól elektronig terjedő hét részecskét az n kvantumszámmal értelmezve cos2a=(n+3)/3 definícióval, ahol n = 3, 2,1, 0,-1, -2, -3, valamennyi részecske töltését megkapjuk. Az n = 0 esetben, tehát a neutrínónál cos2α = 0, ezért nulla a töltés. Az általános fermion egyenletben definiált tömegmátrixban ekkor M11 = M22 =0 és M12 = M21 = m0 lesz, tehát nincs „diagonális” tömeg, de létezik nem-diagonális tömeg. Ez úgy fogható fel, hogy átlagértékben a tömeg nulla, de a tömegnek létezik statisztikai szórása, mert egyenlő valószínűséggel vesz fel negatív és pozitív értéket. Itt érdemes arra utalni, hogy az elektron Dirac-egyenletének vannak pozitív és negatív energiájú és ennek megfelelően pozitív és negatív nyugalmi tömegű megoldásai, bár az utóbbi kísérletileg nem lehet megfigyelni. További sajátsága a neutrínónak, hogy impulzusa diagonális, azaz P11 = -P22 = p0 és P12 = P21 = 0. Ezt úgy mondhatjuk, hogy a neutrínó tisztán „impulzus” részecske, szemben az elektronnal és pozitronnal, amelynek van nyugalmi tömege, de nincs nyugalmi impulzusa. Más megfogalmazásban ez azt jelenti, hogy a neutrínónak van kinetikus energiája, de nulla a nyugalmi energiája. Kvarkok esetén viszont olyan kevert királis állapotról kell beszélni, amelyik nincs sem nyugalmi tömegállapotban, sem nyugalmi impulzusa





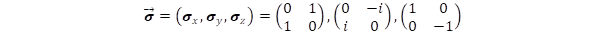
 és
és