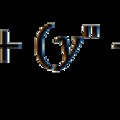A screw model for quantum electrodynamics: From gravitation to quanta

Facebook Tweet Tetszik

2015. július 13. - 38Rocky

"This accepted author manuscript is copyrighted and published by Elsevier.

It is posted here by agreement between Elsevier and MTA. The definitive

version of the text was subsequently published in [Ind. J. Phys., 89, 389-396 (2015)

date, DOI: 10.1007/s12648-014-0598-z]. Available under license CC-BY-NC-ND."

A screw model for quantum electrodynamics: From gravitation to quanta

A Rockenbauer*

Department of Physics, Budapest University of Technology and Economics and

MTA-BME Condensed Matter Research Group, Budafoki ut 8, 1111 Budapest, Hungary

Abstract

A screw model is developed for photons and fermions to offer a physical representation for the Feynman’s arrow scheme in quantum-electrodynamics. This model interprets intrinsic parameters of particles: spin, rest energy and magnetic moment by self-rotations with the speed of light forming either a helical (boson) or a spherical (fermion) screws. Due to the extreme Lorentz contraction the surface of screws is zero, while the radius remains finite (Compton radius). According to the general theory of relativity, the non-Euclidean geometry of space-time caused by the self-rotation of particles should produce an intrinsic force, which is analogous to the gravitation, but being 32-42 orders of magnitudes stronger, we denote it as strong gravitation. It is a self-stabilizing force for the intrinsic rotations, which is the source of spin and defines the Planck constant. The spherical screws of fermions are formed by double rotations, where the two rotations have right or left-handed chirality representing the particles and anti-particles. The double-rotation produces Coriolis force, where the sign is determined by the chirality and this force is the origin of electric charge. Parity violation in the beta-decay of neutrons is related to the symmetry of reflection for the self-motion of particles. The finite radius of self-rotation may resolve also divergences in the theory of quantum-electrodynamics.

Keywords: Feynman’s arrows; QED; self-motion of particles; strong gravitation

PACS (2010): 11.30.Er; 12.10.-g; 12.20.-m; 13.40.Em; 14.60.Cd

Corresponding author, e_mail: rockenbauer.antal@ttk.mta.hu

Introduction

Quantum electrodynamics (QED) constitutes an excellent mathematical method to describe the interaction mechanisms of light and matter [1]. Feynman describes the complicated quantum mechanical calculations by a visual model built up from a lot of arrows representing the photons. He characterizes the direction of arrows by the hand of an imaginary stopwatch that can time a photon as it moves. The movement of light is given by the summation of arrows rendered for the individual events and the probability of the final event is calculated as a square of the final arrow. In this paper we take an effort to find a physical representation for the arrows of Feynman in order to offer explanation for certain conceptual questions of quantum mechanics, like the origin of intrinsic parameters as the spin and the rest mass.

The Standard Model of elementary particles gives a complete description for the properties of elementary objects including fermions (leptons, quarks, hadrons) and the interaction mediating bosons as well as mesons [2]. The model is based on field theories for electromagnetic, weak and strong nuclear interactions (quantum chromodynamics, QCD), but it fails developing a consequent quantum field theory for gravitation. Another problem of field theories is that in the perturbation treatment infinite terms appear when the self-energy of particles is computed. In this paper we raise the question whether this mathematical problem is not related to the assumption of point like particles? The point like nature is proved by the scattering experiments of Bhabha [3, 4]. But how could a point like object have moments, like spin and magnetic dipoles? The Standard Model escapes this contradiction defining the spin as an “intrinsic” property. We point out how the contradiction between the concepts of point-like and finite size of elementary particles can be resolved by utilizing the formulas of special theory of relativity for motions with the speed of light. The key point of our analysis is an assumption for the self-motion of particles, which takes place on screw orbits (cylindrical or spherical) with the speed of light. We base this model on rotating frames by applying principles of the special and general relativity and point out that the rotating frames can be considered as the source of gravitation as well as the mass of elementary particles. This concept leads us for the assumption of a new form of gravitation that we call as strong gravitation, which force can stabilize the self-rotation of elementary particles. The question is raised whether the screw model can explain the origin of quanta and electric charge, and a proposal is made how to overcome divergence in quantum electrodynamics [5].

There are a few alternative classical models for the dynamics of electrons. Barut [6] has described the Dirac electron by representing the spin as an orbital motion due to the zitterbewegung. This model, however, can be hardly extended for photons and other bosons, which constitutes our major target. Rivas [7], on the other hand, has developed a mathematical model, where the dynamics of electrons can be described in terms of the evolution of the point charge. This suggestion contradicts with our approach based on the finite size of elementary particles. Ghosh [8] has studied in detail how the charge rotating at relativistic speed can account for the electromagnetic mass. None of the above mentioned works have raised the question of what force can stabilize any kind of self-rotation of the particles.

Theory
1. Rotating frames in special relativity

The theory of special relativity is developed for inertial systems moving by constant speed, while the general relativity is based for linearly accelerating frames [9]. In this work we focus our attention to other type of accelerating system, where the frame manifests rotation with constant speed. As customary we denote the axis of rotation by z, and ω = 2π.ν is the angular velocity of rotation. The peripheral speed is u = 2π.ν.r = ω.r at the radius r. If this speed is close to the c speed of light, the perimeter contracts according to the Lorentz rule. This relation can be applied even if the frame is not inertial, since for infinitesimal sections the curvature can be neglected and the whole perimeter can be derived by integration

Perimeter = 2r.π[1 – (ω.r/c)²]^1/2 (1)

Let us define the relativistic radius r_rel as Perimeter/2π:

r_rel = r[1 – (ω.r/c)²]^1/2 (2)

Figure 1. The Lorentz contraction of peripheral radius due to rotation with the angular frequency ω, OB shows the central radius, AB the relativistic radius

The relativistic radius is smaller than the central radius, since the latter one is perpendicular to the motion and is not contracted as seen in Fig. 1. Consequently, the rotating frame has a non-Euclidean geometry. This phenomenon plays a crucial role, when we consider the basic concept of the theory of general relativity [9]. A particular property of rotation frame with a constant w frequency is its limited domain of space, since at the radius R_c = c/ω its perimeter becomes zero and for this reason in the outside domain, where r > R_c, no rotation can take place with this frequency. For the mass m inside the limited domain of rotating frame r < R_c, we can apply the rule of mass enhancement:

m_rel = m/[1 – [1 – (ω.r/c)²]^1/2] (3)

The contraction of peripheral radius is compensated by the increase of mass and thus their product is a relativistic invariant:

m_rel.r_rel = m.r = constants (4)

This invariance has an important consequence, since it allows a space point without mass gaining finite mass if the speed of rotation agrees with c.

2. Gravitation: curvature of space in rotating frames

The electromagnetic, strong- and weak nuclear forces are successfully described by quantum field theories assuming special mediating bosons for each interaction, but no satisfactory quantum theory exists for gravitation. Though a boson is assumed, which is called as graviton [2], but no experimental observation supports its existence and no consistent theory has been developed. In the following we suggest a self-motion in a screw orbit for particles aiming to interpret both the intrinsic parameters of particles and the origin gravitation. For this double purpose we assume two kinds of rotation of space points: a rapid primary motion with the peripheral speed c at the radius R_c, which creates the spin and mass, and a slow secondary motion outside this domain creating the force of gravitation. What essential is that both processes lead to the curvature of space-time, and while this curvature is extremely large at the radius R_c, it is very small outside this domain.

According to the general theory of relativity, the mass deforms the geometry of space-time, which in turn, is the source of gravitation. The question can be raised: what kind of mechanism deforms the space around the mass? To answer this question we assume an inductive effect of rapid self-rotation, creating a slow rotation outside the region of radius R_c. The general theory of Einstein describes the motions of large macroscopic objects, while our purpose is to develop a microscopic approach when the gravitation is directly related to the properties of elementary particles. For this reason we reverse the logical sequence applied by Einstein [10]. In his theory an equation is conceived, which is expressed in the curved coordinates of space-time, which at the first approximation can reproduce the Newton gravitation law. The validity of Einstein’s conception is proved so that his theory can explain minor deviations from the Kepler’s law in the planetary or stellar motion and describes well how the light moves beside massive objects, like the Sun. In our model we assume that the space points rotate at the distance R > R_c from a physical object with mass M according to second Kepler’s law:

γ.M = ω²R² (5)

Here γ = 6.673 x10^-11 m³/kg s² is the gravitational constant. This assumption is based on the fact that the planetary motion is independent on the mass of rotating objects. Thus even when its mass is zero, the rotation can exist. A particular feature of this rotation is the spherical symmetry, which is discussed later in the particle models. Due to the Lorentz contraction the peripheral radius r is smaller than the central radius R:

r = R[1 – (ω.R/c)²]^1/2 (6)

Due to the spherical symmetry the radial φ_gr (R) component can describe the curvature of space, which in turn gives the gravitational potential for the rotating object of the mass m:

V_gr = - φ_gr.m (7)

Without rotation no contraction takes place and the radial curvature should be zero. The dimension of space-time curvature can be chosen as c², thus the following trial function can be defined:

φ _gr (R) = c²[1-(r/R)²] (8)

Instead of the trial function (8), other φ (1-r/R) functions can be chosen, but it is the only function, which can reproduce the Newton law of gravitation when we take into account the relativistic contraction in Eq. (6) as well as Kepler’s rule in Eq. (5). Then as shown in Fig. 2 the curvature can be given as:

φ_gr (R) = ω²R² = γ.M/R (9)

Figure 2. Curvature of space geometry due to the self-rotation of particles, the drop of curvature at the Compton radius is 32-42 order of magnitude, the axes are given in arbitrary units with dimensions cm and , respectively

By this way we have arrived to the Newton-law:

V_gr = -γ.M.m/R (10)

From this equation Kepler’s law can be deduced, just we reconstructed our starting point. The essential point of this logic is that by postulating the trial function as Eq. (8), we have obtained a proper function for the curvature of space-time, which can derive the gravitational force balancing the inertial force in the rotating frame. Though we have used Kepler’s law without any relativistic corrections e.g. given by Schwarzschild [10], the same procedure can be repeated if we add further terms to the relation in Eq. (5). Since Eq. (8) can correctly describe the gravitation law, we can consider it as a proper expression for the curvature of space-time in rotating frames.

Result and discussion
1. Strong gravitation: extreme curvature for rotation with the speed of light

The great importance of Eq. (8) is that it can explain not only the usual gravitational force, but also the origin of mass. Imagine a rotation where the peripheral speed is equal to c, that is R = c/ω and r = 0. Let us substitute r = 0 into Eq. (8), then we obtain

φ_gr = c² and V_gr = -m.c² (11)

It means that the potential energy of this rotation is just equal to the rest energy of a particle with a mass m! This fact makes the screw motion as self-consistent, since the self-rotation of space points creates a centripetal force due to the curvature of space, which can completely counterbalance the centrifugal force created also by the same rotation. In this way the rotation of space points can stabilize itself. This lead us to the conclusion that the self-motion of space points rotating with the peripheral speed c can represent particles where the perimeter or surface is zero, and the kinetic energy is equal to the rest-energy: E_self = -V_gr = m.c². This model suggests that the whole mass of particles is produced by self-rotation, but later we points out that electromagnetic interaction can give also a minor contribution.

The rotational model of gravitation manifests a close analogy with the optical principle of light propagating in a trajectory with the least time. For massive objects the trajectory approaches the other massive objects, since in their surrounding the space is more contracted. The origin of strong gravitation is related to the trajectory of zero length caused by the self-rotation with the speed of light.

The strong gravitation represents the strongest force possible. Due to the attractive character of common gravitation its effect is added together and can be very strong when the density of mass is extremely large, like in the black holes. It cannot exceed, however, the strong gravitation, since the peripheral radius cannot be reduced further if this radius has already reached the limit, when it is zero. This condition can give an upper limit for the total mass of black holes.

The concept of strong gravitation can be considered as a corollary of Higgs theorem [11] for the origin of mass. While the principle of spontaneous symmetry breaking explains the first step for the formation of a massive particle, which is equivalent to the self-rotation with a speed of c, the strong gravitation offers the force necessary for sustaining this motion.

2. Types of screw motions

The fermions with S = ½ spin and bosons with S = 1 spin require different symmetries for the self-motion. For the former – as it can be seen from the Dirac equation [12] – the expectation values are <S²_x> = <S²_y> = <S²_z> = ¼, , but this equality of the three spin components is not possible for spin S = 1. The eigenfunctions of S = 1 transform under the L = 1 irreducible representation of rotation group, but a double group should be defined by the extension of rotation group with a 2π angle rotation, which is no more identity operation. This double group has also two dimensional irreducible representations, which can be assigned to the S = ½ spin. In the following subsections we show how the screw motion described by single rotations can represent the photons with cylindrical symmetry, and how the fermions, e.g. the electrons can be described by screws with spherical symmetry, which can be produced by two rotations.

3.2.1. Photons represented by cylindrical screws

In the screw model of photon, the particles are represented by a rotation of local space points propagating on the surface of a cylinder with the speed of light, the surface of a cylinder is zero and the central radius is determined by the frequency: R_c = c/ω. According to the theory of QED the photons can propagate each direction with the same probability, which means that the axis of screws has arbitrary direction. We postulate this screw motion as an analogue for the rotating arrows in described by Feynman [1], where the phase in the screw motion plays the same role as the hand of imaginary stopwatch.

One of the most important discoveries of modern physics is the equivalence of mass and energy, which should be valid also for the photons. For this reason the energy of photons can be expressed by the equivalent motional mass m:

ħ.ω = m.c² (12)

This definition yields zero rest mass m₀ due to the extreme Lorentz contraction:

m₀ = lim(u→c)[m(1- u²/c²)^1/2 ] = 0 (13)

It means that we can consider the vacuum as a medium without rest mass, but it has the potentiality generating motional mass if the speed of any space points is equal to c. The energy Eq. (12) of photon gives also the momentum and angular momentum. For the momentum: p = m.c = ħ.ω/c = ħ.k, for angular momentum: I = m.c.R_c = ħ.ω.R_c/c = ħ.

The screw can be either left- or right-handed representing the two polarizations of photons, which define the angular momentum by the spin: I_z = S_z.ħ = ±ħ.

The potential energy gives also the force of curved space stabilizing the self-rotation:

V_sgr = -ħ.ω = ħ.c/r and F_sgr = -ħ.c/r² (14)

We suggest the nomenclature “strong gravitation” (SGR) for the fundamental force, which is created by the extremely curved space, in order to make distinction from the usual (weak) gravitation. The ratio of these forces is around 10³² -10⁴² for elementary particles (see later). We consider Eq. (14) as a basic structural law of the space-time, which plays fundamental role for determining the intrinsic properties of other elementary particles, like the fermions (see in the next subsection).

It is of great importance to point out, that the strong gravitation prescribes the same angular momentum ħ for all photons independently of their energy. By the screw model of photon we suggest a new interpretation for the existence of Planck constant, which can be defined as a force constant of strong gravitation. Since the space-time has the same basic structure in the universe, the same relations determine the intrinsic parameters of photons anywhere. Consequently both the Planck constant ħ and the speed of light c are universal constants manifesting the homogeny of space in the whole universe.

2.2. Fermions represented by spherical screws

Fermions can also be defined by the screw motion of space points with c peripheral speed, but this motion takes place on the surface of a sphere instead of a cylinder. The spherical symmetry is necessary to explain the identical expectation values for the squares of the three spin components. While the symmetry of rotation for photons is cylindrical, which can be represented by a rotation around a single axis, for fermions the spherical symmetry requires double-rotation, where the axis of rotation also rotates on the same w angular velocity. For double-rotation the complete rotation covers two single circles, accordingly, we can define the two-dimensional angular frequency as a half of the usual ω angular frequency:

ϖ = ω/2 =π.ν (15)

There is, furthermore, a particular geometric feature of double-rotation, since this motion has chirality: it can be either left- or right-handed. The time-inversion cannot transfer the two chiral geometries each other contrary to the cylindrical rotation of photons, where the two polarizations are time-inverted motions. The chirality allows defining two types of fermions: particles and antiparticles, e.g. electrons and positrons. There is a conceptual advantage of this rotational model, since there is no need for defining a vacuum with totally filled negative energy states like in the Dirac model [12]. The positron is simply a geometric mirror image of the electron and not a hole in the sea of electrons with negative energies. This concept offers a straightforward explanation for the parity violation in the beta decay of neutrons: only the external motional coordinates are reflected in the process of neutron decay without affecting the self-rotation [13]. To obtain a complete reflection one has to substitute the neutron with antineutron, and also the emitted proton, electron and neutrino should be replaced by their respective antiparticle. This operation is termed as charge conjugation, which is equivalent in our model with the reflection of self-rotation.

Being the peripheral speed c, the central radius is R_c = c/ω. All properties of fermions can be deduced from the balance between the centripetal force of the strong gravitation and the centrifugal force of the double-rotation:

ħ.c/R²_c = 2m.ω²R_c = 2m.c²/R_c (16)

In Eq. (16) the centrifugal force has a factor 2, since the double rotation consists of two separate rotations with the angular frequency ω. This relation gives an angular momentum I_z = m.c.R_c = ħ/2. Due to the spherical symmetry of rotation: I²_x = I²_y = I²_z =ħ²/4, which yields I² = I²_x + I²_y + I²_z =3/4 ħ² in a complete agreement of the S = ½ spin in the Dirac equation [14]. The unusual 4π periodicity of S_z = ½ spin eigenfunction exp(±i.ϖ.t) = exp(±1/2 i.ω.t) is in accordance with the definition in Eq. (15), since the spin is defined in the space of the double-rotations. Thus the concept of double-rotation gives a logical explanation why the 4π rotation is defined as the identity operation in the double-group describing the transformation properties of systems including odd number of electrons [15].