Túra a makrovilág és a mikrovilág között
Nehéz túra megtételére invitálom az olvasókat, amelyben a valóság és a képzelet viszonyáról lesz szó. A túra nehézségét az adja, hogy gondolkodásunk alapvető pillérjeit kell átalakítani az út során. Ez az út számomra is sok nehézséggel jár, aminek többször is neki kezdtem. Egyik ilyen vállalkozásom címéül adtam Mark Twain regényének címét „A koldus és királyfit”. A makro és mikro világ kapcsolatát a koldus és a királyfi segítségével szimbolizáltam. A regény bemutatja, hogy a két szereplő milyen bonyodalmakba kerül, mert a két világ nagyon különbözően gondolkodik. Itt is arról lesz szó, hogy milyen nehézségek támadnak, amikor makro világunk „koldusaiként” akarjuk megérteni a mikrovilág királyi birodalmának titkait. Az útra magunkkal visszük szokásos fogalmainkat, amit a hétköznapi világ megismerésekor szereztünk, de a mikrovilág megértésére való törekvés szükségessé teszi, hogy átírjuk legfőbb fogalmainkat a valóságról, a valódiról és a valósról, és keresni kell a kapcsolatot a valóságról alkotott elképzeléseinkkel. Ennek során ellentmondások sorával találkozunk, ami szükségessé teszi a mikrovilággal konzisztens fogalmak megtalálását. Tapasztalatainkat hasznosítva indulhatunk visszafelé a felépítési elvet alkalmazva, amikor a mikrovilág elemeiből építjük fel a makrovilágot. Nem győzöm hangsúlyozni, hogy a logikai út követése komoly megpróbáltatás lesz az olvasók számra is. De vágjunk bele!
A valóság megismerésének útján
A legalapvetőbb kérdés, amire keressük a választ – legyen szó akár fizikáról, vagy filozófiáról – hogy mi a valóság, mi a megismerés. Ebben a kérdésben fordulatot hozott, hogy a XX. Század elején a fizika áttörést ért el a mikrovilág megismerésében, amikor megalkotta a kvantumfizikát. Ez viszont felvetett filozófiai kérdéseket is, kialakultak különböző iskolák, aminek tengelyébe a determinizmus kérdése került. A klasszikus fizika Newtontól kezdve determinisztikus képet alkotott, ezen az alapon áll az einsteini általános relativitáselmélet is, szemben a kvantummechanikával, amely felállította Heisenberg nyomán a határozatlanság elvet, mely szerint a mozgás során a pozíció és a lendület mérése egyidejűleg nem adhat végtelenül pontos értéket. A két mérés pontosságának szorzata nem lehet kisebb, mint a ћ Planck állandó. Vajon feloldható-e az ellentmondás a két elmélet között? Ebből kiindulva nézzük meg először, hogy mit is értünk az olyan fogalmakon mint a valóság, a valóságos, vagy a valós, és ezt állítsuk szembe a képzelet, a képzelt, illetve az imaginárius fogalmakkal. Keressük ennek a két fogalomcsokornak a kapcsolatát.
A képzelet a valóságról alkotott szubjektív képünk, amelynek alapvető szerepe van a megismerésben. Gondolatainkat indítsuk el egy bibliai történettel, amikor Tamás apostol kétkedett, hogy valóban feltámadt-e Krisztus. Ő nem volt jelen, amikor először jelent meg Krisztus az apostolok előtt, csak tőlük tudta meg a hírt. Kételkedett, hiszen ő is ott volt a Golgoták hegyén és saját szemével látta a kereszthalált. Emiatt arra gondolt, hogy csak a vágy vezette a többi apostolt, hogy szerették volna újra látni a Mestert, és ez a vágy megtévesztette őket és megalkotott egy víziót. Ő a megfogható valóságról akart meggyőződni, kezével kitapogatni Krisztus sebeit. Így akart meggyőződni a valóságról.
A világ megismerése állandó összehasonlítás a képzeletünkben megalkotott kép és a látott világ, vagyis a valóság között: csak akkor ismerünk fel valakit, ha már ott van képzeletünkben az előzetes kép.
A matematikai absztrakciók világa: műveletek és számrendszerek
Mi tehát a valóság és mi a képzelet, olykor csak átmenetek sorozata, melyben folytonosan halványulhat el a valóság és adhatja át helyét a képzeletnek, és ez az út gyakran megtehető fordítva is. Ennek az útnak legabsztraktabb formája a matematika. Beszéljünk erről a számok világában is! Hasznos lesz, amikor tárgyalni fogom a klasszikus makroszkopikus fizika és a mikroszkopikus világ fogalmi rendszerének kapcsolatát.
Az egyes számrendszerek definíciójában is kibontakozik a fokozatos átmenet a valóság és a képzelet világa között. Az egyes számok megalkotója a művelet, ami egyrészt létrehozza a számokat, másrészt kapcsolatba hozza őket. A szám az alany, a művelet az állítmány. A legősibb művelet a számlálás, például számba vehetjük, hogy hány diót találtunk, így alakul ki az 1,2,3 …. és innen felfelé. Ezeket nevezzük természetes számoknak. Azért természetes, mert közvetlenül kapcsolódik a természet megismeréséhez. De kialakíthatunk kupacokat a diók között, az egyikben legyen, mondjuk 3, a másikan 4. Az összegüket meghatározhatjuk egyesévek megszámlálva, de ha már előtte megszámoltuk, hogy 3 illetve 4 van bennük, akkor meggyorsíthatjuk a számbavételt az összeadás műveletével. Ez csak egy csoportosítást jelent, ami nem alkot meg új számrendszert, maradunk a természetes számok halmazánál. Ott lép be a matematikai absztrakció, amikor felvetjük az összeadás művelet fordítottját a kivonást. Ezt nevezzük az összeadás inverz műveletének. Az inverz művelet sajátossága, hogy kibővíti a számrendszerünket. Ha egy kisebb számból nagyobbat vonunk ki, akkor jutunk el a negatív számokhoz. A negatív és pozitív számokat együtt már egész számoknak nevezzük. De hozzunk létre egy új csoportosítást, amikor 3 elemből álló kupacokat csinálunk, mondjuk négyet. Ekkor ahelyett, hogy négyszer egymás után végeznénk el az összeadást, bevezetjük a szorzás műveletét. Maga a szorzás csak újabb csoportosítás, mi nem vezet ki az egész számok világából, de ha újra megfordítjuk a műveletet, eljutunk az osztáshoz is. Ez tovább bővíti a számrendszerünket, eljutunk a racionális számok világába. Ezt racionálisnak nevezzük, mert még nem távolodtunk el messze a természetből kiinduló művelettől. De a szorzást is megismételhetjük néhányszor, ezt nevezzük hatványozásnak. Ez is csak egy újabb csoportosítási elv, ezért ekkor még a racionális számok halmazánál maradunk. Megváltozik ismét a helyzet, ha megfordítjuk a hatványozást és bevezetjük annak inverzét a gyökvonást. Itt már újra kiegészül a számhalmaz, például ha 2-ből vonnunk gyököt. Ekkor olyan számhoz jutunk, ami nem állítható elő két egész szám hányadosaként. Ezzel kilépünk a racionális számok halmazából és irracionális számokról beszélünk. Ide már olyan számok is tartoznak, ami még gyökvonással sem adhatók meg. Ilyen ismert szám a pi, ami a kör kerületének és átmérőjének hányadosa. Összességében az eddigi számokat valós számnak nevezzük, amivel azt fejezzük ki, hogy a szokásos valóságból kiindulva tudjuk levezetni ezeket a számokat. De a matematika ezen is túl lép, amikor felveti a lehetőséget, hogy vonjunk gyököt a negatív számokból is. Ez a lépés már tényleg csak matematikai képzeletünk terméke, ezért ezt a terméket már imaginárius számnak nevezzük, aminek egysége az „i”, ami a -1-ből vont négyzetgyököt jelenti.
A matematikai képzelet itt sem áll meg, hanem megalkotja az összetett, két elemű szám fogalmát, ez a komplex szám, aminek egyik tagja valós, a másik imaginárius. Ez egy hasznos művelet a fizikában, ha két mennyiség szorosan összekapcsolódik, mint például az elektromos és a mágneses mező az elektrodinamikában, de erre találunk példát a kvantummechanikában is. A mikrovilág objektumait komplex függvénnyel tudjuk leírni, amelyben a valós és az elképzelt szorosan összetartozik, a kettő csak együtt értelmezhető. A teljes valóságban benne van saját elképzelésünk is a valóságról.
A matematikai összekapcsolás megindít egy új utat, amikor több mint két komponenst kapcsolunk össze. Három komponensről beszélünk, amikor a háromdimenziós tér vektorairól beszélünk. Eddig a művelet határozta meg a számokat, de itt megfordul a dolog: a háromkomponensű vektorok között már belép egy új szabály: a komponensek sorrendisége. Beszélhetünk az olyan szorzatról, aminek eredménye egy újabb vektor lesz, ez a vektoriális szorzás. Itt mar megszűnik az a szabály, hogy a szorzat két elemének közömbös a sorrendje, például 3-szor 4 szorzatnak ugyanaz az eredménye, mint a 4-szer 3-nak. Ez a kommutativitás. A vektoroknál már új helyzet álla elő: ha az x és y vektorok szorzata létrehozza a z-ét, ahol a három irány úgy igazodik egymáshoz, mint egy jobbsodrású x,y,z koordináta rendszer. Ezt jobb kezünkkel szemléltethetjük, ha az x irányt nagyújunk, az y-t a hüvelykúj, z-t felfelé mutató tenyerünk mutatja meg. Ha a szorzatban x és y-t felcseréljük, azaz y-t szorozzuk x-el, akkor az eredő z irány fordítva mutat, amit már balkezünkkel szemléltethetünk. Ez a kettőség a kiralitás, ennek van döntő szerepe, ha érteni akarjuk a Coriolis erőt, sőt a töltések kétféle előjelét, vagy az anyag és antianyag kettősségét is. A kommutativitás hiánya értelmezi a határozatlansági relációt is a kvantummechanikában, amikor kiderül, hogy a pozíció és a lendület szorzata nem határozható meg tetszőleges pontossággal. A három komponensű számkombinációhoz képest is tovább léphetünk, amikor mátrixokba rendezzük a számokat, ilyenek a tenzorok is, meg az operátorok. Talán unalmas lehetett ez a számelméleti kitérő, de sokat fog segíteni, amikor a klasszikus fizika és a kvantumfizika kapcsolatáról lesz szó.

Hol van az elválasztó határ a makro- és a mikrovilág között?
A fizikára visszatérve beszéljünk először a makroszkopikus és a mikro rendszerek viszonyáról. Hol van az elválasztó határ közöttük? Úgy tűnik, hogy ez a kérdés gyakran homályban marad, ami számos félremagyarázást eredményez. Erre ismert példa a Schrödinger macskája is.
Nézzük először a ködkamra felvételt, ami mágneses mezőben készült egy elektron útjáról, ami kissé növekvő sugarú körpályához vezet. Vajon ez a pálya már a mikrovilághoz tartozik? A válasz nem, noha egyetlen elektron útját mutatja, de makroszkopikus eszközökkel. A köd parányi elemei ugyan kisebbek egy milliméternél, de mégis csak makroszkopikus objektumok, minden egyes csepp víz molekulák trillióiból tevődik össze. Valójában az elektron által megváltoztatott ködcseppeket látunk, ez az elektron útjának nyoma. Tehát nem magát az elektront látjuk, csak azt a pályát, amit befutott. Az elektron minden egyes ködcseppel reagálva valamit lead lendületéből és energiájából, ezért a mágneses mező kissé növekvő sugarú pályára kényszeríti, de amikor ezt a pályát matematikailag leírjuk, nem a kvantummechanika törvényeit alkalmazzuk, hanem a klasszikus fizikáét, az elektrodinamika és a mechanika szokásos törvényeit. A mikrovilág törvényére, a kvantummechanikára akkor van szükség, ha az elektronokat egy molekulában, vagy egy kristályrácsban, vagy egy fémes vezetőben vizsgáljuk, ekkor beszélhetünk a részecske és hullámtermészet kettősségéről. A mikro és makrovilágot egy rendkívül kis és egy rendkívül nagy szám választja ketté: az egyik a ћ = s Planck állandó, a másik az Avogadró szám 6·1023. Ez azt jelenti, hogy a kvantum lépés nagysága rendkívül kicsi, észrevehetővé akkor válik, ha az Avogadro számú mikro-objektumról van szó. A kvantummechanika törvényei a korrespondencia elve szerint, akkor mennek át a klasszikusba, ha nagy az objektumok száma, vagy nagy a kvantumszám értéke. Ebben a határesetben már a klasszikus mechanika írja le a mozgásokat.

A láthatatlan stacionárius állapot
A mikrovilág törvényeinek megismeréséhez át kell alakítani gondolkodásunk egész fogalmi rendszerét. Hasonló a helyzetünk, mint amit Mark Twain regényében leírt, amikor a koldus a királyi udvarba került. Azok a fogalmak, melyek jól beváltak a koldusok között már nem voltak érvényesek a királyi udvarban, ami félreértések sorozatával járt. Az első, amit meg kell tanulni, hogy nem a mozgási pályát látjuk, hanem a különböző állapotok közötti ugrást. Valójában a pálya közvetlenül nem is látható, ezért stacionárius állapotokról beszélünk. Az ugrásokról a fény kvantuma, a foton ad információt. A bennünk kialakuló kép a mikrovilágról ̶ például a mérési pontosság ̶ attól függ, hogy milyen tulajdonsággal rendelkezik az információ közvetítője, a foton.
A klasszikus mechanika látható pályával rendelkezik, ami azt jelenti, hogy pontról pontra nyomon követhetjük akár egy bolygó vagy csillag pályáját teleszkóppal, vagy láthatjuk a labda ívét szemünkkel, de felvehetjük videóra is. Ezt tekintjük a valóságos pályának, aminek leírásához valós függvényt írhatunk fel. De mit tudunk mondani az elektron mozgásáról akkor, amikor nem bocsát ki fényt? Ekkor csak elképzelhetjük a pályát. Elképzelésünket azonban a valóságra alapozzuk, mert az ugrást már látjuk két állapot között, amiből visszakövetkeztetünk arra, hogy mi volt a kiinduló és mi a végső állapot. Az elképzelt, azaz imaginárius pályát már csak az imaginárius számot tartalmazó függvénnyel írhatjuk le. Így találkozik egymással az elképzelt pálya és annak matematikai leírása komplex függvénnyel.
Ennek az elképzelt pályának megtalálása a kvantummechanika feladata. Ennek a pályának új nevet adunk, úgy nevezzük, hogy ez az elektron állapota az atomokban és molekulákban. Mivel nem látjuk a pályát, ezért úgy vetjük fel a kérdést, hogy hol lehet az elektron és ennek mekkora a valószínűsége, hogy egy adott helyen megtalálható. Ez a valószínűség a komplex állapotfüggvényből képezhető, egy olyan matematikai művelettel, ami konvertálja a komplex jelleget és valóssá teszi. Ez a valószínűség azonban nem ismerethiány, hanem az elektron mozgásának objektív képe. Ha úgy tetszik, ez a mikroállapot valósága. Így találkozik ismét a fizikai valóság és a matematikai forma valós jellege! Ez a valószínűség az idő átalakult dimenziója a mikrovilágban, talán jobb lenne nem is valószínűségnek nevezni, hanem tartózkodási eloszlásnak, vagy tartózkodási sűrűségnek.
Pálya és állapot
Hasonlítsuk össze a makrovilág és a mikrovilág megfigyelési módjának három alapszabályát! Induljunk ki megszokott világunkból. Van is először valamilyen objektum, például egy csillag, vagy egy labda, ami megjelölhető, és ennek követjük egymásutáni pillanatokban a pozícióját, feltételezésünk szerint tetszőleges pontossággal, és ez a megfigyelés nem befolyásolja azt, hogyan mozog ez a test. De mi a helyzet például egy elektron esetén? Először is az egyes elektront nem tudjuk megjelölni, ha egy víz molekulára gondolunk, abban 18 elektron van, melynek állapotát együttesen tudjuk leírni, de az egyes elektronnak nincs identitása, nem tudjuk megkülönböztetni ezeket és ezért nem tudjuk megmondani, hogy egy kiszemelt elektron éppen hogyan mozog. Sőt nem is látjuk az elektronokat csak akkor ha „meglökjük”, más pályára kényszerítjük. Vagyis a megfigyelés alapvetően változtatja meg a megfigyeltet. Maga a pálya, amit tehát nem látunk, csak elképzelésünkben létezik, melynek matematikai leírását imaginárius matematikai formában tudjuk megadni, és a mozgást leíró fizikai mennyiségek, mint a lendület és mozgási energia is elképzelt, vagyis imaginárius identitással rendelkezik. Elképzeljük, hogy ha nem hat erő az elektronra, akkor lendülete nem változik meg, és ezt a kérdést fogalmazzuk meg egy imaginárius operátorral, amely egy kérdőszó: a tér koordinátákkal definiált differenciálhányados. A mozgás fő állandója az energia, ez az ami definíció szerint nem változik meg. Ez is egy kérdőszó, az idővel képzett derivált és ott szerepel benne az imaginárius szám, az „i” is. Igy jön harmóniába a matematikai imaginárius forma a fizikai fogalom elképzelt ideájával.
Amikor a mikrovilágban az elektron állapotára kérdezünk, nem azt keressük, hogy hol van pillanatnyilag az elektron, csak azután kutakodunk, hogy hol lehet! A hol lehet kérdésére azt a választ kapjuk, hogy egyidejűleg lehet itt és ott is. Ez teljesen szembe megy a megszokott felfogással, ahol egymásutáni pozíciókra bontjuk fel a pályát, ezért kell térben kiterjedt állapotról beszélni, amelyben a valószínűség adja meg az elektron eloszlását.
Az EPR paradoxon: létezik-e rejtett mozgás a kvantummechanikai valószínűség mögött?
A nagy kérdés, hogy az eloszlás mögött létezik–e egy lefutás, amit ugyan nem látunk, de rejtetten mégis ott van. Ezt tételezte fel Einstein is, amikor a kvantummechanikát kiegészítő rejtett paraméter létezését tételezte fel. Ez indította el a három szerző (Einstein, Podolsky, Rosen) által elindított EPR paradoxon körüli hosszú vitát. Döntő cáfolatot BELL adta meg, aki egy konkrét példával, amit most Bell egyenlőtlenségnek nevezünk, cáfolta meg, hogy kiegészíthető lenne ily módon a kvantummechanika világa. Én más oldalról mutatom meg, hogy ez a klasszikus pálya fogalomra épített koncepció nem fogadható el.
A Hidrogén atom elektronpályái közül válasszuk ki a p pályákat, melynek térbeli eloszlását láthatjuk. Ennek az a jellemzője, hogy van egy sík, ami a pálya két részét szétválasztja. Vagyis az elektron lehet a sík fölött is, meg alatt is, viszont a síkban nem lehet. Ha tényleg mozogna az elektron, akkor hogyan tudna átmenni a sík fölötti tartományból az alattiba úgy, hogy soha sincs magában a síkban.
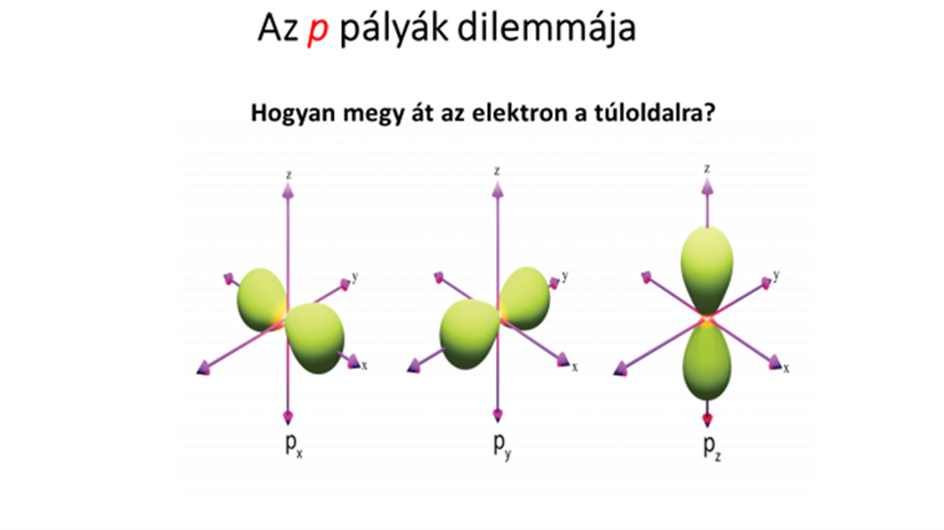
A másik kizáró okot az elektrodinamika törvényei adják. A klasszikus fizika talán legszebb fejezetét az elektrodinamika törvényei szolgáltatják, a Maxwell egyenletek. Ennek egyik következménye, hogy a töltés gyorsulása elektromágneses sugárzással jár együtt. Ez jól megfigyelhető, amikor elektronokat gyorsítunk fel a ciklotronban. Minél intenzívebb a gyorsítás, annál erősebb a kisugárzott fény. Az elektronok viszont csak akkor sugároznak ki fényt a molekulákból, amikor ugrás történik két állapot között. Ha viszont nincs ugrás, akkor nincs sugárzás sem. Ha viszont a stacionárius állapotban valódi keringést végeznének az elektronok, akkor gyorsulnának ennek során. Mi ebből a következtetés? Az elektronok nem gyorsulnak a stacionárius állapotban, vagyis nem végeznek tényleges keringő mozgást, hanem egyszerűen csak ott vannak egyidejűleg egy kiterjedt tartományban! Az eloszlás tehát nem időben történő mozgás következménye!
Az idődimenziót felváltja a valószínűség
A mikrovilág stacionárius állapotában tehát elvész az idő fogalma, de mozgásról mégis beszélhetünk. Ennek oka, hogy belép helyette egy másik fogalom, amit jobb híján valószínűségnek nevezünk. Csak jobb híján, mert itt a valószínőség mozgási dimenzió és nem ismerethiány. A mozgási állapotot jellemző valószínűségi eloszlás egyenértékű a klasszikus mozgási pályával, csak a dimenzió más. Ezt is az időhöz hasonlóan pozitív valós számok írják le, csak a skála megválasztása tér el, mert az idő a „most”-tól számítva bármekkora lehet, míg a valószínűség két határértéke 0, ha valami lehetetlen és 1 a teljes bizonyosságé. De ez csak definíció kérdése, választhatnánk végtelen értéket is a teljes bizonyosság definíciójára. Amíg a pálya leírásban beszélhetünk lassú és gyors mozgásról, ennek helyébe lép az elmosódott és az éles valószínűségi eloszlás. Új értelmet nyer a „lehet” fogalma is, ami nem csupán a valóság előképe, hanem a mikrovilág valósága is. Itt a gondolkodás két szintjéről van szó, ha a makrovilág fogalmi rendszeréből indulunk ki, úgy fogalmazunk, hogy „hol lehet” az elektron, de ha már elsajátítottuk a mikrovilágon alapuló gondolkodást, az mondjuk, hogy „hol van” az elektron, azaz hogyan oszlik el a térben.
Ütközik-e a klasszikus fizika determinisztikus és a kvantummechanika indeterminisztikus felfogása?
Gyakran emlegetik tudományos körökben is, hogy van a modern fizikának egy nagy adóssága, mely szerint a modern fizika két jól bizonyított elmélete nem egyeztethető össze. Azt mondják, hogy amíg a gravitáció elmélete, az általános relativitás determinisztikus alapon áll, addig a kvantummechanika nem determinisztikus. Szerintem ez csupán álvita, ami a determinizmus félreértésén alapul. A bolygók pozíciója és sebessége, azaz lendülete egy adott pillanatban tetszésszerinti pontossággal megadható, szemben az elektron esetével, ahol a Heisenberg határozatlansági elv szerint a két mérés hibájának szorzata elvi korlátba ütközik, mert nem lehet kisebb a Planck állandónál. Most ne menjünk bele abba a kérdésbe, hogy a pozíció és lendület mérésének milyen gyakorlati korlátai vannak, csak nézzük az elvi alapokat. A lendület a klasszikus fizika adekvát paramétere, ami a mozgási pálya meghatározója, ez már nem érvényes a mikrofizikában, az állapot meghatározója már nem a lendület. Ott az adekvát leírást a kvantumszámok adják, ezért a mikrovilág determinizmusa a kvantumszámok meghatározását jelenti. Tehát a mikrovilágban az jelenti a determinizmust, hogy meg tudjuk határozni a kvantumszámokat. A határozatlansági reláció csupán azt jelenti, hogy a lendület nem adekvát fizikai mennyiség. A kvantumszámok adekvát jellege megjelenik a matematikában is, amit az fejez ki, hogy ezek természetes illetve egész számoknak felelnek meg.
Honnan ered a határozatlansági reláció?
Érdemes még néhány szót szólni a határozatlansági reláció eredetéről is. Ez onnan származik, hogy a mikrovilág hírhozója a fény, a foton. A fotonhoz tartozik egy hullámhossz is, ennek nagysága határozza meg, hogy milyen pontos információt kapunk onnan, ahonnan a foton megérkezik. De nem csak a pozíciót, hanem a lendületet is a foton segítségével határozzuk meg, itt a pontossági határt a foton lendülete határozza meg. Viszont foton esetén a hullámhossz és a lendület szorzata a Planck állandó. Ha pontos pozíciót akarunk mérni, akkor rövid hullámhosszra van szükségünk Például a látható fény hullámhossza több nagyságrenddel nagyobb a kristályokban a rácstávolságnál, ezért a nagyobb energiájú röntgensugarakat kell alkalmazni, hogy feltárhassuk a molekulaméreteket. Ez viszont nagy lökést ad a molekulának, ami megváltoztatja az eredeti lendületet, és így pontatlanná teszi annak mérését.
Ez a határozatlansági elv matematikailag a fizikai mennyiségek operátorainak nem kommutatív jellegében tükröződik.
A mikrovilág determinizmusa és a kvantumszámok
A mérés megváltoztatja ugyan a kvantumszámot is, de azt pontosan meg tudjuk mondani, hogy mekkora a kiinduló és a megváltozott kvantumszám. Elvben a makroszkopikus objektum kvantumszám kombinációja is megadható lenne, de a hatalmas számú elektron miatt ez egy lehetetlen vállalkozás. De erre nincs szükség, mert a nagy részecske szám miatt a kvantummechanika bizonytalansági elve elhanyagolható válik és a korrespondencia elv szerint a mechanika törvényei átmennek a determinisztikus klasszikus mechanika törvényeibe. Emiatt csak álproblémának tartom a gravitációs törvények szembeállítását a kvantummechanikával.
Valójában a mikrovilág törvényei is determinisztikusak, amit a kvantumszámok jól definiált és egyértelmű értékei fejeznek ki. A határozatlansági reláció azt mutatja meg, hogy a makrovilágból átvett fogalmak, mint a pozíció és a lendület, nem adekvát mennyiségek a mikrovilágban.
A mozgási állapotok identitása
A kvantumszámokkal jellemzett állapotfüggvény az elektron mozgási állapotának identitását fejezi ki. Az identitás megköveteli, hogy az egyes állapotok teljes mértékben elkülönüljenek, amit matematikailag az egész térre kivetített integrál adja meg. Az egyes pontokban a komplex függvény komplex konjugáltja adja meg a pozitív lokális valószínűséget, amit integrálva (összegezve) az egész térre kapjuk meg az egységnyi valószínűséget, azaz, hogy a kiszemelt elemi objektum bizonyossággal létezik. Az identitáshoz az is hozzá tartozik, hogy két különböző állapot között nincs átfedés, vagyis az egész térre számított integrál a két állapotfüggvény szorzatára nulla lesz (pontosabban az egyik függvény komplex konjugáltját szorozzuk a másik függvénnyel). Erre csak komplex függvény lehet képes, mert a pusztán pozitív valószínűségi eloszlások szorzata mindenhol pozitív lesz. Az állapotfüggvény komplex jellege azt is szimbolizálja, hogy a valóság és a róla alkotott képzetünk egymásba fonódva jelenik meg a mikrovilágban. A teljes világ a megfigyelhető és az elképzelt világ együttese, melynek leírását szolgálja a komplex állapotfüggvény, melyben ott van a valós és imaginárius rész is, utalva arra, hogy a kettő együtt teszi ki az egészet.
Az idő megjelenése a mikrovilág irányából
Fordítsuk meg túránk irányát és most a mikrovilág felől közelítsünk a makrovilág felé. Hogyan lesz ekkor a valószínűségből idő? Ezt az elemi objektumok nagy száma biztosítja. A klasszikus mechanikában a periodikus mozgások segítenek, hogy skálázzuk az időt, azaz megalkossuk az órát. A periodikus mozgások mechanikája mögött húzódik meg, hogy nagyszámú objektum esetén a kvantummechanika valószínűségi törvényei határesetben a klasszikus törvényeket adják ki.
Az idő belépését a radioaktív izotópok belső órájával értelmezhetjük, ami minden egyes izotóp számára azonos bomlási valószínűséget ad meg. Az egyes izotópokat nem láthatjuk, mert ha látnánk, az egyúttal annak megváltozását jelentené, vizsgálhatjuk azonban az izotópok sokaságát. Mennyi fényt, például gamma sugarat, vagy elektront bocsátanak ki a bomlási folyamatban. Mivel az az izotópok anyagában az egyes részecskék nem különböztethetők meg, így a részecskeszám határozza meg a bomlási gyakoriságot, ami a változás mértékét határozza meg. Megadhatjuk így a felezési időt, ami alkalmassá teszi az izotópokat a kormeghatározásra.
A mikrovilág szótára
Összefoglalásként elkészítettem egy kis szótárt, amiben lefordítom a makrovilág fogalmait a mikro világéra. Kiindulópont a pálya, melynek helyébe az állapot lép. Az idő leváltója a valószínűség, de ezt is másképp értelmezzük a mikrovilágban, itt már jobb helyette tartózkodási eloszlást mondani. Amikor a makrovilág fogalmait használjuk a mikrovilág mozgásainak leírására, akkor tesszük fel a kérdést, hogy az elektron hol lehet. De ha sikerül továbblépni és már a mikrovilág fogalmaiban gondolkodunk, már az lesz a helyes kérdés, hogy hol van az elektron, azaz mekkora súllyal tartózkodik az elektron a tér különböző tartományaiban. A világ egysége is megjelenik a kvantummechanikában. Az elektron tartózkodási súlya az atomban a magtól bármekkora távolságban is megjelenik, bár ez a súly a Gauss eloszlást követve csak az atom belsejében jelentős, de azért mindenütt ott van. Ebben az értelemben a világ összes elektronja egyetlen nagy egységet alkot. Bármely két elektront kiválasztva van közöttük „párbeszéd”.
Érdekes, hogy mi történik a sebesség fogalmával. Ezt már a térbeli eloszlás élessége helyettesíti. Ebből fakad a gyorsulás fogalma is, ami a geometriai alakzat élesedését jelenti, vagy lassuláskor elmosódottságot, szélesedést jelent. A legizgalmasabb a határsebesség, a c értelmezése, mert ez hozzásegít, hogy jobban értsük a határsebesség eredetét. Ez onnan származik, hogy a pontszerűség jelenti felbontási határt a mikrovilágban, ennél jobb felbontás, élesebb eloszlás nem lehet. Ennek megfelelőjeként mondhatjuk, hogy van egy sebesség, ami nem léphető át a makrovilágban. Így segít a mikrovilágról alkotott képünk jobban megérteni a relativitáselméletet is.

 Ez vezet el a spin, a perdület fogalmához. A fermionok tömege a lokális gömbforgások ω frekvenciájától függ: minél nagyobb a forgás frekvenciája, annál nagyobb a tehetetlenség. Az ω frekvencia egyúttal kijelöli a forgó objektum méretét is az ωr = c szabály miatt. A relativitáselmélet azáltal kerüli el a szingularitást, hogy a sebességfüggő tömegnövekedési törvény megtiltja, hogy a tehetetlenséggel (tömeggel) rendelkező objektumok fénysebességgel haladjanak. A tömegnövekedési törvényt terjesszük ki határértékben nulla tömegre is:
Ez vezet el a spin, a perdület fogalmához. A fermionok tömege a lokális gömbforgások ω frekvenciájától függ: minél nagyobb a forgás frekvenciája, annál nagyobb a tehetetlenség. Az ω frekvencia egyúttal kijelöli a forgó objektum méretét is az ωr = c szabály miatt. A relativitáselmélet azáltal kerüli el a szingularitást, hogy a sebességfüggő tömegnövekedési törvény megtiltja, hogy a tehetetlenséggel (tömeggel) rendelkező objektumok fénysebességgel haladjanak. A tömegnövekedési törvényt terjesszük ki határértékben nulla tömegre is:
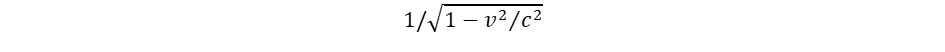 tömegnövekedéssel szorozzuk, ami már véges értéket adhat. A végesség az anyagi világ jellemzője, az anyag létformája. A tömegmentes tér csak matematikai fikció. Valamennyi bozont és fermiont fénysebességű forgás alkot, melyek a mozgások szimmetriájában és a forgások dimenziójában (egydimenziós, tengely és kétdimenziós, gömbforgás) különböznek.
tömegnövekedéssel szorozzuk, ami már véges értéket adhat. A végesség az anyagi világ jellemzője, az anyag létformája. A tömegmentes tér csak matematikai fikció. Valamennyi bozont és fermiont fénysebességű forgás alkot, melyek a mozgások szimmetriájában és a forgások dimenziójában (egydimenziós, tengely és kétdimenziós, gömbforgás) különböznek.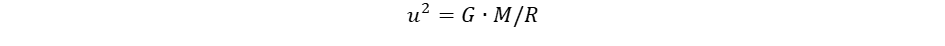 (2)
(2)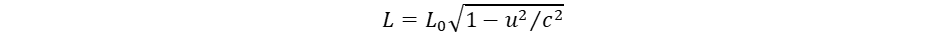 (3)
(3) (4)
(4)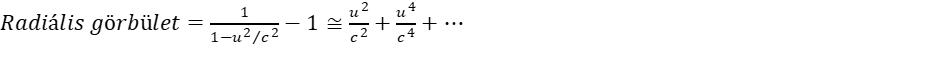 (5)
(5)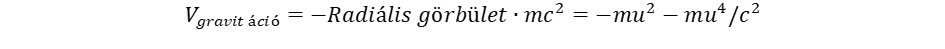 (6)
(6)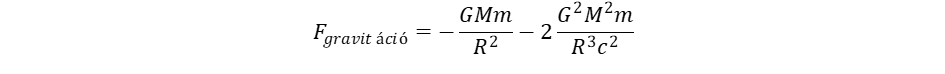 (7)
(7) (8)
(8)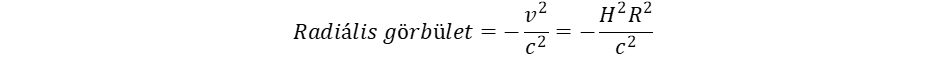 (9)
(9)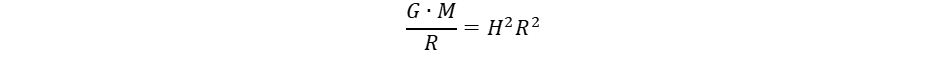 (10)
(10)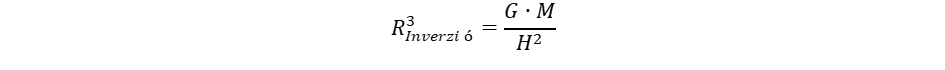 (11)
(11)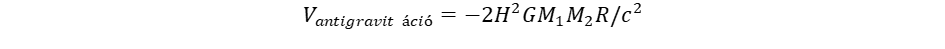 (12)
(12) (13)
(13)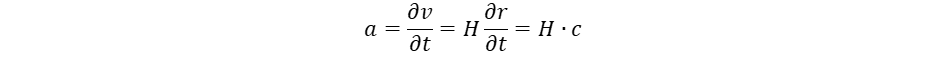 (14)
(14)
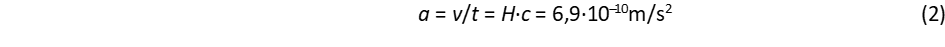
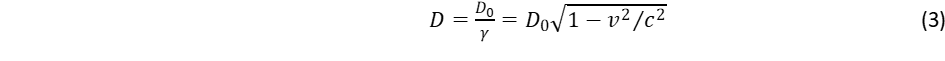
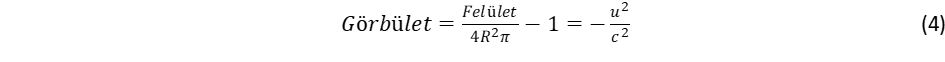
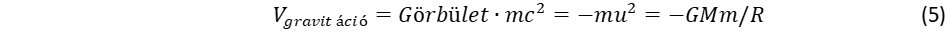
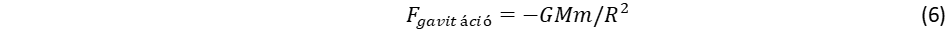
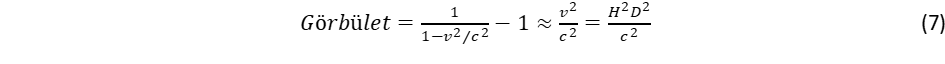



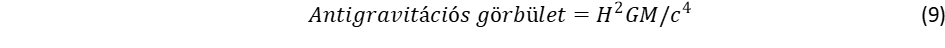
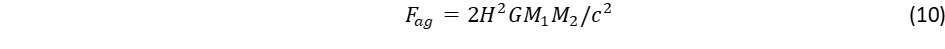

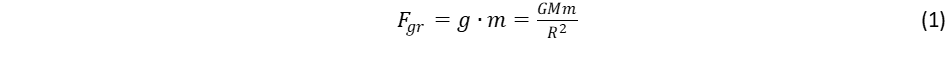

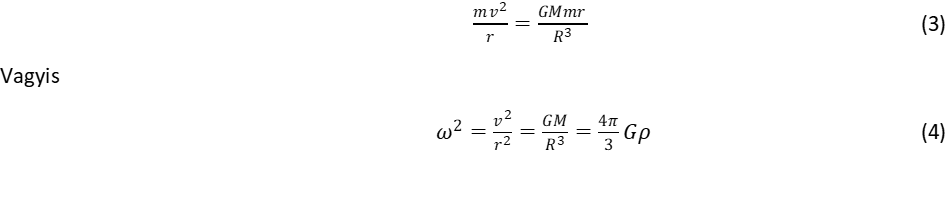

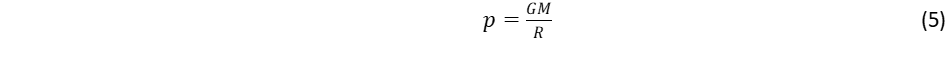

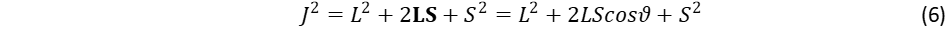
 (1)
(1)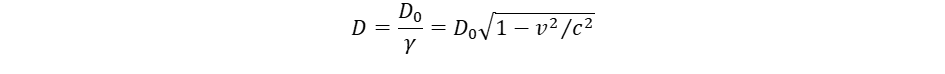 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) ___________________________________________________________________________________
___________________________________________________________________________________ (8)
(8) (9)
(9) (10)
(10) (11)
(11)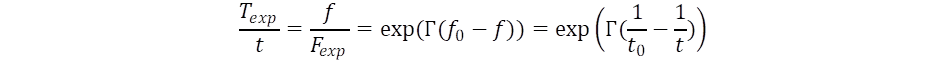

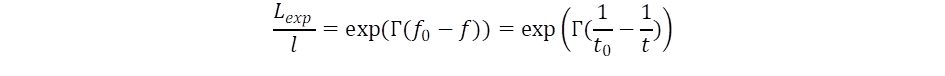
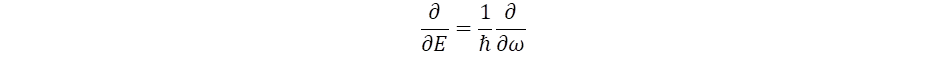 differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva:
differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva: