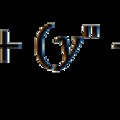Az előző írás: A fénysebesség csökkenés mechanizmusa és a kvantum fluktuáció

Linkek a korábbi bejegyzésekhez

Távolhatások és kontakt kölcsönhatások

A Föld és a többi bolygó a Nap körül kering, a pályát a távoli égitestek közötti láthatatlan gravitációs erő hozza létre. Nincsenek a testek összekötve, ezért közöttük távolhatásról beszélhetünk. Az atommag körüli pályákon elektronok mozognak, ennek létrehozója a pozitív töltésű atommag és a negatív elektronok közötti elektromos vonzóerő. Bár itt a távolságok parányiak, mégis távolhatásról beszélhetünk, mert nincs látható kapocs a részecskék között. Ez a távolhatási kép volt uralkodó, amikor kialakult a kvantummechanika, és magyarázatot adott az atomok és molekulák szerkezetére. Később születtek meg a mezőelméletek, elsőként a kvantumelektrodinamika, amely alapvető változást hozott a fizikai szemléletben, előtérbe került a koncepció, hogy a távolhatás mögött kontakt mechanizmusok állnak, melyekben virtuális fotonok hozzák létre az elektromágneses vonzó és taszító erőt. A virtualitás azt jelenti, hogy ezek a fotonok közvetlenül nem figyelhetők meg.

Megfigyelhető és virtuális fotonok, a vákuum fluktuáció

A fény természetére először a Maxwell egyenletek megszületése adott magyarázatot, vákuumban is áramlanak elektromágneses hullámok, melyek képesek erőt gyakorolni, ha oda elektromos töltést helyezünk. Planck felismerése volt, hogy a fény is egyedi objektumokból áll, a fotonokból. A foton olyan fénysebességgel (c), haladó hullám, amelynek minden periódusára ugyanakkora lökő erő tartozik, és minden periódusának ugyanakkora az energiája, ezt fejezi ki, hogy a teljes hullám impulzusa a távolság egységre jutó hullámszám (p = h/λ), és energiája az időegységre jutó periódusok száma: E = hf. Itt h a Planck állandó, a téridő univerzális tulajdonsága a c fénysebesség mellett, ez a kvantum egysége is, amit gyakran a ħ = h/2π redukált Planck állandóval is jelölünk. A foton voltaképp két töltés kölcsönhatása a térben. Valahol a térben egy elektron állapota megváltozik, például a lámpa izzószálában, vagy a Napban, ezáltal útjára indít egy fotont, amely eljut valahol egy másik elektronokhoz, legyen az akár közel, de lehet fényévnyi távolságra is. Az „utazó” foton hatására megváltozik ennek a másik elektronnak az állapota. Ezen az állapotváltozáson alapul minden megfigyelés és a látásunk is.

E történet idáig a megfigyelhető valódi fotonokról szólt. A virtuális fotonoknak más a szerepük, nem az elektronok állapotát változtatják meg, hanem fenntartják, létrehozzák a töltések között ható erőt. Ennek eszköze a fotonok impulzusa, amely meglöki a töltéssel rendelkező részecskéket, így az elektronokat is. Minden töltéssel rendelkező elemi objektum, legyen szó elektronokról, vagy az atommagok protonjairól, állandóan kibocsát és elnyel virtuális fotonokat. A mechanizmusra szemléletes magyarázatot kínál a fénysebességű forgások koncepciója, melyben kettősforgások alkotják a részecskéket, összefoglaló néven a fermionokat. A részecske sajátforgásának centrifugális erejét a fénysebességű forgás által előidézett extrém térgörbület gravitációs ereje egyenlíti ki. Ez a magyarázat az általános relativitáselméletre támaszkodik. A két forgás között fellép egy további tehetetlenségi erő, a periodikusan változó Coriolis erő, amelynek átlaga nulla. Ennek az erőnek körüljárási irányát a két forgás királis szimmetriája szabja meg. A Coriolis erő periodikusan megtöri a forgást fenntartó erőegyensúlyt, a periódus egyik fázisában a kifelé ható erő lesz nagyobb, ekkor kerül sor az egytengelyű forgás, azaz a foton kibocsátására. A periódus másik felében a befelé húzó erő lesz a domináns, ekkor nyeli vissza a részecske a virtuális fotonokat. Kibocsátáskor a foton impulzusát az elektron biztosítja, amely ekkor a fotonéval ellentétes irányban lökődik meg, ezáltal téve eleget az impulzus megmaradásának. Elnyeléskor az elektron visszaveszi az impulzust, azaz fordított irányú elmozdulás következik be. A két folyamat összjátéka állandó fluktuációt okoz az elektron pozíciójában. Ezt nevezi a szakirodalom vákuum, vagy kvantumfluktuációnak, és ennek segítségével lehet magyarázni, hogy miért nagyobb az elektron mágneses nyomatéka, mint ami a relativisztikus Dirac egyenletből következik.

Vonzás, taszítás és a fotonok polaritása

De miért jön létre taszító erő két elektron között, és miért vonzás a pozitív töltésű atommag és a negatív elektronok között? A virtuális fotonok kibocsátása és elnyelése dinamikus egyensúlyt hoz létre, amit úgy foghatunk fel, hogy a részecskét kiegészíti egy virtuális foton felhő, amely létrehozza az elektromágneses kölcsönhatást. Ez a felhő képviseli az elektron mc² energiájának egy kis hányadát, amit. a Sommerfeld féle α = 1/137 állandó mond meg, a szakirodalomban ezt nevezik finom-kölcsönhatási állandónak. Ez határozza meg az elemi töltés nagyságát is az e² = αħc összefüggésben (e a töltés). A töltés előjelét viszont az határozza meg, hogy milyen a kettősforgás kiralitása, ami: jobb, vagy a balkéz szimmetriájú lehet. Például negatív töltéshez rendelhetjük a jobbkéz, a pozitívhoz a balkéz szimmetriát. Persze a választás önkényes, lehet fordítva is. A jobbkéz szimmetria esetén jobbsodrású, balkéz szimmetriánál balsodrásúak lesznek a kibocsátott fotonok a Coriolis erőnek megfelelően. Amikor két elektron kölcsönhatásba kerül mindkettő jobbsodrású fotonokkal van körülvéve, de mivel a másik elektrontól érkező fotonok terjedési iránya az elsőhöz képest fordított, a kölcsönhatás létrejöttekor a „befogadó” elektron oldaláról nézve megfordul a forgás sodrásiránya, azaz balsodrású lesz. A virtuális fotonok szuperponálódnak az átfedési tartományban, és az ellentétes polaritások kioltják egymást. Emiatt a két elektron közötti tartományban lecsökken az elnyelhető fotonok sűrűsége. A kibocsátás és elnyelés egyensúlya megbomlik, hiszen a foton kibocsátások gyakorisága változatlan marad, amiért összességében a taszító hatás fog dominálni, vagyis taszítják egymást az elektronok. Megfordul a kép a negatív és pozitív töltések kölcsönhatásakor. Ekkor a pozitív töltésű részecske balsodrású foton felhője a negatív töltés számára jobbsodrásúként viselkedik. Ez a két részecske közötti tartományban megnöveli a foton sűrűséget, amiért nagyobb lesz az elnyelések sebessége a kibocsátáshoz képest. Ez pedig már vonzást hoz létre a felborított impulzus mérleg miatt.

 A foton felhők sűrűsége a távolság négyzetével csökken, emiatt a vonzó, vagy taszító erő is ebben az ütemben változik, ami megfelel a Coulomb törvénynek, amely szerint F_Coulomb = q₁q₂/r², ahol r a q₁ és q₂ töltések távolsága. A q₁ töltés erőkifejtési képességét leírhatjuk az E₁ = q₁/r² elektromos mező fogalmának bevezetésével is, amikor is F_Coulomb = E₁q₂.

Mágneses mező: a Coulomb kölcsönhatást kiegészítő retardációs hatás

Mozgó töltések esetén az erőhatás megváltozik, mert idő kell a virtuális fotonok áramlásához is, ezt pedig a c fénysebesség határozza meg. A fotonok érkezési ideje r távolság esetén Δt = r/c, ez alatt a v sebességű részecske eredeti helyéhez képest vr/c utat tesz meg. A töltések közötti erőhatás nagyságát és irányát ezért nem az határozza meg, hogy pillanatnyilag mekkora az r távolságuk, hanem az, hogy mekkora volt Δt idővel korábban (retardáció). Ha a mozgás nem az összekötő r vektor irányában történik, akkor fellép az r és v vektorokra egyaránt merőleges erő, ezt írja le a B mágneses mező segítségével a Lorentz formula:

F_Lorentz = q(E +vxB)

Ezt felfoghatjuk a B mágneses mező definíciójának, amely megmondja, hogy a hatás késlekedése (retardáció) miatt, hogyan kell korrigálni a töltések közötti erőhatást. A mágneses kölcsönhatás a Coulomb erőt kiegészítő relativisztikus járulék, amely azonban nem a vektor felbontásnak megfelelő v irányába mutat, hanem arra merőleges. Ennek oka, hogy amíg a Coulomb erőt a virtuális fotonok impulzusa hozza létre, addig a mágneses kölcsönhatás a fotonok impulzusnyomatékához kapcsolódik, amely pedig merőleges az impulzusra. Másként fogalmazva, arról van szó, hogy mozgó töltések esetén a foton felhők terjedési iránya szöget zár be egymással, ami merőleges irányban is létrehoz egy erőhatást.

Korábbi írásunkban részletesen foglalkoztunk avval a kérdéssel, hogyan hoz létre a fénysebességű forgás mágneses nyomatékot, amely arányos a töltéssel és a Compton sugárral. Az anomális mágneses nyomatékot a kvantum fluktuációk által megnövelt sugárral lehetett értelmezni. Ez a növekedés úgy is szemléltethető, hogy az elektron virtuális foton felhője megnöveli a részecske effektív sugarát.

Az s elektronok különös viselkedése: a Lamb shift

Az előző írásban már utaltunk rá, hogy a kvantum fluktuáció miatt bizonyos energiaállapotok degenerációja megszűnik, amit Lamb és Retherford meg is figyelt a Hidrogén atom két állapota között. Az energianívókat a Schrödinger egyenlet szerint az n fő kvantumszám határozza meg, de a relativisztikus Dirac egyenlet szerint ezek a nívók felbomlanak az L mellék kvantumszám szerint, ezt nevezik finom-kölcsönhatásnak, melynek mértéke a már említett α állandóval jellemezhető. Az L kvantumszám határozza meg az elektron Lħ pálya impulzusnyomatékát. Az L kvantumszám n-1-nél nem nagyobb egész értékeket vehet fel. Az alapállapot 1s_1/2, az első három gerjesztett állapot 2s_1/2, 2p_1/2 és 2p_3/2. Itt az elő szám az n fő kvantumszám, az s és p azt jelöli, hogy L = 0, vagy L = 1. Az S = ½  spin és L csatolódik, kiadva az eredő impulzusnyomaték kvantumszámot, ami ½ vagy 3/2 lehet, ezt jelöli az alsó index. Megfelelő frekvenciájú elektromágneses sugárzással az 1s_1/2 alapállapot gerjeszthető a 2p_1/2 állapotba, mert ekkor a foton ħ impulzusnyomatéka viszi át az elektront a magasabb impulzusnyomatékú L = 1 állapotba. A hőmérséklet függvényében bizonyos számban a Hidrogén atom magasabb energiájú állapotai is betöltésre kerülnek, ezért felmerül a kérdés, hogy lehetséges-e a részlegesen betöltött 2s_1/2 és 2p_1/2 állapotok között is átmenetet létrehozni elektromágneses sugárzással. Ennek ellentmondani látszik, hogy a két állapot energiája a Dirac egyenlet szerint megegyezik.

 Viszont Lamb és Retherford kimutatta, hogy a szokásos optikai átmeneteknél sokkal kisebb frekvenciájú (1057 MHz) mikrohullámmal mégis indukálható átmenet, azaz a két állapot energiája ennek mértékében különbözik.  Ennek oka, hogy a –e²/r² Coulomb erő r = 0 szingularitása feloldódik a kvantumfluktuáció miatt. A Schrödinger és a Dirac egyenlet egyaránt megengedi, hogy az elektron véges valószínűséggel ott lehessen az atommagban is, ahol r = 0. Az energiaszámításban integrálni kell a teljes tértartományra, melynek során az egyes tartományokban való tartózkodás valószínűségét szorozni kell az ott érvényes potenciális energiával. Az r = 0 határeset közelében a valószínűség arányos a térfogattal, azaz 4r³π/3-mal, ezért összességében az innen származó járulék az r sugárral lesz arányos, azaz határértékben nullához tart. Az s és p pályák között fontos különbség, hogy az s pályáknak nullától különbözik a valószínűségi sűrűsége a magban, szemben a p pályákkal, amely ott nullasűrűségű. Ennek oka, hogy nulla impulzusnyomaték zárt pályán csak úgy jöhet létre, ha a mozgási irány áthalad a centrumon. Viszont a p pályák nullától különböző impulzusnyomatéka miatt a mozgó elektron nem juthat oda. Az energia integrál mégis megegyezik a 2s_1/2 és 2p_1/2 pályák esetén, tehát az s pálya mag helyén számított potenciális energiajárulékát a p pálya más tartományai kiegyenlítik. A fluktuációs hatás döntően a mag helyén csökkenti a negatív potenciális energiát, míg onnan távolabb kisebb a szerepe. Az s és p pályák vonatkozásában ez azt jelenti, hogy az eredetileg degenerált pályák közül a 2s_1/2 pálya energiája lesz nagyobb.

A Lamb shift számításánál abból indulhatunk ki, hogy a V(r) potenciális energia hogyan változik, ha az r vektorhoz hozzáadunk egy kis δr értéket. A sorfejtési eljárásban δr különböző hatványait kapjuk, amelyben a magasabb hatványok már elhanyagolható járulékot adnak. A számításnál célszerű a  differenciál vektort alkalmazni. A potenciális energia változása:

A potenciális energia változásának várhatóértékét az elektron ψ(r) állapotfüggvényét tartalmazó integrál adja meg. A fluktuáció minden irányban egyformán valószínű, ezért az integráláskor az első tag eltűnik. A második négyzetes tagban a három ekvivalens irány miatt belép egy 1/3-as faktor, amiért a várhatóérték:

 Az 1/r szerint változó potenciális energia  operátorral képzett deriváltja a szinguláris r = 0 pontban ugyan végtelen, de a teljes térre vett integrál véges lesz, és arányos az állapotfüggvény négyzetének nullaponti értékével:

Ez azt jelenti, hogy az állapotfüggvénynek a potenciális energia szingularitás pontján vett értéke – más szóval a centrum állapotsűrűsége – határozza meg, hogy a fluktuáció mennyivel növeli meg a potenciális energiát. A 2s pálya állapotsűrűsége a centrumban:

Itt a₀ a Bohr sugár. Hidrogén atomban a potenciális energia V(r) = -e²/r, amiért a fluktuációs energianövekmény:

Az elektronpályák kiterjedését jellemző Bohr sugár viszonyát a fénysebességű forgások R_c = ħ/mc Compton sugárhoz képest az α = 1/137 Sommerfeld állandó reciproka határozza meg, ez az állandó, amely kifejezi az elemi töltés nagyságát is az e² = αħc összefüggésben

a₀ = ħ²/me² = ħ/αmc = R_c/α

A korábbi részben tárgyaltuk az elektron anomális mágneses nyomatékának kérdését, amit az A_flu = αR_c fluktuációs amplitúdóval lehetett értelmezni. (Ez a fluktuációs amplitúdó azonos a klasszikus elektronsugárral, amelyet úgy definiálnak, hogy a Coulomb energia egyezzen az mc² nyugalmi energiával). A potenciális energia növekményében szereplő fluktuációs kitérés ennél nagyobb, mert nem arról van szó, hogy a virtuális fotonok kilépése mekkora fluktuációt okoz a mágneses mezőben forgó elektron pozíciójában, hanem arról, hogy a pályamozgás során a centrum felé haladó mozgást milyen mértékben téríti ki a virtuális fotonok kibocsátása és elnyelése az atommag pozíciójához érve. Az egzakt számítást a kvantumelektrodinamika végzi el, itt ehelyett a fluktuációs kitérés δr paraméterét igazítjuk a kísérletileg mért 1057 MHz shift nagyságához, mely szerint:

δr = 0,7338·10^-13 m

Ez a kitérési amplitúdó 0,19-szer kisebb a Compton sugárnál, de 26-szor nagyobb, mint a fluktuációs amplitúdó. A kitérési amplitúdó nem univerzális állandója az elektronnak, hanem a Hidrogén 2s pályára érvényes. Más pályákon eltérhet az értéke, például a kompaktabb 1s pályán ennél kisebb lehet.

A s elektron különös viselkedése: a Fermi kontakt kölcsönhatás

Az atommagon áthaladó s elektronok másik közvetlen hatása, hogy emiatt az elektron mágneses nyomatéka közvetlen kölcsönhatásba kerül az atommag mágneses nyomatékával. Az elektron mágneses nyomatékáról az előző bejegyzésben volt szó. A nyomaték egysége elektron esetén a Bohr magneton:

μ_el = eħ/2m = ecR_c/2

amelyet az elektron S spinjével és a g_e = 2,0023 faktorral szorozva kapjuk meg a nyomaték operátorát. A fénysebességű forgások modelljében ez az R_c sugarú köráramra vezethető vissza.

Az elektronspin rezonancia (ESR) kísérletekben külső B mágneses mezőbe helyezünk olyan elektronokat, melyek spinjét nem kompenzálja a kémiai kötés. Ez paramágneses vegyületekben valósul meg. Az ilyen anyagoknak két alaptípusa van: a szabad gyökök és az átmeneti-, illetve ritkafémek vegyületek. Az előbbiekben a vegyérték héjakban párosítatlan elektronok vannak, az utóbbiakban a belső d és f héjak elektronjai csatolódnak úgy, hogy nem jön létre spin kompenzáció. Ekkor az elektronok energiája két nívóra hasad, melyek között f frekvenciájú mikrohullámú térrel besugározva rezonancia átmeneteket hozhatunk létre:

h·f = g_eμ_BB

A rezonancia frekvencia voltaképp a forgást végző mágneses nyomaték Larmor frekvenciája. Megmérve az f és B paramétereket megkapjuk a mágneses nyomatékot. A legegyszerűbb szabad gyök a Hidrogén atom, melyben az atommagot egyetlen proton alkotja. Mivel a proton spinje I = ½, így az elektronhoz hasonlóan szintén rendelkezik mágneses dipólussal, melynek nagyságát mag magneton egységben adhatjuk meg

μ_N = eħ/2m_p

Ezt a g_p = 5,586 faktorral és az I spinnel szorozva kapjuk meg a nyomaték operátort. Alkalmazva B mágneses mezőt az atommagokkal is rezonanciát figyelhetünk meg, ez a mag mágneses rezonancia (NMR) spektroszkópia, amely módot ad az atommagok, például a protonok mágneses nyomatékának mérésére is. Mivel a mágneses nyomaték fordítva arányos a részecske tömegével, ezért a magok mágneses nyomatéka legalább három nagyságrenddel kisebb az elektronhoz képest.

 A mágneses dipólus az iránytól és távolságtól függő mágneses mezőt hoz létre a részecske körül

B_dipol = 3(μ_p·r)r/r⁵ – μ_p/r³

Az ESR kísérletben ez a belső tér módosítja a külső B mágneses mezőt, és felbontja két vonalra a rezonanciát, ez a hiperfinom szerkezet, melynek nagyságát a dipólus mágneses mezőjének várható értéke adja meg a paramágneses vegyület alapállapotában. Amikor az elektron alapállapota p pálya, létrejön az irányfüggő belső mágneses mező, viszont eltűnik gömbszimmetrikus s pályákon, emiatt a Hidrogén atom 1s pályáján nem várnánk hiperfinom felhasadást. Mégis megjelenik hiperfinom szerkezet, de ekkor a felhasadás nem függ az iránytól, azaz izotrop struktúra jön létre. Ezt írja le a Fermi-féle kontakt kölcsönhatás. A jelenség magyarázata, hogy az s elektron nullától különböző sűrűséggel van jelen a mag belsejében, ahol a dipólus mágneses mezője szinguláris. A szingularitás szintje 1/r³ hatványú, az integrálásnál ezt kell szorozni a mag körüli tartományban az r³-al arányos tartózkodási valószínűséggel, így a kölcsönhatás várható értéke véges marad. De honnan származik ez az irány független kölcsönhatás? Ez származtatható a Dirac egyenletből, de hasonló eredményre juthatunk a klasszikus elektrodinamika segítségével is.

Tekintsük a részecskét a fénysebességű forgások elvének megfelelően véges ’a’ sugarú forgó gömbnek, melynek felületén a töltés egyenletesen oszlik el, ekkor az elektrodinamika szabályai szerint mindenütt azonos lesz a forgó töltések által keltett mágneses indukció a gömb belsejében, függetlenül a forgási tengely irányától:

B_belső = 2μ_n/a³

A gömbön kívül továbbra is a dipólus szabály érvényes, amelyben a mágneses mező várható értéke nulla az s pálya szimmetriája miatt. Az ’a’ sugarú gömb belsejében az állapotsűrűség változása elhanyagolható, és azonos lesz a Hidrogén 1s pályájának centrumban felvett értékével:.

Az integrálásnál ezt szorozni kell a 4a³π/3 térfogattal, míg a gömbön kívüli tartomány nulla járulékot ad. Felhasználva az elektron és a proton μ_e = g_eμ_BS, illetve μ_p = g_pμ_NI operátorát, jutunk el a kölcsönhatás nagyságát leíró Fermi operátorához:

Az energia operátornak ez az alakja pontosan megegyezik avval, amit perturbáció számítással a Dirac egyenletből is kaphatunk, és jól reprodukálja a Hidrogén atom ESR spektrumában a protontól származó 1424 MHz frekvenciájú hiperfinom felhasadást.

A Fermi kontakt tag mérése nem ad felvilágosítást arról, hogy mekkora a számításban feltételezett gömb ’a’ sugara, mert ez kiesik a számításból. A fénysebességű forgás modellben ezt azonosíthatjuk az elektron Compton sugarával, amely 137-szer kisebb az a₀ Bohr sugárnál, melyet egyébként a fenti összefüggés alapján kiolvashatunk a proton hiperfinom felhasadásából. Felvethető még, hogy nem kerülhet-e kívülre a proton az elektron belsejéből a centrumtól kitérítő fluktuációk miatt. Mivel a Lamb shift alapján számítva a centrumtól való kitérés mértéke több mint ötször kisebb a Compton sugárnál, ez a lehetőség kizárható. Igaz ugyan, hogy a Lamb shift a 2s pályától származik, de a tényleges kitérés ennél csak kisebb lehet, hiszen a belső pálya kompaktabb. Szokás a Fermi kontakt kölcsönhatást úgy értelmezni, mint ami a proton belsejébe jutó elektrontól származik. Ez a felfogás onnan származik, hogy a nagyobb tömeg miatt a magot nagyobbnak képzeljük az elektronnál. Ennek azonban az ellenkezője igaz, hiszen a mágneses nyomatékból számolható Compton sugár az elektronnál jóval nagyobb. Mivel a proton sugár 0,865·10^-15m, azaz jóval kisebb az elektron Compton sugaránál (386·10^-15 m), így helyesebb az a felfogás, hogy a kontakt kölcsönhatás létrehozásakor a proton helyezkedik el a több nagyságrenddel nagyobb kiterjedésű elektron belsejében. Ennek az sem mond ellent, hogy a pozitronnal való bombázási kísérletben az elektron hatáskeresztmetszete nulla, mert ennek oka, hogy ilyenkor a fénysebességgel forgó objektumot kívülről tanulmányozzuk, amiért a felület nullának adódik a Lorentz kontrakció miatt. A mágneses mérésben viszont a proton belülről „látja” az elektront alkotó forgás gömbfelületét.

A gyenge kölcsönhatás kettősarca: távolhatás és kontakthatás

A két nukleáris kölcsönhatás közül a gluonok által közvetített erős kölcsönhatás a közvetlen kontaktusban lévő kvarkokat kettesével és hármasával összeragasztja a mezonokban és barionokban, úgy szintén az atommagokban ez a kölcsönhatás kapcsolja össze a protonokat és neutronokat. Ez a kölcsönhatás rövid távú, távoli kvarkok és nukleonok esetén nem játszik szerepet. A gyenge kölcsönhatás viszont már kettős arcát mutatja felénk. Ez a kölcsönhatás nem jön létre két fermion (S = ½ spinű részecske) között, hanem az egyes fermionokat alakítja át. Az elemi részecskék közötti minden reakció megköveteli az impulzusnyomaték változatlanságát, ami a spinekre vonatkozólag az ½ + ½ = 1 szabálynak felel meg. Emiatt csak úgy alakulhat át az S = ½ spinű fermion egy másikba, hogy az S = 1 spinű bozon (gyönge kölcsönhatásnál a W és Z bozon) mellett egy további fermion – nevezetesen a neutrínó – is szerepet kap. A gyönge kölcsönhatásnak ezért két közvetítője van. A W és Z bozonok élettartama és hatótávolsága rendkívül rövid, de ez elegendő a „helyben történő”, azaz kontakt átalakításához. Ilyen átalakítás a bétabomlás, amikor egy neutron átalakul egy protonná elektron és neutrínó kibocsátása mellett  A kvark elmélet ezt úgy írja le, hogy a neutront alkotó egyik d kvark (-1/3e töltés) alakul át u kvarkká (2/3e töltés). Az átalakulás első lépcsőjében egy W^- bozon (-e töltés) és egy proton lép ki, majd a W^- bomlik fel egy elektronra és egy neutrínóra. A neutrínóra azonban új szerep vár, ha ütközik valamekkora távolságban egy protonnal, ez gyenge kölcsönhatás révén kiváltja egy W⁺ bozon kilépését, és létrejön egy neutron. A következő lépésben a W⁺ szétválik egy pozitronra és egy neutrínóra. A kvark elmélet szerint a proton egyik u kvarkja alakul át egy –1/3e töltésű d kvarkba. A „két fermion plusz egy bozon” szabály minden lépésben teljesül. Ez már távoli kölcsönhatás két nukleon között, amelynek közvetítője a neutrínó. A neutrínó által közvetített folyamat analógiába hozható a foton szerepével: ott két távoli elektron állapotváltozását közvetíti, hasonló történik a bétabomlásban, ahol két távoli nukleon kvark struktúrájának változása között jön létre kölcsönhatás, amit a neutrínó közvetít. Mi teszi a neutrínót alkalmassá távolhatás közvetítésére? Ennek oka, hogy a neutrínó a foton fermion párjának tekinthető: ugyanúgy nincs töltése és tömege, és ugyanúgy fénysebességgel terjed a térben, és ugyanúgy rendelkezik impulzussal is. Az egyetlen különbség, hogy a foton egytengelyű forgás, míg a neutrínó két tengely körül forog. A neutrínó nulla tömegét és töltését a fénysebességű forgás elve a relativisztikus kovariancia elvére vezeti vissza, amely megengedi olyan kettős forgások kialakulását, melyben a töltés és tömeg operátorok nullatömegű és töltésű állapota jön létre.

Az elektron család három tagja

A mezőelméletekben a kölcsönhatást virtuális bozonok kibocsátása és elnyelése hozza létre. Gyenge kölcsönhatásban az elektron-müon-tau családban a bozon kibocsátás az eredeti részecske megszűnésével jár együtt, és keletkezik egy neutrínó is. Ez eltér az elektromágneses kölcsönhatás mechanizmusától, ahol fennmarad az eredeti töltött részecske, és az impulzusmegmaradás szabályából következőleg a foton kibocsátás-elnyelés folyamata fluktuációt idéz elő. Gyenge kölcsönhatásban viszont két új részecske képződik az eltűnő részecskéből, amiért a virtuális mechanizmusban a kibocsátás és visszanyelés helyett szétválás és visszaképződés valósul meg, Ennek folyamán az impulzus megmaradása nem idéz elő fluktuációt a részecske pozíciójában.

A fénysebességű forgás koncepciójának egyik kiemelkedő sikere, hogy értelmezni tudja az elektroncsalád tagjainak tömeg viszonyait, mindennek előtt a tau részecske tömegére ad pontos értéket, noha erre a részecskék Standard Modellje nem kínál magyarázatot. A modell szerint az impulzusnyomatékot a tömeg, a fénysebesség és a Compton sugár szorzata adja meg: az egyetlen tengely körül forgó W bozon esetén a momentum m_WR_Wc = ħ, míg a tau részecskénél a kettősforgás miatt m_τR_τc = ħ/2. Kapcsoljuk össze, a két összefüggést:

A fermiont alkotó kettősforgási frekvenciája a részecske határán kívül nullára csökken, ami sugárirányú Euler erőt hoz létre. Ennek hatására lép ki a W bozon egytengelyű forgása, melynek forgási sugara fénysebességgel növekszik. Ez a mozgás egy spirált hoz létre, amelynek frekvenciája annak mértékében csökken, ahogy a sugár növekszik. A frekvenciaváltozás integrálja azt adja ki, hogy φ szögelfordulás a sugarat e^φ faktorral növeli meg. A W bozon és a neutrínó, akkor tudja visszaalakítani a fermiont, ha a forgás fázisa visszatér az eredeti irányba, ami félfordulatonként történik meg. Az első félfordulatnál R_τ/R_W = e^π = 23,14. Mivel m_W = 80,395 GeV/c² a számított tömeg m_τ = 1,737 GeV/c² lesz, ami kevéssé tér el a mért 1,777 GeV/c² értéktől. A müont a W bozon második, az elektron a harmadik félfordulatával értelmezve 75 illetve 3,24 MeV/c² tömeget kapunk, ami eltér a kísérleti 105,7 és 0,511 MeV/c² értékektől, az eltérés különösen az elektronnál nagy, ott már csak nagyságrendi az egyezés. Ez arra utal, hogy a W bozon és a neutrínó újra összekapcsolódása nem pontosan az eredeti irányban történik, csak annak közelében, ahol az impulzus visszanyerés még bekövetkezhet. Mivel az elektron, müon és tau részecske tömege jelentősen különbözik, így a W bozon kilépésekor a szintén kibocsátott neutrínók impulzusa is nagyságrendileg fog eltérni. Ez avval jár együtt, hogy a visszaképződés csak az eredeti részecskét tudja regenerálni, és emiatt az elektron nem mehet át müonba, vagy tau részecskébe. Ez összhangban van az energiamegmaradás elvével is: a virtuális W kibocsátás csak átmenetileg töri meg az energiamegmaradás törvényét. A virtuális folyamatban ezt az teszi lehetővé, hogy a W bozon nagy tömegét a tér erős görbületéhez tartozó potenciális energia ellentételezi.  A tau és müon nem stabilisak, ez előbbi bomlási ideje 2,3·10^-13s, az utóbbié 2,2·10^-6s. Ezt úgy értelmezhetjük, hogy a virtuális szétválási és összekapcsolódási folyamatok során a tau és müon visszaképződése részleges, ilyenkor tovább fut a W bozon fázisa és a következő félfordulatnál hozza létre a kisebb tömegű elektron típusú részecskét a hozzá tartozó kisebb impulzusú neutrínóval együtt. A W bozon eltűnésének végállomása az elektron, ahol minden szétválást újra egyesülés követ, ennek oka egyelőre a téridő szerkezetének titka maradt.

Van-e kontakt kölcsönhatása a gravitációnak?

De mi a helyzet a gravitációval, milyen hatás tartja fogva a Holdat a Föld, a Földet a Nap körül? Van-e itt is egy kontakt kölcsönhatás, amely ezt megvalósítja? Ezt igyekszik értelmezni már száz éve a fizika valamilyen kvantumos mechanizmussal, mindmáig sikertelenül. A fénysebességű forgások részecske modellje ezt úgy értelmezi, hogy a kettős forgás nem marad teljesen a részecske határán belül, ennek parányi hányadát az Euler erő kiviszi. De ennek ára van: a külső tartományban a forgás frekvenciája lecsökken követve a Kepler törvényeket. Ez a forgás is c sebességgel terjed, amely tovább görgeti a tér görbületeit és a negatív előjelű, vonzó gravitációs potenciális energiát. Mivel a frekvencia lecsökken, így a kerületi sebesség nem éri el c-ét, amiért nem teljesül a tömeg létrehozásának feltétele, e nélkül pedig a kvantum sem jöhet létre, hiszen tömeg híján nem társul a gravitációs forgáshoz impulzusnyomaték. Kontakt kölcsönhatást közvetítő gravitációs mező tehát van, tehát létezik, de ez a mező nem kvantumos. Így teljesedik ki a koncepció, hogy minden távolhatás mögött van valamilyen kontakt kölcsönhatás is.

Vessük össze a bolygók keringését a Nap körül az elektronéval, amely az atom magja körül végzi végeláthatatlan pályamozgását. Mi tartja pályán az elektront? A kibocsátott és elnyelt virtuális foton felhők lökései. Ezek a lökések kvantumokban érkeznek. De mi tartja pályán a Földet a Nap körül? Ennek oka, hogy a tér a tömegek által megalkotott görbületi szerkezettel rendelkezik, melyben a mozgás a „terepviszonyokhoz” alkalmazkodik. Mivel a görbületek lerövidítik az utat, a testek úgy tudják megtalálni a legrövidebb mozgási pályát, ha a nagy görbületű tartományokba igyekszenek. Ebben hasonlítanak a fényre, amely a legrövidebb optikai úthosszat keresi.  A legrövidebb út keresése kényszeríti a Földet közelebb Naphoz, ahol nagyobb a görbület, azaz erősebb a gravitációs vonzás. A nagyobb vonzóerő gyorsuláshoz vezet, amellyel járó nagyobb impulzus eltéríti a mozgást a Nap felé haladástól, és az energiamegmaradás törvényének engedelmeskedve létrehozza a zárt elliptikus keringési pályákat. A tér görbületei folytonosan változnak, nincsenek szakadások, nincsenek kvantumok a részecskékből folytonosan kibocsátott gravitációs forgásokban. Mozgása során a tömeg magával hurcolja a térgörbületeket, amelynek kialakításához időre van szükség. Távoli kozmikus katasztrófák megkésett üzeneteiről tudósítanak a gravitációs hullámok a LIGO kísérletekben.

.