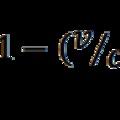Ha meg akarjuk ismerni a világot, kapcsolatba kell lépni vele: kölcsönhatásra van szükség. Ez a kölcsönhatás megváltoztatja a világot, miközben mi is megváltozunk. Ezek a változások vezetnek arra, hogy ismereteket szerezhetünk. Ez a kiindulópont. Ezután következik az absztrakció: eltekintünk a kölcsönhatástól és olyan törvényekbe, szabályokba foglaljuk az ismereteket, amelyek már függetlenek tőlünk, úgy mondjuk objektívek. De felmerül az örök kérdés: nem követünk-e el hibát, ha épp az információ forrását gondoljuk elhanyagolhatónak? De kérdezzünk tovább: van e határa ismereteink mélységének, pontosságának, van-e korlátja a megismerésnek? Ezeknek a kérdéseknek a megválaszolása választja szét a klasszikus és a modern fizika gondolkodásmódját!
Virtuális fogalmak megjelenése a modern fizikában
A modern fizika, mindenekelőtt a kvantummechanika szokatlan új fogalmakat használ. Nincs többé bizonyosság, csak valószínűségekről beszélhetünk a mikrorészecskék mozgásában és átalakulásában. Előjönnek olyan folyamatok, ahol virtuális fotonok fluktuációt hoznak létre a vákuumban, ahol virtuális részecske átalakulások valósulnak meg, ahol a foton létrehozhat nem megfigyelhető elektron-pozitron párokat, ahol valamilyen átalakulás előbb fejti ki hatását, mint amikor létrejött. Mit kezdjen a józan ész evvel az elrugaszkodott gondolkodással? Legyintsen rá mondva, ezek a fizikusok már maguk sem értik, hogy miről beszélnek? Vagy fogadja el, hogy vannak dolgok, melyek befogadása meghaladják saját képességeit, és csak a beavatottak tudják felfogni, hogy miről is van szó? Nehéz kérdés, de mégis vágjunk bele!
A folytonosság fogalma a klasszikus fizikában
Hogyan alakultak ki fogalmaink a klasszikus fizikában Galilei, Kepler és Newton korában? A távcsövekkel egyre pontosabban lehetett követni a csillagok és bolygók útját, de jól lehetett követni a leeső kő mozgását is, vagy mikroszkóppal a parányok világát. Az csak technikai részletkérdésnek tűnt, hogy milyen pontosan lehetett a mozgási pályákat leírni, és fel sem merült, hogy a megfigyelés bármit változtatna a mozgáson. Ez természetesnek tűnik, ha arra gondolunk, hogy egy parányi gyöngyszem is milyen óriási számú atomból áll. A mozgást azért tudjuk követni, mert a fény fotonjai a tárgy felületén bizonyos számú elektron pályáját megváltoztatják, ha ott elnyelődik, vagy visszaverődik. Az így átadott, vagy átvett impulzus hatása oly csekély, hogy ennek hatását legpontosabb műszereink sem tudják kimutatni. Emiatt alakult ki a meggyőződés, hogy a világról objektív törvényeket állíthatunk fel, és elvben ez a világ megismerhető és a megismerésnek csak technikai korlátai vannak. A mozgási pályát a tér és idő függvényében lehet megadni, amelyben mindegyik koordináta folytonosan változik. Ebben nyújtott a matematika is segítséget a folytonosság fogalmának megalkotásával, ami elvezetett a differenciálhányadoshoz is. Bár a gyakorlatban csak differencia hányadosokat határozhatunk meg, de ha elfogadjuk, hogy lehetséges a végtelenül kicsi változás is, akkor már differenciálhatunk is. A nagyobb változás leírása már nehezebb feladat, amikor a végtelenül sok apró változás hatását összesítjük az integráláskor. Bármely folytonos és differenciálható függvény, ha végtelenül kicsiny tartományt vizsgálunk, egyszerű lineáris változással írható le. Ebben az infinitezimális tartományban a fizika törvényei leegyszerűsödnek, ezen alapul Newton egyenlete is, amikor a pálya függvény második deriváltját, azaz a gyorsulást, arányosnak találta a testre ható erővel. Így jelent meg a mechanika differenciálegyenletek formájában. Ezt az utat követte később az elektrodinamika eljutva a Maxwell egyenletekig, és hasonló utat választott a termodinamika is. A klasszikus fizika a folytonosság és a teljes megismerhetőség feltevésén alapuló tudomány, melyben nemcsak a tér és idő folytonos, hanem folytonosak az energia és az impulzus is, a folytonosság uralkodik az elektrodinamikában és a termodinamikában is, ahol folytonos mennyiség az elektromos és mágneses mező, vagy a nyomás, hőmérséklet és entrópia.
A foton fogalma megteremti a kvantumot
A folytonosságra épülő klasszikus világkép a fény – azaz a fotonok – folytonos áradására épül, amelynek nincs hatása a megfigyelt tárgy, vagy égitest mozgására, a labda, ha elhajítjuk a sötétben, ugyanolyan pályán mozog mint világos nappal, legalábbis mi így gondoljuk, és erre építjük fel a mozgás folytonossági törvényeit. De van-e valamilyen határ, amelynél pontosabban nem mérhető a mozgás helye és sebessége? Technikai eszközökkel fokozhatjuk a pontosságot, de a gyakorlatban mindig marad egy korlát, amit nem léphetünk át. Ennek ellenére azt gondoljuk, hogy elvben a pontosság minden határon túl fokozható.
A modern fizika felismerte, hogy az anyag hullám természettel is rendelkezik. Ennek a hullámnak hossza és impulzusa összekapcsolódik, legyen szó akár fényről, vagy bármilyen részecskéről. De Broglie érdeme a végső felismerés: a két mennyiség szorzata – nem csak a foton esetén – a Planck állandóval egyenlő. Ezért ha a helymeghatározás nagyobb pontossága érdekében egyre rövidebb hullámokat választunk, ennek hatására a hullám impulzusa megnövekszik. A rövidebb hullám pontosabb pozíciómérést tesz lehetővé, ezért használunk Röntgen sugarakat a kristályok szerkezetének meghatározásakor, vagy ezért építünk elektronmikroszkópokat. Viszont minden ilyen mérés valamit megváltoztat a vizsgált anyagon azáltal, hogy meglöki és így megváltoztatja impulzusát. Ily módon a kölcsönhatás nagysága nem lehet bármilyen kicsi és ez a pozíciómérés pontosságától függ, azaz szembekerül egymással a két elv: a tetszőleges pontosság és a kölcsönhatás elhanyagolhatóságának kritériuma. Ezt fogalmazza meg a kvantummechanika a bizonytalansági relációban: a pozíciómérés és az impulzusmérés hibáinak szorzata nem lehet kisebb a Planck állandónál.
Milyen hipotéziseket alkalmaz a kvantummechanika?
Hogyan dolgozik a kvantummechanika, amikor az elektronok mozgását és elhelyezkedését vizsgálja egy molekulában? Először is feltételezéseket tesz! Feltételezi, hogy milyen atomok vannak a molekulában és feltételezi a benne lévő elektronok számát. Ekkor még nincs szó mérésről, mégis mondani akarunk valamit a szerkezetről és az elektronok eloszlásáról. Számba vehetjük a kölcsönhatásokat, mekkora a vonzóerő az atommagok és az elektronok között és hogyan taszítják egymást az azonos töltésű részecskék. Ez elég ahhoz, hogy az energia lehetséges értékeire és az atomok, illetve az elektronok eloszlására valószínűségi kijelentéseket tegyünk. Ezeket az információkat olvassa ki a kvantummechanika az állapotfüggvényből. Ahhoz már mérésre, például valamilyen fénnyel való besugárzásra, van szükség, hogy megállapítsuk a vizsgált molekula melyiket veszi fel a lehetséges energiaértékek közül. Az elektront szokás egyrészt hullámként, másrészt parányi gömbnek elképzelni, pedig ez a részecske se nem hullám, se nem „labda”. Amikor hullámra gondolunk a közeg apró elemeinek mozgását képzeljük el, de hát az elektron nem bontható tovább. Ha egy labda képe jelenik meg előttünk, azt annak köszönhetjük, hogy onnan folytonosan érkeznek a fotonok és így kirajzolódik szemünkben a gömbi forma és nyomon követhetjük a pályát is. Viszont az elektronok csak akkor adnak hírt magukról, amikor vagy elnyelnek, vagy kibocsátanak egy-egy fotont. Ennek hatására megváltozik állapotuk, amit már egy új állapotfüggvény, más eloszlás, más energia és impulzus jellemez. A görög filozófus szerint, nem lehet kétszer ugyanabba a folyóba belépni, az elektron is más lesz a megfigyelést követően. Ennek a változásnak mértéket adja meg az átvett, vagy leadott impulzus, és ha egy újabb mérést hajtunk végre (foton elnyelés, vagy kibocsátás), az ekkor nyert információ már az új állapotra vonatkozik, bizonytalanná téve, hogy mekkora lehetett az impulzus az első mérés során. Ezt fogalmazza meg a kvantummechanika, amikor kimondja, hogy egyidejűleg nem lehet teljes pontossággal meghatározni az elektron helyét és impulzusát.
Az állapotfüggvény redukciója
A méréskor, azaz a kibocsátott foton megfigyelésekor, már megmondhatjuk, hogy a vizsgált molekulának éppen mekkora az energiája, ez a lehetséges értékek egyike lesz. Ily módon megszűnik az eredeti állapotfüggvényből fakadó többértékűség, amikor csak az egyes mennyiségek valószínűségéről beszélhetünk. A koppenhágai iskola azonban más értelmezést ad, amikor az állapotfüggvény redukciójáról beszél, mintha a mikro rendszer „ugrana be” az egyik lehetséges állapotba a rendelkezésre álló választékból. Igazából csupán arról van szó, hogy a mérés nélkül nem tudhatjuk, hogy mekkora a molekula energiája, impulzusa és egyéb paramétere, csak ezek lehetséges értékeiről beszélhetünk. Méréskor viszont a nem-tudás, a feltételezés világából lépünk át a tudáséba!
Virtuális fotonok és átalakulások
Ugyanez a helyzet a modern fizikában, amikor virtuális fotonokról és átalakulásokról van szó. Amíg nem történik meg a tényleges mérés minden csak feltételezés, és itt a valószínűség matematikai szabályai érvényesülnek. Ebben a világban jogunk van a különböző feltételezésekhez, hiszen nem ténylegesen megvalósuló folyamatokról van szó, hanem interpretációról. Feltételezéseink kulcsot adnak, hogy sorra vegyük a lehetséges folyamatok sokaságát, de amíg nincs mérés, nincs információ: „szabad a gazda”. Ha viszont a virtuális világban jól építjük fel a lehetséges folyamatok sokaságát, akkor a tényleges méréseket, megfigyeléseket megfelelően tudjuk értelmezni, nem szabad azonban ezeket a feltételezett folyamatokat ugyanolyan követelményeknek alávetni, mint az olyanokat, amelyek ténylegesen végbemennek. Ezért jöhetnek szóba a kvantum-elektrodinamikában akár az oksági láncot is megszegő átalakulások, vagy lépnek fel fénysebességen túli virtuális mozgások. Elképzeléseink igazságát az mutatja meg, hogy a belőle levezetett összefüggéseket visszaigazolják-e méréseink, és képesek vagyunk-e általa olyan kísérleteket megtervezni, amelyek vagy igazolják, vagy cáfolják a feltételezett modellt. A modern fizika gondolkozási technika a mikrovilág értelmezésére: az elmélet akkor helyes, ha nincs benne ellentmondás és betartja a matematika szabályait.
Virtuális fogalmak a klasszikus fizikában
A virtuális fogalmak világa nem idegen a klasszikus fizikától sem, ahol virtualitáson azt értjük, hogy valamilyen fizikai entitás közvetlenül nem látható. Erről beszél a kvantum-elektrodinamika, amikor virtuális – azaz nem detektálható – fotonokkal írja le az elektromágneses kölcsönhatást. De honnan származik ez a fogalom? Ennek eredetét a klasszikus elektrodinamikára vezethetjük vissza. Mit is jelent például az elektromos mező? Evvel írjuk le az elektromos töltések közötti erőhatást, amit úgy definiálunk, mint az egységnyi töltésre ható erőt. De ez is feltételezés, mert oda képzelünk mindig egy egységnyi töltést, akkor is, ha a szóban forgó töltés körül nincs semmi, ha ott vákuum van. Más szóval az elektromos mező képzeletünk terméke, amely a kölcsönhatási képességet írja le, amiért ebben a tekintetben ez is virtuális fogalom. A fogalom bevezetésének előnye, hogy kitűnően képes leírni az elektromágneses jelenségek hosszú sorát. Az elektromos mező testvérfogalma a mágneses mező, amely a mozgó töltésektől származó járulékos erőhatást írja le. Ez a mező jól szemléltethető egy patkó mágnessel és vasreszelékkel: az egyes szemcsék kirajzolják, hogy merre haladnak a mágneses erővonalak. Ezáltal közvetett úton láthatóvá tettük a mágneses mezőt, de közvetlenül mégsem az erővonalakat látjuk, hanem a vasreszelék szemcséit, amelyek akkor is helyükön maradhatnak, ha közben a mágnest eltávolítjuk.
A kölcsönhatások leírása közvetlen kontaktussal
A klasszikus fizika úgy értelmezi az elektromágneses mezőt, mint a tér nem érintkező pontjai közötti erőhatást. A modern fizika azonban továbbmegy, amikor felteszi a kérdést: hogyan alakul ki az a mező, amely kapcsolatba hozza az elektromosan töltött részecskéket? Válasza az, hogy a tér egymástól távoli pontjai között úgy jöhet létre kölcsönhatás, ha van valamilyen közvetítő, amely közvetlen kontaktust hoz létre. Ezt a kontaktust a töltésből folytonosan kiáradó, és el is nyelődő fotonok teremtik meg. Ezek a közvetlenül nem látható virtuális fotonok is fénysebességgel haladnak, és ezért van, hogy a kölcsönhatási sebesség megegyezik a fénysebességgel. A fotonoknak két polaritása (spin állapota) van, amit a kibocsátó töltés előjele határoz meg. A fotonok „találkozáskor” szuperponálódnak: ha két azonos polaritású foton találkozik, akkor az amplitúdók összeadódnak, ellenkező esetben kioltják egymást. Ezáltal két azonos töltés kölcsönhatásakor a polaritás megegyezése a részecskék közötti tartományban „feldúsítja” a foton hullámokat. A fotonok impulzusuk által lökést gyakorolnak a töltött részecskékre, ami ebben az esetben taszításhoz vezet. Ha viszont ellenkező a töltések előjele, akkor a részecskék közötti tartományban kevesebb lesz a foton a kioltás miatt. A fotonok minden irányban egyforma valószínűséggel áramlanak ki és nyelődnek el, amiért a lökések hatása kiegyenlítődik és nincs mozdító erő, ha nincs valamilyen szuperpozíció.
Az állandóan kibocsátott és elnyelt fotonok folytonos lökéseket adnak a töltött részecskéknek, melyek pozíciója így fluktuálni fog, ezt hívja vákuumfluktuációnak a kvantum-elektrodinamika. Ez a fluktuáció avval jár, hogy a töltések által elfoglalt tartomány mérete kissé nagyobb lesz. A klasszikus elektrodinamika szerint a mágneses mező nagyságát a körbefutó töltések által leírt tartomány területe adja meg, ez a Maxwell-egyenletekből származtatható le. A fluktuáció a töltések által „bejárt” területet elektronok esetén 1,15%-kal megnöveli. Ez mutatkozik meg az elektron mágneses momentumának éppen ekkora megnövekedésében a Dirac egyenlethez képest (a relativisztikus kvantummechanika energiaegyenlete). A jelenséget leíró matematikának ez csak az első közelítése. A kvantum-elektrodinamika helyességének nagyszerű bizonyítéka, hogy a rendkívüli pontossággal (10 tizedes jegynyi!) meghatározott arányt az elmélet tökéletesen képes visszaigazolni.
A fizika mint gondolkodási mód
A fizika tudománya az objektív természet megismerése céljából kialakított gondolkozási mód. Ezen belül jelenik meg a modern fizikában a virtuális fogalmak rendszere. Valójában ez a megfigyelés közvetett voltát jellemzi: minél közvetettebb az információ, annál inkább játszanak fontos szerepet a virtuális folyamatok. Ezek megértése viszont nehéz, mert a közvetettség egyúttal távolodást is jelent megszokott fogalmainktól. Hajlamosak vagyunk rá, hogy ebben a világban is hasonló törvényeket várjunk el, mint ami megszokott mindennapjainkban. A megértésben segíthet, ha nem feledkezünk meg a közvetlenül látható, ha úgy teszik valóságos világ és az elképzelt világ eltérő arculatáról.
A blog további írásai elérhetők: Paradigmaváltása fizikában ...