Periodikus változások, mint a rezgések, vibrációk vagy hullámmozgások általános jelenségek mind a makro- mind a mikrovilágban. Megfigyelhetjük bármilyen fizikai közegben, legyen az szilárd, cseppfolyós vagy gáz, sőt még vákuumban is. Ennek sok formáját ismerjük a természetben, rezeghet egy húr, rezeghet a levegő is, ami a hang formájában érkezik fülünkbe, hullámzik a víz, de rezeg az elektromágnesesség is a rádióhullámoktól kezdve a látható fényen át a gammasugarakig. Bizonyos objektumok egyes részei külön-külön is rezeghetnek, erre példa a molekulák kötéshosszának rezgése, a vibráció. De gyakran általánosítjuk a hullám fogalmat az élet, a társadalom és a gazdaság jelenségeire is. Mi a közös és mi az eltérő ezekben a periodikus jelenségekben? Ezt a kérdést taglalja a következő írás.
A periodikus változás jellemzői
Az első kérdés, amit fel kell tenni, hogyan jellemezzük a periodikus változásokat. Ennek egyik típusa a rezgés, amikor a periodikus mozgás helyhez kötött, a másik a hullám, amikor valamilyen közegben tovább terjed az időben ismétlődő változás. A hullámnak három fő jellemzőjét emelhetünk ki: a periodikusság térbeli és időbeli hosszát és a haladás sebességét. A térbeli ismétlődés egysége a hullámhossz, amit λ-val jelölünk, az időbeli hossz a „T” periódus idő, amelynek reciproka az „f” frekvencia, végül a sebesség, aminek szokásos jelölése „c” a latin celeritas után. A három mennyiség azonban nem független egymástól, mert a hullámhossz és a frekvencia szorzata a sebesség:λ·f = c. A hullámzás mértékének további jellemzője az „A” amplitúdó és a φ fázis, ami megjelenik a hullám matematikai leírásában. Ha az idő függvényében írjuk le a hullámot, akkor az A·cos(2πf·t+φ), ha az „x” térkoordináta mentén, akkor az A·cos(2πc·x/λ+φ) függvényeket használjuk. Gázokban és folyadékokban a rezgési amplitúdó a haladási irányba mutat, ezt nevezik longitudinális hullámoknak, míg szilárd közegben a kitérés iránya lehet a haladási irányra merőleges is, ez a tranzverzális hullám. A tranzverzális hullám sebessége eltér és általában lassabb, mint a longitudinális. Erre ismert példa, ahogy földrengés esetén a longitudinális hullámok hamarabb érkeznek meg, mint a tranzverzális rezgések, az előbbiek emellett rövidebb utat járnak be, mert a Föld elasztikus magján is áthaladhatnak.
Rezgések szilárd közegben
Hogyan hozhatunk rezgésbe egy testet és mi határozza meg a rezgés frekvenciáját? Szilárd testeknél az alaktartósság a kiindulópont, ebben különbözik a folyadékokban és gázokban létrejövő hullámoktól. Az alaktartás egy erőt jelent, amely a testet eredeti alakjába hozza vissza és ez az erő határozza meg, hogy mekkora lehet a rezgés frekvenciája. Az erő jellemzője a rugalmassági modulus, amely kapcsolatot teremt a test méretváltozása, például a Δl megnyúlás és az ahhoz szükséges erő között, ami egy határon belül arányos egymással a Hook-szabály szerint: F = k· Δl. A molekulák szintén alaktartó fizikai objektumok, melyeket az atomok közötti kötéstávolság és kötésszög jellemez. Itt az alaktartáshoz tartozó erőt a kémiai kötés erőssége határozza meg.
A rezgések és hullámok csillapodása
Van azonban egy döntő különbség a makro- és a mikrovilág objektumai között: az előbbiben a hullám, vagy rezgés előbb utóbb elhal, csillapodik, ha nem érkezik újabb lökés, míg az utóbbi „örök” rezgésre van ítélve, amit a kvantummechanika zérusponti rezgésnek nevez. Ennek oka, hogy a makroszkopikus objektumokban a periodikus mozgás rendezettsége előbb-utóbb az egyes molekulák rendezetlen mozgásába megy át különböző véletlenszerű kölcsönhatások eredményeként. Ez a termodinamika entrópia növekedési törvénye, amely előírja, hogy a testekben a molekulák „kollektív” mozgásához tartozó mechanikai energiája átalakul rendezetlen mozgások hőenergiájává. Az entrópia fogalma a nagyszámok törvényéhez kapcsolódik (lásd: „Szimmetria jelenségek a mindennapokban és a modern fizikában”), és ez meghatározza, hogy az egyes vibrációk hányad része lehet „gerjesztett” illetve alapállapotban. Az egyedileg kiszemelt vibrációra azonban nem alkalmazható az entrópia elv, hiszen az mindig nagyszámú részecske eloszlását írja le. Ha a vibrációs állapotok száma eltér az egyensúlyi értéktől, akkor az átmenetek száma úgy alakul, hogy a mikroállapotok által képzett makroszkopikus fizikai mennyiség (például paramágneses rendszerben a mágnesezettség) közeledni fog az egyensúlyi értékhez. Bár minden egyes átmenet kvantált, a makroszkopikus paraméter mégis folytonosan változik, mert a molekulák óriási száma miatt az egyes ugrási lépcsőfokok a kis értékük miatt nem detektálhatók.
Kvantummechanikai mozgások a valószínűségi mezőben
A kvantummechanika minden egyes vibrációs állapotot – az alapállapotot is beleértve – hullámfüggvény periodikus változásával írja le, de ez a mozgás nem „látható”, mert a stacionárius (időben nem változó energiájú) állapotok nem bocsátanak, illetve nem nyelnek el fotonokat. A vibrációról mégis nyerhetünk információt, ha Röntgensugarakkal bombázzunk kristályokat. Ilyenkor az atomok térbeli elrendezését határozhatjuk meg, ahol az egyes atomok helyét meghatározó „foltok” nagysága tükrözi a vibrációs amplitúdót. Ez azonban nem időben jellemzi a vibrációt, hanem térbeli eloszlásán keresztül, megmutatva, hogy az egyes pozíciókat az atom mekkora valószínűséggel foglalja el. Úgy is fogalmazhatunk, hogy amíg a klasszikus mechanika időben ábrázolja a vibrációt, addig a kvantummechanika valószínűségi mezőben írja le a mozgást (lásd: Miért diszkrétek az energianívók kötött állapotban). Mivel a valószínűségi mezőben végbemenő mozgás nem jár detektálható fotonok kibocsátásával, vagy elnyelésével, a periodikus mozgás nem fog csillapodni.
A rugó rezgései
Rezgést egy szilárd testben úgy hozhatunk létre, ha energiát közlünk vele, ez lehet egyszeri, amikor egy kalapáccsal egy fémtárgyra ütünk, vagy meghúzunk egy rugót, de lehet periodikusan ismétlődő hatás is, például a hinta mozgásánál, amit megfelelő ütemben hajtunk meg, vagy centrifugáláskor, amikor a mosógépünk rázkódni kezd.
Nézzük meg a rugó példáját. Tegyünk rá egy súlyt, amitől megnyúlik. A ráható erő nagyságával lesz arányos a megnyúlás, legalább is egy határig. Ekkor a Δl megnyúlás kifejezhető Δl = k·m·g összefüggéssel („m” a tömeg, „g” a nehézségi gyorsulás). Ezen alapul a rugós mérleg is, amikor ismert súlyokkal kalibráljuk a mérleget és az így meghatározott skálát használhatjuk a súly, azaz a tömeg mérésére. De mérhetünk-e tömeget az űrhajóban, ha az a súlytalanság állapotában van? Ott hiába akasztunk egy tárgyat a rugóra az nem fog megnyúlni a gravitációs erő hiányában, de meghúzhatjuk a rugót a tárggyal együtt, majd engedjük el a tárgyat, ekkor a rugó rezgésbe jön, majd néhány rezgés után a mozgás megszűnik. Ez lehetőséget ad számunkra, hogy mérjük az időegység alatti rezgések számát, azaz a frekvenciát. A frekvencia a „k” erőállandó és a tömeg arányától függ. Ezt az összefüggést a Newton féle mozgástörvényből származtathatjuk, mely szerint a gyorsulás a testre ható „F” erővel arányos. Ennek differenciálegyenlete:
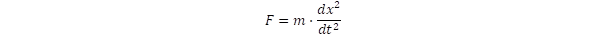
ahol „x” jelöli az egyensúlyi helyzettől való kitérést. Az egyensúlyi helyzetéből kimozdított rugót a rugalmas erő visszahúzza eredeti pozíciója felé, amit negatív előjellel vehetünk figyelembe, azaz F = -k·x. A differenciálegyenletnek eleget tevő periodikus függvény:
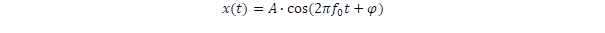
ahol f0 a saját-, vagy rezonanciafrekvencia és φ a fázis:
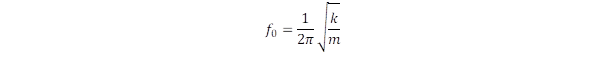
A frekvencia tehát nem függ a kitérés „A” amplitúdójától, csak a „k” erőállandó és az „m” tömeg arányától. Ha a rugó saját tömege elhanyagolható a mérendő test tömegéhez képest, akkor ez az összefüggés módot ad rá, hogy a súlytalanság körülményei között is meghatározzuk a tárgy tömegét.
Az ingamozgás
A sajátfrekvencia más példája az inga, vagy a hinta esete, mert ekkor nem az anyag rugalmas ereje hozza létre a lengést, hanem a gravitációs erő. Ha az „l” hosszúságú matematikai inga alfa szöggel kitér a függőleges iránytól, akkor a nehézségi erő érintő irányú komponense, azaz m·g·sinα erő fogja visszahúzni az ingát az egyensúlyi helyzet felé. A kilengés amplitúdóját az x = l.α ívhosszal jellemezhetjük és írjuk fel a mozgásegyenletet az alfa szöggel: α = x/l . Ha nem túl nagy a kitérés szöge, akkor sinα megegyezik a radiánban mért alfa kitérési szöggel, ebben a közelítésben a Hook-szabálynak megfelelő arányosságot kapunk, melyben k = m·g/l lesz. Ezt beírva a frekvencia kifejezésébe a k/m = g/l egyenlőséghez jutunk, azaz az inga segítségével a Föld különböző pontjain mérhetjük a helyi nehézségi gyorsulás nagyságát.
A hullámok terjedési sebessége
Mechanikai hatásokkal bármely szilárdtest rezgésbe hozható, csak az a kérdés, hogy a rezgés meddig marad fent. Ennek a rezgésnek nem a frekvenciája jellemző a közegre, hanem a hullámok terjedési sebessége, amely a közeg rugalmasságától és sűrűségétől függ. Itt azért a sűrűség játszik szerepet, mert a külső deformáló erő miatt fellépő belső nyomás egyenletesen oszlik el a közegben és ez hozza mozgásba a homogén eloszlású tömeget. Az összefüggést leíró Newton-Laplace formulában szerepel a nyomás dimenziójú k’ rugalmassági modulus és a ρ tömegsűrűség:

A sebességnek eltérő értéke van longitudinális és tranzverzális rezgésnél, mert a hullám haladására merőleges rugalmassági modulus (nyírás irányú) gyengébb, mint a haladási irányú. A longitudinális sebesség vasban 5120 m/s, ami tetemesen meghaladja a hangterjedés sebességét vízben (1484 m/s), vagy levegőben (343,2 m/s), annak ellenére, hogy a vas sűrűsége a három közeg közül a legnagyobb. Ennek oka a nagy rugalmassági modulus, ami jóval meghaladja a víz, illetve a levegő nyomással szembeni kompressziós modulusát.
A zenei „a” hang
Folyadékokban és gázokban is érvényes a Newton-Laplace formula, ahol csak longitudinális hullámok jöhetnek létre, ha eltekintünk a víz felszínén kialakuló hullámoktól. A levegőben tovaterjedő sűrűsödések és ritkulásokat érzékeljük fülünkkel, ahol a periodikus változás frekvenciája határozza meg a hangmagasságot. Vegyünk egy 39 cm hosszú húrt és pengessük meg. Mit fogunk hallani? Ekkor is rezgések jönnek létre, amelynek hullámhossza a húr hosszúságához igazodik. Ha a húr két végét rögzítjük, akkor csak a húr közepe fog kitérni, amiért az alaphang hullámhossza a húr hosszának kétszerese lesz. A hullám terjedési sebességét figyelembe véve ez 6564 Hz-nek felel meg, ami rendkívül magas hang. Mi azonban csak a levegő rezgéseit hallhatjuk, mert a húron végigfutó longitudinális rezgések nem lökik meg a levegő molekulákat, erre csak a húr irányára merőleges kitérés képes. Ez viszont a levegőben 343,2/0,78= 440 Hz frekvenciájú rezgést produkál, ami megfelel a normál „a” zenei hangnak. Azonban a zenészek nem valamilyen húrt használnak a hangoláshoz, hanem a hangvillát, mert a húroknál kritikus a hőmérséklet és a rögzítés állandósága, emellett még zavarnak az intenzív felharmonikusok is. A hangvilla két ágának rezgési frekvenciája viszont kevéssé függ a körülményektől és értékét a villa szárainak hosszúságán kívül annak anyaga (sűrűség és rugalmassági modulus) és keresztmetszete határozza meg.
Molekuláris mozgások és rezgések
Az anyagok makroszkopikus tulajdonságai visszavezethetők a molekulák energia eloszlására. Jelöljük Ei-vel az egyedi molekulák energiaszintjeit. Szilárd testekben ezt a helyhez kötött mozgások, azaz a vibrációk határozzák meg, gázokban ehhez még hozzájárul a helyváltoztató mozgások energiája is, míg folyadékban a helyváltoztató mozgásoknak bizonyos fajtái jöhetnek létre. A lehetséges mozgástípusokat nevezzük a molekulamozgás szabadsági fokának. Egyensúlyi állapotban az Ei energiájú molekulák számát a hőmérséklet határozza meg, jelöljük ezt Ni,e-vel. Közöljünk energiát a rendszerrel, például úgy, hogy egy tárgyra kalapáccsal ráütünk, ha az szilárd, vagy egy dobra ütve hozzuk rezgésbe a levegőt. Molekuláris szinten ez azt jelenti, hogy megváltozik az Ei energiájú molekulák száma valamilyen Ni(0) értékre. A véletlenszerű mozgások kölcsönhatásba lépnek egymással (például gázokban ütköznek a molekulák), amely fokozatosan úgy változtatja meg az eloszlást, hogy az közeledni fog az egyensúly felé. Homogén anyagszerkezet esetén egyetlen T időállandóval jellemezhetjük ezt a változást, amely kimondja, hogy a változás sebessége arányos az egyensúlyi eloszlástól való eltéréssel:

Ez a differenciálegyenlet exponenciális közeledést ír le az egyensúly irányában:
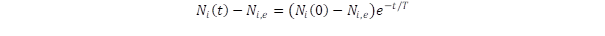
Az egyes molekulák energiáját összegezve kapjuk a teljes energiát, ami ugyanevvel a „T” időállandóval közeledik az egyensúly felé. Ha a vizsgált tárgy rezgéseket végez, vagy egy gázban, illetve folyadékban követjük a hullámok terjedését, akkor az amplitúdó időbeli csökkenését a „T” időállandó határozza meg. Hasonló jellegű a csökkenés, amikor mágnesezettséget gerjesztünk periodikusan változó mágneses mező segítségével. (A molekulák vagy atomok mágneses dipólus momentumai hozzák létre a mágnesezettséget a mágneses mező hatására, ezt hívjuk paramágnesességnek) Valamennyi felsorolt esetben, ha kilökjük a rendszert az egyensúlyi állapotból, akkor ezt követően exponenciálisan fog a rendszer közeledni az egyensúlyhoz. Matematikailag ez azt jelenti, hogy a mozgás differenciálegyenletében fellép egy az idő szerint képzett első differenciálhányadosával arányos tag:
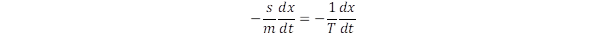
Ha az „x” változó valamilyen irányban való elmozdulást jelöl, akkor a fenti kifejezés sebességgel arányos fékező hatást ír le. Mozgó járműveknél „s” a sebesség szorzója, amely kifejezi a súrlódás, vagy közegellenállás által okozott fékezési erőt, amelynek hatására, ha kikapcsoljuk a járművet meghajtó motort, akkor a jármű exponenciálisan lassul T = m/s időállandóval. Ha viszont mágneses jelenségeket vizsgálunk, akkor az „x” változó mágnesezettségnek felel meg és a csillapítási mechanizmus a relaxáció jelensége. A fenti energiaveszteségi tag okozza a rezgések és hullámok exponenciális amplitúdó csökkenését:

Ezt hívjuk csillapított rezgésnek, amely során a mozgási energia hőenergiává alakul át. Az f’ frekvencia eltér az f0 sajátfrekvenciától a csillapítás hatására: f’2 = f02 – 1/4T2. Az ábra mutatja a 10 Hz rezgés lefutását, ha a T csillapítási idő 0,5 s.
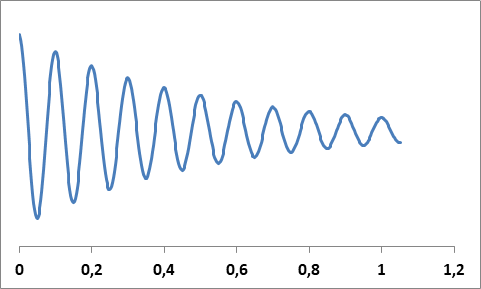
Itt a vízszintes skála az idő másodpercben megadva.
Kényszerrezgések
Amikor periodikus erőhatást gyakorolunk egy testre, akkor rákényszeríthetjük az alkalmazott frekvenciát, ez a kényszerrezgés. Ennek is van egy átmeneti szakasza, amit a „T” csillapítási idő határoz meg, de most foglalkozzunk az egyensúlyi válasszal. Ennek mértéke attól függ, hogy mennyire vagyunk közel a rendszer sajátfrekvenciájához. Ha épp egyezik evvel az alkalmazott frekvencia, akkor rezonanciáról beszélünk. A periodikus erő kifejezését a következő alakban adhatjuk meg:
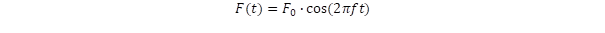
Az egyensúly beálltakor az „f” frekvenciával gerjesztett rezgés amplitúdója fejezi ki a rezonanciát:

A második, egyszerűsített függvény a Lorentz görbe, illetve a Cauchy eloszlás. Példaként nézzük meg a rezonanciagörbét a korábbi lecsengést bemutató esettel, amikor is a sajátfrekvencia 10 Hz és a csillapítási idő 0,5 s:
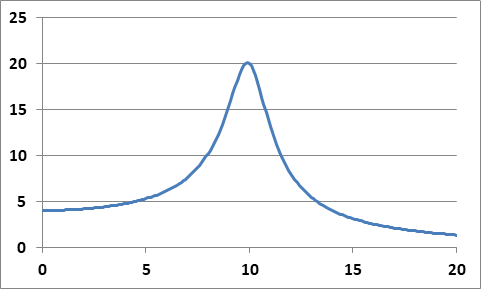
Itt a vízszintes skála a frekvencia Hz egységben. A rezonanciagörbe élességét és az erősítés hatásfokát az f0/T arány határozza meg, ami a fenti példában 20.
Mérések egyszeri és periodikus gerjesztéssel
A fizikai méréstechnikának két alaptípusa van, az egyikben meglökjük a rendszert és követjük az egyensúly időbeni visszaállását, a másikban valamilyen új egyensúlyi helyzetet hozunk létre. Legegyszerűbb példa erre a már említett súlymérés, ahol vagy a lengési frekvencia, vagy a megnyúlás mértéke ad felvilágosítást a súly nagyságára. A mérési pontosság szempontjából alapvető a „fékezés” hatása. Ha túl gyors a csillapodás, akkor kevesebb lengés alapján kevésbé pontos értéket kapunk a frekvenciára. Ha pedig a megnyúlást vizsgáljuk, akkor az erős csillapítás miatt a rugó nem éri el a teljes megnyúlást, mert már előbb lefékeződik. Pontos mérés tehát gyengébb csillapítást igényel, de ekkor a hosszabb mérési idővel fizetünk a nagyobb pontosságért.
Példák a mechanikai rezonanciára
Mechanikai rezonancia okozta Broughton híd leszakadását, amikor a katonák lépéstartással meneteltek át rajta 1831 április 12-én. A függő híd 44 méter távolságú felfüggesztéséhez 88 m hullámhossz tartozik. A tranzverzális rezgés saját frekvenciája 2 Hz körül lehetett megegyezve a menetelés ütemével.
Másik sokat emlegetett hídkatasztrófa a Tacoma Narrow Bridge esete, amelyik a szél hatására jött rezonanciába 1940 november 7-én, itt a felfüggesztési távolság 853 méter és a torziós rezgés saját frekvenciája 0,2 Hz volt. A katasztrófa eredeti magyarázatát von Kármán Tódornak köszönhetjük, akinek a vortex elméletét vették alapul annak magyarázatához, hogyan alakult ki a hídon torziós oszcilláció. Később a magyarázatot pontosították nem-lineáris hatások figyelembe vételével.
Mágneses rezonancia
Mágneses rezonanciát hozhatunk létre ha az anyagokat mágneses mezőbe helyezzük és egyúttal mikrohullámmal (ESR = Electron Spin Resonance vagy EPR = Electron Paramagnetic Resonance), vagy rádiófrekvenciával (NMR = Nuclear Magnetic Resonance) sugározzuk be. A kölcsönhatás alapja, hogy az elektronok, illetve bizonyos atommagok (például a proton) saját mágneses momentummal rendelkeznek. Mágneses mezőben a mágneses dipólus momentumok diszkrét energia értékeket vesznek fel és ezek különbségét osztva a „h” Planck állandóval kapjuk meg a rezonancia frekvenciát: f0 = ΔE/h. A rezonancia akkor lép fel, amikor a sugárzási frekvencia egyezik az f0 értékkel. A hagyományos spektroszkópiában a mágneses mező folytonos változtatásával veszik fel a rezonancia jelet, de elsősorban az NMR-ben már rádiófrekvenciás impulzusokkal „lökik” meg a mágnesezettséget és a lecsengő mágnesezettség jeléből egy matematikai művelettel (Fourier transzformáció) állítják elő a jelalakot. Az elektron mágneses tulajdonságát elveszíti, ha a kémiai kötésben elektronpárok alakulnak ki, de előfordul bizonyos anyagokban (szabad gyökökben és egyes átmenetifém vegyületekben), amikor egyes elektronok „pár nélkül” maradnak, ekkor alkalmazható az ESR spektroszkópia. Az atommagok jelentős része rendelkezik mágneses momentummal, így a proton és a 13C izotóp is, ami alkalmassá teszi az NMR spektroszkópiát szerves molekulák szerkezetének felderítésére. Az orvosi diagnosztika egyik fontos vizsgálati eszköze – az MRI képalkotás (Magnetic Resonance Imaging) – az NMR rezonancián alapul. Hidrogén atommagok rezonanciája révén rajzolódnak ki az anatómiai részletek azokban a szervekben, melyekben magas a víz, vagy zsírtartalom.
Elektromágneses hullámok és rezonanciák
Mechanikai rezgések, hanghullámok és molekulavibrációk esetén a hullámok létrejötte a molekulák, vagy atomok mozgásához van kötve. Más a helyzet az elektromágneses hullámokkal, illetve a fénnyel, amely vákuumban is terjed. Ennek példája, ahogy rádiónkkal, vagy a TV-vel a távoli adó által kibocsátott sugárzást vesszük. Ez is rezonancia jelenségen alapul, amikor a vevő rezgőkörének frekvenciája egy adó frekvenciájára van hangolva. De mi az a „közeg” ami hordozza a rezgést, mi az ami mozog az üres térben, a vákuumban?
A klasszikus elektrodinamika válasza, hogy az elektromos és a mágneses mező rezgéseit látjuk, amely „c” fénysebességgel terjed. Ezt avval egészíti ki a kvantummechanika, hogy bevezeti a foton fogalmát, mint az elektromágneses hullám legkisebb egységét. Tekinthetjük-e az elektromos és a mágneses mezőt, vagy a fotonokat ugyanolyan anyagnak, mint az elektront, a protont és a többi részecskét? Ha az anyag fogalmát a tömeggel azonosítjuk, akkor mondhatnánk, hogy ezek a mezők nem anyagiak, csupán matematikai leírásunk termékei, hivatkozva arra, hogy a fotonnak nincs nyugalmi tömege. De erre válaszul ott van a relativitáselmélet legfontosabb képlete, a nevezetes E = m·c2 összefüggés. Ebből az következik, hogy mivel a foton rendelkezik energiával, így van tömege is, csak ez a tömeg nem nyugalmi, hanem épp a fénysebességű mozgás eredménye.
Lehet-e a tér az elektromágneses sugárzás fizikai közege?
További kérdés, hogy miért állandó a fénysebesség, miért nem mozoghat semmilyen fizikai objektum ennél nagyobb sebességgel? Keressünk ehhez párhuzamot a levegőben, vagy más közegben terjedő hanghullámok esetével! A Newton-Laplace egyenlet szerint bármely homogén közegben a hullám terjedési sebessége 4π2c2 = k’/ρ, ahol k’ a közeg rugalmasságát jellemző nyomás dimenziójú mennyiség és ρ a sűrűség. Állítsuk ezt párhuzamba a fénysebességgel, amely megadható c2 = E/m formulával a relativitáselmélet szerint. Ha egy pontból fényt bocsátunk ki, akkor az c·t sugarú gömböt tölt meg a Huygens által megfogalmazott fényterjedési elmélet szerint. Osszuk el evvel a térfogattal az energiát és tömeget, ekkor kapjuk az ε energia és a ρ tömegsűrűséget, evvel átírva a tömeg és energia kapcsolatát írhatjuk, hogy c2 = ε/ρ . Ez már közelebb van a hanghullámok sebességképletéhez. Vegyük még figyelembe, hogy az ε energiasűrűség nyomás dimenziójú mennyiség, valamint, hogy a fénynek is van nyomása a kísérleti tapasztalatok szerint, akkor már nem tűnik indokolatlannak, ha az ε energiasűrűséget párhuzamba hozzuk a közegek rugalmasságát jellemző k’ állandóval. Az analógiából tehát az következik, hogy a tér egy fotonokkal feltöltött közeg, amely a fénynyomáson keresztül rugalmassági állandóval rendelkezik, míg a fotonok mozgási tömege képezi a közegnek tekintett tér sűrűségét.
Lehet-e dobozba zárni a fényt?
De fel lehet-e tölteni tényleg a teret fotonokkal? A válasz igen, aminek a technikai megvalósítása a mikrohullámú üreg. Képzeljünk el egy jól vezető fémekből álló üreget, például egy kockát, amelybe elektromágneses hullámokat bejuttatva a hullám az üreg falán visszaverődik. Ilyenkor állóhullámok alakulnak ki. Úgy viselkedik az üreg, mint a trombita, vagy a hegedű hangdobozának belső tere, amelyben a hanghullámok ide-oda verődése hoz létre állóhullámokat. Ha az üreg mérete 3 cm, akkor ennek rezonancia frekvenciája 1010 Hz lesz. Ezt nevezik X-sávú mikrohullámú rezonátornak. Az üreg anyagától függ a jósági tényező, ami azt jellemzi, hogy hányszor verődhet egy foton a falhoz, mire elnyeli a fém. Már sikerült 106 értékű jósági tényezőt is elérni, ami azt jelenti, hogy a betáplált energia 0,1 milliszekundum alatt csökken a felére. Az elektromágneses hullámokkal feltöltött tér, tehát olyan realitás, amely alátámasztja az elképzelést, amely magát a teret tekinti az elektromágneses sugárzás fizikai közegének, és nincs szükség arra, hogy feltételezzünk bármiféle „étert”.
A blog egyéb írásainak összefoglalása a megfelelő linkekkel együtt megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben.


