Ha elutazunk valahova és ha repülünk, akkor súlyunk eltér a megszokottól a fizika törvényei miatt még akkor is ha eltekintünk az élet szokásos jelenségeitől (anyagcsere, párolgás). A súly ugyanis a tömegre ható erő, amelyik más és más a Föld különböző pontjain és különböző magasságban. Ennek okait érdemes végiggondolni.

Mi a különbség a súly és a tömeg között?

Mindenekelőtt a tömeget és a súlyt kell megkülönböztetni, súlyról akkor van szó, amikor arról az erőről beszélünk, amely a tömegre hat itt a földön. Ez alapvetően a Föld gravitációs vonzásától származik, de ezen kívül figyelembe kell venni a Nap és a Hold hatását, valamint a Föld keringése és forgása miatt kialakuló erőhatásokat is. Amikor súlyról beszélünk, ne kétkarú mérlegre gondoljunk, hiszen ekkor a méréshez használt súlykészlet elemei azonosan változnak a mérendő súllyal, hanem rugós mérlegre. Ha ennek pontossága elég jó, akkor magunk is láthatjuk súlyunk változását, amikor utazunk, vagy a Föld különböző pontjain vagyunk.

A Newton-féle gravitációs törvény

A gravitációs törvény szerint az „R” távolságban lévő „m” és „M” tömegek között ható vonzóerő:

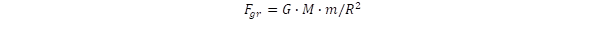
 ahol G = 6,674.10^-11m³kg^-1s^-2 az általános gravitációs állandó.

A Nap, Hold és a Föld gravitációs viszonya

Vizsgáljuk meg a különböző erők nagyságrendjét a Föld, a Nap és a Hold tömege és az átlagos keringési sugarak alapján, a Föld esetén a bolygó sugarát vegyük alapul.

A Föld felszínén a súlyt a „g” nehézségi gyorsulással jellemezhetjük:

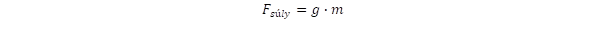
Ezt visszavezethetjük a gravitációs törvényre, ha gondolatban a Föld egész tömegét a középpontba helyezzük és a Föld sugarát helyettesítjük az összefüggésbe:

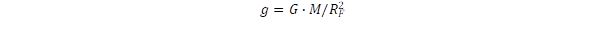
Az innen számolt nehézségi gyorsulás g = 9,844 m/s², jó közelítésben egyezik a földön mérhető középértékkel. A g nehézségi gyorsulás ugyanis a földrajzi helyzettől és a felszíni magasságtól is függ. Az előbbi oka, hogy a Föld forgásának kerületi sebessége a délkörök mentén más és más.

Az árapály jelensége

Jól ismert az árapály jelensége a tengerek és óceánok partvidékén, amit a Nap és a Hold helyzetének változása hoz létre a Föld forgása miatt. Vizsgáljuk meg, hogy a Nap és a Hold mekkora erővel hat a földi testekre. Ennek összehasonlítására szolgál a táblázat utolsó oszlopa, amelyben a Földhöz viszonyítjuk az adatokat. Látható, hogy a Nap vonzóereje jóval nagyobb, még pedig 178-szorosa a Holdénak, de még ez is jóval gyengébb, mint a Föld gravitációs ereje. Egy 100 kilogrammos ember esetén ez 60 gramm súllyal egyenértékű. Vajon ez azt jelentené, hogy délben, amikor ez a vonzás levonódik a földi gravitációból, (ekkor a Nap vonzása fölfelé mutat), ennyivel könnyebbek lennénk, míg éjfélkor (ekkor a Nap vonzása lefelé mutat) ennyivel nehezebbek? Erről azonban nincsen szó, mert körforgásnál a centrifugális erő:

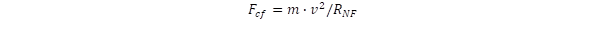
éppen kiegyenlíti a Nap gravitációs erejét. Itt a Föld átlagos keringési sebességét (30 km/s) és átlagos távolságát a Naptól kell figyelembe venni az erő számításánál. (A sebességet m/s, a távolságot méterbe átszámítva az erőt Newton egységben kapjuk, és 9,844 Newton felel meg 1 kilogramm tömeg súlyának.)

Ha ennyiszer nagyobb a Nap vonzóereje, akkor miért a Hold árapály hatása lesz 2-3-szor nagyobb a Naphoz képest, tehetjük fel a kérdést. Az árapályról szóló szócikkekben (például a Wikipediaban) erre nem kapunk pontos magyarázatot, csak annyit említenek meg, hogy a Hold kisebb távolsága az ok.

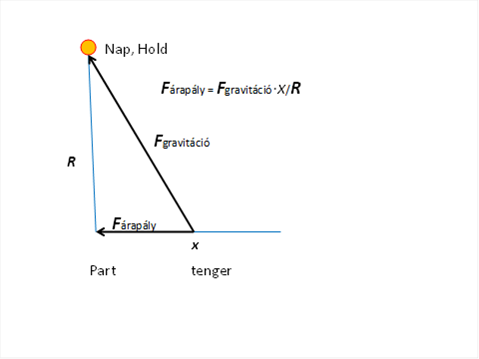
Képzeljük most magunkat a tenger partjára, amikor vagy a Hold, vagy a Nap épp a fejünk felett van. Milyen erőhatást gyakorol az égitest arra a víztömegre, amelyik tőlünk „x” távolságra van? Az ott ható erő nem lesz függőleges, hanem lesz egy a part felé mutató komponens is. A függőleges komponenst a centrifugális erő kiegyenlíti, de ez nem történik meg a vízszintes komponenssel, amely ezért a tenger vizét a part felé húzza. Apály esetén megfordul a helyzet, ekkor a part közeléből fogja a Nap vagy Hold vonzóerejének vízszintes komponense a vizet a mélytenger irányába húzni. Ez a vízszintes komponens a parttól való „x” távolság és az égitest „R” távolságának hányadosával lesz arányos és evvel a hányadossal kell szorozni az égitest gravitációs vonzóerejét. Mivel a Hold 390-szer közelebb van hozzánk, mint a Nap, így a part felé húzó erő számításánál ezt is figyelembe kell venni, ami így a Hold esetén 2,2-szer nagyobb lesz, mint amit a Nap hoz létre.

Súlyveszteség a repülőgépen

Szálljunk most fel egy repülőre és utazzunk el valahová. A fel és leszálláskori gyorsulást és lassulást ne vegyük figyelembe csak a magasságot és az útirányt. Ha 10 km magasan repülünk, akkor a Föld középpontjától mért távolságunk 6381 kilométer lesz, a négyzetes szabályt alkalmazva ez 100 kilós embernél 314 gramm súlycsökkenést fog okozni. Megérkezéskor is más lesz a súlyunk, attól függően, hogy északra vagy délre utaztunk. A tengerszint feletti magasságtól is függ súlyunk, így La Pazban 4000 méter magasan már számottevő a csökkenés, de most számoljunk tengerszinti magassággal és vizsgáljuk meg a délkörtől való függést. Ennek oka a Föld forgása miatt fellépő centrifugális erő, amelynek értéke függ a délkör szögétől a földfelszín kerületi sebességének változása miatt.

Súlyveszteség az egyenlítőnél

Az egyenlítőnél a legnagyobb a centrifugális erő, ahol a Föld 40 000 km kerülete 24 óra alatt fut körbe, ezért ott a kerületi sebesség v = 1667 km/h = 463 m/s. Evvel számolva a 100 kg súlyú ember súlya 337 grammal lesz kevesebb. Szálljunk fel ott egy repülőre és haladjunk kelet felé. Ha a gép sebessége a földhöz képest 1000 km/h, akkor ez az érték hozzáadódik a Föld forgási sebességhez, ami így v = 2667 km/h = 741 m/s lesz, az ehhez tartozó centrifugális erő súly egyenértéke már 862 grammnak felel meg, utasunk súlycsökkenése ekkor már a magassággal csökkenő gravitációval együtt meghaladja az 1 kilogrammot. Ha viszont a repülő nyugat felé veszi az irányt, akkor az eredő sebesség 667 km/h = 185 m/s lesz és a centrifugális erő súly egyenértéke csak 54 grammnak felel meg. Ennek gyakorlati jelentősége is van, mert amikor az egyenlítő közelében kelet felé bocsátjuk fel az űrrakétát, akkor számottevő energiát takaríthatunk meg.

Súlyveszteség Budapesten

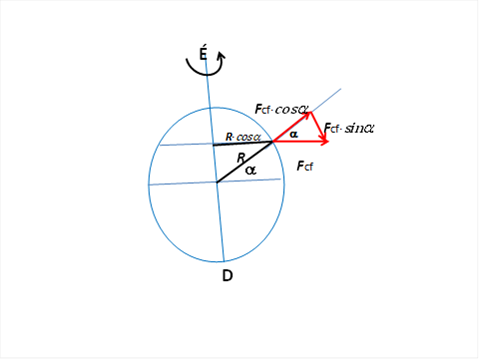
De mi a helyzet itt nálunk Budapesten? A kerületi sebesség itt kisebb, mert a körforgás sugarát a forgástengelytől kell számítani, ami a délkör pozíciójától függ. A délkör szögét alfával jelölve ez a sugár R.cosα lesz. A kerületi sebesség is ennek mértékében változik, ezért a v²/R-el arányos centrifugális erő az egyenlítőnél mért értékhez képest szintén cosα mértékében csökken. A centrifugális erő ráadásul nem is függőleges, eltérően a gravitációs erőtől, hanem α szöget zár be vele, ezért a gravitációs erővel való összegzésnél a centrifugális erő függőleges irányú vetületét kell figyelembe venni, vagyis még egyszer szorozni kell a cosα tényezővel. Emiatt lesz az erő járuléka cos²α mértékében kisebb az egyenlítőnél számolt értékhez képest. Budapest a 47⁰ délkörön fekszik, ezért a csökkenés aránya 0,465 lesz, ennek megfelelően a 100 kilós emberünk súlya 157 grammal lesz kevesebb. A centrifugális erő másik hatása, hogy a súly iránya nem lesz pontosan függőleges. A centrifugális erő vízszintes vetületét sinα  határozza meg, ezért az egyenlítői centrifugális erőt  a sinα·cosα = ½sin2α  faktorral kell szorozni. Ez déli irányú kitérést hoz létre, amelynek szöge épp Budapest környékén a legnagyobb és értéke 0,18⁰ fok lesz.

 Súlyveszteség Budapestről elrepülve

Szálljunk fel most egy repülőre Moszkva felé. Budapest magasságában a földforgás kerületi sebessége 1137 km/h, ehhez hozzávéve a gép 1000 km/h sebességét a járat teljes sebessége 2137 km/h = 594 m/s lesz és emellett még a forgási sugár is kisebb lesz: 4344 km. Ezt is számításba véve  100 kilós emberünkre ható centrifugális erő 812 grammnak felel meg lesz, de ennek iránya nem esik egybe a gravitációs erővel. Ha ennek függőleges vetületét vesszük figyelembe, akkor a súlyveszteség 546 gramm lesz, majd adjuk ehhez hozzá a 10 km magasságban bekövetkező gravitációs csökkenést, akkor együttesen 858 grammot kapunk, tehát közel egy kiló lesz a súlyveszteség. Nyugati irányba, mondjuk Párizs felé már nem érdemes utazni, ha súlycsökkenésben reménykedünk, mert ekkor a teljes sebesség csak 137 km/h lesz, amihez már nagyon kis súlycsökkenés tartozik.

A blog további írásait összefoglalja a „Paradigmaváltás a fizikában” című bejegyzés a megfelelő linkekkel együtt.