I. rész folytatása:

A kvantummechanikai oszcillátor pozíciójának valószínűségi eloszlása a kitérés függvényében 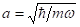 egységekben, a görbék közül az első négy (fekete: n = 0, kék n = 1, piros: n = 2, zöld n = 3) rezgési módust mutatja az ábra:

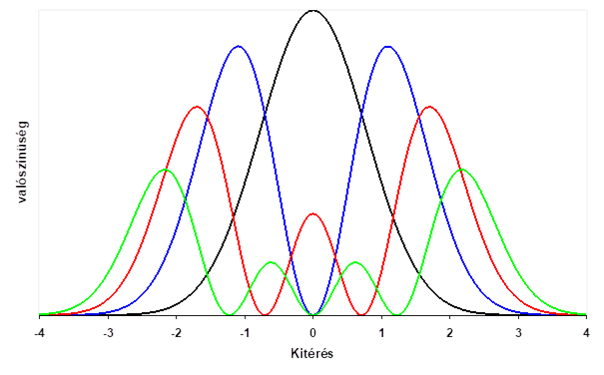
A rezgési alap módus (n = 0) egyetlen szimmetrikus haranggörbe, ahol a rezgő objektum legnagyobb valószínűséggel a centrumban található meg. Az első gerjesztett nívó, tehát n = 1 esetén két maximum figyelhető meg és a középpontban nulla a tartózkodási valószínűség. Az n = 2 és 3 esetben már három illetve négy maximum lép fel. A belső maximumok amplitúdója n növekedésével csökken és nagyon nagy n értékeknél már csak a két szélső maximum rendelkezik számottevő amplitúdóval.

 A klasszikus és kvantummechanikai oszcillátorok viszonya 

Hasonlítsuk össze a fenti kvantummechanikai képet a klasszikus modellel. Ott az x(t) kitérést írtuk le az idő periodikus függvényeként, tehát válaszolni tudunk a „hol” és a „mikor” kérdésére. A kvantummechanikában erre nincs mód, csak a tartózkodási valószínűségeket ismerjük, de arról nem tudunk semmit, hogy a rezgő objektumnak épp mekkora a pillanatnyi kitérése. Vessük fel a kérdést, hogy lehetséges-e a klasszikus oszcilláció esetén is használni a valószínűségi koncepciót? Ekkor azt kell megvizsgálni, hogy mekkora valószínűséggel találjuk meg a rezgő objektumot egy adott x kitérésnél. Ez a valószínűség a sebesség reciprokával lesz arányos. Viszont az x = ±A maximális kitérésnél a sebesség nulla, ennek reciproka végtelen, és ezért nem kaphatunk egységre normált eloszlást. Csak annyit mondhatunk, hogy a két végpontban egyenlő valószínűséggel találjuk meg a rezgő objektumot. Határesetben ehhez tart a kvantummechanikai leírás is, mert nagy n kvantumszámoknál már csak a két szélső helyzet rendelkezik jelentős valószínűséggel. Ez megfelel a korrespondancia elvnek, amely szerint nagyszámú részecske esetén, vagy nagy értékű kvantumszámmal jellemzett állapotokban, a klasszikus és a kvantummechanikai számítások azonos eredményre vezetnek. 

Az oszcillátor módusait szemléltethetjük a húr rezgéseivel is. Ha a húr két végpontja rögzített, akkor az alaphangot egy fél-hullám írja le, amikor a húr közepén maximális a kitérés. Megpendíthetjük azonban a felharmonikusokat is, az elsőnél egy teljes hullám jön létre, két szélsőértékkel és középen egy csomóponttal, a másodiknál másfél hullám alakul ki három szélsőértékkel és két csomóponttal és így tovább. A maximális kitérések száma azonos a kvantummechanikai oszcillációnál látott amplitúdó maximumok számával. A húr első három rezgési módusát illusztrálja a következő ábra.

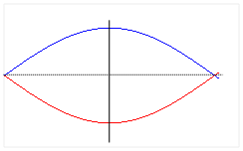
A húr rezgései és a kvantummechanikai oszcillátor közötti hasonlóság abból fakad, hogy a centrumtól nagy távolságban nullához tart a hullámfüggvény, tehát a végpontok kötöttek. A nulla végpontok között több maximum is lehet, ez felel meg az egyes módusoknak. Az első gerjesztett rezgési módus kialakulását úgy tudjuk értelmezni, hogy az alapállapotban a fény ℏ.c/ω impulzust ad át a rezgő atomnak, de az impulzus iránya a foton fázisának ismeretlensége miatt bármilyen lehet. Emiatt a rezgés is bármilyen irányban megindulhat, viszont később a középpontba visszahúzó erő hatására a kitérés csökkenni fog. Minthogy nem áll rendelkezésre információ, hogy hol és milyen irányban történik a kezdő lökés, így a kvantummechanika arra kényszerül, hogy minden lehetséges kezdő pozíciót és impulzusirányt számba vegyen és ezek átlagolásával (a várható érték kiszámításával) adja meg a végeredményt.

 A mozgás időbeli lefutásának vizsgálatára, azaz a pillanatnyi kitérés meghatározására, a klasszikus mechanikától eltérően nem kerül sor. Ehelyett csak az egyes rezgési állapotok közötti átmenetek valószínűsége határozható meg. Annak a valószínűsége, hogy a fotonokkal való rezonancia hatására a molekula vibrációs állapota az n = 0 állapotból az n = 1 kvantumállapotba gerjesztődik a következő kifejezéssel arányos:

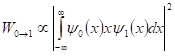
A fenti dipólus átmenet valószínűségének formulájában azért szerepel az x változó, mert a molekula vibrációs amplitúdója, illetve a molekulában a pozitív és negatív töltések súlypontjának távolsága (ez határozza meg a molekula elektronos dipólusmomentumát), kicsi a gerjesztési foton hullámhosszához képest, és ezért a foton elektromos tere állandó erővel hat a teljes vibrációs ciklus során. A teljes erőhatást viszont az x változó szerinti integrál adja meg, ami állandó erő esetén az x koordináta lesz. Az átmeneti valószínűség nullától különbözik, mert az n = 0 Hermite polinom páros, míg az n = 1 páratlan függvényt alkot, így a két függvény és az x változó szorzata páros lesz. Az integrál alatti kifejezésnek azért kell párosnak lenni, mert különben a pozitív és negatív tartománytól származó járulékok épp kioltanák egymást. Ez alapján fogalmazható meg az általános kiválasztási szabály, amely szerint az n→n±1 oszcillációs átmenet megengedett lesz. Az n→n±2  átmenet tiltott az integrálandó függvény páratlan jellege miatt, míg a n→n±3  és a további magasabb kvantumugrások az Hermite polinomok egyéb matematikai tulajdonságából következnek. Ha kisebb intenzitással is, de az n→n±2 tiltott átmenet is megfigyelhető, Ennek oka részben a rezgések nem-harmonikus jellege (a potenciál függvény nem tisztán parabolikus), illetve abból a közelítésből fakad, hogy a foton hullámhosszát végtelenül nagynak vettük a vibrációs rezgés amplitúdójához képest, de ez csak bizonyos határig igaz. Magasabb közelítésben a fenti kifejezéssel meghatározott dipólus átmenetek mellett fellépnek kvadrupólus átmenetek is.

A vibrációs állapot foton gerjesztésének valószínűsége az x koordinátától függ, és ez a gerjesztés átviszi az egyetlen haranggörbével rendelkező eloszlást a két maximummal rendelkező eloszlásba, amit a korábbi ábra szemléltet. Ennek matematikai megfogalmazása, hogy a ψ₀(x)x szorzat éppen azonos az ½ψ₁(x)  függvénnyel, azaz az átmeneti valószínűség formulája egyúttal megfelel az első gerjesztett rezgés eloszlásfüggvényének is. Másképp fogalmazva a centrumban maximális valószínűséggel rendelkező alapállapot átmegy egy olyan állapotba, ahol a centrum helyén csomópont alakul ki. A gondolatmenet kiterjeszthető a magasabb n kvantumszámhoz tartozó eloszlás függvények értelmezésére is. Ez a megállapítás is alátámasztja azt a felfogást, hogy a kvantummechanika olyan matematikai formalizmus, amely azon alapul, hogy az atomi objektumok, illetve elektronok fizikai paramétereit a fotonoktól átvett, vagy fotonoknak átadott kvantált mennyiségek (impulzus, impulzusmomentum és energia) határozzák meg. Más szóval a fotonok kvantált tulajdonságai kényszerítik ki az atomi objektumok kvantált természetét is.

Folytatás a III. részben: "Miért diszkrétek az energianívók kötött állapotban_III"

További bejegyzések összefoglalója: "Paradigmaváltás a fizikában"