Célunk annak a megértése, hogy miért kvantumosak a mikrovilág mozgásai. Az elemi objektumok (fotonok, elektronok stb.) perdületét (spin) a tér fénysebességű forgásaival értelmezhetjük, ahol a forgásokat stabilizáló erőt (erős gravitáció) az extrém nagyságú térgörbület hozza létre. Evvel magyarázni tudjuk a részecskék saját impulzusmomentumát, a spint, ami az erős gravitáció erőállandójából vezethető le és értéke fotonoknál a ħ = h/2π redukált Planck-állandó és ħ/2 az elektronoknál és más elemei fermionoknál. Viszont felvetődik a kérdés, hogy miért következik ebből a különböző atomi mozgások kvantáltsága, gondoljunk például a molekulavibrációra, vagy az atomok és molekulák elektronpályáira? A kérdés tisztázása érdekében összehasonlítjuk az oszcillátorok klasszikus fizikai és kvantummechanikai elméletét. Erre jó példa a molekulavibráció, ahol a klasszikus fizika rezgésfogalma jól alkalmazható, de bizonyos jelenségeket, például az energiaskála ekvidisztans jellegét, csak a kvantummechanika tudja értelmezni. Mivel a térelméletek (precízebben mezőelméletek), mint például a kvantumelektrodinamika, oszcillátorokból építik fel az összetett kvantumrendszereket, így az elméletek alapjainak megértéséhez is hozzásegít a kétféle szemléletmód összehasonlítása.
Klasszikus oszcillátorok
Oszcilláció jöhet létre, ha a testre ható erő valamilyen középpont felé mutat. Ennek speciális esete a Hook-törvény, amikor az erő arányos az egyensúlyi helyzettől való kitéréssel. Példa erre a molekularezgés, amikor két atomot összekötő vegyértékerő hozza létre a mozgást. Ekkor az erő x irányú változása: F(x) = –k.x és a hozzá tartozó potenciális energia V(x) = ½ k.x2. Itt a k erőállandó a molekula elektronjainak kölcsönhatásából származtatható, ennek számításával itt nem foglalkozunk, csupán a kémiai kötés erősségére jellemző állandóként kezeljük. A klasszikus fizika Newton-féle mozgásegyenletének m(d2x/dt2) = –k.x időben periodikus függvény a megoldása: x(t) = A.sin ω(t-t0) , ahol ω2=k/m.
Az oszcillátor rezgésének sajátfrekvenciája tehát megadható az erőállandó és a tömeg hányadosával és értéke nem függ a kitérés amplitúdójától. Ezt a mozgást nevezzük harmonikus rezgőmozgásnak. A rezgőmozgás energiája pedig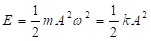
A klasszikus leírásban függvénykapcsolat áll fent az amplitúdó és az energia között, amely az amplitúdó négyzetével arányos.
Kvantummechanikai oszcillátorok
A klasszikus oszcillátor amplitúdója és ennek következtében energiája folytonosan változik, ez viszont azt jelenti, hogy a vibrációt végző atomok folytonosan és nem kvantumokban veszik fel, vagy adják le az energiát. Molekularezgések esetén elektromágneses sugárzással, azaz fotonokkal, rezonanciaszerűen adhatunk át energiát az oszcillátornak, vagy vihetünk el onnan, ez viszont megköveteli, hogy a sugárzás frekvenciája legyen egyenlő a rezgő objektum sajátfrekvenciájával. Viszont a rögzített ω frekvencia miatt a foton energiája jól meghatározott értékkel rendelkezik: Efoton = ℏ.ω. Ezért a fotonok által átadott, vagy elvitt energia (abszorpció és emisszió) is csak a fenti kvantumokban lehetséges. Az oszcillátor energiája lépcsőzetesen változik a fotonok hatására, ami ekvidisztans energiaszintekhez vezet, ahol a szeparáció ΔE = ℏ.ω lesz. Az energiaszintek ekvidisztans jellegét az sem változtatja meg, ha részecskék bombázásával, vagy molekuláris ütközésekkel közöljük az energiát, mert végső soron mindegyik folyamat elektromágneses kölcsönhatások által valósul meg, amelyet a kvantumelektrodinamika szerint valódi és virtuális (azaz közvetlenül nem megfigyelhető) fotonok közvetítenek. Ebből az következik, hogy nem azért kvantált az oszcillátor energiája, mert az atomok közötti vibráció energiája diszkrét értékeket vesz fel, hanem azért, mert az energia a fotonoktól kvantumos egységekben érkezik. Úgy is fogalmazhatunk, hogy a fotonok kvantáltsága magával hozza a molekularezgések kvantáltságát is. A kvantummechanikába pedig úgy kerül bele a kvantálás, hogy a foton ℏ.ω energiájából, illetve ℏ.ω/c impulzusából kiindulva az energia és impulzus operátorában a ℏ Planck állandó szerepel (Lásd az „Út a kvantummechanika megértéséhez” c, bejegyzést).
Nézzük meg, hogyan érvényesül ez a koncepció a kvantummechanikai tárgyalás során. Az oszcillátor Schrödinger egyenlete:

Az egyenlet megoldására standard módszerek léteznek, melynek csak néhány sarokpontját ismertetjük. Először a klasszikus A amplitúdóval rokon hosszúság dimenziójú a = négyzetgyök(ℏ/m.ω) mennyiséget és a dimenziómentes ξ = x/a változót vezetjük be, amikor is a differenciálegyenlet: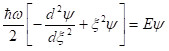
Az állandó együtthatójú differenciálegyenletek megoldásának első lépése az aszimptotikus hullámfüggvény keresése. Ez azt jelenti, hogy vizsgáljuk azt a tértartományt, ahol már nagy távolságban vagyunk a rezgés centrumától, azaz ahol a x változó nagy értéket vesz fel. Ebben a tartományban teljesül, hogy ℏ.ω.x2 >> E, ezért a differenciálegyenlet egyszerűsödik a kicsinynek tekintett E elhanyagolása miatt, amikor is a megoldás haranggörbe lesz: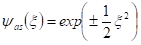
A függvényben szereplő ± előjel két megoldást kínál, melyek közül csak a negatív előjel megfelelő, mert az állapotfüggvény nem vehet fel végtelenbe futó értéket. Ekkor a rezgési centrumtól való nagy távolságban az állapotfüggvény exponenciálisan csökken. Visszatérve az eredeti x koordinátára felírhatjuk az oszcilláló atom pozíciójának valószínűségi eloszlását, melyben az a amplitúdó határozza meg a statisztikai szórást: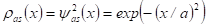
Ez az eloszlás csak nagy amplitúdóknál érvényes, az általános kifejezés egy véges tagból álló polinom és az aszimptotikus függvény szorzataként adható meg: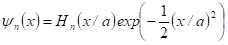
Ahol Hn(x) az un. Hermite polinom. Az n kvantumszámú állapotfüggvényhez tartozó energia pedig:
En = ℏ.ω(n + ½)
Itt az energia pozitív, mert azt vizsgáljuk, hogy a kötött objektum energiája mennyivel növekszik meg a rezgések miatt. Az energia kifejezése pontosan megfelel annak a várakozásunknak, hogy a fotonok által közölt energia ℏ.ω csomagokban érkezik, az viszont szokatlan a klasszikus oszcillátorhoz képest, hogy a legalsó állapot energiája nem nulla, hanem fele az energia kvantumának. Ez azt jelenti, hogy kötött állapotban mindenképp számolni kell a rezgésekből származó energiával bármilyen alacsony is legyen a hőmérséklet, amiben a molekulát vizsgáljuk. Ezért nevezik az n = 0 értékű vibrációt zérusponti rezgésnek.
Ennek eredete a kvantummechanikai bizonytalansági relációra vezethető vissza. A valószínűségi leírás egyik következménye, hogy egyidejűleg nem határozható meg tetszőleges pontossággal a pozíció és az impulzus. Ha az alapállapot energiája nulla lenne, akkor nem lenne mozgás, azaz a részecske a tér egy pontjához lenne rögzítve. Ez viszont a pozíció pontos meghatározását jelenti, ami megköveteli, hogy az impulzus bizonytalansága korlátlanul nagy legyen, és így végtelenül nagy lesz az energia ingadozása is. Az energia bizonytalansága a adagokban érkező, vagy távozó kvantumokhoz igazodik (tehát 0 és ℏ.ω lehet) , ezért a kvantum fele adja meg azt az átlagértéket, ami jellemzi az alapállapot energiáját. A kvantumelektrodinamikai tárgyalásban az alapállapot energiáját a virtuálisan elnyelt és kibocsátott fotonok egyensúlya határozza meg.
A kvantummechanikai oszcillátor rezgéseit leíró valószínűség eloszlási függvény:
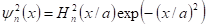
Folytatás a második részben: Miért diszkrétek az energianívók kötött állapotban_II"
A blog további bejegyzéseinek összefoglalója: "Paradigmaváltás a fizikában"




