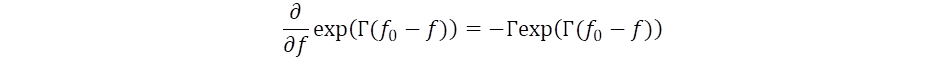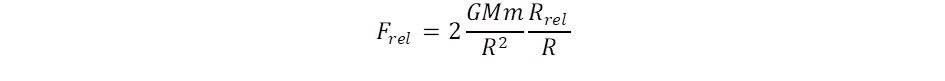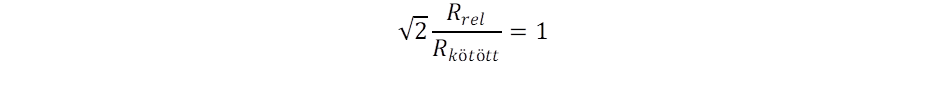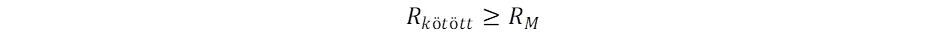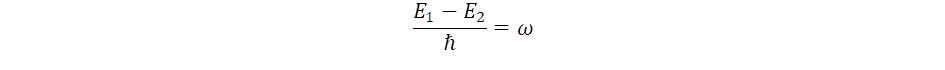Előszó:
Üres térben a fogalmak is üresek
A tér az anyag előszobája, a tér potenciális anyag
Kezdetben az idő sem létezett, az idő együtt született az univerzummal
- Bevezetés
Az ősrobbanáselmélet a jelenlegi csillagászati megfigyelések extrapolálása a távoli múltba. Azzal a hipotézissel indul, hogy az univerzum létrejöttekor egyetlen matematikai pont volt, amiben már jelen volt a világ összes energiája és anyaga. Ebből az állapotból indult el univerzumunk. melynek történetében több minden történt az első másodpercben, mint az azt követő 13,8 milliárd év során. Ez a szingularitáson alapuló hipotézis abszurd, de ha gondolatkísérletnek tekintjük, levonhatunk belőle hasznos következtetéseket, amikor olyan kérdéseket tárgyalunk, hogy mi történhet az anyaggal extrém körülmények között. Mindenekelőtt a fizika négy alapvető kölcsönhatását vizsgálhatjuk olyan körülmények között, amikor nagyságrendi különbségek alakulnak ki az erők sorrendjében. A jelenlegi kozmológia szingularitásait lenyesegetve azt nézzük meg, hogy a fennmaradó megállapítások és hipotézisek hogyan helyezhetők racionális kontextusba. Felmerülnek ontológiai kérdések is: mi értelme van térről, időről, anyagról beszélni, amíg nem jött létre univerzumunk? Átveszünk a mai kozmológiából olyan kérdéseket is, hogy hová tegyük az inflációt, az univerzum kezdeti gyors felfúvódását, mi lehetett ennek kiváltója? Keressük annak okát is, hogy miért tágul gyorsulva univerzumunk.
A mostani írásban kifejtett kozmológia alapjait korábbi könyveimben1 már kifejtettem, de több kérdésben sikerült tovább lépni. Ezért tartom érdemesnek újra összegezni kozmológiai nézeteimet.
- Elmélet
- 1. A pontszerű univerzum hipotézise
Tegyük először vizsgálat tárgyává, hogy mennyire megalapozott a hipotézis, mely szerint egyetlen matematikai pontból indult el az egész univerzum története. Ez szélsőséges extrapoláció, amely eljut egészen odáig, amikor a világegyetem egyetlen matematikai pontba szűkül le. Alapja a galaxisok távolodási törvénye. A galaxisok vöröseltolódása ugyanis arra mutat, hogy az univerzum tágul, a megfigyelések szerint minél nagyobb egy galaxis távolsága, annál nagyobb mértékű a vöröseltolódás, amit a távolsággal növekvő távolodási sebességgel értelmezhetünk. Ez a Hubble törvény, mely szerint v = H·R. Nincs alapunk azt hinni, hogy a Tejút lenne az univerzum centruma, ezért ennek a törvénynek bármelyik galaxisból nézve érvényesülni kell. Vagyis a tágulás minden irányban azonos sebességgel valósul meg. A közkeletű felfogásban ezt egy felfújható szappanbuborék szemlélteti, ahol a felület bármely két pontja azonos mértékben távolodik a felfújás során. Ezt kétféle módon képzelhetjük el: vannak pöttyök a gömb felületén, amelyek mérete is növekszik a felfújás során, de úgy is értelmezhetjük a pontokat, mint változatlan méretű molekulákat. Vajon melyik modell felel meg a galaxisok távolodásának? Mivel nincs olyan megfigyelés, ami a távolodó galaxisok növekvő méretére utalna, sőt még a James Webb űrteleszkóp legújabb felvételei is arra utalnak, hogy a rendkívül távoli, az univerzum nagyon korai szakaszából származó galaxisok – ezek az un. vörös szörnyek – szerkezete és nagysága nem különbözik lényegesen a maiaktól. Ebből az következik, hogy a galaxisok állandó méretű molekulák analógiájára viselkednek. Emiatt a jelenből visszafelé haladva oda jutunk, hogy egykor a többszáz milliárd galaxis egyetlen objektum lehetett: az ősgalaktika. Ha viszont a mozgás során állandó a galaxisok mérete, akkor miért lettek volna kisebbek az ősgalaktikát megelőző korszakban? Ha pedig állandó a galaxisok mérete, akkor az egész univerzum nagysága sem lehet ennél kisebb! Ebben a sűrű állapotban óriási a hőmérséklet, előállhatnak azok a feltételek, amikor az elektronok leszakadnak az atommagokról, és a töltések turbulens áramlása elnyeli a fényt. Innen szétáradva és lehűlve jöhetne létre az olyan univerzum, amikor már az atommagok megkötik az elektronokat, és így szabadjára engedik a fényt: útjára indulhat a mikrohullámú háttérsugárzás!
- 2. Spontán szimmetriatörés
Emiatt az univerzum történetének kiindulópontja a mai galaxisokkal összemérhető kiterjedésű plazmaállapot lehetett. Mégis izgathat minket a kérdés: mi lehetett a plazma állapot előtt? De ez már végkép a spekuláció birodalmába vezet, mert a töltések turbulens áramlása eltakarja előlünk a korábbi történéseket. Csak annyit tehetünk, hogy a mai fizika által bizonyítottnak, vagy legalábbis elfogadottnak tekintett elméleteit próbáljuk visszavetíteni. Erre példa Higgs hipotézise2, aki az elemirészecskék, a fizikai világ legparányibb objektumainak alaptulajdonságát akarta megérteni: honnan ered a tömegük? A probléma abból fakad, hogy a relativitáselmélet posztulátuma szerint minden kölcsönhatás fénysebességgel terjed. Viszont ez ütközik azzal a feltétellel, hogy tömeggel rendelkező bozonok lehessenek a közvetítők. Már pedig erre jutott a gyenge kölcsönhatás elmélete, amelyben nagytömegű W és Z bozonok közvetítik a kölcsönhatást3. Ezt a dilemmát hidalja át Higgs koncepciója, aki a spontán szimmetriatörésre vezeti vissza a tömeg eredetét. Ebben egy magas szimmetriájú metastabil állapot spontán módon átugrik egy alacsonyabb szimmetriájú és kisebb energiájú állapotba, és az energianyereség lesz forrása egy tömeggel rendelkező bozonnak, az un. Higgs bozonnak. Ez a részecske viszont gyorsan elbomlik és átadja tömegét az ismert elemi részecskéknek, a barionoknak és leptonoknak.
- 3. Metastabil szimmetria és a Higgs mechanizmus láncreakciója
De mi lehet ez az „ősi” szimmetria? A kérdésre választ kapunk, ha visszanyúlunk Einstein gravitációs felfogásához. Eszerint a tömeg maga körül görbíti a teret! Ahol nincs tömeg, ott görbület sincs, ott a tér euklideszi geometriával rendelkezik. Ennek alapja a transzlációs szimmetria: bármilyen eltolás ezt a geometriát önmagába viszi el, viszont ez megszűnik a görbületek megjelenésével. A tömeg megjelenése tehát szimmetriatörés! Az euklideszi geometria két irányban torzulhat: lehet elliptikus és lehet hiperbolikus. Vajon melyik irányban következhet be a szimmetria megtörése? Az elliptikus geometria Einstein gravitációs elmélete szerint a tömegvonzást hozza létre, ha viszont az induló geometria hiperbolikus, akkor megfordul a térgörbületek előjele, és ebben a térben már taszítják egymást a tömegek. Ezért úgy foghatjuk fel az univerzum kezdeti szétrobbanását, az ősrobbanást, hogy ezt a hiperbolikus tér létrejötte idézi elő. De egyetlen Higgs bozon nem csinál univerzumot! A spontán szimmetriatörés elindulhatott egyetlen pontból, ez felel meg az ősrobbanásnak, de az indulás még nem tartalmazta a mai univerzum teljes anyagát, ez csak egyetlen bozon lehetett. Úgy juthatunk el a galaxis méretű forró káoszhoz, ha láncreakciónak tekintjük a spontán szimmetriatörést. Miért jön létre láncreakció? Ez a görbület jellegéből fakad: egyetlen pontnak nincs görbülete, a görbület definíció szerint pontok körüli tartományt követel meg. Emiatt a szimmetriatörés végigfut a tér minden irányában a szomszédos pontokon: kialakul egy háromdimenziós láncreakció. Ennek során lépésről lépésre létrejön az univerzum teljes anyaga, teljes energiája. Ebben az ősi hiperbolikus geometriában a Higgs bozonok bomlástermékei taszítani fogják egymást, ezért útnak indul az univerzum tágulása. Ugyanakkor viszont a tömeggel rendelkező objektumok beindítják a gravitáció közvetítő mechanizmusát, az elliptikus geometriát felépítő térforgások áradását. Ezeket a lokális forgásokat neveztük el kepleronoknak. A tér kétféle mozgása, az általános tágulás és a lokális forgás összefonódik. Ezáltal az eredeti hiperbolikus geometriában fokról-fokra létrejönnek az elliptikus szigetek, az elkülönült galaktikák milliárdjai. Elindul tehát az univerzum több mint 13 milliárd éves története. A tömegtaszítási törvény szétbontja az eredeti sűrű galaktikát többszázmilliárd elemére. Ezek belsejében már elliptikus lesz a geometria, míg a galaxisok közötti tartomány továbbra is hiperbolikus marad. A fokozatosan táguló és lehűlő univerzum elliptikus tartományaiban a gravitáció összeforrasztja az atomok tömegét, ezáltal megalkotja az égitesteket, létrehozza a Tejutat és a galaxisok milliárdjait.
II.4. Az anyag dominanciája az antianyag felett4
A görbült térszerkezet kialakulásához társul egy másik választási lehetőség is, a formálódó fermionok kiralitása, ami lehet jobb, vagy balkéz szimmetriájú. A részecskék és antirészecskék különbsége abból adódik, hogy kétféle kiralitás létezik az anyagi világban. A párképződés mechanizmusa azért követeli meg, hogy a részecskék és antirészecskék mindig együtt képződjenek, mert a részecskék nélküli világnak nincsenek specifikus tulajdonságai, így nincs kiralitása sem. Ez mutatkozik meg a párképződési folyamatban, amely megőrzi az összességében nulla kiralitást. Kivétel ez alól a Higgs mechanizmus, amely nem párképződési, hanem választási folyamat két lehetőség közül. A láncreakció első lépésében létrejött Higgs bozon teszi meg ezt a választást, amivel eldönti, hogy miért válik az anyag uralkodóvá az antianyag felett. A láncreakció során létrejövő további bozonok, már az első bozon kiralitását veszik át. Ez a választás feleslegessé teszi a jelenlegi kozmológia „kannibalizációs” hipotézisét is, mely szerint a részecskék és antirészecskék felfalják egymást, és végül csak egy parányi statisztikai többlet marad fent. A jelenlegi kozmológia ugyanis nem elégszik meg annyival, hogy az univerzum egész energiáját egyetlen pontba sűríti, hanem feltételezi, hogy ennek a pontnak energiája sokszorosa volt a mai univerzumnak! Erre viszont nincs szükség a láncreakciós koncepcióban, hiszen az első bozon kiralitása már megszabja a szomszédos bozonok kiralitását is.
Az LHC kísérlet tervezése során felmerült olyan félelem is, hogy a Higgs bozon generálása nem okoz-e újabb ősrobbanást. Ettől félni nincs okunk, mert ez a kísérlet már a kialakult görbült térben kerül megvalósításra, ez már nem az univerzum terének és idejének újra alkotása.
További kérdések is felmerülnek: mi határozza meg a hiperbolikus ősgalaktika terjedelmét, és mennyi idő alatt jött létre? Mekkora lehetett a láncreakció sebessége, korlátozza ezt a fénysebesség? Szabhat-e határt valami a láncreakciónak, vagy az energia és tömeg termelése örökké tartó és ma is működő folyamat?
II.5. Szingularitásmentes kozmológia és a fizikai fogalmak születése
Olyan kozmológia kidolgozására törekszünk, ami nem ismeri a szingularitást. Ez együtt jár a végesség hipotézisével is. Megengedhető azonban az olyan matematikai szingularitás, amikor egy nullához és végtelenhez tartó kifejezést úgy szorzunk, hogy határértékben az eredmény véges lesz. A végesség azt jelenti, hogy létrejön egy véges méretű világ véges energiával, ez lesz az univerzum evolúciójának kiinduló pontja. Példaként nézzük meg a jelenlegi kozmológia egyik feltételezését, ami egy véges méretig és véges ideig tartó felfúvódásról5 szól, amit inflációnak neveznek. Ebben a folyamatban az univerzum mérete a fénysebességet nagyságrendekkel felülmúló sebességgel növekszik, mindaddig, amíg el nem ér egy kritikus méretet. A folyamat közben az univerzum energiája nem változik. Ezzel szemben a láncreakciós koncepció az energia és a velejáró tömeg növekedését tekinti alapnak, viszont nem beszél a növekedés sebességéről és idejéről. Ennek oka, hogy a tömeggel feltöltött világ létrejötte előtt mai fogalmaink sem létezhettek. Ha már léteznek tömeggel rendelkező fizikai objektumok, akkor van értelme az objektumok mozgásáról is beszélni, akkor tárgyalhatjuk a mozgást a tér és idő dimenziójában. Ettől fogva létezhet a tér és idő. Az anyagivilág és a fogalmak evolúciója összetartozik! Úgy is fogalmazhatunk, hogy a tömegnélküli, a tehetetlenségmentes euklideszi térben a görbület terjedésének sincs tehetetlensége, időbeli folyamatokról nem beszélhetünk. Az euklideszi tér csak egy matematikai absztrakció, a fizikai tér görbült, benne elliptikus és hiperbolikus tartományokkal, az elliptikus tartományok szigeteket képeznek a hiperbolikus tér tengerében.
Előszőr tehát anyagnak kell létrejönni, hogy legyen mit megfigyelni, és legalább elvben megállapítani az objektumok helyét és pozíciójuk változását. Viszont a láncreakció lezárultával megváltozik a helyzet, létrejön a hiperbolikus geometriájú induló tér, benne a Higgs bozonok bomlásával létrehozott barionok és leptonok seregével. Ebben már joggal beszélhetünk a forró és nagysűrűségi anyag turbulenciájáról, a hatalmas, de mégis véges hőmérsékletről is. Itt értelmet nyernek a relativitáselmélet fizikai fogalmai, a Lorentz transzformáció, a fénysebességi határ, az energia kovariancia törvénye, beszélhetünk a négy alapvető fizikai kölcsönhatásról, melyek tulajdonságait a modern fizikában a mértékinvariancia szabja meg.
Ismételjük meg gondolatmenetünket annak fontossága miatt! Létezik tehát egy kezdő szakasz, amikor az univerzum teljes anyaga és energiája létrejön, és az anyag dominanciája kialakul az antianyag felett. Amikor ez a szakasz lezárul, már beszélhetünk időről, térről és a relativitáselmélet törvényeiről is. Innen indíthatjuk el az univerzum tágulásának több mint 13 milliárd éves történetét. De mekkora lehetett a kezdő, nagysűrűségű univerzum mérete? Feltételezhető, hogy a jelenlegi galaxisok méretének nagyságrendjébe eshetett. A hiperbolikus geometriához rendelhetjük azt a taszító erőt, ami szétszaggatta az ősi univerzumot többszáz milliárd csillaghalmazra. Az ősi univerzum méretét néhány millió fényévre tehetjük. Mint látni fogjuk a következő pontban a Tejút centrumától 2 millió fényév távolságban vált át a gravitáció antigravitációra, ebben a nagyságrendben képzelhetjük el az ősi galaktikát, melyből a galaktikák százmilliárdjai szakadnak ki, és távolodnak el egymástól legalább néhány millió fényévnyi távolságra. Ennek felel meg, hogy a több mint 10 milliárd fényév kiterjedésű univerzumban a galaktikákat mindenütt több millió fényévnyi üres terek veszik körül.
II.6. A kölcsönhatások születése: a gravitáció és antigravitáció eredete
A kozmológiai séma ismertetése után térjünk rá a konkrét folyamatokra is. A már tömeggel feltöltött hiperbolikus térben tárgyaljuk meg a gravitációs és antigravitációs erők kérdését! Ez a két kölcsönhatás a tömegek közötti erők két arca, megjelenési formája, az egyik vonzást a másik taszítást hoz létre a tömegek között. Olyan modellt építünk fel, melyet a tér nem-inerciális mozgásaira alapozunk. Az elemirészecskék világát, az egész spinű bozonokat és a felesspinű fermionokat fénysebességű térforgások hozzák létre6. A részecskékben Planck hullámtörvénye és a tömeg-energia ekvivalencia egyesül:  Ez vezet el a spin, a perdület fogalmához. A fermionok tömege a lokális gömbforgások ω frekvenciájától függ: minél nagyobb a forgás frekvenciája, annál nagyobb a tehetetlenség. Az ω frekvencia egyúttal kijelöli a forgó objektum méretét is az ωr = c szabály miatt. A relativitáselmélet azáltal kerüli el a szingularitást, hogy a sebességfüggő tömegnövekedési törvény megtiltja, hogy a tehetetlenséggel (tömeggel) rendelkező objektumok fénysebességgel haladjanak. A tömegnövekedési törvényt terjesszük ki határértékben nulla tömegre is:
Ez vezet el a spin, a perdület fogalmához. A fermionok tömege a lokális gömbforgások ω frekvenciájától függ: minél nagyobb a forgás frekvenciája, annál nagyobb a tehetetlenség. Az ω frekvencia egyúttal kijelöli a forgó objektum méretét is az ωr = c szabály miatt. A relativitáselmélet azáltal kerüli el a szingularitást, hogy a sebességfüggő tömegnövekedési törvény megtiltja, hogy a tehetetlenséggel (tömeggel) rendelkező objektumok fénysebességgel haladjanak. A tömegnövekedési törvényt terjesszük ki határértékben nulla tömegre is:

(1)
Ebben a határesetben már a tér foroghat v = c sebességgel, mert a határértékben nulla m0 tömeget végtelenhez tartó 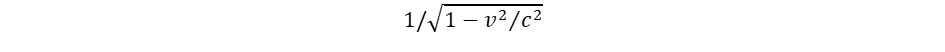 tömegnövekedéssel szorozzuk, ami már véges értéket adhat. A végesség az anyagi világ jellemzője, az anyag létformája. A tömegmentes tér csak matematikai fikció. Valamennyi bozont és fermiont fénysebességű forgás alkot, melyek a mozgások szimmetriájában és a forgások dimenziójában (egydimenziós, tengely és kétdimenziós, gömbforgás) különböznek.
tömegnövekedéssel szorozzuk, ami már véges értéket adhat. A végesség az anyagi világ jellemzője, az anyag létformája. A tömegmentes tér csak matematikai fikció. Valamennyi bozont és fermiont fénysebességű forgás alkot, melyek a mozgások szimmetriájában és a forgások dimenziójában (egydimenziós, tengely és kétdimenziós, gömbforgás) különböznek.
Itt most nem célunk a négy alapvető fizikai kölcsönhatás mezőelméletének kifejtése6, csak a gravitációra vonatkozó jellegzetességeket emeljük ki, rámutatva, hogy miben hasonlít, illetve tér el a többi kölcsönhatástól. Az elektromágneses, a gyenge és erős nukleáris kölcsönhatásnak megszületett a kvantumelmélete, amelyben a kölcsönhatások közvetítését a fénysebességgel terjedő kvantált bozonok végzik el. A kvantálás azt jelenti, hogy a közvetítő bozonok perdülete a ħ redukált Planck állandó egészszámú adagjaiból épül fel. Ezt a tulajdonságot visszavezethetjük a fénysebességű forgásokra. A felsorolt három kvantummező elmélet sikere keltette fel az igényt, hogy a gravitáció számára is kidolgozzanak kvantumelméletet. Az erőfeszítések százéves kudarca viszont arra mutat, hogy ez a törekvés hibás irányban indult el. A relativitáselmélet alapvetése szerint a gravitációhoz is szükség van fénysebességgel terjedő közvetítőre, ennek nevet is adtak, ez lenne a kvantumot hordozó graviton, de ezt nem alapozza meg konzekvens elmélet, és kísérleti bizonyíték sem támasztja alá. Hagyjuk el ezért a kvantáltság, azaz fénysebességű térforgás követelményét, és értelmezzük a gravitáció közvetítő mechanizmusát, mint a tér fénysebességnél, azaz c-nél, lassabb forgásait. Ez a forgás szintén fénysebességgel terjed, miközben úgy lassul frekvenciája és kerületi sebessége, ahogy a Kepler-Newton törvény előírja. Ennek a törvénynek sajátos vonása, hogy, amikor egy kis tömegű test kering egy nagy tömegű objektum körül, beleértve azt is, amikor a keringő test csupán a tér nulla tömegű pontja, akkor a keringési sebesség független a test m tömegétől. Eszerint a törvény szerint a sebesség négyzete arányos a centrális objektum M tömegével, és fordítva arányos a távolsággal:
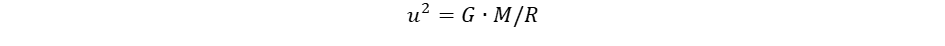 (2)
(2)
Itt G = 6,67x10ꟷ11 m3/kg·s2 az általános gravitációs állandó. Amikor nulla tömegű térpontról van szó, a keringéshez nem tartozik lendület és perdület sem, nincs ezért kitüntetett forgási tengely sem, vagyis a keringés csak gömbszimmetrikus lehet. Ezt nevezzük pont-, illetve gömbforgásnak. Ez a modell utat nyit annak megértéséhez, hogyan hoz létre a tömeg görbületet a térben az einsteini gravitációs elmélettel összhangban. A fénysebességű forgások koncepciójában a tömeget magát a fénysebességű forgás hozza létre, ahol a tömeg nagyságát a forgási frekvencia határozza meg. Ez a forgás korlátozott mértékben kiáramolhat az elemi objektumot környező térbe. A kiléptetés kiváltója három különböző tehetetlenségi erő, melyek a fénysebességgel forgó elemi tartomány belsejében működnek, mégpedig a centrifugális, a Coriolis és az Euler erő7. A belső erők kombinációja eredményezi a külső gravitációs forgás kilépését, melynek sebességét a (2) egyenlet adja meg. Emellett kiáramlanak fénysebességű tengelyforgások is, a kölcsönhatásokat közvetítő bozonok, melyek tárgyalásukra itt nem térünk ki3.
A m tömegű objektum keringését gravitációs mezőben úgy képzelhetjük el, hogy azt a tér forgása „magával ragadja”, ahhoz igazodik, mintegy együtt úszik vele. Akárcsak a Föld körül keringő űrhajóból kitett tárgyak. Ha viszont véges tömegről és így lendületről van szó, a keringés már kiválaszt egyet a tér gömbszimmetrikus forgási pályái közül, de ez a pálya már nem lesz köralakú, hanem elliptikus, melynek alakját (excentricitását) a lendület nagysága és iránya határozza meg.
A gravitáció forgó térként való értelmezése összhangban van Einstein ekvivalencia elvével, amely azonosnak tekinti a gyorsuló liftben fellépő tehetetlenségi erőt a lift alatt elhelyezkedő tömeg gravitációs erejével. Elvben a kettő megkülönbözhetetlen, ha nem látunk ki a liftből. Hasonló a helyzet, amikor az u sebességgel forgó térben kering egy m tömegű objektum, melyre mu2/R centrifugális erő hat. Ezt akkor tudja pályán tartani a vonzó erő, ha a kifelé ható erő kiegyenlítéséről az M tömegű égitest gravitációs hatása gondoskodik. Az analógia teljes, pusztán annyi a különbség, hogy a lift egyenesvonalú gyorsulása helyett a tér forgó gyorsulásáról kell beszélni.
II.7. A térforgás görbült geometriájának relativisztikus származtatása
A nem-inerciális forgó rendszerben a Lorentz kontrakció miatt nem-euklideszi geometria jön létre. Ennek oka, hogy a mozgás irányában rövidül a hosszúság dimenzió:
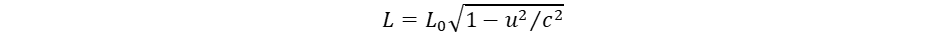 (3)
(3)
Ugyanakkor viszont a mozgásra merőlegesen nincs változás. Inerciarendszerben a Lorentz kontrakció csak látszólagos, mert nincs kitüntetett rendszer, viszont a forgásnál van, mégpedig az a rendszer, amely nem forog. Forgó rendszerben a Lorentz kontrakció miatt a kör kerülete, illetve a gömb felülete lecsökken a 2Rπ illetve 4R2π értékhez képest, miközben az R sugár változatlan marad. Ez az arány szolgál mércéül a radiális görbület jellemzésére8:
 (4)
(4)
A definíciót úgy választottuk meg, hogy a görbület nulla legyen, ha nincs forgás, egyébként pedig pozitív a görbület az elliptikus geometriának megfelelően. A görbület definícióját fordítva is megadhatjuk, amikor a számlálót és nevezőt felcseréljük. Hamarosan látni fogjuk, hogy miért éppen a (4) szerinti definíció a helyes. A (3) egyenletnek megfelelő radiális görbület:
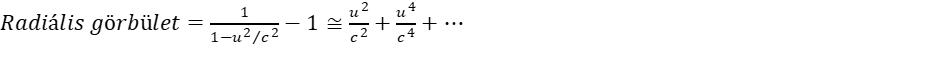 (5)
(5)
Itt a sorfejtéses kifejezés első két tagját vettük figyelembe, ami annak felel meg, hogy a Kepler sebesség kicsi a fénysebességhez képest. A görbületből számíthatjuk ki az m tömegre ható potenciális energiát, mert amikor görbült térbe kerül egy fizikai objektum, az eredeti mc2 nyugalmi energia megváltozik, mégpedig arányosan a görbülettel:
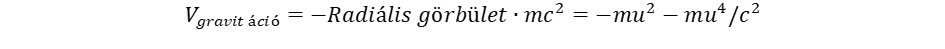 (6)
(6)
A potenciális energia konvenciójának megfelelően negatív előjelet választottunk. A potenciális energia kifejezésébe helyettesítsük be u2-et a (2) egyenletből, és képezzük a negatív gradienst a gravitációs erő meghatározásához:
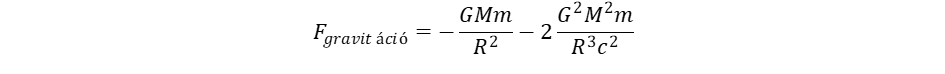 (7)
(7)
Ami rendkívül figyelemreméltó, hogy a Kepler törvényből levezetett gravitációs erő nemcsak a Newton egyenletet reprodukálja, hanem számot ad a Schwarzschild által az Einstein egyenletből származtatott relativisztikus járulékról is, ami vitathatatlanná teszi, hogy helyes a gravitáció térforgásra való visszavezetése.
Az (5)-ben megadott radiális görbület összhangban van azzal a felfogással is, hogy a fénysebességű forgás hozza létre a tömeget, mégpedig azáltal, hogy a határértékben nulla m0 tömegből véges m tömeg jön létre, amiatt, hogy a görbület határértékben végtelen, amit a tér nulla határértékű tömegével szorozva ̶-mc2 potenciális energiát kapunk. Ez pedig ellentételezi az mc2 nyugalmi energiát, ami voltaképpen a fénysebességű forgás kinetikus energiája. Az erők szintjén ez azt jelenti, hogy a fénysebességű forgás centrifugális erejét kiegyenlíti a tér térgörbületének visszahúzó ereje. Ezt úgy is megfogalmazhatjuk, hogy az elemi fermion a tér önmagát stabilizáló fénysebességű forgása. Felvethetjük a kérdést a Higgs koncepció jegyében is. A transzlációs szimmetria lokális megtörése a létrejövő m tömeg számára –mc2 energianyereséget jelent, ami forrást biztosít az mc2 kinetikus energia számára.
A radiális görbületre megadhatnánk olyan definíciót is, ahol (4) egyenletében a számlálót és nevezőt felcseréljük, de ekkor csak a Newton erőt tudnánk reprodukálni a relativisztikus korrekció nélkül. Ismeretes, hogy a Merkur pálya anomális perihéliumát épp a relativisztikus korrekció tudja magyarázni. Ezért a fenti (4)-es összefüggés tekinthető a radiális görbület korrekt definíciójának, és nem annak fordítottja.
II.8. Szinre lép az antigravitáció
A Kepler törvénynek megfelelő sebességű térforgás tehát relativisztikus leírást ad az M tömeg által létrehozott gravitációs vonzásra. A gravitációs vonzóerő távolságfüggését megfogalmazhatjuk mezőelméleti keretek között is. Ebben a leírási módban kulcsszerepet játszanak a közvetítő objektumok, amit kepleronnak és nem gravitonnak nevezünk. Az új elnevezést az teszi szükségessé, hogy nem kvantumos a közvetítés, eltérően a kvantum mezőelméletek bozonjaitól (fotonok az elektromágnesességnél, W és Z bozonok a gyenge kölcsönhatásnál, vagy a gluonok az erős kölcsönhatásnál). A kepleron azáltal hoz létre kontaktust két tömeggel rendelkező objektum között, hogy a tömegek gömbszimmetrikus térforgások bocsátanak ki, ahol a forgások kerületi sebessége nem érheti el c-ét. Ezek a forgások fénysebességgel terjednek, és intenzitásuk a gömbfelület növekedésével csökken, annak megfelelően, ahogy az egységnyi területre eső erővonalak száma változik:
 (8)
(8)
Az így definiált intenzitást –mc2-tel szorozva jutunk el a Newton által bevezetett klasszikus gravitációs erőhöz. Ennek relativisztikus korrekciójához is eljutunk, ha számításba vesszük a relativisztikus tömegnövekedést az (1) egyenletben, és figyelembe vesszük a tehetetlen és gravitáló tömeg ekvivalenciáját9.
A kepleron intenzitás és ezen keresztül a gravitációs erő arányos az objektum teljes tömegével, ez az arányosság voltaképpen az egyes atomok vonzó erejének addíciós szabálya: amely úgy jön létre a makroszkopikus objektumokban, hogy minden egyes atom pozíciójától függetlenül, tömegével arányos járulékot ad. Ez távolról sem triviális, hiszen a távolabbi atom vonzó hatása a távolság négyzetével arányosan csökken, vagyis kisebb az erő, mint amit a közelebbi objektumok létrehoznak. Gömbszimmetrikus objektumokban, legyen szó bolygókról, vagy csillagokról, bármely kiválasztott pontból nézve az atomok száma a távolság négyzetével nő, ami épp kiegyenlíti a távolsággal csökkenő erőt, ezért például a Föld felületén állva, vagy afelett keringve, ugyanakkora erő hat ránk, mintha az egész tömeg a Föld centrumában lenne. Ezt a szabályt eredetileg még Newton állapította meg. Az einsteini képben a tér görbületi adatai összegződnek, amit a gömbforgások szuperpozíciójaként értelmezünk. A makroszkopikus térgörbületet az egyes atomok adják össze, melyek 10–10m távolsága rendkívül kicsi a csillagászati méretekhez képest, és így távolság szerinti megkülönböztetésük nem indokolt.
Két csillaghalmaz közötti erőhatás számításánál abból kell kiindulni, hogy a gravitáció összegzési szabálya nem működik a többi galaxistól való nagy távolság miatt, vagyis itt már galaxis méretű kepleronok közvetítik a kölcsönhatást. Ezek távolságfüggő intenzitását a (8) összefüggés adja meg, és figyelembe kell venni, hogy a nagy távolság megtétele miatt a kepleronok átalakulnak. Mi okozza ezt az átalakulást?
Ennek megértése kedvéért szóljunk még a térforgásokról szerezhető információ természetéről. Eddig a tér egyik gömbszimmetrikus gyorsuló mozgásáról beszéltünk: a pont körüli forgásról. Létezik azonban egy másik is: a tér tágulása, melynek sebessége arányosan növekszik a távolsággal. Megfigyelni csakis a tömeggel rendelkező fizikai objektumokat tudjuk, viszont a tér pontjait nem láthatjuk, hiszen ezek nem bocsátanak ki fotonokat. Vizsgálhatjuk azonban a galaxisokból érkező fény hullámhosszát, melynek változásából következtetünk a tér tágulására. A tér tágulásának nincs kitüntetett centruma, bármely pont körül azonos a tágulási kép. Erről szerzett információnk tehát indirekt. Szintén indirekt információt használ a kvantummechanika, amikor az elektronpályát nem időben egymásutáni pozíciók sorával írja le, hanem arról beszél, hogy milyen az elektronok eloszlásának valószínűségi térképe. Amikor a tér mozgásáról beszélünk, akkor a térpontok által leírt lehetséges pályákat vesszük sorba, nem pedig a térpontok időben egymást követő helyzetét, ezért ekkor is csak valószínűségi kijelentéseket tehetünk. Helyesebb ezért a térforgásokat és a tágulást nem pályaként fefogni, hanem a kvantummechanikai megfogalmazás mintájára a forgás illetve tágulás állapotaként. A pontforgás például azt jelenti, hogy nincs kitüntetett forgási tengely, mindegyiknek azonos a valószínűsége, vagyis a tér pontjai egy gömbfelületet futnak be. A tágulás sem valamilyen kitüntetett irányban megy végbe, hanem az összes lehetséges irányt kell számba venni. A két említett mozgásforma egymás tükörképe: a tágulás a gömb sugara mentén halad, a pontforgás viszont a gömb felületén fut végig. A speciális relativitáselmélet Lorentz kontrakciója ad ennek jelentőséget: a pontforgás lecsökkenti a felületet a sugár állandósága mellett, a tágulás a sugarat csökkenti, míg a felület állandó marad. Emiatt a felület aránya az átmérő négyzetéhez viszonyítva a pontforgás esetén kisebb lesz, mint π, szemben a tágulással, ahol az arány nagyobb lesz π értékénél. Ezzel eljutunk a kétféle nem-euklideszi geometriához: a pontforgás az elliptikus geometriát alkotja meg, a tágulás viszont a hiperbolikus geometriát.
A tér tágulását a Hubble féle tágulási törvény írja le, mely szerint az R távolságú galaxis v = H·R sebességgel (H = 70 (km/s)/Mpc = 2,3·10ꟷ181/s) távolodik tőlünk. A tágulás által okozott görbület (4) szerint:
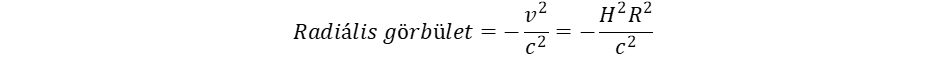 (9)
(9)
Az egyes atomok által kibocsátott kepleronok hatása összeadódik, ez tükröződik abban, hogy arányosságot találunk a tehetetlen és a gravitáló tömeg között. A gravitációs összeadódási szabálynak azonban korlátja van: ha nagy a távolság, akkor a taszító hatás már ellensúlyozza a vonzást. Ezt fejezi ki az (5) és (9) görbületek összevetése. A forgás kerületi sebessége csökken a távolsággal a Kepler törvény szerint, ugyanakkor viszont a tágulási sebesség nő, ezért ha kiindulunk a Tejút centrumából, el fogjuk érni a határt, ahol a két sebesség megegyezik:
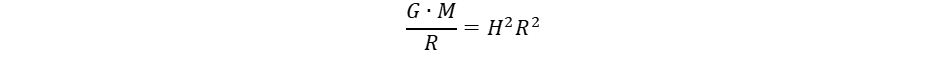 (10)
(10)
Ez adja meg az inverziós távolságot, ahol a gravitáció már antigravitációba megy át:
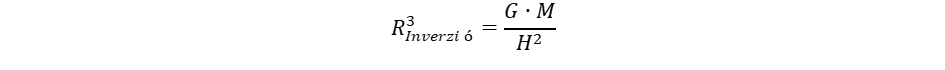 (11)
(11)
Az inverziós határon belül érvényes a gravitációs erő addíciós szabálya, vagyis az egyes atomok által kibocsátott térforgások sebessége a (2) egyenlet szerint növekszik a tehetetlen tömeg függvényében. Ez a szabály az atomoktól kezdve érvényes a csillagászati objektumokig. Az inverziós sugár Hidrogén atom esetében 20 cm, mivel a Tejútban még az interstelláris terekben is jelentős a Hidrogén atomok és ionok száma így az egész Tejút gravitációsan összekötött csillagászati objektum. Ez vonatkozik a csillagokra számítható inverziós távolságra is, ami szintén nagyobb, mint az egyes csillagokat elválasztó távolság. De mi a helyzet a Tejút egészére? Itt is jóval nagyobb inverziós távolságnak kell lenni, mint a galaktika kiterjedése, hiszen máskülönben nem adódik össze a gravitáció az antigravitáció ellenirányú hatása miatt. De így van-e? A kérdésre választ kapunk a Tejút tömegének segítségével. Ez a tömeg a csillagok fényessége alapján számítva 0,33·1042kg, amit alapul véve az inverziós távolság 2 millió fényév! Itt a sötét anyag járulékát nem vettük számításba, ezzel együtt 3,26 milliónfényév adódna ki, de az antigravitációs elv szerint sötét anyag feltételezése nem indokolt. Az inverziós távolság tehát jócskán meghaladja a Tejút méretét, melynek átmérője 100 000 fényév alatt marad, vagyis a gravitációs összegzési szabály teljesül. Ez tekinthető az antigravitációs elv kvantitatív bizonyítékának. Arra is választ kapunk, hogy miért nagyobb a távolság a galaxisok között 2 millió fényévnél. Például a Tejút legközelebbi szomszédja az Androméda 2,5 millió fényévre van. A két galaxis egymáshoz közeledik, vagyis nem érvényesül rájuk a Hubble szabály. Ekkora távolságban még nem alakul ki jelentős taszítás a galaxisok között, mert épp csak átfordul a vonzás taszításba. Kepleronokkal megfogalmazva elmondhatjuk, hogy az egyes atomok által kibocsátott térforgások összeadódnak, és megalkotnak egy gigantikus kepleront, amit a Tejút kibocsát az intergalaktikus térbe. Ezek lesznek a galaxisok közötti kölcsönhatás közvetítői. A különböző galaktikák távolsága már kívül esik a galaxis vonzáskörzetén, vagyis a vonzás átfordul taszításba.
Számítsuk ki konkrétan, hogy kiválasztva két galaktikát a többszáz milliárdból, mekkora erővel taszíthatják egymást? Amíg a galaxison belül a gravitációs összegzési szabály érvényesül, megváltozik a helyzet, amikor a különböző galaxisok közötti erőről beszélünk. Ennek meghatározásához alapul kell venni az M1 tömegű galaktikából elinduló gigantikus méretű kepleronok intenzitását a (8) összefüggés szerint. Ez az összefüggés az erővonalak intenzitását adja meg, ha energiát számolunk, akkor az integrált intenzitást, vagyis a G·M1/Rc2 faktort kell használni. Ezt kell szorozni a kölcsönhatást közvetítő kepleronok által okozott helyi görbülettel a (9) egyenletből, és az M2c2 energiával:
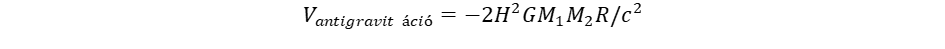 (12)
(12)
Itt még belépett egy kettes faktor is, mert egyrészt az M1 tömeg kepleronjai hatnak M2-re, másrészt az M2-é M1-re. Az antigravitációs potenciálból a negatív gradiens képzésével jutunk el az antigravitációs erőhöz:
 (13)
(13)
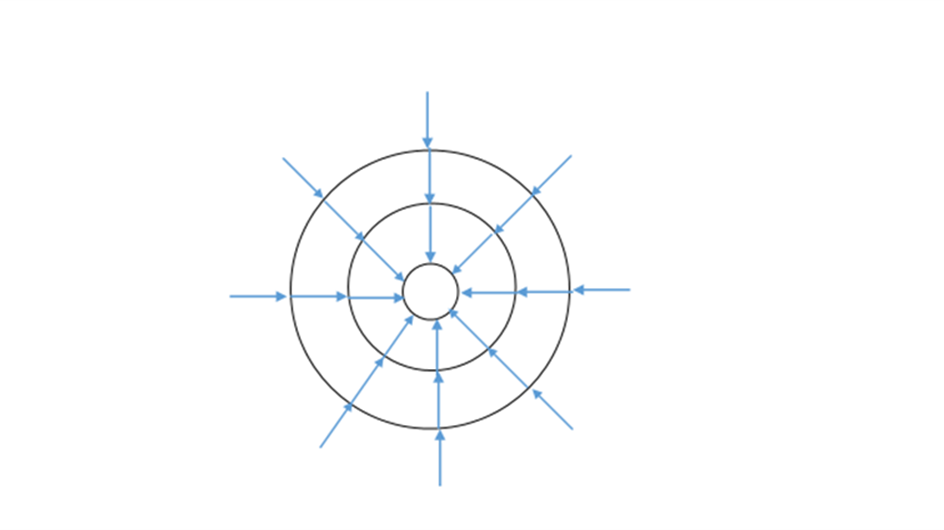
Ez akkor érvényes, ha a két galaxis távolsága nagyobb az inverziós távolságnál. Itt az erő pozitív, ez felel meg a taszításnak, és nagysága nem függ a távolságtól, tehát az univerzum bármely két galaxisa között antigravitációs taszítás lép fel, ha távolságuk eléri a néhány millió fényévet. Az intergalaktikus üres térben mindenütt azonos az antigravitációs erő, ami arra vezethető vissza, hogy az egyedi kepleronok által kiváltott R2 szerint növekvő görbületet kiegyenlíti az intenzitás R2-tel arányos csökkenése. Az univerzum szerkezete úgy alakul ki, hogy kialakul a hatalmas üres tér hiperbolikus görbülettel, amely összeszorítja a benne levő galaxisok elliptikus szigeteit.
A galaxisokat szétrepítő és összeszorító antigravitációs erőben az egész belátható univerzum kollektív hatása mutatkozik meg, minthogy az antigravitációs erő nem csökken a távolsággal (13) szerint. Itt a beláthatóságnak fontos szerepe van, mert a jelenlegi kozmológiai modell szerint jóval nagyobb az univerzum sugara 13,8 milliárd fényévnél, a teljes sugarat 93 milliárd fényévre teszik. Mivel a kölcsönhatás fénysebességgel terjed, a jelent meghatározó erőben csak a 13,8 milliárd fényéves tartományt kell figyelembe venni, de az univerzum történetében a teljes kiterjedés játszik szerepet.
Konklúzió
III.1. Topológia és antigravitáció: az univerzum szerkezetének rendező elvei
Mi történik, ha egy egyenest, egy síkot, vagy az euklideszi teret behajlítjuk? Lehetséges-e, hogy csak egyirányban történjen meg? Akkor igen, ha csak egyetlen görbületi szélsőérték létezik. Erre lehet példa az ősrobbanás pillanata. Az ősgalaxis szétszakadása azonban többszáz milliárd csillaghalmazt hozott létre, ezek mint szigetek emelkednek ki a hiperbolikus óceánból. A kétféle görbület hatással van egymásra. Induljunk ki egy galaxisból, például a Tejútból. Ez teljes egészében az inverziós határ belsejében van, ezért úgy fogjuk fel a helyi pozitív görbületet, mint a galaxis struktúráját egybekötő erőt. Ha a galaxis környezetét nézzük, akkor az univerzum nagyjából minden irányban hasonló struktúrájú, ezért minden irányból érkezik a (13) egyenlettel megadott taszító erő. Viszont a szemközti irányból érkező erők összege többé-kevésbé kiegyenlíti egymást, még ha ez a kiegyenlítés nem is tökéletes. Erről tanúskodik, hogy lehet olyan irány, ahol nagy a különbség, és ahonnan jókora lökés érkezik a kiválasztott galaxisra. Emiatt lehet jelentős eltéréseket észlelni a Hubble szabály alól. Példa rá, hogy az Androméda közeledik a Tejúthoz, de megfigyeltek más galaktikus mozgásokat is, ahol egyes csillaghalmazok nagy sebességgel közelednek egymás felé. Egy ilyen jelenség vezetett a Nagy Vonzó hipotézisére, amely szerint, létezne egy millió Tejút méretű megfigyelhetetlen csoportosulás10, amely hatalmas tömegével rántja maga felé a Tejút környezetét. Nincs azonban szükség erre a hipotézisre, mert a nagy sebesség betudható a galaxiseloszlás inhomogenitásának is.
A taszító erő sem egyenletesen érkezik minden irányból, ami forgásba hozza a galaxisokat. Ez okozza a Tejút forgását is, ami létrehozza a spirális karokat. Ilyen alakzat azért alakulhat ki, mert a Tejút centrumától kifelé haladva a csillagok keringési sebessége lényegében azonos, ami lehetővé, hogy a szomszédos keringési pályák csillagjai összekapaszkodjanak, viszont így is fokozatosan lemaradnak a nagyobb sugarú pályán keringő csillagok. A Newton törvény szerint a külső pályákon lassabb lenne a keringés, és így a csillagvonulatok nem kapcsolódnának össze, hanem szétszakadnának gyűrűk megformálásával, annak mintájára, ahogy a Jupitert és a Szaturnuszt gyűrűk serege veszi körül.
A Tejút csillagjainak azonos keringési sebessége kézenfekvő módon magyarázható a kívülről érkező antigravitációs erő dominanciájával. Ez a taszító erő közel konstans a Tejúton belül, amiért a struktúrára gyakorolt forgató nyomaték a centrumtól való távolsággal lesz arányos, ami pedig a forgató kar hosszával arányos perdületet hoz létre a keringő csillagok számára. Ebből már következik, hogy a keringési sebesség azonos lesz. Összevetve ezt a sötét anyagon alapuló képpel a különbség szembetűnő: ott a hipotézis hipotézisére kényszerülnek, amikor a megfoghatatlan sötét anyag semmivel nem indokolható specifikus eloszlását tételezik fel.
A Tejút szerkezete további példákkal támasztja alá az antigravitációs kompresszió létezését. A kívülről körkörösen érkező antigravitációs taszítás összepréseli a Tejutat, ezért kiterjedése jóval kisebb, mint amekkora indokolt lenne a gravitációs vonzás alapján. Az inverziós határ közelében levő anyagot a kompresszió gyakorlatilag „besöpri” a galaxis belsejébe. Az ebből kimaradó csillagok alkotják a galaxist környező halót. A jelenlegi kozmológia a külső préshatás helyett a sötét anyag dominanciájáról beszél, hipotézisük szerint a sötét anyag mennyisége hat-hétszer haladja meg a láthatót. Ezzel állítható szembe az univerzum összes galaxisának antigravitációs hatása, mely szerint a körkörösen érkező külső nyomás egészíti ki a centrumfelé húzó gravitációserőt, és a kettő együtt tarja keringési pályán a csillagokat. Komoly többlete ennek a koncepciónak, hogy világossá teszi, miért jön létre egy gömbhalmaz és egy rúd alakú csillageloszlás a Tejút centrumában. A Tejút centrumában már a gravitációs erő dominál a kompresszióhoz képest, és ez alakítja ki a csillagok eloszlását. Más a helyzet a széleken a külső forgatónyomaték domináns hatása miatt. Itt már lapos a Tejút szerkezete, mert a forgási síkban a centrifugális erő ellentart a külső préshatásnak, szemben a síkra merőlegesen, ahol csak a kompresszió érvényesül.
Az egyes galaxisok környezete más és más az univerzumban, ez okozza a galaktikák sokféleségét. Bár a spirálgalaxisok leggyakoribbak, léteznek eltérő struktúrájú csillaghalmazok is, ezek sokfélesége árulkodik a lokális kompresszió és forgatónyomaték változatos viszonyairól.
Az univerzum görbületi viszonyai is hatnak egymásra. A gravitációs és antigravitációs erők egymást erősítik az elliptikus tartományban, ezért az erőt létrehozó térgörbületek is helyileg összeadódna: A külső prés megnöveli a belső görbületet is. De belép még a topológiai elv is: ha valahol erősebb lesz a pozitív görbület, akkor körülötte megemelkedik a negatív görbület is. Beindul ezáltal egy pozitív visszacsatolást a két görbületi struktúra között: az antigravitációs kompresszió miatt megnövelt pozitív görbület nagyobb negatív görbületet indukál, ami viszont még jobban összepréseli a pozitív görbületű galaxisokat. Ennek a következménye lehet, hogy az univerzum gyorsulva tágul.
Ehhez kapcsolódik a gravitációs lencsehatás intenzitása is: azért lesz a vártnál nagyobb, mert a külső préshatás „összegyűri” a galaktikákat, ahhoz képest, mintha csak a gravitációs erő hozná létre a görbületeket. Ez is összhangban van a megfigyelésekkel. Az összepréselt galaxis halmazok sűrűségtérképe is megváltozik, visszaigazolva Zwicky megfigyelését a Coma klaszterben, ahonnan eredetileg elindult a sötét anyag hipotézise. Sorra véve a sötét anyag hipotézist alátámasztó érveket, az antigravitációs elv valamennyi esetben legalább olyan jó magyarázatot kínál, de vannak olyan csillagászati jelenségek is, amire egyedül az antigravitációs elv képes magyarázatot adni.
III.2. Honnan származik a sötét energia?
Az előző pontban több példán keresztül mutattuk be, hogy az antigravitáció mennyivel kézenfekvőbb magyarázatot ad csillagászati jelenségekre, mint a sötét anyag hipotézise. A Lambda CDM modell másik alapfelvetése a Lambdával jellemzett sötét energia. Ez az univerzumban mindenütt jelenlevő és a tágulást okozó energia, amely összegezi a szétáradó galaxisok mozgási energiáját, illetve annak okát fogalmazza meg egy különleges potenciális energia formájában. Az antigravitációs elmélet fontos sikere, hogy egyrészt helyettesíti a sötét anyagot, másrészt magyarázatot nyújt a sötétenergia eredetére is. Tehát elegendő egyetlen hipotézis a mai kozmológia két különböző alapfeltevése helyett.
Mi a sötét energia? Valamennyi erőfeszítés kudarcot vallott, hogy erre a kérdésre választ adjon, nem úgy az antigravitációs hipotézis. Ennek alapja, hogy az antigravitációs taszítás nem szűnik meg a távolsággal, bármekkora is legyen az. Ez az erő bejárja az egész univerzumot. Többszáz milliárd galaktika létezik, de csak a közeli szomszédok között nem lép fel taszítás. Az erő munkavégző képessége a megtett elmozdítással arányos, és ennek hossza az univerzum teljes kiterjedése! Ez a kiterjedés pedig nem csak a 13,8 milliárd fényév, hanem a Lambda CDM modell szerint 93 milliárd. Bár két kiválasztott galaxis között gyenge a taszító erő, de a nagyszámú objektum és az elmozdítás hatalmas mérete miatt a létrejövő energia óriási lesz. Ez fejeződik ki a mai kozmológiában, mely szerint a sötét energia képezi a teljes energia 65-70 százalékát. Ha összegezzük a (12)-ben megadott antigravitációs energiát, akkor a teljes univerzumra számított energia kétszeresét kapjuk, ha R = 13,8 milliárd fényév, ha azonban 93 milliárd, akkor az antigravitációs energia 13,5-ször nagyobb a láthatónál. Ez pontosan megfelel a Lambda CDM modell számításainak, ahol 5 százalék a látható anyag energiája a sötét energia 65 százalékos értékével szemben.
III.3. Tanulság
A magamnak feltett eredeti kérdés csak annyi volt, hogy magyarázatot kapjak az elektron spin eredetére, hogy honnan származik a részecske perdülete? A válasz keresése azonban sokkal messzebb vitt, egészen a kozmológia alapkérdéseihez. Nem az a fontos, hogy honnan indulunk el, hanem az, hogy bejárjuk az egész utat.
Hivatkozások a korábbi könyvekre
- A kozmosz rejtélyei. Létezik-e sötét anyag és sötét energia? Miért dominál az anyag az antianyag felett?, Scolar Kiadó, 2024
- Útikalauz a fizikához Newtontól Higgsig, Scolar Kiadó, 2020, pp. 157-158
- A kvantummechanikán innen és túl, Scolar Kiadó, 2017, pp. 159-167
- Az V. fejezet 1.-ben
- 60-69 2.-ben
- Mikrovilág misztikumok nélkül, Scolar Kiadó, 2022, IV. fejezet
- 126-127 2.-ben
- Az 1. könyv 45. oldalán a III. 14 formula a reciprok arányt adja meg, amit a mostani elemzésben megfordítottunk, hogy megkapjuk közvetlenül a relativisztikus korrekciót
- 49-50 az 1.-ban
- 99-100 az 1.-ban

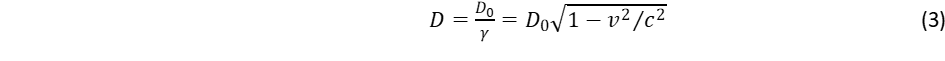
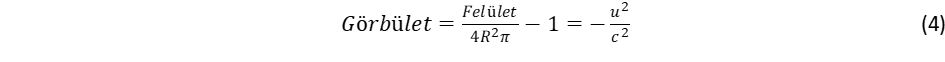
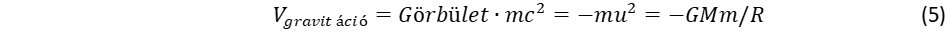
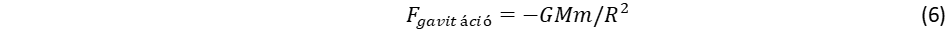
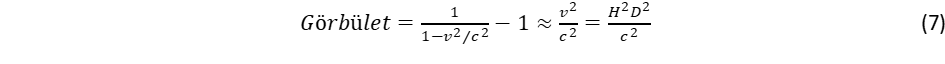



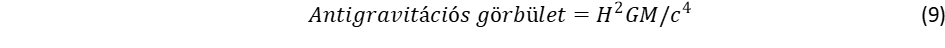
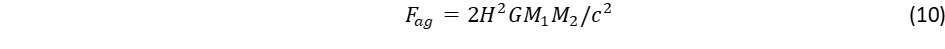

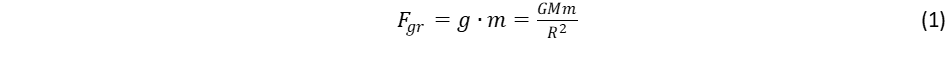

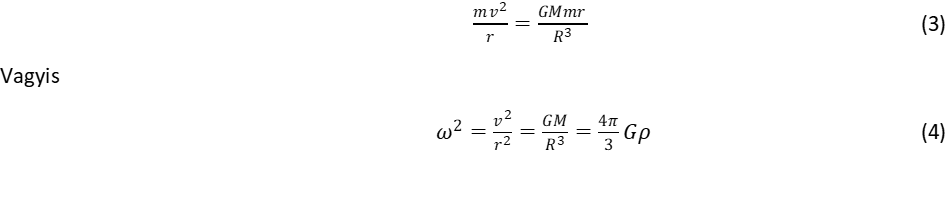

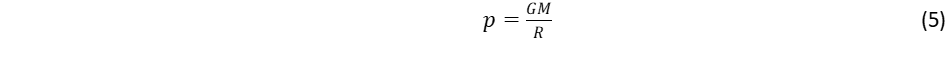

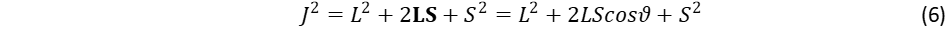
 (1)
(1)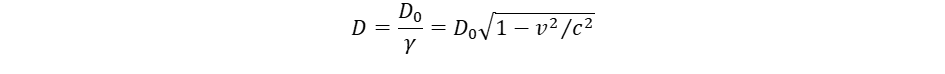 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) ___________________________________________________________________________________
___________________________________________________________________________________ (8)
(8) (9)
(9) (10)
(10) (11)
(11)

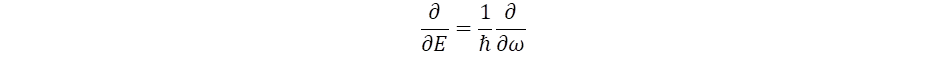 differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva:
differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva: