Fekete lyukak és a téridő szingularitása
Amikor kozmológiai kérdésekről van szó, feltétlenül beszélni kell a fekete lyukakról is, ami természetesen nem tévesztendő össze a sötét anyaggal! Einstein általános gravitációs elméletének egyik izgalmas következménye a fekete lyukak létezése, amit később – eltérően a sötét anyagtól – különböző csillagászati adatok, valamint a gravitációs hullámok megfigyelése fényesen igazolt. De valóban csak Einstein elméletéből következik, hogy léteznek fekete lyukak?
A kérdés megválaszolását kezdjük Newton gravitációs egyenletével, majd a következő lépésben vegyük figyelembe a III.11 pontban tárgyalt relativisztikus korrekciót! Ha a bolygó tömege nagyon kicsi a Naphoz képest és körpályákra szorítkozunk, akkor a centrifugális erőt egyensúlyban tartó gravitációs erő:

Az egyenlet egyik oldalán szerepel a tehetetlen tömeg, a másikon a gravitáló tömeg. A kettő egyenlősége miatt az egyenlőségből az m tömeg kiesik, és azt kapjuk, hogy

A sebességet meghatározó összefüggés érvényes, bármilyen kicsi is a keringő tömeg, vonatkozik ez a fényre is, annál is inkább, mert az m = E/c2 összefüggés szerint a fotonhoz is rendelhető fiktív tömeg. A foton viszont c fénysebességgel mozog, ezért akkor kerül „kötött” pályára az M tömeg körül, ha

Ezzel eljutottunk a gravitációs fénycsapdázás feltételéhez, amely szerint az egyenlőség alapján fogalmazhatjuk meg a fekete lyuk létrejöttének kritériumát. Ez a sugár összevethető az általános relativitáselmélet eseményhorizontjával, amely a Schwarzschild metrika szerint a 2Rrel értéknél szingularitást hoz létre. A szingularitás azt jelenti, hogy végtelen sűrűségű lenne az anyag a fekete lyuk belsejében, és a téridő szerkezetében megszakadna a folytonosság.
Ezzel eljutottunk a fizika egyik alapkérdéséhez: vajon csak valamilyen matematikai műtermék ez a szingularitás, vagy fizikai világunk egy különös jelensége? A probléma feloldására komoly erőfeszítések történtek, megpróbálkoztak a Schwarzschild megoldástól eltérő modellekkel is, mások a gravitáció kvantumos alapokra helyezését célozták meg. További törekvések különböző típusú szingularitásokat különböztetnek meg. Az utóbbi jeles képviselője Roger Penrose (1931- ), angol matematikus, fizikus és filozófus, aki a szingularitási elv megfogalmazásáért 2020-ban Nobel Díjban is részesült. Ez az elv kapcsolatot teremt a szingularitás és a fekete lyuk kialakulása között. Az elv másik kidolgozója Stephen Hawking angol elméleti fizikus is (1942-2018), aki a díj odaítélését már nem élhette meg.
A kepleron elv és a fekete lyukak
Könyvünk a kepleron modell alapján veti fel a fekete lyukak kérdését. Kiindulási pontunk a (III.22) összefüggés, amelyben az Rrel/R arány mutatja meg, hogy milyen mértékben növekszik meg a potenciális energia a relativisztikus korrekció miatt. Az erő kifejezéséhez a negatív gradiens képzésével jutunk el:
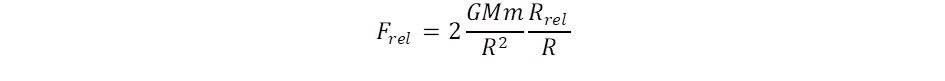
Innen látszik, hogy abban a tartományban, ahol R < Rrel a relativisztikus korrekció már meghaladja a klasszikus Newton féle erőt. Mi lesz ennek következménye a fény csapdázása szempontjából, vajon más feltételek között valósul meg? Nézzük azt az esetet, amikor az mc2/R centrifugális erőt dominánsan a relativisztikus gravitáció ellensúlyozza!

Eszerint annál az Rkötött sugárnál kerül sor a fény csapdázásra, ahol
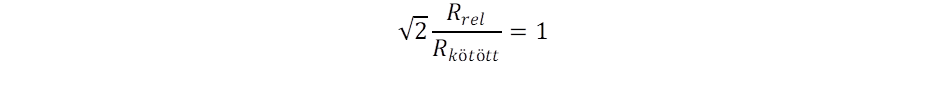
Ebből viszont az következik, hogy a relativisztikus hatás lényegében nem változtatja meg a kötött pálya kialakulásának feltételét, csupán kismértékben megnöveli annak sugarát. Ha azt az esetet nézzük, amikor épp egyenlő a klasszikus és relativisztikus gravitáció hatása, éppen eljutunk a relativitáselméletben a Schwarzschild által számított 2Rrel szingularitási sugárhoz.
A kepleron koncepcióban is az a főkérdés, hogy mi történik, amikor teljesül a fény csapdázásának feltétele. Ekkor a nulla tömegű fény zárt pályára kerül. De ezzel együtt végzi forgását maga a tér is, amely részecskévé formálódik, ha a mozgási sebesség c. A kepleron, amíg a keringési sebesség nem éri el a fénysebességét, még nem valódi részecske, nem tartozik hozzá lendület és perdület sem, de elérve a kritikus határt, már tömegről is beszélhetünk. Ennek oka, hogy a fénysebességű forgás akkor vezet el a tömeg megformálásához, ha létezik olyan térbeli tartomány, ahová a tömeg rendelhető. A fekete lyuk esetén megfordul a viszony az Rkötött sugár és a tömeg között, mert már nem a tömeg jelöli ki a határt, hanem annak sugara adja meg a tömeget:

Ebben a felfogásban a fekete lyuk úgy viselkedik, mintha egy gigantikus részecske volna!
A fekete lyuk beszippantja a környezetét, és felhizlalják a befogott fotonok is. Ennek sugara növekszik, de a fénysebességű forgások miatt a részecskékhez hasonlóan a felülete nulla lesz. Ez fejeződik ki a fenti összefüggésben is, amely szerint a tömeg lineárisan és nem harmadik hatványon növekszik a sugárral. Tehát a fénysebességű forgások koncepciója szerint a téridő szingularitása egyfelöl egydimenziós részecskéket, másfelöl egydimenziós fekete lyukakat is megalkothat.
Nézzük meg annak feltételét, hogy az Rkötött sugár az anyagsűrűség növekedésével mikor alkothat fekete lyukat? Ehhez még az is kell, hogy az M tömeget magába záró objektum RM sugara kisebb legyen, mint az a pálya sugár, ahol a foton kering, azaz
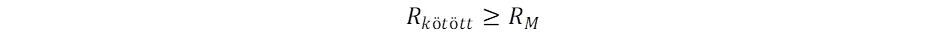
Ha ez nem teljesül, még nem beszélhetünk fekete lyukról, mert ilyenkor az égitest a szokásos módon nyeli el és bocsárja ki a fényt. A fekete lyukhoz szükség van egy olyan külső tartományra, ami körül veszi az objektumot, és azon belül már akkora a térgörbület, ami körpályára kényszerít a fényt. Amíg az objektum tömege nincs teljesen az Rkötött sugarú tartomány belsejében, a tömegvonzás iránya eltérő belül és kívül, és így nem adódik össze. A fekete lyuk kialakulásához a nagy tömeg önmagában nem elég, ehhez extrém nagy tömegsűrűség is kell. Igaz persze, hogy azonos sűrűségű égitesteknél kedvezőbb a nagyobb méret a fekete lyuk kialakulásához, mert a tömeg RM harmadik hatványával növekszik, míg az Rrel relativisztikus sugár egyenesen arányos a tömeggel.
Milyen csillagok lehetnek fekete lyukak?
Nézzük meg a feltételek teljesülését különböző égitesteknél! A Föld esetén a csapdázott foton pályasugara kisebb, mint 5 milliméter, a Napnál pedig 1,5 km körül van, ami jóval kisebb az égitestek kiterjedésénél. A Földre vagy Napba érkező fényt ezért nem a gravitáció fogja foglyul ejteni, hanem az égitestek felületen nyelődik el, és az égitestek felszínéről kibocsátott fénysugarak zavartalanul távozhatnak. A galaktika óriáscsillagjai sem viselkedhetnek fekete lyukként, mert a tömegükhöz tartozó pályasugár nem haladja meg a 200 kilométert, amelynél saját sugaruk sok nagyságrenddel nagyobb. A fekete lyukhoz szükséges nagy sűrűséget sokkal inkább a neutroncsillagoktól várhatjuk. Ezeknek tömege 1 és 3 Naptömeg között változik és sugaruk 10 km körül van. Egy közepes neutroncsillag 3·1030 kg tömegét alapul véve a sűrűség 6·1017 kg/m3-nek adódik, ezzel összevetve a kötött foton pályasugara 2,5 km körül lehet. Ebből látható, hogy a 10 km sugarú neutroncsillagok sem lehetnek fekete lyukak.
Mielőtt tovább lépnénk, érdemes elgondolkozni rajta, hogy mi határozza meg a neutroncsillagok, illetve a fekete lyukak tömegsűrűségét. Induljunk ki a nukleonokból, a protonból és neutronból! A szóráskísérletek szerint a proton sugara rp = 0,87·10-15 m, tömege pedig mp = 1,66·10-27 kg, az ebből számolható sűrűség ρp = 6·1017 kg/m3. A proton tömeg alapján számított Rrel sugár sok-sok nagyságrenddel alatta marad a részecske sugarának, ezért a nukleonok sem lehetnek fekete lyukak. Az égitestek sorában léteznek neutronokból felépült csillagok is, melyek anyagsűrűsége közel van az egyes nukleonokéhoz, vagyis lényegében sűrűn pakolt hatalmas neutron tömbnek felelnek meg. Érdemes azt is megjegyezni, hogy ez a sűrűség meghaladja a nagyobb atommagok sűrűségét, ami 3·1017 kg/m3 körül van. A Standard Modell szerint egyaránt az erős kölcsönhatás tartja egyben a kvarkokat a nukleonokban, és a nukleonokat az atommagokban. Nagyobb atommagoknál két ok is szerepet játszik a sűrűség csökkenésében: egyrészt az erős kölcsönhatás rövid hatótávolsága, másrészt a protonok közötti elektrosztatikus taszítás.
Egy kis kémia
Az atommagok szerkezetének megismeréséhez segít, ha párhuzamot vonunk az atomi elektronpályákkal. Az elektronok héjakba rendeződnek, mert a spinhez két, az L impulzusmomentumhoz 2L +1 azonos energiájú pálya tartozik, és a Pauli elv szerint minden pályán csak egyetlen elektron lehet. Ez vezet a molekulák kialakulásához, mert az egyik atom zárt héja feletti többletelektronját átadhatja egy másik atomnak, ahol a héjból egy elektron hiányzik, ez az ionos kötés. Ennél sokkal fontosabb azonban a kovalens kötés, ahol az atomok „megosztoznak” az elektronokon kölcsönösen kialakítva zárt héjakat. Ennek „nagymestere” a szén, amelynek vegyértékhéja félig van tele, azaz félig üres, és ebből fakad, hogy a szerves vegyületek végtelen sokasága jön létre.
Egy kis magfizika
Az atommagot alkotó protonok és neutronok is héjakba rendeződnek, de itt nagyságrendekkel nagyobb az energia és sokkal kisebb a nukleonok közötti távolság. Erre szükség is van, mert az erős kölcsönhatásnak rövid a hatótávolsága. Az atomok szerkezetének kialakításában három erő: az erős- és gyenge kölcsönhatás, valamint az elektromágneses erő összjátékára van szükség. Az erős kölcsönhatás nem tesz különbséget a nukleonok között, egyforma erővel köt össze két protont, két neutront, vagy egy protont és egy neutront. De akkor miért nem jönnek létre már normál körülményeink között is neutron agglomerátumok, hiszen ekkor nem kellene legyőzni a töltések miatti taszító erőt! Itt lép be a gyenge kölcsönhatás, amely negyedóránként alakítja át a neutront protonná és így a tiszta neutronból felépülő tömbök nem stabilisak. A neutront és protont is tartalmazó atommagokban a gyengekölcsönhatás már nem végzi el az átalakítást, mert a protonok számának növekedése egyrészt erősebb taszítást okoz, másrészt a proton is magasabb energiájú pályára kerülhet. A legstabilabb, azaz a legnagyobb kötési energiával rendelkező atommagokban, ilyen a hélium a neutronok és protonok, egyaránt betöltött pályán helyezkednek el. Ha az atommagban a nukleonok száma n, akkor közöttük n(n-1)/2 pár alakul ki, amivel arányosan növekszik az erős kölcsönhatás hozadéka. Ezért lesz a kötési energia egyre nagyobb az 56Fe izotópig bezárólag. Ha ennél is nagyobb a nukleonok száma, akkor már gyarapszik az olyan „távoli” párok száma, amelyek között nincs erős kölcsönhatás, és ráadásul a nagyobb protonszám növeli az elektrosztatikus taszítást, hiszen ez a kölcsönhatás alig csökken a nukleonok közötti távolsággal. Emiatt válnak bomlékonnyá az olyan atommagok, ahol a protonok száma már közelít százhoz.
A neutroncsillagok fizikája
A neutroncsillagokban már egy új játékos ül le az asztalhoz: a gravitációs kölcsönhatás. Ennek ereje már eléri az erős kölcsönhatás szintjét, de „jobb lapokkal” rendelkezik, mert a kölcsönhatás nincs korlátozva az objektum méretével, ezért képes bármennyi neutron összetartására. De ne felejtkezzünk el a gyenge kölcsönhatásról, amelyik a neutron állományt fokozatosan protonná alakíthatja át, és ha túl sok a proton, az elektrosztatikus taszítás megakadályozhatja a neutroncsillag gyarapodását. Ez magyarázhatja, hogy a tömegük nem haladja meg a Nap háromszorosát.
Szupernóva robbanás
A neutroncsillagok felfedezése 1935-ben James Chadwick (angol csillagász, 1891-1974, Nobel díj: 1935) nevéhez fűződik, aki a szupernóvák robbanását vizsgálta. A robbanás feltételét Subrahmanyan Chandrasekhar (1910-1995, Nobel díj: 1983) indiai csillagász adta meg, mely szerint ehhez akkora csillag kell, melynek tömege legalább nyolcszorosa a Napnak. Amíg a csillagban elegendő a hélium termelő üzemanyag a fúzióhoz, addig a sugárnyomás megóvja a csillagot az összeroppanástól, de amikor ez kezd kifogyni a csillag összeroskad, és hatalmas energia kibocsátás után csak egy viszonylag kis mag marad vissza, ami lehet egy fehér-törpe, vagy egy neutroncsillag. Ez a robbanás nem szállítja el az óriáscsillag eredeti forgásához tartozó perdületet, viszont a tömeg és még inkább a sugár sok nagyságrenddel lecsökken, amiért a forgást akadályozó tehetetlenségi nyomaték sok nagyságrenddel kisebb lesz, felgyorsítva a forgási frekvenciát akár 10 nagyságrenddel is. A neutronok rendelkeznek mágneses momentummal is, mert az alkotó kvarkok töltés súlypontja nem esik egybe. Így a másodpercenként akár több százszor megperdülő csillag mágneses mezője szétküldi az energiát a lágy rádiósugaraktól kezdve a kemény gammasugarakig, létrehozva a pulzárokat.
Mi lehet a fekete lyukak anyaga?
A fekete lyukakról csak keveset tudhatunk, mert egyedül azáltal vehetjük észre jelenlétüket, hogy eltakarják a mögöttük lévő csillagokat. Tömegükre is tehetünk becsléseket a csillagok mozgását tanulmányozva, amit befolyásol a fekete lyuk tömege is. Ezek jellemző tömege a neutroncsillagoknál hozzávetőleg egy nagyságrenddel nagyobb, de a galaxisok centrumában létező óriási fekete lyukak ezt a méretet is sokszorosan meghaladják. A Napnál tízszer nagyobb tömegű objektumokban a kötött fotonok pályasugara már 25 kilométer fölé nő, elérve a fekete lyukak kiterjedését, ha ezek sűrűsége a neutroncsillagokéval egyezik meg. Nem kell tehát a fekete lyukak sűrűségének meghaladni a neutroncsillagét ahhoz, hogy képesek legyenek visszatartani saját sugárzásukat. Kérdés azonban, hogy miért lehet tömegük jóval nagyobb, mint a neutroncsillagoké? Ez úgy képzelhető el, hogy itt nemcsak a neutronok, hanem a protonok, sőt az elektronok is csapdázódnak. A hatalmas gravitációs erő az elektronokat olyan pályára kényszerítheti, ahol a protonok belsejében nagy az elektronsűrűség. Nagytömegű radioaktív atomokban ismert a K-befogás jelensége. Ez azt jelenti, hogy a legbelső pálya elektronját befogja az atommag, és egy proton neutronná alakul át. Ez a folyamat épp fordítottja a bétabomlásnak. A fekete lyukban a protonok belsejében lévő nagy elektronsűrűség miatt a K-befogás valószínűsége is megnövekszik, kompenzálva a bétabomlást, és elősegítve, hogy a fekete lyukak tömege jóval nagyobb lehessen a neutroncsillagoknál.
Hogyan számítsuk ki az anyagsűrűségét nem-euklideszi geometriában?
Az általános relativitáselmélet kilép az euklideszi geometriából, ezért újra kell gondolni a térfogatszámítás szokásos szabályait, amikor az anyag sűrűségéről beszélünk. Könyvünkben a térgörbület jellemzésére a gömb sugarának és felületének arányából indulunk ki, és a gravitációs vonzást a felület csökkenésével értelmezzük. Az euklideszi geometriában a gömb térfogata 4R3π/3, míg a felület 4R2π, a görbületi geometriában ez úgy változik meg, hogy ott a térfogatot a sugár és a felület szorzatának harmadával tesszük egyenlővé. Emiatt a gravitációs vonzásnak megfelelő felületcsökkenés redukálni fogja a térfogatot, a tömegsűrűség pedig ennek arányában növekedni fog. Amikor közeledünk a fekete lyuk szinguláris geometriája felé, fokozatosan nagyobb lesz a tömegsűrűség, ami ezáltal elősegíti a fekete lyuk kialakulását. Fekete lyukakban pedig a téridő szingularitása annak felel meg, hogy ott az anyagsűrűség végtelenül nagy lesz. Ez összhangban van Penrose felfogásával is, aki a fekete lyukak kialakulását a téridő szingularitásával hozta összefüggésbe.
Mekkora lehet a fekete lyuk?
De, a „telhetetlen étvágyú” fekete lyukak méretének mi szab határt? Miért nem falják fel környezetüket, akár az egész galaxist is? Ezt a kérdést vetette fel Stephen Hawking angol elméleti fizikus is (1942-2018). Álláspontja szerint a fekete lyukak is sugároznak, de ennek intenzitása túl gyenge ahhoz, hogy detektálni lehessen. Ez a sugárzás a hőmérsékleti sugárzás analógiája, de szerepet játszhat benne a fekete lyuk forgása is. Ez a kisugárzás visszaveszi a fekete lyuk növekedését, sőt Hawking számításai szerint akár „el is párologhat”. Saját felfogásom szerint a fekete lyuk forgása a sugárzás legvalószínűbb oka, hiszen a fekete lyuk részecsketermészete miatt perdülettel is rendelkezik. Ugyanis a fotonokhoz rendelt belső tömegre hat a forgás centrifugális ereje, amely megbontja a gravitációs vonzás által létesített egyensúlyt, és így a fotonok kiszabadulhatnak a kötött állapotból.
Az s pálya és a gravitációs erő
Az atomok elektronpályáit az L pályakvantumszámmal lehet leírni, ami egész értékeket vehet fel. Az L = 0 un. s pálya különleges tulajdonsággal rendelkezik, mert véges a valószínűségsűrűsége az atommag helyén is (Lásd K3, 88-90 oldal). Az atommag helyén az elektron és a pozitív mag között elvben végtelenül nagy lesz a vonzóerő, hogyan lehet, hogy az elektront mégsem „nyeli el” a mag? A kvantummechanika erre világos választ ad: az energia és erő számításánál a valószínűségsűrűség és az erő szorzatát kell integrálni. A számításban felbontjuk a teret infinitezimális tartományokra, és képezzük a sűrűség és a térfogat szorzatát, vagyis meghatározzuk, hogy az adott tartományban mekkora az elektron tartózkodási valószínűsége. Az atommag helyén a tartomány térfogata 1/R3 arányában csökken, melyet szorozva az 1/R2 szerint növekvő erővel, a szorzatuk nulla felé tart az atommag helyén. Ez azt jelenti, hogy a valószínűségsűrűség ugyan nullától különbözik a mag helyén, azonban a tartózkodási valószínűség mégis nulla lesz.
Miért érdekes ez a gravitációnál? Az atomokban a mag és az elektron közötti elektromos vonzó erő közel negyven nagyságrenddel nagyobb, mint a tömegek közötti gravitációs erő. Tehát a gravitáció olyan gyenge, hogy figyelmen kívül hagyható. De, igaz ez mindenütt? Ez azért kérdés, mert rendkívül kis távolságban már domináns lesz a vonzóerő relativisztikus korrekciója, amely 1/R3 arányában változik, vagyis az atommag helyén már nem lesz nulla a szorzat az erő és az s pálya valószínűségsűrűsége között. Igen ám, viszont ebben a rendkívül szűk tartományban már az atom Schrödinger egyenletében is fellép az 1/R3 szerint növekvő gravitációs potenciális energia, amely olyan megoldáshoz vezet, amelyben már nulla a centrum valószínűségsűrűsége s pályák esetén is.



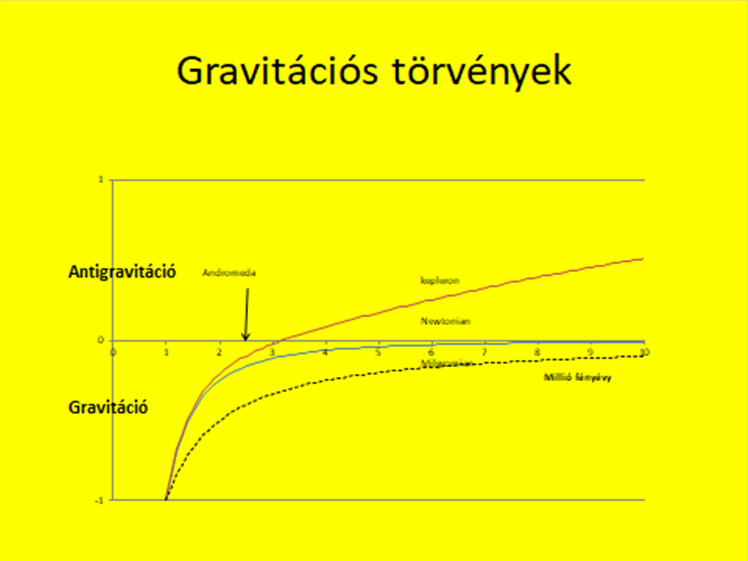




 százmilliárd galaxis taszító kölcsönhatása mind-mind összeadódik szétfeszítve az egész univerzumot.
százmilliárd galaxis taszító kölcsönhatása mind-mind összeadódik szétfeszítve az egész univerzumot.