Bevezetés
Akár a Földre, a Holdra vagy a Napra gondolunk, gömbszerű testet képzelünk el, de ez igaz a Naprendszer valamennyi bolygójára, sőt a távoli csillagokra is. Persze egyik égitest sem tökéletes gömb, pontosabb ellipszoidról beszélni, amely kissé megnyújtott a forgási síkban. A lapultság mértékét egy aránnyal adjuk meg, amely összeveti a két sugár különbségét a sugarak hosszával. Kőzetbolygók esetén, ilyen a Föld is, ez az arány kicsi, például 1:300 Földünk esetén, de már jelentősebb a két gázhalmazállapotú óriásbolygónál 1:16 a Jupiter és 1:10 a Szaturnusz esetén. Nagyon kismértékben lapított a Nap, itt egy a millióhoz az arány. Az arány a bolygók szerkezetét tükrözi, mert a szilárd földkéreg kevésbé enged a forgás centrifugális erejének, összevetve a gázhalmazállapotú bolygókkal.
De miért alakulnak ki a gömbszerű égitestek, kivéve persze a parányi meteoritokat és üstökösöket? Erre a könnyű válasz, ugyan miért is lennének más formájúak, például korongok, vagy lemezformájúak, hiszen a gravitációs erő is gömbszimmetrikus. De csak akkor gömbszimmetrikus a gravitáció, ha eleve gömbalakú testről van szó, amikor a test szimmetriája alacsonyabb, a gravitációs erő is irányfüggést mutat.
Gondolatkísérlet
Mielőtt a címben feltett kérdésre megadnánk a választ, végezzünk el egy gondolatkísérletet. Az R sugarú Föld belsejében hozzunk létre egy üreget, ami teljesen körbeér és a Föld centrumától r távolságban van. Indítsunk el egy rakétát ebben az üregben! Mekkora sebességgel kell elindítani ezt a rakétát, hogy körözni tudjon ebben az üregben? Ehhez azt kell tudni, hogy mekkora lesz a gravitációs erő r távolságban a centrumtól. A tömegsűrűség nem azonos a Föld belsejében, a külső kéregben 2,7 g/cm3, a centrumban felmegy 13 g/cm3 körüli értékre, de most ettől tekintsünk el, és használjunk egy olyan modellt, ahol végig azonos a sűrűség, a Föld esetén ez 5,514 g/cm3.
A Föld felszínén az m tömegre ható gravitációs erő:
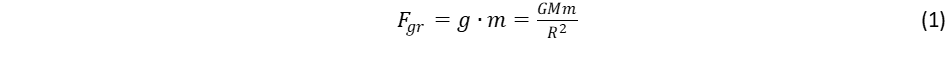
Itt R = 6378km a Föld sugara, M = 5,97·1024 kg a tömege és G = 6,673·10-11 m3/kg·s2 az általános gravitációs állandó. Innen számolva g = 9,81 m/s2 nehézségi gyorsulást kapunk a Föld felszínén. Ezt az összefüggést úgy is megkaphatjuk, hogy az M tömeget a Föld középpontjában helyezzük el. Ez az un. gömbhéj tétel, amit eredetileg Newton állított fel (lásd: en.wikipedia.org/wiki/Shell_theorem). A tételnek van egy második szabálya is, amely szerint egy üres gömbhéj belsejében bárhová elhelyezett testre nem hat gravitációs erő. A tétel levezetésének kulcslépése, hogy integrálásnál a gömb felülete r2-el arányos, ami éppen kiegyenlít a gravitációs erő r2-el arányos csökkenése. Az erő számításban azonban szerepet játszik a sűrűségeloszlás is, amikor a Föld belsejében keressük a gravitációs vonzóerő változását, de gondolatkísérletünkben ettől most eltekintünk. A felettünk lévő rétegek felfelé húznak, az alattunk lévők lefelé, a középpontban épp kiegyenlítik egymást az erőhatások, ezért ott súlytalansági körülmények vannak. Az említett két héj tétel alapján kimutatható, hogy az erő arányosan növekszik a centrumtól való r távolsággal, azaz

Az összefüggés egyaránt reprodukálja az r = R esetén a felszíni gravitációs erőt, és a centrumban a nulla gravitációt.
A gravitáció koherencia törvénye
Keringőmozgás akkor jön létre, ha ez az erő éppen kiegyenlíti a centrifugális erőt:
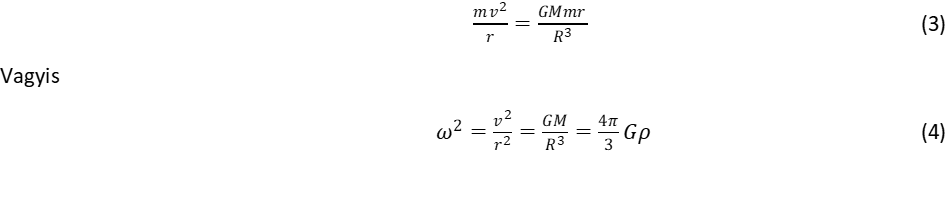
Az összefüggés azt fejezi ki, hogy a keringés ω körfrekvenciája nem változik, ha az r sugár kisebb a Föld R sugaránál, és kizárólag a gömb anyagának ρ sűrűségétől függ!
Bár csupán egy gondolatkísérletből indultunk ki, a nyert eredmény kulcsfontosságú az égitestek kialakulása szempontjából. Eljutottunk ugyanis egy olyan törvényhez, amely magyarázza gömbalakú gázformációk létrejöttét. Ezt a törvényt nevezhetjük a gravitációs mozgás koherencia elvének is. A kozmológia turbulens mozgású és nagysűrűségű molekuláris gázok és porok kondenzációjával magyarázza az égitestek kialakulását. A hidrogén gáz a leggyakoribb kiindulási anyag, de feltételezhető nagyobb rendszámú molekulák részvétele is, mindenekelőtt a kőzet és a „jég” bolygók esetén. Erre Naprendszerünk is példát mutat, ahol kizárólag a két óriásbolygó, a Jupiter és a Szaturnusz épül fel hidrogénből és héliumból, míg a Neptunuszt és Uránuszt jégbolygónak tartják, melyeket közepes molekulatömegű vegyületek alkothatnak, míg a kőzetbolygókban, így a Földben is fellelhetjük a periódusrendszer összes elemét.
A csillagok és bolygók képződésének kozmológiai elmélete
Molekuláris gázok, vagy porok örvényszerű mozgása lehet a csillagok és bolygók képződésének kiindulópontja, melyek centruma indíthatja el a kondenzációt. A nebuláris hipotézis szerint (https://en.wikipedia.org/wiki/Nebular_hypothesis) létrejöhet egy korong szerkezetű „előcsillag” állapot, amely emlékeztet a Szaturnusz gyűrűire egy központi maggal. Az elmélet alapjait még Immanuel Kant rakta le 1755-ben, hogy magyarázza a Naprendszer kialakulását, és elméletét Pierre Laplace fejlesztette tovább 1796-ban. Az elmélet elsősorban a bolygók pályamozgásait kívánja értelmezni, esetünkben azonban a keringési pályák helyett a gömbalakú égitestek kialakulására helyezzük a hangsúlyt. A jelenlegi kozmológia széleskörben elfogadott elmélete Viktor Szafronov munkásságán alapul, akinek erről szóló műve 1969-ben jelent meg. Ezt nevezzük a szoláris nebula-diszk modellnek (Solar Nebular Disc Modell, SNDM).

- ábra. A bolygóképződés SNDM modelljének szakaszai
A gázfázis alaptulajdonságai
Kiindulásként elfogadva ezt a modellt, vessük fel a kérdést, hogyan alakul át a diszk lemezstruktúrája gömbalakba? Először a gázfázis tulajdonságait nézzük meg! Ebben a halmazállapotban a gázmolekulák között nem működik olyan kölcsönhatás, amely egybekapcsolná a komponenseket, hanem szétpattannak ütközéskor. Gravitációs erőtérben, például ahogy a levegő körülveszi a Földet, nem ragadnak hozzá a földkéreghez sem, hanem visszapattannak onnan is, ami lendületváltozást, azaz felületre gyakorolt erőt – vagyis nyomást – idéz elő. Minden egyes molekulát a Föld gravitációs ereje lefele húz, de ennek hatása nem szabadesés, mert az ütközések megtörik a szabad mozgás útját és kialakul egy egyensúlyi állapot. Ebben az állapotban az alsó rétegek tartják maguk felett a magasabb rétegek összegzett súlyát, ezáltal alakul ki a lefelé növekvő nyomás. De létrejöhet-e olyan gázfázisú alakulat, amit nem egy külső gravitációs erő tart egyben? A kérdésre adható válasz vezet el a csillag és bolygó kialakulás folyamatának megértéséhez.
A koherencia és az SNDM modell
Térjünk vissza a gondolatkísérlet kapcsán megfogalmazott koherencia elvhez! Ennek lényege, hogy olyan forgás jön léte, ahol a kerületi sebesség arányos a forgási tengelytől mért távolsággal, vagyis v = ω·r, ahol ω a forgás körfrekvenciája. Ez a szabály egészen természetes, ha szilárd testet, egy kereket vagy gömböt forgatunk meg, mert ekkor a forgatás során a merev test egyben marad, és a forgási tengelytől való távolsággal arányos az egyes pontok sebessége. Itt viszont gázrendszerben létrejövő forgásokról van szó! Az SNDM modell szerint a kaotikusan mozgó molekulák nekiütköznek a központi lemeznek és onnan visszapattannak, de itt lép be a gondolatkísérletből származtatott koherencia szabály: ha épp megfelelő sebességgel és jó fázisban érkeznek bizonyos molekulák, akkor beléphetnek a forgási tengellyel párhuzamos és a központi forgással koherens keringési pályára. Ezáltal viszont megnövekszik a koherens mozgást végző égitest M tömege és R sugara. Ez a nagyobb sugár pedig lehetővé teszi a szélső gyűrű csatolódását a szomszédos külső gyűrűhöz. Ez az alapja a gömbalakú forgó égitest növekedésének. Az egyenletes sűrűséget az biztosítja, hogy a forrásul szolgáló felhő anyaga is homogén. A növekedési folyamat addig tart, amíg a turbulens gáz anyaga biztosítja az utánpótlást.
A nyomás szerepe az égitestek szerkezetében
A gömb növekedése együtt jár a centrumban kialakuló nyomás növekedésével. A nyomás ugyanis –ellentétben az erővel – fokozatosan növekszik a centrum felé haladva, mert ekkor az egyes rétegek súlya összeadódik, hasonlóan ahhoz, ahogy a vízben is annál nagyobb a nyomás, minél mélyebben vagyunk. A centrumban a nyomást a
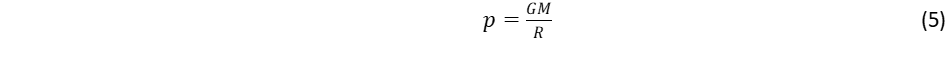
összefüggés adja meg. A Föld esetén ez az érték 350 GPa körül van.
Ha gázról van szó, akkor a nyomás hatására növekszik a hőmérséklet és a sűrűség a p·V = R·T törvény szerint, ahol V a térfogat, T az abszolút hőmérséklet Kelvin fokban és R =8,314 J·mol-1·K-1 az általános gázállandó. (Itt R nem tévesztendő össze a gömb R sugarával!). A koherencia szabály nem engedi meg, hogy a centrum felé haladva a növekvő nyomás térfogatcsökkenést és ezáltal sűrűség növekedést okozzon, mert ez megszüntetné a forgási koherenciát. (Figyelem: a koherencia előfeltétele a homogén sűrűség!). Mivel a V érték állandó, így az égitest M/R-el arányos nyomásnövekedése a hőmérséklet emelkedését idézi elő. A Jupiter esetén 28-szor, a Napnál pedig már 286-szor nagyobb nyomással kell számolni a Földhöz képest. A rendkívül nagy nyomás és magas hőmérséklet a Nap belsejében megindítja a termonukleáris reakciót, melynek során a hidrogén atommagok fúziója héliumot eredményez, szemben a Jupiterrel és Szaturnusszal, ahol ez a folyamat nem jön létre.
A forgási frekvenciák kapcsolata a bolygók sűrűségével
A (4) egyenlet kapcsolatba hozza az ω koherencia frekvenciát az égitest sűrűségével. De milyen a kapcsolat az egyes bolygók forgási frekvenciája és a koherencia frekvencia között? Ezt összegezzük a Táblázatban, de kihagyva a két belső bolygót, ahol az árapály jelenség miatt a bolygó forgási sebessége nagymértékben lelassult.
|
Bolygó |
Fordulat ideje/óra |
Koherencia idő/óra |
Lassulási arány |
Sűrűség g/cm3 |
Lapultság |
Tilt szög |
|
Föld |
23,95 |
1,405 |
17,05 |
5,514 |
1/300 |
23,44 |
|
Mars |
24,6 |
1,664 |
14,78 |
3,934 |
1/700 |
25,19 |
|
Jupiter |
9,92 |
4,168 |
2,38 |
1,326 |
1/15,4 |
3,13 |
|
Szaturnusz |
10,55 |
3,981 |
2,65 |
0,687 |
1/10,2 |
26,73 |
|
Uránusz |
16,0 |
2,579 |
6,20 |
1,637 |
1/43,6 |
82,23 |
|
Neptunusz |
17,23 |
2,927 |
5,89 |
1,271 |
1/58,5 |
28,32 |
- Táblázat. A naprendszer hat bolygójának forgási, sűrűségi és lapultsági adatai
A koherencia frekvenciához képesti lassulás érthető, hiszen az égitest felépülése után az egyben maradást elősegítik a gravitációs hatást kiegészítő molekuláris kölcsönhatások, ami együtt jár az anyag lokális sűrűségének változásával, illetve növekedésével. A bolygó adatok arra utalnak, hogy lineáris korreláció van a forgási lassulás mértéke és az átlagos sűrűség között.

- ábra. A bolygók forgási lassulása és sűrűsége közötti kapcsolat (S: Szaturnusz, J: Jupiter, N: Neptunusz, U: Uránusz, M: Mars, F: Föld)
A két gázbolygó esetén a legkisebb a lassulás, ennek duplája a jégbolygóké, de ennél is jóval nagyobb a kőzetbolygóké. Ez világosan tükrözi a halmazállapotok eltérését. A bolygók sűrűsége még a gázbolygóknál is közel van a vízéhez, vagyis kondenzáltnak tekinthető, ahol a gázmolekulák távolsága olyan kicsi, ahol már szerepet játszanak a molekulák közötti vonzó erők (Van der Waals, illetve dipólus kölcsönhatás). A jégbolygók nagyobb sűrűsége erősebb kölcsönhatásra utal a molekulák között, kőzetbolygókban pedig még tovább növekszik a részecskéket összetapasztó erő, ahol már erős kémiai kötések alakulnak ki az atomok közötti. A fenti ábra tanulsága, hogy a bolygó alkotóelemeit összekötő energia lassítja a bolygók forgási sebességét. Szintén a bolygók anyagát egybetartó erőkre utalnak a lapultsági adatok, a gázbolygók lapultsága jelentős mértékű, 1/10 körül van, a jégbolygóké 1/50, viszont a kőzetbolygók nagyon enyhén lapultak, nagyságuk 1/500 körül van.
Bolygó perdületek
A bolygók forgási sebességének lassulását vizsgálhatjuk az energiamérleg és a perdület szempontjából is. A kötött pályán keringő bolygók a forgás miatt más-más régiójukat mutatják a velük gravitációs csatolásban álló Nap felé. Föld esetén ennek látványos megnyilvánulása a tengervíz emelkedése és süllyedése, az ár-apály jelenség, bár ebben a Hold fontosabb szerepet játszik, mint a Nap. A víz mozgása során a mechanikai energia részben hőenergiává alakul át az entrópia törvénynek megfelelően. Végső soron ez a forgási energia csökkenését okozza, ami a bolygók forgási sebességének lassulásában mutatkozik meg. Az ár-apály jelenség lassító hatása különösen nagy a Hold esetén, ahol már teljesen leállt a forgás, és emiatt a Hold mindig ugyanazt az oldalát mutatja felénk. A bolygók közül a Merkur forgása állt le hasonlóképpen. A forgás lassulása hosszú folyamat, ami jóval intenzívebb volt, amíg nem szilárdult meg a bolygók külső kérge. Ez tükröződik abban, hogy a Földön jelenleg 24 óra hosszúságú a nap, szemben a koherencia elvnek megfelelő másfélórával.
A forgás lassulásának van egy perdületi oldala is: hová tűnik el a perdület (az impulzusnyomaték), amikor lelassul a forgás? A bolygók perdületét egyrészt a keringés, másrészt a forgás adja ki, jelöljük a két összetevőt L és S vektorokkal. Ekkor a teljes J perdületet a vektorok összegzési szabálya adja meg (a vektorokat félkövér betűk, a skaláris abszolútértéket dőlt betük jelölik):
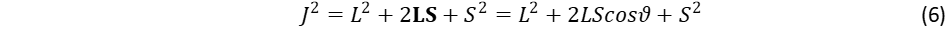
Itt ϑ az L és S vektorok közötti szög, az un. „tilt” szög a bolygó forgási tengelye és a keringési pálya normálisa között, ez megfelel az inklinációs szög pótszögének. A perdület két komponense több nagyságrenddel különbözik, például a Föld esetén a keringési járulék 4,5 milliószor nagyobb, mint ami a forgásból származik. A nagy különbség oka, hogy a keringési sugár több nagyságrenddel haladja meg a bolygó sugarát, a Föld esetén az arány 150 millió a 6378 kilométerhez, és a tehetetlenségi nyomaték az arány négyzetével arányos. A tilt szögnek az a jelentősége, hogy ez határozza meg a forgási-keringési csatolás hatékonyságát, amikor közvetíti a forgási perdületet a keringési perdület felé. Minthogy az utóbbi jóval nagyobb, így a forgás lassulása csak nagyon kevéssel növeli meg a keringési frekvenciát.
A Nap esetén is összehasonlíthatjuk a koherencia frekvenciát a nap forgási sebességével, itt a lassulás mértéke sokkal-sokkal nagyobb, mint amit a bolygóknál láttunk, mert a termonukleáris reakciók beindulása új helyzetet teremt. Itt a gravitációs nyomás olyan nagy, hogy már nem az atomok, hanem az atommagok kapcsolódnak össze a nukleáris erők által. Ennek hatása mutatkozik meg abban, hogy a bolygókhoz képest a forgási sebesség lelassul és a centrifugális erő csak kismértékű lapultságot idéz elő. A forgási perdület elvesztését a Nap esetén is az orbitális perdülettel való csatolás közvetíti, melynek forrása a Nap keringő mozgása a Tejút központja körül.
A bolygórendszer kialakulásának körülményei
Hogyan alakult ki a naprendszer, hogyan csatlakoztak az egyes bolygók a Naphoz? Nem mehetünk vissza 4 és fél milliárd évvel a múltba, hogy ezt ellenőrizzük, ezért csak néhány spekulatív feltételezést tehetünk. A Nap körüli nyolc bolygó tulajdonságai annyire különböznek, hogy nem valószínű a bolygók egyidejű csatlakozása, sokkal valószínűbb, hogy a Nap Tejútban való kalandozása során különböző helyeken szedte össze bolygóit. Egyedül a Jupiter esetén látszik valószínűnek, hogy ugyanabból a molekuláris felhőből származik, mint a Nap, hiszen közel azonos a sűrűségük (a Napé 1,408 g/cm3), ami valószínűsíti a közös eredetet, ráadásul a Jupiter tilt szöge közel nulla (vagyis a molekuláris felhő turbulencia síkjához igazodhatott a Jupiter pályasíkja és forgási tengelye). Ugyanakkor a Szaturnusz sűrűsége csak feleakkora és elég jelentős a tilt szög. Elképzelhető, hogy a Szaturnusz az eredeti felhő maradékából építkezett, amelynek már kisebb volt a sűrűsége. Lehet, hogy a Szaturnuszt övező gyűrű struktúra az elő-bolygó maradéka? Ez ellen szól azonban, hogy újabb megfigyelések szerint a gyűrűk jóval fiatalabbak, mint az égitest maga. Gyökeresen más lehet a három kőzetbolygó és a törpe bolygók sokaságának eredete, melyek jelentős mennyiségben magas rendszámú elemet is tartalmaznak. Alighanem olyan környékre is eljuthatott a Nap, ahol egy szupernova robbanás törmelékeivel futott össze. Külön története lehet az Uránusznak és Neptunusznak is, erre utal, hogy az Uránusz közel 90 fokos tilt szöge nagyon gyenge keringési-rotációs csatolást jelez. Ezek a jelenségek már túlmutatnak az írásunkban felvetett kérdésen.
Összefoglalás
A Newton által megfogalmazott gömbhéj tételből kimutatható, hogy a homogén sűrűségű gömbökben a gravitációs forgások koherenciában vannak. A koherencia szabállyal kiegészítve a bolygók és csillagok képződési elméletét, magyarázatot kapunk arra a kérdésre, hogy miért gömbalakzatúak a bolygók és csillagok. A naprendszer egyes bolygóinak tulajdonságait a forgási és perdületi viszonyok alapján elemeztük.


