Hogyan vezet el a relativisztikus energiaegyenlet a Higgs bozon koncepcióhoz
Pozitív-negatív, jó-rossz, hideg-meleg, múlt-jövő, jobbra-balra és még sokáig sorolhatnánk az ellentétpárokat: gondolkozásunk egyik alapköve az alternatívák, ellentétpárok szembe állítása. A fizikai fogalmak világában is kulcsszerepet játszanak a kétértékű mennyiségek, amelyeket valamilyen szimmetria köt össze, és amelyek tulajdonságait matematikai összefüggések által adjuk meg. Ezek tovább lendítik megértésünket a fizikai valóságról, de gyakran csapdába esünk, ha már jobban hiszünk egyenleteinknek, mint annak a valóságnak, mint amiből egyenleteink származnak. Ezt a felfogást nevezném matematikai fetisizmusnak. Először egy ilyen példából indulunk ki, majd nekifogunk, hogy bemutassuk az elemi részecskék világának legfontosabb alternatíváit, és kísérletet teszünk arra, hogy a Higgs bozont is beillesszük a fénysebességű forgások közé.
Honnan ered a lyukelmélet?
A matematikai fetisizmus egyik legismertebb példája a lyukelmélet. Ennek megértéséhez a relativitáselméletből kell kiindulni, amelyik már önmagában is sok félre- és belemagyarázás kiindulópontja. A klasszikus mechanika alapjait Newton fektette le, kimondta az erő és a gyorsulás arányosságát, amit a tehetetlen tömeg kapcsol össze, és megfogalmazta az energia megmaradás tételét, amely a mozgási és potenciális energia összegének állandóságát mondja ki. A törvények matematikai alakja jól írja le a kis sebességek világát, de már korrekcióra szorul nagy sebességek esetén, amikor beleütközünk egy felső korlátba, amit az átléphetetlen fénysebesség szab meg. A mechanika relativisztikus szabályait az elektrodinamika Maxwell egyenletei alapozzák meg, amely elvezetett a mozgási energia fogalmának továbbfejlesztésére is. A klasszikus mechanika az EKin = ½mv2 összefüggésből definiálja a kinetikus energiát, ezt váltja fel a kovariancia törvény
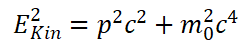
Ez a törvény kis sebességeknél, azaz amikor a p·c impulzus tag kicsi az m0c2 nyugalmi energiához képest, reprodukálja a szokásos kinetikus energiát, ha alkalmazzuk a négyzetgyökvonás sorfejtési szabályát. Az eltérés csak abban jelentkezik, hogy a teljes kinetikus energia tartalmazza a nyugalmi energiát is:
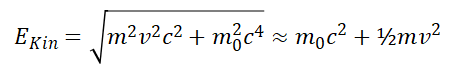
Honnan származik a kovariancia törvény szokatlan négyzetes összeadási szabálya? Ilyen szabály vektorok összeadásánál természetes, de hát miért lenne vektoriális eredetű a nyugalmi energia? Talán mégis valamilyen mozgás bújik meg mögötte? Az összefüggés négyzetes jellege érthető, ha a nyugalmi energia valójában a részecske saját belső forgásának kinetikus energiája, és a külső és belső mozgások impulzusát a vektorok összegzési szabálya szerint adjuk össze, és figyelembe vesszük, hogy a saját forgás gömbszimmetriája miatt nem képződik kereszt tag a kétféle mozgás között.
Problémát jelent, hogy a négyzetgyökvonás két előjelet adó művelet, amiért negatív kinetikus energia és negatív nyugalmi tömeg is származtatható a kovariancia szabályból. De mit lehet kezdeni a negatív értékekkel? A negatív tömeg például azt jelentené, hogy a test a ráható erő irányával ellentétes irányban mozog. Ilyesmit a természetben nem lehetett megfigyelni. Az igazi problémát a relativisztikus kvantummechanika hozta elő, amikor a kovariancia törvénybe bevezették a fizikai mennyiségek operátorait. Mivel a potenciális energia és a kinetikus energia skalárként (lineárisan) és nem vektorként (négyzetesen) adódik össze, így nem kerülhető el a négyzetgyök kibontása, amit Dirac négydimenziós spinorok bevezetésével oldott meg. Az eljárás négykomponensű lineáris differenciál egyenletrendszerre vezetett. A négyzetgyökvonás szabályai miatt a számítások nem csak pozitív, hanem negatív energiájú megoldásokat is adtak. Ekkor következett be az a pont, amit a matematikai fetisizmusnak nevezhetünk: megpróbáltak a negatív energiájú megoldásnak is fizikai értelmet adni. A kvantummechanikában ugyan mindig az energiakülönbségnek van értelme, mert ez határozza meg a kibocsátott, vagy elnyelt fotonok energiáját, így elvben az energia nullapontja tetszőleges lehet. Viszont ennek a negatív energiának nincs alsó határa, ami avval jár együtt, hogy ez elektronnak el kellene tűnnie. Ezt próbálta magyarázni Dirac avval a hipotézissel, mely szerint a tér mindenütt már fel van töltve végtelen számú negatív energiájú elektronnal, és így a valódi elektronok már efölött a „tenger” fölött lebegnek. Az abszurdnak tűnő elmélet megerősítést nyert a pozitron felfedezésével, amelynek tulajdonságai egyeztek az elektronnal, csak a töltése volt pozitív, és elektronnal ütközve a két részecske megsemmisíti egymást gamma-sugarak kibocsátásával. Ez jól beleillett a képbe, mert ha a negatív elektronok tengeréből hiányzik egy részecske, annak tulajdonságai pont megfelelnek a pozitronénak.
Ettől kezdve vált gyakorlattá az elméleti fizikában, hogy a valóságot igyekeztek hozzáigazítani a matematikai egyenletek kívánalmaihoz. Ez az, amit matematikai fetisizmusnak nevezhetünk. A helyes út viszont, hogy ki kell jelölni a matematikai formulák érvényességi határát! Végül is minden egyenlet egy „hasonlat”, amely elősegíti a jelenségek megértését, de a hasonlat nem maga a valóság. Ha az egyenlet – például a kovariancia törvény – különböző megoldásokat, esetünkben negatív energiát is felkínál, akkor azt kell megnézni, hogy találunk-e olyan fizikai jelenséget, amely indokolja, hogy helyesnek fogadjuk el-a negatív értéket. Ha viszont ilyen indokot nem találunk, akkor mondjuk ki, hogy a szóban forgó megoldás hamis.
Az idő irányának megfordíthatatlansága
Nézzük hát a negatív energia kérdését! A probléma gyökerét ott kell keresni, hogy a kvantummechanika egyenletei nem ismerik az idő irányát. A fizikában az entrópia növekedés elve az egyetlen, amely megtiltja a múltba való visszalépést. Ennek lényege, hogy az energiaátalakítási folyamatok mindig veszteséggel járnak, a korábbi állapotba való visszatérés nem lehetséges a képződő hőenergia miatt, ami annak felel meg, hogy az energiakonverzió a magasabban rendezett állapotból kevésbé rendezett állapotot hoz létre. A kovariancia elv sem különbözteti meg az idő irányát, ez bújik meg a negatív energia jelentkezésében is. Az energia és az idő a kvantummechanikai felfogás szerint egymás „ikertestvére”: az energia operátora az idő függvényében képzett differenciálhányadossal arányos, és emiatt az idő irányának megfordítása magával hozza az energia előjelének megfordulását. Az idő irányának megfordíthatatlansága miatt a Dirac egyenlet matematikai megoldásából kapott negatív energiájú állapotok tehát a valóságban nem léteznek, ezeket a fizikai valóság szempontjából hamis megoldásának kell tekinteni, és nem kell attól tartani, hogy az elektron „leesik” a negatív végtelen energia állapotába.
A királis szimmetria szerepe a részecskefizikában
A fénysebességű forgások koncepciója az elektron-pozitron kettősségre egyszerű magyarázatot ad: mindkét részecskét kéttengelyű forgások alkotják, melyek királis szimmetriája fordított, az egyiknek jobbkéz, a másiknak balkéz szimmetria felel meg a két forgás eltérő sodrásiránya miatt.
Ehhez kapcsolódik egyrészt a töltések ellenkező előjele, másrészt a két részecske egymást megsemmisítő reakciója is: a kettős forgások egyike az ellentétes forgásirány miatt megsemmisül, a másik viszont megmarad, hiszen azonos a forgásirányuk, ez a megmaradó egytengelyű forgás pedig a képződő gammasugárzás fotonja.
Lehet-e negatív a tömeg?
A kovariancia elv négyzetes felépítéséből további következtetések is levonhatók. Nézzük először a tömeg kérdését! Mind a nyugalmi energia, mind az impulzus a négyzeten szerepel. Ez alapján a tömeg is lehetne negatív! Ez látszólag ellentmond korábbi állításunknak az E = mc2 ekvivalencia szabály miatt. Viszont a kovariancia elvvel adekvát összefüggés
E2 = m2c4
formában adható meg. Ha így fogalmazzuk meg a tömeg és energia ekvivalenciáját, akkor már szabad az út a negatív tömeg felé! Milyen fizikai folyamat indokolja, hogy beszéljünk negatív tömegről? Hát az anyag és antianyag kettőssége! Ezt úgy fogalmazzuk meg, ha a pozitív tömegű elektron találkozik a negatív tömegű pozitronnal, akkor a két tömeg megsemmisülése idézi elő az annihilációt! Ez eddig csak az annihilációs folyamat újfajta értelmezése, de a negatív tömegnek van ennél sokkal fontosabb megjelenése is, mert képes magyarázatot adni a neutrínó rejtélyre és kulcsot ad a kvarkok különös tulajdonságainak megértéséhez is.. A neutrínó rejtély abból fakad, hogy a mérési pontosság határain belül a neutrínó mindig fénysebességgel halad, ami csak nulla nyugalmi tömegű objektum – ilyen a foton – esetén lehetséges. Viszont a neutrínó oszcilláció jelensége szerint létezni kell három különböző neutrínónak. Mivel a neutrínónak nincs töltése és a spinje ½, akkor mi lehet közöttük a különbség, ha még a tömeg is egyezik (azaz nulla)? A választ a kvantummechanika szuperpozíciós elve és a negatív tömeg fogalmának bevezetése adja meg. A szuperpozíció elve azt jelenti, ha két állapotot valamilyen szimmetria köt össze és azonos energia tartozik hozzájuk, akkor a két állapot szuperpozíciója is érvényes állapotfüggvény. Fogjuk úgy fel a neutrínót, mint olyan szimmetrikus állapotok szuperpozícióját, amelyben az egyikhez pozitív, a másikhoz negatív tömeg tartozik, és a szuperpozíciós súlyfaktor azonos. Az ilyen állapotban már nulla lesz a tömeg, és emiatt nincs akadálya, hogy a neutrínó fénysebességgel haladjon. Ugyanakkor az egymást kiegyenlítő +m és –m tömegek más-más értéket vesznek fel a neutrínók három típusában.
Az anyag jellegű részecske (például elektron) antianyag párja (pozitron) abban is különbözik, hogy fordított elektromos töltésük előjele. Például az elektron töltése –e, a pozitroné pedig +e. A neutrínót alkotó szuperpozíciós állapotban az egyenlő súlyfaktorok miatt a két töltés kompenzálja egymást, és ezért a részecske elektromosan semleges lesz.
A spin megjelenése a relativisztikus kvantummechanikában
Vizsgáljuk meg a kérdést, hogyan került be a spin fogalma a Dirac formalizmusba? Ez is a kovariancia elv négyzetes jellegére vezethető vissza. A Dirac egyenlet az elektron elektromágneses kölcsönhatásait írja le. A potenciális energiának két tagja van, az egyik a Փ(r) skaláris potenciál, a másik az A(r) vektorpotenciál. (Itt és a továbbiakban a vastagon szedett szimbólumok jelölik a vektorokat). Az előbbiből származik az elektromos mező a grad, az utóbbiból a mágneses mező a rot vektor algebrai műveletei által. A potenciálokat az elektromos töltéssel szorozva kapjuk meg az elektromágneses energiát. Mivel az elektromos mező a statikus töltésekből, a mágneses mező a mozgó töltésektől (áram) származik, így a relativisztikus energiához való hozzájárulások eltérő: az elektromos mező potenciális energiája lineárisan adódik hozzá a kinetikus energiához, viszont a mágneses energia közvetlenül az impulzust egészíti ki, hiszen mindkét mennyiség a sebességgel arányos. A Dirac elektron energiája elektromágneses térben:
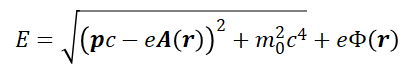
A négyzetgyök felbontása spinorokkal
A fenti kifejezésben a töltést és a tömeget még konstansok képviselik. A négyzetgyökvonást a mátrixtechnikával bonthatjuk fel négydimenziós spinorok bevezetésével. Nézzük meg a spinor felbontás alapelvét, amikor egy háromdimenziós a vektor és egy skaláris b mennyiség négyzetösszegét úgy visszük ki a négyzetgyök alól, hogy abban a vektoriális a és a skaláris b tagok lineáris összege szerepeljen, és az együtthatókat a négydimenziós spinor elemei adják meg:
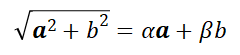
A felbontás megköveteli, hogy a vektoriális α és a skaláris β spinor mátrixok négyzete egységmátrixot alkosson, a komponensek szorzata pedig legyen antiszimmetrikus. A szóban forgó spinorok felépítése visszavezethető 2x2 dimenziós Pauli mátrixokból képzett blokkokra:
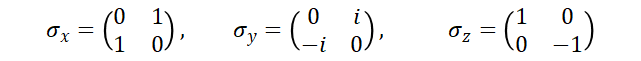
Ezekre a Pauli mátrixokra is teljesül, hogy négyzetük az egységmátrix és szorzatuk antiszimmetrikus (azaz xy + yx = 0). Az elektronspin vektorát a Pauli mátrixokkal lehet definiálni: S = ½σ. A Dirac által alkalmazott spinoros felbontás egyetlen tagként kezeli az impulzusból és a mágneses mezőtől származó tagot. Az utóbbiban a vektoralgebrai művelet elvégzése adja ki a Zeeman energiát:
EZeeman = μBσ·B = 2μBS·B
ahol μB = eħ/2mc a Bohr magneton és B a mágneses mező vektora. A szokásos konvenció szerint a B mező irányában vesszük fel a z tengelyt, ezért
EZeeman = μBσzB = 2μBSzB
Itt B jelöli a B vektor abszolút értékét. Mondanivalónk szempontjából annak van jelentősége, hogy a kovariancia elvből következik az a kétértékűség, ami a mágneses mezőben felvett energia pozitív vagy negatív előjelében mutatkozik meg. Szemléletesen ez a kettősség annak felel meg, hogy az elektron a mágneses mező körül két sodrásirányban végezhet forgásokat: jobbra és balra, és az egyik energianövekedéssel, a másik csökkenéssel jár együtt.
A töltés- és tömegoperátorok bevezetése
Terjesszük ki a kvantummechanika szokásos formalizmusát, amely csak az energiát, impulzust és impulzusnyomatékot írja le operátorokkal, míg a kifejezésekben a tömeg és a töltés konstansként szerepel. Vezessünk be kétdimenziós operatorokat a tömeg és a töltés számára is, amelyeknek két lehetséges sajátértéke van: az egyik pozitív a másik negatív. Ez a töltésoperátor esetén –e és +e, a tömegoperátornál +m és –m. Ez a leírás analóg a spinre (impulzusnyomatékra) érvényes szabállyal, ahol az Sz spinkomponens +½ és -½ értékeket vehet fel.
Lépjünk túl azon a gyakorlaton, amely az impulzushoz kötődő kinetikus energiát és a mágneses kölcsönhatás energiáját egyetlen tagként kezeli a négyzetgyökös kifejezésben. Ez a töltés operátor bevezetésével oldható meg, ami által tetszőleges elemi fermion (elektron, pozitron, neutrínók, kvarkok) leírására alkalmas formalizmushoz jutunk. Annak mintájára, ahogy a fermionok impulzusnyomatékát a spin z komponensével jellemezzük, azaz Szħ = ½σzħ, vezessük be a töltés és tömeg operátorát a z irányú Pauli mátrix segítségével:

A mátrixok vesszőzése azt fejezi ki, hogy ezek a Pauli mátrixok a kétdimenziós királis térben működnek, és nem a spin forgások terében. Ennek a kétdimenziós mátrixnak bevezetése avval jár együtt, hogy a spinor felbontásban nyolcdimenziós mátrixok lépnek fel, melyekre szintén érvényes, hogy négyzetük az egységmátrix és szorzatuk antiszimmetrikus.
A relativisztikus kovariancia elv a fizika olyan általános törvénye, amely valamennyi részecskére vonatkozik. Az összefüggés négyzetgyökének 8 dimenziós spinorokkal való felbontása vezet el az elemi részecskék tulajdonságainak meghatározásához. A fénysebességű forgások koncepciója specifikus kettősforgásként értelmezi a fermionokat. Az egyes részecskék sajátságait az határozza meg, hogy mekkora a királis arány. Az elektron és pozitron tiszta királis állapotnak felel meg, szemben a neutrínókkal és kvarkokkal, ahol keveredik a két királis szimmetria, és ezt a keveredést neutrínóknál a gyenge kölcsönhatás, kvarkoknál az erős kölcsönhatás idézi elő. Evvel kiterjesztjük a nukleáris erők szerepét, melyeket olyan mezőnek tekintünk, amely „kiválasztja” a részecskék forgásának szimmetriáját. Értelmezzük a Zeeman kölcsönhatás mintájára a királis térben működő erőket és a hozzá tartozó energiát:
Egyenge = σ’·Fgyenge és Eerős = σ’·Ferős
A királis állapotok keveredésének mértékét – azaz a részecske töltését – az határozza meg, hogy az F erő iránya mekkora χn szöget alkot a z tengellyel:
En = [σ’xsin(χn) + σ’zcos(χn)]Fn
Itt Fn az erő abszolút értéke, míg a különböző fermionokat létrehozó erő irányszöge:
cos2(χn) =(n+3)/6
Az n kvantumszám határozza meg a részecskék alapvető paramétereit. Az n = 0 kvantumszám esetén a két királis szimmetria egyenlő arányban keveredik, az n = 1 és n = 2 eset felel meg a down illetve up típusú kvarkoknak, míg ha n = 3, akkor kapjuk a tiszta királis állapotot, ez felel meg az elektronnak és a pozitronnak.
Az n kvantumszám által meghatározott töltésmátrix diagonális elemei adják meg az elemi fermionok töltését. A spinek analógiájára bevezetett kétértékűség a töltésen kívül a tömegre is vonatkozik. Neutrínó állapotban a töltés és a tömeg egyaránt nulla, mert a két operátornak nullák a diagonális elemei. Ez teszi lehetővé, hogy a neutrínók fénysebességgel haladjanak. A két kvark típus esetén a töltés és tömegoperátornak egyaránt vannak diagonális és nem diagonális elemei. A diagonális elemek adják ki a ±2/3e és ±1/3e töltéseket. Mivel a tömeg operátor sem diagonális, így a kvarkokhoz nem tudunk valódi tömeget rendelni és a Standard Modell csak renormált tömegekről beszél. A kvark állapotok létrejöttéhez szükség van az erős kölcsönhatás jelenlétére, ennek rövid hatótávolsága miatt ez az állapot csak a kvarkokból felépülő hadronok (barionok és mezonok) belsejében van jelen. Ez magyarázza, hogy szabad kvark – azaz tört töltés – nem figyelhető meg. Ugyanúgy evvel lehet magyarázni, hogy csak egész töltésű hadronok, azaz tiszta királis állapotok jöhetnek létre a két, illetve három kvarkból felépülő hadronokban.
Higgs bozon a fénysebességű forgásmodellben
Felmerül a kérdés, hogy a Higgs bozon hogyan illeszthető be az eddig vázolt keretek közé? Ez az egyetlen olyan elemi részecske, amelynek az elmélet szerint nulla a spinje. Ilyen részecske állapot úgy jöhet létre, ha a Higgs mezőnek is van állapot kiválasztó szerepe. Ez a mező azonban nem a királis térben, hanem a spin forgási terében fejheti ki hatását, mégpedig merőlegesen a z irányra:
EHiggs = σx·FHiggs
Úgy is mondhatjuk, hogy a vessző nélküli Pauli mátrix x komponensével arányos mező váltja ki azt a szimmetriatörést, amely létrehozza a tömeggel rendelkező, de nulla spinű Higgs bozont. Ekkor az Sz = ½ és Sz = -½ állapotok szuperpozíciós súlya megegyezik, és nulla lesz a részecske spinjének várható értéke, tömege viszont mégis lehet. Tehát a Higgs bozon olyan állapotot reprezentál, amelyben a spin két sodrásiránya „egybe van csomagolva” a szuperpozíciós elv révén.
Végkövetkeztetésként megállapíthatjuk, hogy a relativisztikus kovariancia elvből a részecskék három alapvető kettősségére következtethetünk: a spinre, a tömegre és a töltésre. Ez alapján is osztályozhatjuk a Standard Modell részecskevilágát. Az elektron típusú fermionok mindhárom alaptulajdonsággal rendelkeznek, a neutrínónak viszont csak spinje van. A kvarkok is rendelkeznek spinnel, de mérésekkel detektálható töltésük és tömegük nincsen. A bozonok közül a fotonok csak spinnel rendelkeznek, a gyönge kölcsönhatás bozonjainak van spinje, tömege és lehet töltése is. A gluonoknak szintén van spinje, lehet töltésük is, de tömegükről nem beszélhetünk. Végül ott van a Higgs bozon, melynek csak tömege van, spinje nulla és várhatóan nulla a töltése is. A Higgs bozon tulajdonságainak ismerete jelenleg még nem tekinthető teljesnek.
A blog további írásai elérhetők: "Paradigmaváltás a fizikában"