Mi a fény?

Rockenbauer Antal

Maxwell történelmi jelentőségű felismerése volt, hogy az elektrodinamikai alapegyenletek a fényhullámokat is leírják, amivel az optika és az elektrodinamika szintézise létrejött. Ennek fontosságát így emeli ki Feynman [1]

„A fizika fejlődésének legdrámaibb fordulatai azok, amikor a nagy szintézisek végbemennek, amikor különbözőknek látszó jelenségekről hirtelen kiderül, hogy voltaképpen egyazon folyamat különböző megnyilvánulásai. A fizikai tudomány sikerének alapja az, hogy képesek vagyunk ilyen szintézisekre.

A fizika XIX. Századi fejlődésének talán legdöntőbb pillanata az volt, amikorm1860-ban egy szép napon J. C. Maxwell az elektromosság és a mágnesség törvényeit összekapcsolta a fény viselkedésének törvényeivel. Ennek eredményeképpen sikerült részben megmagyarázni a fény tulajdonságait . . . a fényét, amely ősidők óta finom, rejtélyes szubsztancia volt, olyan fontos, hogy a világ teremtéséről szóló fejezetben a bibliaírók külön aktusként írták meg a fény teremtését. „

Az igazsághoz az is hozzátartozik, hogy Maxwell sem előzmények nélkül alkotta meg a klasszikus elektrodinamika máig érvényes elméletét. Munkásságát a kísérletek és az elméleti felismerések hosszú útja előzte meg, melyek sorából érdemes kiemelni Gauss, Ampère és Faraday eredményeit.

A fentieken kívül emeljük még ki, hogy a Maxwell-egyenletek már magukban hordozták a speciális relativitás elvét is, hiszen Lorentz ebből vezette le alapvető transzformációs egyenleteit. Ezen túlmenően a hullámegyenletek megfogalmazása előkészítette a XX. századi fizika másik forradalmi felismerését, ami elvezetett a hullámmechanika, vagy más néven a kvantummechanika megalkotásához.

 Mi az a fizikai közeg, amiben az elektromágneses mező oszcillál? 

Felvetődik a kérdés, hogy mi a hullám közege, végül is mi az, ami mozog? A hang esetén a levegő gázmolekulái, a tenger hullámait a víz hozza létre, a húrnak saját anyaga rezeg, ha megpendítjük, de mi oszcillál a fény esetén? Maxwell még valamilyen viszkózus közegre gondolt, később bevezették az éter fogalmát, de a relativitáselmélet alapján ma már világos, hogy ilyen közeg nem létezik. A téridő-részecske koncepció alapján válaszolhatunk erre a kérdésre is: a tér fénysebességű csavarforgásaihoz kapcsolható az oszcilláló elektromos és mágneses mezők megjelenése. A fotont úgy értelmeztük, hogy a térpont a Compton-sugarú Rc = c/ω henger palástján egyrészt ω  szögsebességű forgást, másrészt c sebességű transzlációt végez Most ezt a képet egészítjük ki avval, hogy a csavarmozgást végző ponthoz rendeljük az egymásra merőleges E és B vektorokat. Ezek a vektorok írják le a fotonnak azt a képességét, hogy kölcsönhatásba kerüljön az elektromos töltésekkel és áramokkal. Itt a hangsúlyt a képesség szóra helyezzük, mert ne feledjük, hogy az elektromágneses mező csak úgy érzékelhető, ha elhelyezünk a térben valamilyen töltést, amire a mező hatni tud. Amíg ott nincs töltés, addig a mező csak fikció, csak matematikai segédeszköz annak leírására, hogy a tér egy kiszemelt pontján milyen lehetséges kölcsönhatással kell számolni. De abban a pillanatban, hogy a töltés megjelent már nem teljesül a kiindulási feltételünk, hiszen töltésmentes térre számoltuk ki az elektromágneses mezőt. A töltés által megfigyelt töltésmentes tér, tehát nem egyéb, mint logikai ellentmondás! A klasszikus elektrodinamika erre azt válaszolhatja, hogy tételezzünk fel egy végtelenül kis töltést, melynek hatása elhanyagolható. Az elektronok kölcsönhatása esetén ez az elhanyagolás azonban nem tehető meg, mert az elektronénál nem létezik kisebb szabad töltés.

Az ellentmondás ezért úgy oldható fel, ha a távoli elektronok kölcsönhatását három szakaszra bontjuk: először a gyorsuló töltés elektromágneses sugárzást bocsát ki, majd a sugárzás az üres térben tovább halad, végül eljut egy másik elektronhoz, ami kölcsönhatásba lép vele és így megváltozik az állapota. A fény, az elektromágneses sugárzás, tehát közvetítő eszköz, ami lehetővé teszi, hogy nagy távolságban lévő elektronok egymással energiát és impulzust közöljenek. Voltaképp ez a hatás felel meg az eltolódási áramnak [2] a Maxwell-egyenletben. Kétféle kölcsönhatást különböztetünk meg, egyrészt erőhatás lép fel a stacionárius pályákon mozgó elektronok között, ekkor beszél a kvantum-elektrodinamika virtuális (nem megfigyelhető) fotonok emissziójáról és abszorpciójáról, másrészt megváltoztathatja az egyik elektron gyorsuló mozgása – vagy stacionárius állapotok közötti energiaugrása – a másik elektron pályáját. Ezt a hatást már a valódi (megfigyelhető) fotonok közvetítik. A virtuális fotonok hatása az elektromágneses mezőre abban tér a klasszikus elektrodinamikai képtől, hogy az E és B vektorok nagysága az átlagérték körül ingadozni fog, ez a vákuumingadozás. Ezt az ingadozást veszi számba a kvantum-elektrodinamika, amikor az elektron anomális mágneses momentumát értelmezi. [3]

De tegyük fel a kérdést, hogy meddig él egy foton, a sugárzás részecskéje? Azt gondolhatjuk, hogy akár milliárd évekig, hisz a legtávolabbi galaxisokból is eljuthat hozzánk a fény. Ha azonban az idő dilatáció jelenségére gondolunk, mely szerint a gyorsan haladó rendszerben lassul az idő, akkor a  t_saját = t_külső (1 – u²/c²)^1/2  szabály alapján bármilyen hosszú, de véges, külső idő esetén az u→c határesetben a sajátidő nulla lesz. Tehát a fénynek nincs is saját belső ideje, sajátrendszerében nézve a képződés pillanatában azonnal eltűnik. Hasonló összefüggés adható meg a fény által megtett útra is, ahol a sajátrendszerben a Lorentz-kontrakció miatt a fény útja is nullára rövidül. Tehát a fény úgy kapcsolja össze a kölcsönhatásba kerülő elektronokat, mintha a téridőben közvetlenül érintkeznének egymással. A kölcsönhatás kontakt jellege magyarázza, hogy miért csak valószínűségi kijelentést tehetünk arról, hogy két kiválasztott elektron, vagy más fermion típusú elemi részecske mikor változtatja meg egymás állapotát: ez akkor következik be, ha a Compton sugarú gömbön értelmezett csavarmozgások fázisa megegyezik, ez a fázis azonban számunkra ismeretlen marad. A folyamat kimenetele így bizonytalan, amit a kvantummechanika az állapotfüggvény valószínűségi amplitúdójával vesz figyelembe. A kvantumelmélet ad magyarázatot arra is, hogy miért látjuk az évmilliárd fényév távolságú galaxisokat is: csak az onnan kibocsátott fotonok száma csökken mire megérkeznek hozzánk a rendkívül hosszú út után, de közben energiájuk állandó marad és így kiválthatják azt a reakciót, ami lehetővé teszi észlelésüket.

Az elektromágnesesség Laplace-egyenletei és a fotonok csavarmozgása

A fotonok csavarmozgása és az elektromágneses mezők Laplace-egyenletének kapcsolatát vizsgáljuk meg konkrét esetekben.  Egy-dimenziós esetben a hullámegyenlet megoldása könnyen áttekinthető, ezért először azt az esetet nézzük, amikor az elektromos- és mágneses mező azonos az xy síkban. Keressük a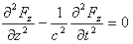

parciális differenciálegyenlet megoldását, ahol az F vektor vonatkozhat akár az elektromos, akár a mágneses mezőre. Vezessük be az ς = z - c.t  változót, melyre

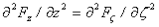 és   

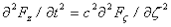
Az egyenlőségből következik, hogy bármely f(z – c.t) függvény kielégíti a hullámegyenletet. Ez viszont azt jelenti, hogy az xy síkban állandó f(z) függvény által leírt elektromos és mágneses mező c sebességgel terjed a z irányban. Az ilyen megoldást nevezzük síkhullámnak. Mivel az f(ς) függvény tetszőlegesen választható, így áttérhetünk a ς’ = -ς/c = t – z/c változóra is, ami megfelel a retardált időnek [4]. Ezért azt mondhatjuk, hogy a t időben z helyen lévő síkhullám azonos a retardált idő origóban lévő értékével: f(z,t) = f(0,t – z/c)). Az így definiált függvény pontosan megfelel a foton csavarmozgásának is, tehát teljes az összhang a klasszikus elektrodinamika és a z irányban c sebességű csavarmozgás között.

A hullámegyenletnek van azonban egy másik, úgy nevezett avanzsált megoldása is:  f(z,t) = f(0,t + z/c)), amelyet úgy is értelmezhetnénk, hogy bizonyos körülmények között a jövőbeli állapot határozná meg a korábbit. Ez viszont ellenkezik az oksági elvvel. Valójában azonban nem sérülhet az oksági elv. Arról van szó, hogy minden jelenséget két irányból közelíthetünk meg: a jelenlegi állapotok ismeretében következtetéseket vonhatunk le arról, hogy milyen lesz a jövőbeli állapot. Ezt teszi a meteorológus, amikor a pillanatnyi légköri adatokból kiszámítja, hogy másnap milyen idő várható. De lehet visszafelé is okoskodni, kiindulva a mai állapotból rekonstruálhatjuk, hogy milyen volt az időjárás egy nappal ezelőtt. Az első esetben pozitív előjelűnek vesszük az időt, a másikban negatívnak. Az elektrodinamika alapegyenletei nem azonosak a Coloumb-kölcsönhatás retardált időre vonatkozó törvényével, nem mondhatunk olyat, hogy előbb volt a töltés és utána jött létre az elektromos mező. A Maxwell-egyenletek nem fejeznek ki időbeli sorrendet az erők és az erők forrása között. Ennek következtében a hullámegyenletek mindkét időirányban egyaránt érvényesek, azaz egyaránt megadhatunk retardált és avanzsált megoldásokat. Ez matematikailag abban fejeződik ki, hogy a hullámegyenletekben kizárólag másodrendű deriváltak léphetnek fel, hiszen ha egy változó szerint kétszer deriválunk, akkor az előjel megmarad.

Nézzünk most egy általánosabb esetet. A gyorsuló ponttöltés nem síkhullámokat, hanem gömbhullámokat bocsát ki, és emiatt gömbszimmetrikus f(r) függvényt keressünk. Írjuk át a Laplace-operátort az r változó segítségével, mely szerint:

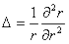
Így a hullámegyenlet:

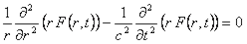
Az egyenlet formailag megegyezik az egydimenziós hullámegyenlettel, csak az f(r,t) = r.F(r,t) jelölésre kell áttérni. Az F(r,t) függvény egyaránt jelölheti az elektromos és mágneses mezőt, vagy a skaláris- és vektorpotenciált, hiszen valamennyit azonos alakú hullámegyenlet határoz meg. A korábbi gondolatmenetet megismételve írhatjuk fel a megoldást, mely szerint r.F(r,t) = f(r – c.t), azaz

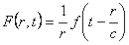
Következésképp a gömbhullám is c sebességgel terjed, de a csillapodás mentes síkhullámmal szemben az amplitúdó a kibocsátó töltés helyétől mért r távolság függvényében csökken. Az r→c.t határesetben a gömbhullám amplitúdója végtelenhez tart. Ebben a határesetben azonban nem érvényes a megoldás, mert abból a feltételből indultunk ki, hogy a vizsgált tartományban a töltés nulla. Ha viszont r = 0, akkor az elektromágneses sugárzást kibocsátó töltés már a vizsgált tértartományban van. Gömbhullám esetén is létezik avanzsált megoldás, ami annak a nézőpontnak felel meg, hogy a t időben épp r sugarú gömbhullámot mikor bocsáthatta ki a gyorsuló elektron. A csavarmodellben akkor kapunk gömbszimmetrikus pályán terjedő fotonokat, ha a haladási irányokhoz egyenlő valószínűségi amplitúdót rendelünk. Az egyenlő valószínűség annak felel meg, hogy amíg a foton nem lép kölcsönhatásba, addig az „irány” fogalmának nincs értelme. A téridő-részecske modell alapelve, hogy az irány, mint a tér egyik koordinátája csak akkor nyer értelmet, ha már létezik valamilyen kölcsönhatás. Az  r = 0 esetre vonatkozó divergenciát elkerüli a csavarmodell, mert az Rc = c/ω  Compton-sugáron belül nem értelmezi a haladási irányt.

 A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"

1. P. Feynman, R.B. Leighton, M. Sands: „Mai fizika”, Műszaki Könyvkiadó, Budapest, 1970
2. Az eltolódási áram: Az elektromos mező időbeli változása az elektromos vezetőn kívül úgy generál mágneses mezőt, mintha ott is áram folyna
3. Lásd a „Screw model for quantum electrodynamics_II” bejegyzést
4. Az r távolságú mozgó töltés r/c idővel később fejti ki hatását a mező fénysebességű terjedése miatt